基于条件判断准则的涡扇发动机限制保护控制器优化设计

白 杰，胡明亮，王 伟，张德生

（1.中国民航大学航空工程学院，天津 300300；2.天津市民用航空器适航与维修重点实验室，天津 300300；3.长安大学机械工程学院，西安 710064）

0 引言

目前，商用涡扇发动机控制系统通常采用最小-最大燃油选择结构来确保飞行员可以在整个飞行包线内无约束地操纵发动机。这种结构确保选择最保守的控制输入，即使热力学参数并没有立即达到危险状态，限制保护控制器也可能被提前激活，导致涡扇发动机响应速度慢于维持安全运行的实际需要，这种保守设计仍然能够满足美国联邦航空局对发动机响应时间的认证要求。然而，在紧急情况下，如发生跑道入侵以及尾翼受损事件时，这种保守的控制器设计方案很可能会影响飞机的飞行安全。如1989年美国联合航空公司232号航班在苏城坠毁以及2001年美国AA587号航班坠毁事件等。

国内外学者对此进行了相关研究，提出了很多降低控制器保守性同时改善发动机响应速度的方法。Litt等在开发增强发动机应急控制响应方法时，试图通过增加设定点控制器的带宽来实现更快的发动机响应，发现涡轮温度限制保护控制器能激活并减缓发动机的响应；Csank等进一步研究发现，即使实际温度远离其极限值，温度极限调节器也开始起作用；Richter等用滑模控制器代替传统线性调节器，有效避免了极限调节器对发动机的过度保护，然而，这种方法需要对发动机控制系统进行重新设计，将在整个飞行包线的验证和发动机控制实施方面带来巨大挑战；薛文鹏等通过改变限制保护控制器的设定值来释放加速限制从而提高加减速性能；陈小磊等通过调整加速计划来提高过渡态性能，但同时增加了极端条件下压气机的喘振风险；Garg等为了在保持当前控制结构的同时降低这种保守性而提出一种新方案，其中发动机极限调节器仅在被限制的变量处于指定范围内且以比规定速率更快的靠近极限值时才处于激活状态，仿真结果表明：这种方法可以在保持必要的安全限制时提高发动机动态响应速度。但其中的边界阈值需要采用传统方法经过一次次试验来得到，耗费了大量人力物力且不具有全局最优性。

本文提出一种基于条件判断准则的涡扇发动机极限调节器设计方案，通过对发动机热力学参数变量的变化趋势来进行主动判断。

1 限制保护控制器的优化设计

1.1 条件判断准则的逻辑设计

当前的航空发动机控制逻辑采用最小-最大控制选择结构，以防止发动机在加减速过程中由于油门指令改变而超过任何安全或操作极限。其整体逻辑框架如图1所示。这种结构本质上是保守的，产生的瞬态响应比需要的慢。为了在保持当前控制结构的同时降低这种保守性更有效地利用现有的安全裕度，提出了一种基于条件判断准则的极限保护控制器的新方案。该方案采用现有的最小-最大架构，但对“限制调节器仅在工作点接近特定限制时才有效”进行修改。

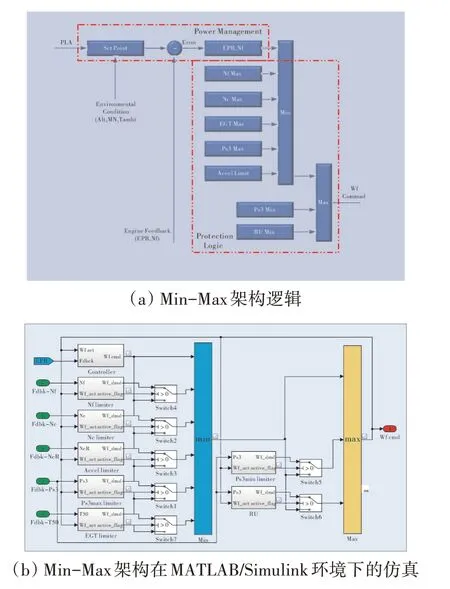
图1 涡扇发动机经典控制系统架构

由于极限调节器的作用是确保不违反规定的极限，如果没有达到极限的机会，则不需要激活。因此，限制保护控制器在最小-最大选择方案中激活的操作区域可以被定义为：条件1，要被限制的变量“接近”其极限值；条件2，其当前速率使得它将在某个时间段内达到极限，而没有其他变化。为了使极限调节器处于激活状态，条件1、2都必须为逻辑真。

对于（发动机排气温度）、（风扇转速）、（高压转子转速）、（高压压气机最大出口静压）等最大极限保护控制器参数，其最终目的就是为了保持≤；≤；≤；≤。因此，根据条件1、2可得最大极限调节器的条件判断准则

式中：N为涡扇发动机某热力学变量在时刻对应的数值；为其设定的安全极限值；为其在安全极限范围内所占有的比例；为热力学参数在某一时刻的数值；Δ则为控制系统的采样时间；为参数以当前的变化率到达系统设定的极限值所需要的采样时间Δ的倍数；为系统设定的激活边界阈值；为系统给定的变化率激活边界阈值。

当≥且≤时，则认为此热力学参数极其接近系统设定的极限值而且变化剧烈。如果按当前的变化率则在·Δ内变量要超越系统极限值，使发动机处于危险状况。此时应激活极限调节器，参与控制系统架构Min-Max的逻辑选择。决定限制保护控制器是否掌握控制系统的控制权，其逻辑判断准则见表1。

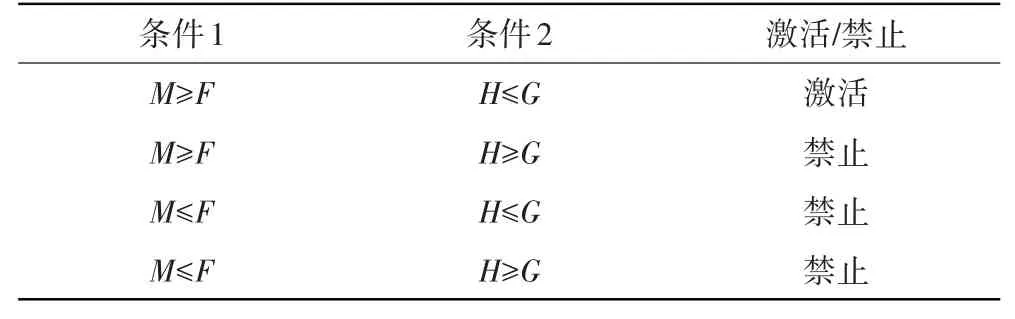
表1 限制保护器激活判断逻辑

对于（高压压气机最小出口静压）等最小极限保护控制器参数，其目的是保持≥。其条件判断准则为

上述最大极限保护控制器和最小极限保护控制器的各条件判断准则在MATLAB/Simulink环境中的仿真如图2所示。

图2 条件判断准则在MATLAB/Simulink中仿真

涡扇发动机每个限制保护控制器条件判断准则模块中的“条件1”和“条件2”的逻辑框架在MATLAB/Simulink中的仿真如图3所示。

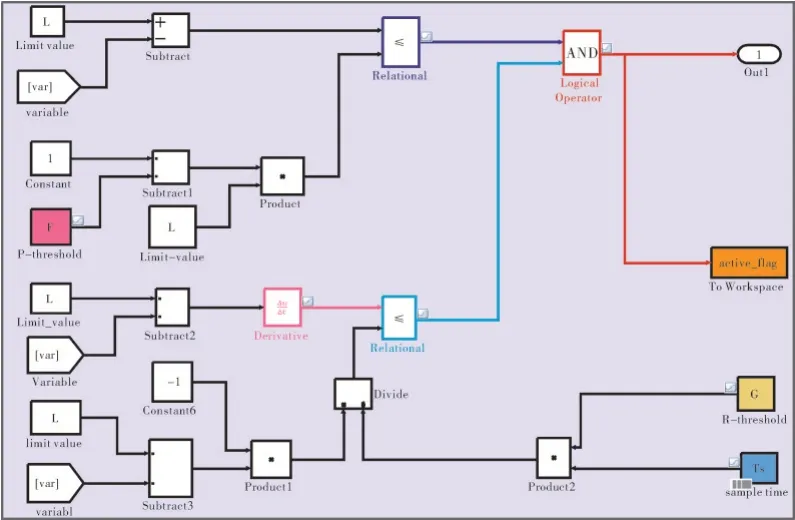
图3 条件1与条件2逻辑框架在MATLAB/Simulink中仿真

1.2 基于粒子群算法对边界阈值寻优

由第1.1节的条件判断准则分析可知，限制保护控制器有效作用的关键在于选择边界阈值和的数值大小。如果阈值选择过大，则当涡扇发动机某个热力学参数超过其给定的极限值时，限制保护控制器无法及时有效地对发动机进行保护，有可能导致发动机损坏甚至导致灾难性后果；反之，边界阈值选择过小，当发动机没有出现到达极限值的紧急情况时，限制保护控制器有可能被提前激活，导致控制系统的动态响应速度减缓，从慢车状态到达起飞状态的过渡时间超过《航空发动机适航审定》CCAR 33.28和CCAR 33.75条款中规定的5 s响应时间。

基于上述分析，本文采用粒子群优化算法（Particle Swarm Optimization，PSO）来寻找优化边界阈值和。PSO算法需调整的参数较少，结构简单，易于工程实现；而且没有交叉和变异运算，搜索速度很快，非常适合工程领域寻优。

基于PSO算法寻找优化条件判断准则边界阈值的计算流程如图4所示。首先需要对粒子群进行初始化，产生随机粒子，然后将随机粒子的数值依次赋予限制保护控制器中的和2个参数。针对该参数使Simulink动态模型运转，得到此时的适应度函数值，将该值作为输出，输入判断模块，如果不满足终止条件，则对粒子群进行再次更新，再次赋予限制保护控制器的2个参数进行运算。如果满足终止条件，则退出循环输出最优值。

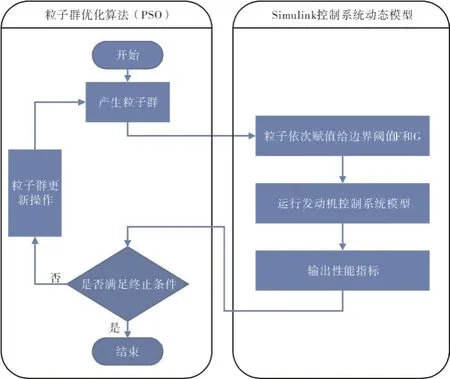
图4 粒子群算法优化边界阈值计算流程

目标函数越小代表优化效果越好

式中：为目前所处时间；为限制保护控制器期望值；表示此刻变量反馈值。

本文以文献[15]中的航空发动机控制系统仿真平台作为研究对象。当Accel限制保护控制器中的极限值设定为1510时，采用双变量参数寻优，控制系统采样时间设定为0.015 s；种群数量选取100；惯性因子选择0.6；学习因子和设置为2；在SLS（海平面飞行条件下海拔高度为0、=0）条件下进行仿真，其粒子群算法运行的适应值变化和自变量最优值如图5、6所示。

图5 适应值变化

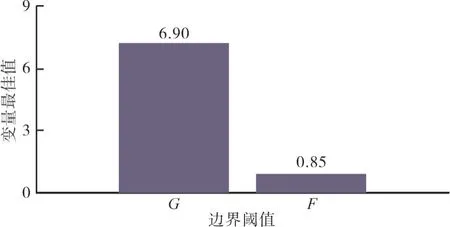
图6 边界阈值最优解

基于上述优化流程，依次得到、、、等最大极限保护控制器和等最小极限保护控制器的边界阈值，见表2。

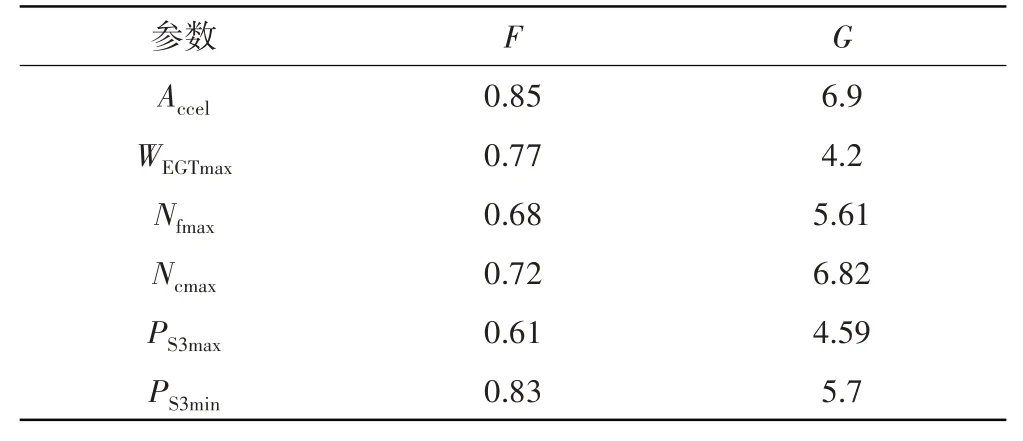
表2 限制保护器边界阈值优化数值

2 仿真验证

为了对比原始控制器和改进控制器在动态响应速度方面的优劣，将表2中的边界阈值代入仿真平台中，在SLS条件下（海平面飞行环境海拔高度为0、=0）从慢车状态短时间内加速到起飞状态，其中油门操纵杆在0.1 s内从40°拉伸到80°。原始控制器和改进控制器的仿真结果如图7所示。从图7（a）中可见，到达95%最大推力，传统线性控制器的响应时间为4.7 s，而基于条件判断准则的限制保护控制器的响应时间则为3.8 s，缩短了近20%，控制系统的保守性得到了有效降低。从图7（k）中可见，传统线性控制系统其保护器（包括过渡态限制器和稳态限制保护器）激活时间总计为3.86 s，而改进后的限制保护器激活时间只有1.97 s，约缩短了48%。在任何给定的时间段内只有1个限制保护控制器处于激活状态，这是由于最小-最大体系结构所决定的。从图7（c）中可见，采用线性调节器的涡扇发动机在加速过程中是以保守方式运行的（高压压气机喘振裕度距离最小极限值还有一定距离），使用改进后的限制保护器能够降低这种保守性，使压气机喘振裕度曲线沿着极限值运行且始终大于给定的极限值。从图7（e）、（f）、（g）、（h）、（j）中也可见，改进后的限制调节器能够有效地保护发动机各输出变量在极限值范围内，证明了改进后的限制保护控制器的有效性以及优越性。

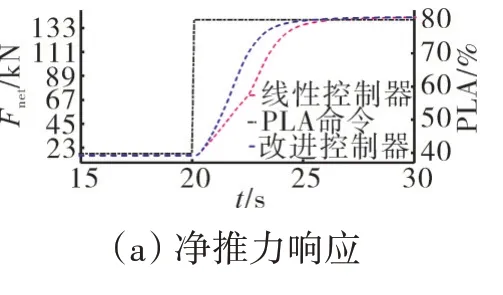
图7 线性控制器和改进控制器响应曲线

除了在SLS（海平面飞行环境海拔高度为0、=0）条件下进行仿真验证，还在高空飞行条件下（海拔高度为914 m，=0.6）进行了数值模拟仿真，仿真结果与图7中各热力学变量的时间响应曲线非常相似。由于结果的相似性，本文不再赘述。

3 结束语

本文介绍了一种在传统发动机控制系统最小-最大选择结构中基于条件判断准则的极限保护控制器概念。规定只有被限制的变量“接近”其极限值，且以当前速率使得其将在某个时间段内达到极限，而没有其他变化时才激活与之对应的极限保护控制器。其中，条件判断模块中的边界阈值采用粒子群智能进化算法在合理范围内搜索出最优解，从而设定合理可靠的阈值。仿真结果表明：通过正确选择极限调节器边界阈值的参数，能够降低整个涡扇发动机控制系统的保守性，有效提高发动机推力的响应速度，同时保持所有必要的安全极限，且该优化设计方法逻辑结构较为简单，对原有控制系统的结构改动较小，优化效果良好，具有非常强的工程实际意义。