凹形多面体离散单元的水平集函数接触算法

王嗣强, 薛一桢, Michael Zhuravkov, 季顺迎*,3

(1.大连理工大学 工业装备结构分析国家重点实验室,大连 116024；2.白俄罗斯国立大学 理论与应用力学系,白俄罗斯明斯克 220030；3.大连理工大学 大连理工大学白俄罗斯国立大学联合学院,大连 116024)

1 引 言

离散单元法DEM(Discrete Element Method)是分析颗粒材料宏-细观力学特性的有效数值方法[1-3]。该方法最初采用球体单元表示固体颗粒，具有单点接触和搜索简单等特点[4,5]。然而，日常生活及实际生产中固体颗粒普遍有凹凸表面特性，并且凹凸形态显著影响颗粒材料的力学响应[6,7]。为合理地描述非规则颗粒形态，基于二次曲面函数的椭球体模型、基于二次曲面扩展的超椭球模型、基于几何拓扑的多面体模型以及基于球体包络的光滑多面体模型等不同的离散元方法不断完善[8-10]。受数学函数模型及单元接触算法的限制，上述离散元方法通常用于计算凸形颗粒间的单个接触点，并且考虑局部收敛的数值迭代算法难以直接计算凹形颗粒间的多个接触点及作用力[11]。

目前，凹形颗粒材料离散元方法主要包括组合单元模型和单个凹形颗粒模型。其中，组合单元模型最初将不同数目的球体单元以一定的重叠量进行任意组合，进而构造凹形颗粒形态。该方法具有较好的扩展性，可将不同长宽比、表面尖锐度、空间取向的圆柱体、球柱体和超椭球等多种凸形颗粒进行组合[12-14]。同时，组合单元间多个接触点的搜索判断可简化为基本凸形单元间单个接触点的数值计算，这显著降低了凹形颗粒间多接触点搜索的复杂性。然而，组合单元模型本质上是一种近似构造方法，其与真实颗粒形状存在一定的差异。同时，单颗粒层面引入的形状误差会影响凹形颗粒材料的运动行为[15]。此外，单个凹形颗粒模型逐步发展，包括心形颗粒、傅里叶级数、随机场理论、非均匀有理样条、能量守恒理论和球谐函数模型等[16-20]。不同的构造方法及接触理论在算法灵活性、数值稳定性和计算效率等方面具有独特的优势，同时也有一定的不足。因此，发展更加稳定和高效的凹形颗粒材料离散元方法仍是当前数值模拟的难点问题。

水平集方法是一种计算界面运动和追踪断裂演化路径的有效数值方法，广泛地应用于三维建模、图像识别、界面分割和断裂表征等不同领域[21-23]。由于界面分割及识别中具有尖锐棱角、平面和内部空腔等复杂几何特征，水平集方法可对计算机断层扫描得到的真实颗粒形态进行精确几何重构和表征[24,25]。Kawamoto等[26]首次采用水平集方法将复杂颗粒形态的尺寸、数目、排列方式、长宽比和表面尖锐度等特征参数输入至离散元模拟中，并且实现了任意形态颗粒材料的动力特性分析。水平集方法和离散单元法的结合不仅能够计算宏观尺度上颗粒材料整体流动、压缩变形及倒塌破坏等动力行为，还能够从细观尺度上分析单个颗粒的运动、旋转及应力情况[27-29]。同时，水平集方法可对任意形态颗粒材料的剪切带形成、演化过程和内部力链结构进行准确模拟[30,31]。因此，水平集方法为凹形多面体单元间多接触点的搜索计算提供了很好的研究思路。

本文针对凹形单元间多接触点的搜索计算问题，发展了适用于凸形和凹形多面体单元的水平集函数接触算法。通过点-三角形单元距离计算方法和奇-偶数判定方法对多面体单元进行水平集函数重构，同时将所有零水平集点代入邻居单元的空间水平集函数中进行三线性插值计算，以实现凸形或凹形多面体间单个或多个接触点的准确计算。在此基础上，对球体和凹形多面体颗粒材料的下落堆积及颗粒柱倒塌过程进行离散元模拟，分析不同多面体形态对堆积分数和休止角的影响规律。

2 多面体单元的水平集函数重构

采用多面体模型构造球体以及具有内部空腔和悬臂特征的凹形颗粒，通过点-三角形单元距离计算方法和奇-偶数判定方法对多面体单元进行水平集函数重构，进而形成零水平集函数和空间水平集函数。

2.1 多面体单元的几何构造

多面体模型是一种数学意义上描述非规则颗粒形态的普遍方法，其由若干个平面、棱边和角点组成。该模型通过表面网格包络对颗粒形态进行表征，不仅克服了椭球体和超二次曲面在函数构造方面的几何对称性和严格凸形限制，还有效避免了球谐函数和非均匀有理样条仅适用于表面光滑颗粒的应用局限性。当平面、棱边和角点的数目足够多时，该方法理论上可构造任意形态的固体单元，如图1所示。

2.2 多面体单元的水平集函数重构

针对多面体单元的空间水平集函数，空间点在单元内外均以等间距方式生成。首先，判断空间点是位于单元内部或外部。本文采用奇-偶数判定方法，即计算以空间点为端点的射线与单元表面的交点个数。当总数为奇数，则该点在单元内，空间点用蓝色表示且Dp=-1；当总数为偶数，则该点在单元外，空间点用红色表示且Dp=1。图2(b)显示了由红色和蓝色空间点组成的空间水平集函数，并且蓝色空间点组成的几何形状基本与颗粒形状相同。其次，通过遍历所有的三角形单元，并采用点-三角形单元距离计算方法可得到空间点与单元表面的最短距离Dmin。每个空间点P的水平集函数值可表示为Dp=Dp·Dmin，不同形态颗粒的空间水平集函数如图2(c)所示。空间点的不同颜色表示该点与单元表面的不同距离，并且空间水平集点的数目仅会影响多面体单元在水平集函数重构时的运行时间和内存消耗。因此，本文多面体单元的空间水平集点数目约为1×106个。

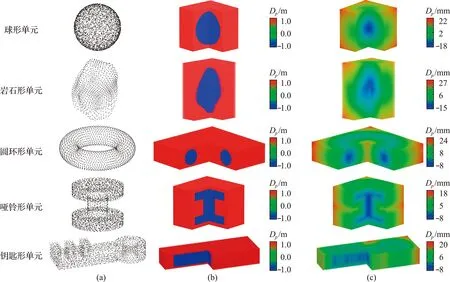
图2 任意形态颗粒的零水平集函数和空间水平集函数

3 基于水平集函数的接触算法

任意形态多面体单元间的接触判断可转化为零水平集函数与空间水平集函数间的求解问题，通过三线性插值方法计算单元间的多个接触点，并采用非线性黏-弹性接触力模型计算单元间的作用力和力矩。

3.1 基于水平集函数的接触点计算方法

在全局坐标系下，两个邻居单元分别表示为i和j。由于空间水平集函数是由1×106个空间点组成，并且点与点在方向x,y和z上的间距相同，即dx=dy=dz=d0。这有利于在单元i的空间水平集函数中快速寻找该零水平集点周围的8个空间点，如图3所示。Pj表示单元j的零水平集点，ψ000表示在单元i的空间水平集函数中点P000的函数值。当零水平集点周围存在8个空间点时，则这个点可能为单元间接触点。当所有零水平集点均位于单元j外部时，单元i和j不发生接触。

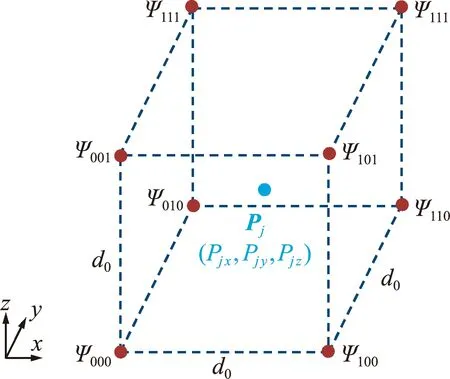
图3 一个零水平集点周围的8个空间点

零水平集点Pj在8个空间点的坐标为

(1)

式中Pj x,Pj y和Pj z为点Pj的坐标位置；Px,000,Py,000和Pz,000为点P000的坐标位置。

采用三线性插值方法计算点Pj在单元i的水平集函数值Ψ(Pj)，可表示为[26]

[(1-b)(1-y)+by][(1-c)(1-z)+cz]

(2)

此外，点Pj的水平集函数梯度Ψ(Pj)可表示为[26]

by][(1-c)(1-z)+cz]

(3)

(2b-1)[(1-c)(1-z)+cz]

(4)

[(1-b)(1-y)+by](2c-1)

(5)

如果DP j<0，则点Pj在单元i内部，并且两个单元发生接触。单元间的接触法向n可表示为n=Ψ(Pj)，重叠量δn可表示为δn=Ψ(Pj)n。将满足DP j<0的全部零水平集点进行存储并作为凹形单元间的多个接触点，同时采用非线性黏-弹性接触力模型进而准确计算多面体单元间的作用力。

3.2 非线性黏-弹性接触力模型

在离散元模拟中，多面体单元的总接触力F和力矩M可表示为

F=Fn+Ft,M=Mn+Mt+Mr

(6,7)

(8)

(9)

(10)

(11)

4 多面体离散元方法的算例验证

为验证水平集函数接触算法的有效性，分别对球形和凹形多面体颗粒材料的下落堆积和倒塌过程进行离散元模拟，并分析颗粒形状对堆积密度和休止角的影响规律。

4.1 多面体颗粒材料的下落堆积过程

采用多面体模型构造球形单元、岩石形单元、圆环形单元、哑铃形单元和钥匙形单元，如图1所示。通过水平集函数重构方法将5种多面体单元表征为零水平集函数和空间水平集函数，如图2所示。多面体单元的等效球体直径设定为4 cm，数值模拟参数列入表1。

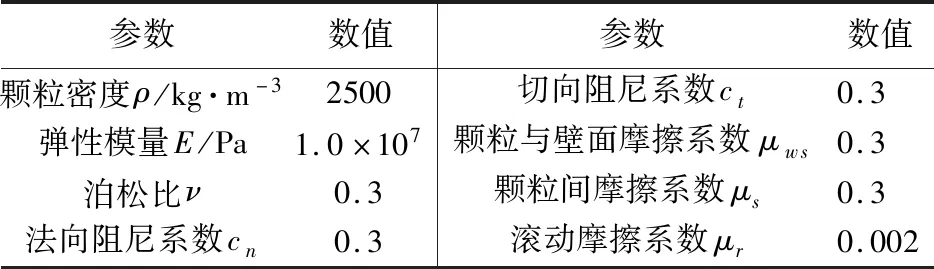
表1 多面体单元的离散元参数

长方体容器的长、宽和高分别为35 cm，35 cm和150 cm。总计1000个多面体颗粒以随机位置和方位取向在长方体容器中生成，并进行重力下落和堆积，如图4所示。颗粒颜色表示颗粒的初始生成高度，并且蓝色至红色的渐变过程表示颗粒具有不同的竖向高度。最终，不同形态颗粒在长方体容器中形成稳定的颗粒床，如图5所示。可以看出，球体和岩石形颗粒具有较低的堆积高度，而圆环形、哑铃形和钥匙形颗粒具有较高的堆积高度。同时，进一步统计了不同形状颗粒的体积分数，如 图6 所示。球体和岩石形颗粒的体积分数相对较高，分别为 0.616 和0.619。具有内部空腔或悬臂特征的圆环形、哑铃形和钥匙形颗粒的体积分数较低。这是因为颗粒内部的空腔和悬臂结构使得颗粒从紧密的面接触转变为局部的多点接触，从而产生更多的内部空隙。此外，岩石形颗粒的体积分数高于球形颗粒，这是由于岩石形颗粒具有较大的接触面积，紧密的面接触使得颗粒材料内部具有更少的空隙。

图4 凸形和凹形多面体颗粒的堆积过程

图5 凸形和凹形多面体颗粒的稳定堆积状态

图6 颗粒形状对颗粒材料体积分数的影响

将球形颗粒、岩石形颗粒、圆环形颗粒、哑铃形颗粒和钥匙形颗粒进行混合堆积，以验证水平集算法的可靠性。图7为5种颗粒形态混合后形成的稳定颗粒床，并计算下落堆积过程中颗粒材料的能量转变情况，如图8所示。在最终时刻，颗粒动能为0，而势能和总能量保持恒定。因此，水平集函数接触算法对模拟球形和凹形多面体单元的堆积过程具有较好的数值稳定性。

图7 不同形态颗粒的混合堆积

图8 在混合颗粒堆积中不同能量的转变关系

4.2 颗粒柱倒塌的离散元模拟

为进一步验证水平集接触算法对凹形多面体颗粒材料流动性能模拟的准确性，采用离散元方法模拟5种形态颗粒柱的倒塌过程。图9为球形、岩石形、圆环形、哑铃形和钥匙形颗粒柱倒塌后形成的堆积图案。可以看出，球形、岩石形和圆环形颗粒更容易滑动和滚动，并且具有较低的堆积高度。哑铃形和钥匙形颗粒具有复杂的悬臂结构，这使得颗粒在倒塌过程中形成团簇和互锁结构，并阻碍颗粒向右侧的流动过程。因此，具有悬臂结构的颗粒材料具有较低的流动性和较高的堆积高度。

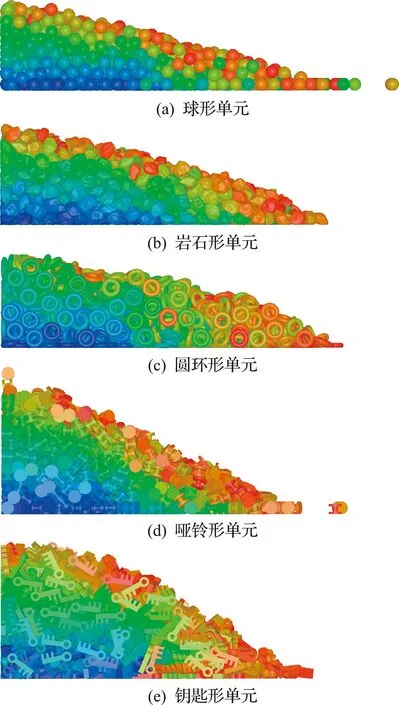
图9 颗粒形状对颗粒柱倒塌后堆积状态的影响

将不同形态颗粒材料的休止角进行统计，如 图10 所示。球形颗粒的休止角约为15.9°，这基本对应于颗粒间的摩擦系数0.3。球形和圆环形颗粒具有更光滑的表面，这有利于颗粒间相对滑动，进而降低了颗粒材料的稳定性且产生较小的休止角。岩石形颗粒具有凹凸表面特性，容易形成面接触并组成较低空隙率的颗粒材料。紧密的接触模式阻碍了颗粒柱的流动过程，进而产生比球形和圆环形颗粒材料更大的休止角。哑铃形和钥匙形颗粒具有复杂的悬臂结构，这种复杂几何特性使得颗粒更容易形成团簇结构和互锁效应，并且在流动过程中容易形成拱形结构并进一步阻碍颗粒运动。因此，哑铃形和钥匙形颗粒具有最大的休止角。

图10 颗粒形状对颗粒材料休止角的影响

此外，为描述颗粒柱倒塌的运动距离，本文引入无量纲距离D*，

D*=(Df-D0)/H0

(12)

式中Df为倒塌过程中颗粒柱的宽度,D0和H0分别为颗粒柱的初始宽度和高度。

由于不同形态颗粒柱的倒塌时间不同，采用归一化时间t*描述颗粒柱的倒塌时间，可表示为

t*=t/tm

(13)

式中t为倒塌过程的实际时间,tm为颗粒柱开始倒塌至稳定堆积的总时间。

图11为不同形态颗粒柱的无量纲运动距离随归一化时间的变化关系。可以发现，随着颗粒柱开始倒塌，不同形态颗粒柱的运动距离呈先增加后保持恒定的趋势。同时，颗粒形状显著影响颗粒材料的休止角。表面光滑的球形颗粒具有最远的运动距离，而具有内部空腔和悬臂结构的钥匙形颗粒具有最近的运动距离。一般而言，随着颗粒形状复杂度的增加，颗粒材料具有更强的互锁效应和更多的团簇结构，这阻碍了颗粒间的相对运动并且降低了颗粒材料的流动性。

图11 不同形态颗粒柱的无量纲运动距离随归一化时间的变化关系

5 结 论

本文基于多面体模型构造球形和凹形颗粒，发展了基于水平集函数的离散元接触算法。该算法通过点-三角形单元距离计算方法和奇-偶数判定方法对凸形和凹形多面体单元进行水平集函数重构，形成由零水平集点和空间水平集点表征的颗粒形态。同时，将全部零水平集点代入邻居单元的空间水平集函数中，采用三线性插值方法计算单元间的单个或多个接触点，从而实现凸形和凹形多面体单元间接触力的有效计算。在此基础上，对球形、岩石形、圆环形、哑铃形和钥匙形颗粒材料的下落堆积和倒塌过程进行离散元模拟。计算结果表明，颗粒形态显著影响颗粒材料的体积分数和休止角。表面光滑的球形和岩石形颗粒具有较高的体积分数和较低的休止角，而具有内部空腔和悬臂结构的圆环形、哑铃形和钥匙形颗粒具有较低的体积分数和较高的休止角。随着多面体单元的凹凸表面特性变得更加显著且内部空腔和悬臂结构变得更加复杂，非规则颗粒材料的空隙率增加，流动性降低。