台风灾害下基于V2G 的城市配电网弹性提升策略
杨祺铭,李更丰,别朝红,邬嘉雨,季陈林,刘达夫
(1. 电力设备电气绝缘国家重点实验室(西安交通大学),陕西省西安市 710049;2. 四川大学电气工程学院,四川省成都市 610065;3. 国网江苏省电力有限公司无锡供电公司,江苏省无锡市 214061)
0 引言
近年来,频发的台风灾害给沿海城市电网运行带来极大挑战,严重危害到城市能源安全和社会发展[1]。提升城市在灾害中快速应对及恢复的能力已被列入“十四五”规划中[2]。配电网作为城市能源系统的重要组成部分,必须具有抵御台风等极端灾害的能力,以保证能源安全,尽量减少供电中断对经济社会造成的巨大损失。因此,有必要研究应对台风等极端灾害的城市配电网弹性提升策略。
国内外学者针对城市配电网弹性提升策略已经开展了大量研究。城市配电网弹性可定义为针对小概率高损失极端事件的预防、对抗及快速恢复能力[3]。文献[4-5]根据灾害历史数据对配电网系统进行弹性评估,分别从脆弱性分析、故障概率曲线以及弹性评估指标体系3 个方面进行研究。文献[6-7]考虑灾害破坏最恶劣场景,分别采用分布式资源、天然气网备用资源以及加固重要线路的方法,提出城市配电网预防与抵御极端事件的措施。文献[8-11]通过拓扑优化、人工检修、增设远动开关等方法,提高了城市配电网快速恢复能力。从已有研究来看,台风等极端灾害场景下,系统自身可提供的电能资源有限,制约了弹性提升效果。
同时,也有研究提供了一些新型的弹性提升手段,以帮助城市配电网实现快速供电恢复。文献[12-14]引入能够更好地控制系统电压与无功功率的智能软开关,以减小配电网故障对整个系统带来的负面影响。文献[15-16]提出一种移动储能调度模型,确定灾后恢复过程中的最优路径。文献[17]根据工程实际需要,将移动电源车细分为移动储能车、应急发电车(mobile emergency generator,MEG)和移动电池车3 类,并确定其供电恢复范围。移动电能资源因其可移动的空间特性,可以在灾害发生后快速将电能转移到系统中的缺电区域,解决了系统内电能资源有限的问题,但过高的经济成本限制了其在配电网弹性提升中的工程实际应用。
电动汽车(electric vehicle,EV)作为城市中广泛存在的分布式移动储能单元,被逐渐应用于配电网弹性提升研究中。在灾后,EV 以车辆并网(vehicle to grid,V2G)的形式参与配电网供电恢复,从而可以充分利用有限的电能资源并降低经济成本。文献[18]对EV 提升配电网弹性的合理模式及可能性进行了总结,为后续研究提供了参考方向。文献[19]构建了EV 锂电池梯级利用模型,以提高系统弹性和经济性。文献[20]提出一种基于EV 换电模式的弹性提升策略。然而,现有研究较少关注EV 用户的自主选择行为及由此而导致的时空分布特性。因此,有必要计及EV 出行特征,考虑用户在灾害环境下选择行为的改变,研究基于V2G 的城市配电网弹性提升策略。
综上所述,在高比例EV 接入的配电网中,本文针对台风灾害造成的部分节点电力供应不足的问题,考虑灾后EV 参与供电恢复,提出了一种基于V2G 的城市配电网弹性提升策略。本文主要贡献包括:1)考虑EV 用户在灾害过程中的行为特征,提出了适用于灾害前期场景的EV 调度策略与V2G 用户激励机制;2)提出了弹性背景下考虑V2G 反向输电的具备较好经济性的供电恢复方案,为弹性配电网供电恢复提供了新思路;3)运用多种弹性评估指标,对比MEG 与V2G 在弹性供电恢复中的作用,分析了V2G 参与供电恢复的优劣性。
1 灾害场景生成与灾害前期EV 调度模型
1.1 灾害下配电网的故障场景生成
以台风为例,生成极端灾害下的配电网故障场景。首先,量化线路和杆塔受到风的应力作用与故障率的关系,以体现台风对配电网元件的影响;其次,采用非序贯蒙特卡洛模拟法采样配电网中每条线路的状态;最后,根据N-K原则对生成的故障场景进行筛选,其中N为线路总数,K为多重故障的阶数。具体的台风场景下的故障场景生成过程详见附录A。
1.2 灾害前期的EV 调度模型
灾害前期是指台风灾害强度提升到开始对城市配电网产生破坏的时间点之前。计及EV 的出行特征,对区域路网及电网进行建模后,基于该模型采用出行链理论描述灾害前期EV 用户的调度行为,并且记录调度周期内EV 的时空分布状态及剩余电量[21-22]。该模型中,出行意愿部分反映了EV 用户在灾害过程中的出行选择行为。
1)路网建模

式中:V为简化图中路网节点的集合;E为图中各节点间连通关系的集合;G为路网连边集合。
生成矩阵D(G)来记录各节点间的直接连接距离,若不是直接连接,则为无解(inf)。接着,基于D(G),采用Floyd 最短路径算法可得出任意两点间的最短路径行驶方案。
2)路网与电网耦合建模
可以将两网耦合关系等效为路网、电网两层之间是否有层间节点连接。


式中:ζ为路网和电网间节点的连边集合;Eαβ为路网与电网构成的耦合边集合;Vα为路网节点集合;Vβ为电网节点集合;为路网的第i个节点;为电网的第j个节点;α为表示路网、电网之间是否有层间节点连接的0-1 变量,若α=1,则两网间路网节点i与电网节点j存在耦合关系。从能量传输上来看,两网耦合关系可以等效成路网上的站点从对应电网中的节点获取电能。
3)基于出行需求的出行链建模
将整个路网构成的区域分为3 种功能区域,即居民区(R)、工作区(W)、休闲区(L),并分别生成对应路网节点集合R、W和L。将出行链分为简单链和复杂链,分别经过2 个和3 个节点(包括终点)。

式中:TC为出行链中一段行程的状态变量集合,包含起点(不一定是出发地)L0、终点(不一定是目的地)Lf、行驶路径P0f、出发时间T0、到达时间Tf、行驶时长t0f、停驻时长Ts。
台风灾害会一定程度地影响EV 用户的出行行为。由文献[23]可知,在台风灾害下早高峰时段的道路拥堵情况较为明显,平均速度约下降29.4%。同时,道路拥堵情况以及用户对于灾害的恐慌还会降低用户的出行意愿。为体现灾害对用户出行意愿的影响,本文引入出行比例系数α2来量化EV 用户群体的总出行意愿变化[24]。

式中:Nroad为出行的EV 数量;NEV为EV 总数。
第l段路程的行驶时长t0f,l、到达时间Tf,l和下一段路程出发时间T0,l+1表示如下:

式中:v为EV 行驶的平均速度;dl为第l段路程的长度。
根据美国国家公路交通安全与管理局(NHTS)的EV 调查数据[25],居民每天首次和末次出行符合一定的正态分布N(μ,σ2),其中μ为均值,σ2为方差。
首次出行出发时间Tfirst(t)为:

最后一次出行出发时间Tfinal(t)为:

4)EV 实时状态建模

式中:H为在时刻t每辆EV 实时状态信息的集合,包含该时刻每辆车的剩余电量Srem,t、行驶状态wt和离所在位置最近的V2G 交互站编号Pt。
2 V2G 用户参与供电恢复引导补偿机制
为引导EV 用户在台风灾害下参与供电恢复,本章考虑EV 用户灾后的响应选择行为,提出包含避难阶段和响应阶段的供电恢复引导补偿机制,如图1 所示。在避难阶段,停驻在V2G 站点的EV 停止充电,行驶中的EV 寻找最近的V2G 站点进行避难;在响应阶段,V2G 站点里的EV 在激励机制的引导下,参与供电恢复。
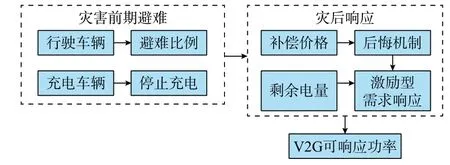
图1 灾害前期避难调度与灾后激励响应机制Fig.1 Evacuation scheduling in the early stage of disaster and incentive response mechanism after disaster
需要指出的是,该台风灾害场景并未达到毁灭性的程度,也不会造成严重的电力及交通故障情况。所提供电恢复引导机制在台风灾害发生时及灾后能够保证V2G 站点内EV 用户人身安全,且参与供电恢复的EV 能够获得一定的经济收益。
2.1 避难阶段
当灾害开始对电力系统造成破坏时,基于用户出行需求的EV 自由调度停止,此时即为避难阶段,需确定该时刻t的EV 空间分布及行驶状态。避难阶段中,原本停在V2G 交互站充电的EV 将停止充电,原本在路上行驶的EV 将被引导前往就近的V2G 交互站。
引导避难的过程是以安全性为主要导向原则的。严重灾难面前,保证安全是人潜意识下的应激反应,V2G 站点具有良好的避难效果,对在路上行驶的EV 用户具有较强的吸引力,可以通过舆论宣传引导在路上行驶且靠近站点的EV 前往并参与V2G 反向输电。

式中:Nstation为在V2G 站点停驻的EV 数量;σ1为响应引导并前往V2G 站点避难的EV 用户比例;Nre为实际响应并前往V2G 站点避难的车辆数。
参与V2G 反向输电的EV 用户能否有足够的电量持续为电网提供支撑十分关键。因此,需要对站内的EV 进行筛选:

式中:P为V2G 站点额定放电功率;TRescue为供电恢复抢修时间,从停电到抢修恢复的时间由两部分组成,即到达现场时间(城区约为45 min、偏远地区约为2 h)和现场抢修时间,根据故障情况,现场平均抢修时间为3~5 h[26],故本文中取TRescue为4 h。
2.2 响应阶段
当灾害不再对电力系统造成破坏时,可引导用户参与电力系统的灾后恢复过程,此时即为响应阶段。用户响应的过程是以经济利益为主要导向原则的。基于需求响应的激励机制,可以促使在站内的EV 用户参与V2G 反向输电,该过程中需对激励的程度和用户响应行为之间的关系以及用户响应的不确定性进行建模。
本文采用消费者心理学理论[27-28]来描述签订合同过程中,用户的放电响应行为与V2G 服务聚合商的激励价格之间的关系。用户参与需求响应的响应行为存在一定的感觉阈值:只有当激励高于阈值下限时,用户才愿意与V2G 服务聚合商签订合同,参与需求响应。在感觉阈值内,价格激励越高,用户的放电响应概率越大,能够参与需求响应的总V2G 容量就越大。

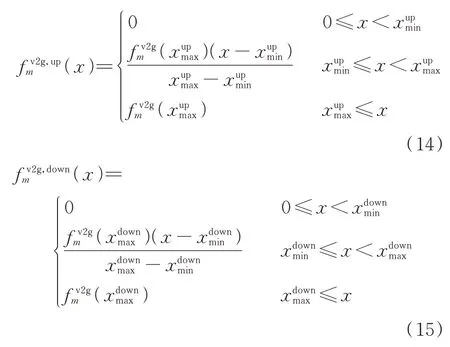
本文中主要考虑台风场景,因此,实际计算时各参数后缀应带“2”。

式中:U[·]表示均匀分布;f͂v2gm(x)为用户m的放电响应率。
当经济激励水平为x时,放电响应波动程度如下所示:
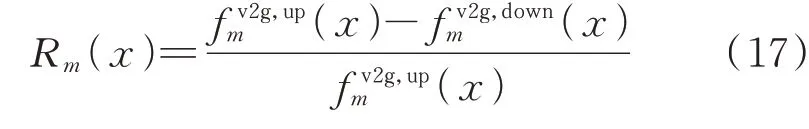
式中:Rm(x)为用户m的响应波动程度。
节点b处对应激励水平为xm的Nb个EV 用户的实际V2G 响应出力记为:

式中:Nre1b为经第1 阶段到达节点b充电且剩余电量能够满足持续放电需求的EV 数量;Pv2g为单辆EV的反向充电功率;(xm)为用户m在激励水平为xm时的放电响应率。
由此,可确定节点b处有意向参与配电网供电恢复的EV 数量N为:
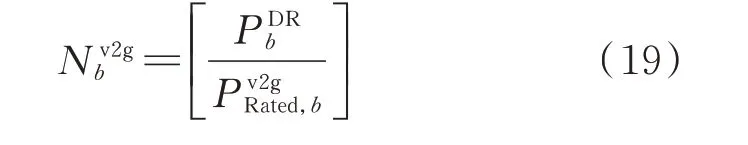
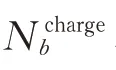
V2G 服务聚合商补偿给用户的成本Cv2g包含电量成本和单次响应成本,即
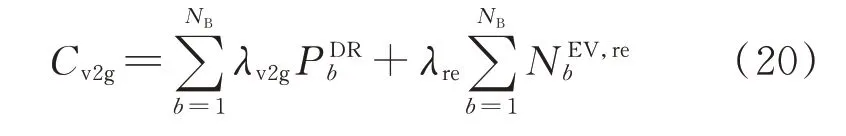
式中:NB为节点总数;λv2g和λre分别为单位响应功率的补偿价格和单次响应行为的补偿价格。
3 考虑V2G 反向输电和配电网重构的经济性灾后恢复模型
3.1 考虑二阶锥约束的配电网重构交流最优潮流模型
本文所提的灾后恢复模型是指考虑二阶锥约束的配电网重构交流最优潮流(alternating current optimal power flow,ACOPF)模型。其中,灾后是指台风灾害强度下降到对城市配电网不再有破坏能力的时间点之后,因此,灾后阶段配电网拓扑不再改变。统计各V2G 站点内的EV 数量,并计算各V2G站点可提供的出力。有V2G 站点的路网节点上V2G 装置分别连接对应的配电网节点。为简化模型,只考虑重构以后配电网功率平衡,参与反向输电的各V2G 交互站点按耗电功率为负的负荷处理。
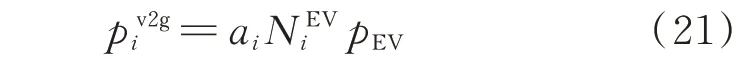
式中:pv2gi为配电网节点i上V2G 装置的反向输电功率;NEVi为配电网节点i上接入的EV 数;pEV为单辆EV 反向充电的额定功率;ai为表示配电网节点i是否有V2G 站点接入的0-1 变量,配电网节点i有V2G 站点接入时ai=1,并且站点会参与反向输电进行供电恢复,否则ai=0。因单个交互站内充电桩数量有限,需要设置一定的出力上限加以限制。
因此,灾后供电恢复即可转化成纯配电网重构的考虑二阶锥约束的ACOPF 问题。
3.1.1 目标函数
由于考虑了激励机制,且灾害发生后需尽快恢复负荷的供电服务,故目标函数需考虑经济性,且需尽量降低失电量。
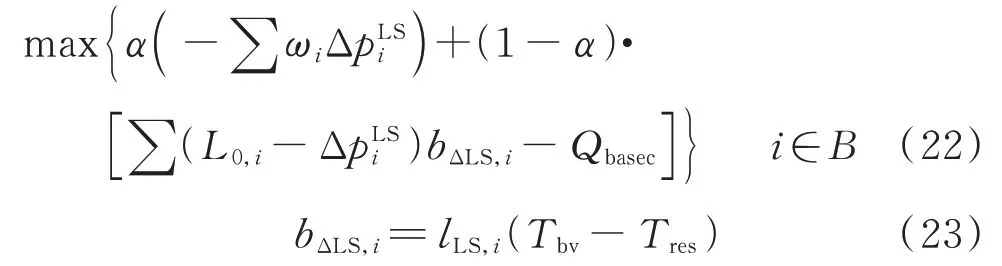
式中:α为比例系数;ωi为节点i的重要负荷权重系数,系统中负荷按重要程度被划分为一级、二级和三级负荷,ωi分别取5、3、1;L0,i为节点i供电恢复前的切负荷量;Δp为节点i供电恢复后的切负荷量;bΔLS,i为节点i恢复单位负荷的综合等效收益;lLS,i为节点i单位时间内单位负荷因失电带来的经济损失;Tbv为供电恢复时长基准值(取人工抢修从故障发生到故障修复所用平均时间);Tres为V2G 参与供电恢复的响应时长;Qbasec为V2G 引导机制补偿给用户的总成本;B为配电网中节点的集合。
3.1.2 约束条件
1)功率平衡约束
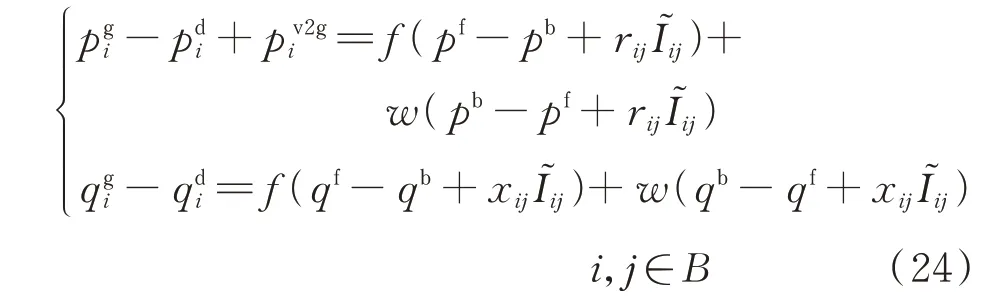
式中:p为与节点i耦合的V2G 交互站点输入功率,当节点i与V2G 站点不相连时为0,否则为1;和分别为流入节点i的有功和无功功率;和分别为流出节点i的有功和无功功率;f和w均是为规定支路ij实际潮流正反方向而引入的0-1 变量,f=1、w=0 为由节点i到节点j的方向;pf和pb分别为从节点i到节点j的功率和从节点j到节点i的功率;I͂ij为流经支路ij电流的平方;rij和xij分别为支路ij的电阻和电抗。
2)节点电压上下限和支路首末端电压约束


3)支路电流上下限约束

4)输入功率上下限约束和支路功率上下限约束

5)切负荷量约束
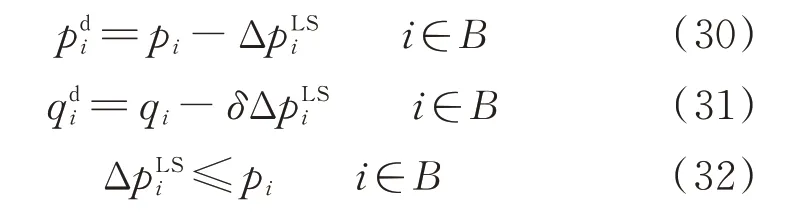
式中:pi和qi分别为节点i的有功和无功功率;δ为功率因数。
6)径向约束/辐射状约束

7)二阶锥约束

当要计算重构后的各参数时,忽略辐射状约束的第1 个约束,优化得到重构后各支路的联络状态dij=+,从而最终获得重构的线路开关方案。
上述模型为一个混合整数二阶锥优化问题,可采用CPLEX 商业求解器直接求解。
3.2 灾后恢复评估指标
为对比V2G 和MEG 在弹性配电网灾后供电恢复中的作用,本文提出了一些评估指标,从系统失电量、响应速度、重要负荷恢复程度等方面体现V2G在配电网弹性提升过程中的优劣性。具体的弹性评估指标内容在附录B 中给出。
本文所提的台风灾害下基于V2G 的城市配电网弹性提升架构详见附录C。
4 算例分析
本文采用改进的IEEE 33 节点配电网和30 节点路网系统为仿真场景。路网与配电网节点对应关系及功能区划分见文献[29]。具体配电网结构如附录D 图D1 所示,图中标出了V2G 站点的编号;负荷按照重要程度被分为一级、二级和三级负荷,所在节点编号如附录D 表D1 所示。
4.1 用户行为特性对V2G 参与供电恢复的影响
在台风灾害影响下,部分EV 用户会选择不出行,即用户的出行意愿可能会发生变化。
附录E 图E1 所示为灾害发生时刻为09:00 且EV 数量为300 时,不同用户出行意愿下各节点V2G参与供电恢复的出力。由图可知,在居民区节点1~17,用户出行意愿越高,V2G 供电恢复出力越低;而在工作区节点18~23,用户出行意愿与V2G供电恢复出力呈正相关。由此可知,灾害发生时的用户出行意愿对各节点V2G 出力影响较大,在后续算例中取用户出行意愿α2=0.8。此外,由于行车速度下降,部分道路还可能出现拥堵情况。
附录E 图E2 所示为灾害发生时刻为20:00 且EV 数量为300 时,道路不同拥堵情况下各节点V2G参与供电恢复的出力。由图可知,拥堵程度增加时,到达居民区节点9~17 处的EV 数量下降,V2G 出力略微降低。由此可知,灾害发生时的道路拥堵情况对各节点V2G 供电恢复出力影响较小。
4.2 V2G 参与供电恢复策略的效果及经济性
为验证V2G 参与供电恢复策略的可行性和适用性,本文设计了以下3 种方案:
1)方案1:仅考虑配电网联络线重构;
2)方案2:在配电网联络线重构的基础上,引入V2G 参与供电恢复;
3)方案3:在配电网联络线重构的基础上,引入MEG 参与供电恢复。
该子算例中,取灾害发生时刻为23:00、EV 数量为300、MEG 数量为6。随机抽取500 组配电网故障场景,对各方案的弹性评估指标进行对比。
1)各方案失电量对比
由表1 可知,联络线重构对失电量的减少有一定帮助,能使灾后配电网失电量降低28.26%;而引入V2G 或MEG 可使失电量显著减少,配合联络线重构,可使灾后配电网失电量分别减少60.18%和53.39%。附录E 图E3 所示为500 组配电网故障场景下各方案的失电量散点图。可见,方案1 的失电量分布较为分散;而方案2 与方案3 的失电量分布大多集中在1 MW 以下,两者分布趋势差别不大。
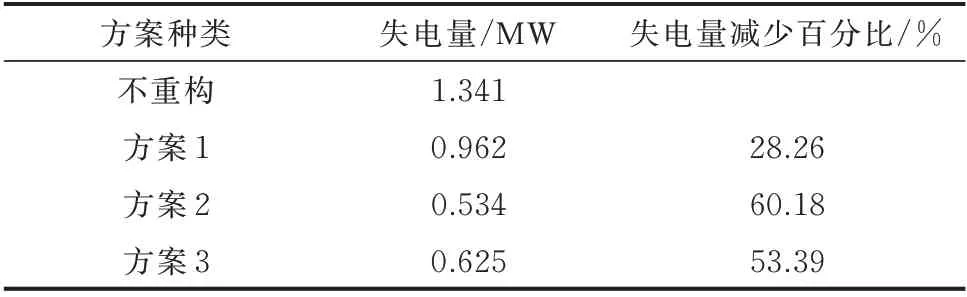
表1 各方案下的失电量对比Table 1 Comparison of power loss in each scheme
由此可见,在考虑配电网联络线重构的基础上,引入V2G 和引入MEG 两种方案在失电量减少方面的效果都较为显著,两者之间区别不大。
2)各方案经济损失对比
由表2 可知,方案3 的等效成本比方案1 增加了43.70%,体现出MEG 参与供电恢复要付出极高的经济代价,符合现今主流弹性提升方案为尽快恢复重要负荷而不惜一切代价的情况;而方案2 的等效成本比方案1 减少了14.68%,体现出V2G 参与供电恢复具有较高的经济性。附录E 图E4 所示为在500 组配电网故障场景下各方案的等效成本散点图。可以看出,方案3 在所有场景下的等效成本都高于50 000 元,而方案1 与方案2 的等效成本大部分都低于50 000 元,其中方案2 的等效成本高于50 000 元的场景个数又明显少于方案1 的场景个数。
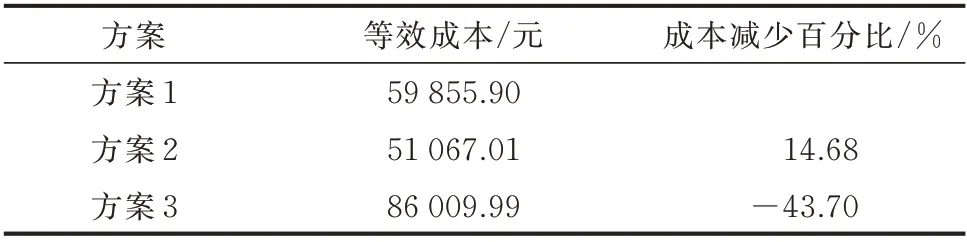
表2 各方案下的等效成本对比Table 2 Comparison of equivalent cost in each scheme
由此可见,在考虑配电网联络线重构的基础上,引入V2G 的方案相比于另外2 种方案在经济损失方面具有明显的优势。
3)各方案响应速度与重要负荷恢复程度对比
由图3 可知,方案1 和2 相比于方案3 参与供电恢复的响应速度明显更快。对于提高一级负荷的恢复程度而言,运用联络线重构操作的作用显著,因此,方案1 已达到了很高的负荷恢复程度,引入V2G和MEG 很难再有大的提升;而对于提高二级负荷恢复程度而言,方案2 相比于方案1 提高了21.98%,方案3 相比于方案1 提高了10.70%。
由此可见,在响应速度方面,方案2 相比于方案3 有明显的优势;在重要负荷恢复程度方面,方案2相比于方案3 作用更显著。
4.3 EV 渗透率与时空特性对方案2 的影响
4.3.1 EV 渗透率的影响
表3 列出了当灾害发生时刻恒定为23:00,且EV 数量分别为200、300、400、500、600 时的各指标对比。随着EV 数量的增加,在其达到500 之前,失电量和等效成本都在不断降低;当EV 数量达到500之后,失电量和等效成本都不再大幅变化。对于重要负荷供电恢复而言,EV 数量对仅使用联络线重构已恢复很好的一级负荷的影响有限,但对提高二级负荷恢复程度效果显著。
由此可见,EV 数量会影响方案2 对配电网弹性提升的结果。在一定范围内,EV 数量越大越可以有效降低系统的失电量,并提高重要负荷供电恢复程度和方案的经济性,但受限于V2G 站点数量、配电网传输能力等因素,在EV 达到一定数量后,其数量的进一步增加无法继续提高恢复效果。
4.3.2 EV 时空特性的影响
本节研究EV 时空特性对方案2 在灾后供电恢复过程中的影响,具体从改变灾害发生时刻和选取典型的EV 空间分布2 个方面进行探讨。
1)灾害发生时刻对方案2 在配电网弹性提升中的影响
图4 所示为当EV 数量恒定为300 时,灾难发生在一天内不同时刻使用方案2 的等效成本和失电量指标变化。
由图4 可得到以下结论:
(1)等效成本和失电量的变化趋势大体近似为“M 型曲线”,且都在07:00 和17:00 达到“高峰”,符合出行链模型中出行行为的正态分布期望值。
(2)夜间和午间时段为“谷期”,且曲线趋势较为平稳。上述2 个时段内EV 大多处于停放状态,愿意响应激励的EV 较多,各V2G 站点出力较高,故失电量处于相对较低的水平。同时,由于愿意响应的车辆较多,激励机制中补偿价格较低,补偿成本和切负荷成本都不高,等效成本处于较低水平。
(3)车辆出行的早、晚高峰(05:00—09:00 和15:00—19:00)为“峰期”,且曲线趋势变化剧烈。上述2 个时段内EV 大多处于行驶状态,愿意响应激励指令的EV 较少,各V2G 站点出力较低。同时,由于愿意响应的车辆较少,激励机制中补偿价格较高,补偿成本和切负荷成本大幅提高,在出行高峰的2 个时刻(07:00 和17:00),等效成本达到最大值。
由此可见,方案2 受灾害发生时刻影响显著,一天内不同时刻能提供的出力和经济性波动较大。
2)EV 空间分布对方案2 在配电网弹性提升中的影响
该子算例选取确定断线场景下的典型EV 空间分布,研究EV 聚集区域不同对供电恢复的影响。附录E 图E5 所示为某确定断线场景下的系统供电分布和范围。由图可知,在该断线场景下,居民区、工作区和休闲区均存在供电效果显著降低的节点。
图5 所示为在该断线场景下,EV 分别聚集在居民区和休闲区内时的系统供电恢复分布和范围。从图5(a)中可以明显看出,当EV 聚集在居民区时,节点13、14、17 和18 处相比于采用方案2 之前的供电效果提升显著,供电比例均达到90%以上;而方案2对另2 个区域的系统节点供电恢复效果有限,节点27、28 和33 处的供电比例均在30%以下。类似的,从图5(b)中可明显看出,当EV 聚集在休闲区时,区内各节点供电恢复效果良好,而另2 个区域内的节点供电恢复效果有限。
综上所述,方案2 受EV 空间分布影响显著,不同区域供电恢复效果差别较大,在EV 聚集的区域系统各节点供电恢复效果较好。
5 结语
本文提出了一种台风灾害下基于V2G 的城市配电网弹性提升策略。首先,考虑台风与线路故障率关系,采用非序贯蒙特卡洛模拟法生成配电网断线场景;其次,考虑灾害下的用户行为改变,建立了EV 群体的灾害前期调度及灾后供电恢复响应模型;然后,在生成灾害场景下,考虑V2G 反向出力求解最优供电恢复策略;最后,提出多个弹性评估指标,验证了所提方法的有效性及可行性。得出主要结论如下:
1)台风灾害会影响道路拥堵情况及用户出行意愿,而EV 的时空分布特性也会因此改变,进而影响V2G 供电恢复出力,其中对道路拥堵情况影响较小、对用户出行意愿影响较大。
2)弹性背景下,引入V2G 参与供电恢复的方案相比于引入MEG 在失电量减少方面作用接近,在经济性和响应速度提升方面优势明显,为现有配电网弹性提升策略提供了新思路。
3)白天V2G 可调动EV 出力相对较少,单位补偿价格高,导致失电量上升,等效成本增大,表明V2G 参与供电恢复的效果受灾害发生时刻和EV 用户的响应行为影响较大,方案的经济性和失电量波动因而较为剧烈。此外,供电恢复效果受EV 空间分布影响较大,当EV 群体集中在某一区域时,该区域供电恢复好,但对周边区域作用有限。
本文研究中,故障场景生成和用户在激励下的响应行为均基于一定的假设,模型偏理想化。后续工作将进一步研究如何提升V2G 在弹性配电网供电恢复中的作用,包括灾后基于能量调度的EV 反向充电引导,以及EV 和MEG 协同参与的配电网供电恢复策略等。
审稿过程中,审稿人与作者的讨论见附录F。
本文在撰写过程中还受到了四川大学电气工程学院向月副教授、何川副教授以及东南大学电气工程学院邢强博士的帮助,特此感谢!
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

