海潮负荷模型对陆态网对流层延迟精度分析

付 饶，潘顺宇，于 冲，宋大鹏，李玉海

（1. 山东正元数字城市建设有限公司，山东 烟台 264670）

由于日、月引力的作用，海平面相对于平均海平面会有周期性的潮汐变化，地壳对海潮的这种海水质量重新分配所产生的弹性效应通常称为海潮负荷[1-3]。大部分研究[4-11]证明，海潮负荷模型会对GNSS 数据结果产生一定的偏差，对沿海区域影响效果更为显著， 因此本文选取中国大陆构造环境监测网络（crustal movement observation network of China，CMONOC）跟踪站观测数据（包括沿海和内陆两部分），在解算过程中分别对有无海潮模型解算方案计算对流层延迟并进行对比分析，其目的是探测海潮负荷模型对CMONOC 网天顶对流层延迟进行精度评估。

1 数学模型

1.1 海潮负荷数学模型

海潮负荷的数学模型一般有球谐函数展开法、负荷格林函数褶积积分2 种方法，本文采用负荷格林函数褶积积分法，海潮负荷可由海潮的瞬时潮高和格林函数褶积积分求取，即[12]：

式中，Lu、Lw、Ls分别为海潮负荷引起的站点径向、西向和南向的位移；ρω为海水密度；φ、λ为计算点的球坐标；φ′、λ′为负荷点的球坐标；t为天文幅角初相开始的时间；ψ为点到负荷点的球面角距；A为计算点到负荷点的球面的方位角；Hi(φ′,λ′,t)为瞬时潮高；U(ψ)和V(ψ)分别为垂直方向和水平方向上的格林函数，具体为：

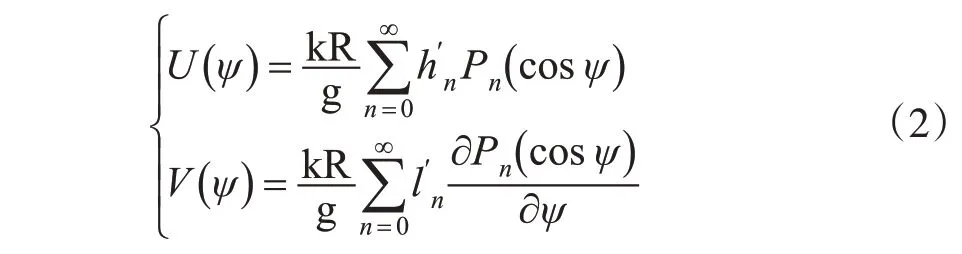
式中，k、g 分别为引力常数和重力常数；R 为地球半径；和为n阶负荷勒夫数；Pn( c osψ)为勒夫让德函数。

一般测站与负荷点的球坐标相互关系表示为：

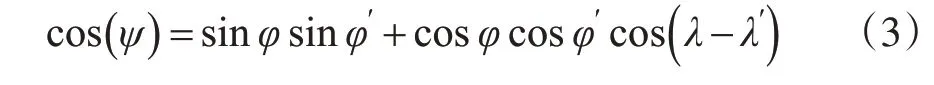
瞬时潮高一般可展开为若干调和分潮潮高的总和，即：

式中，N为叠加潮波数；ωk为各分潮角频率；xk为各分潮天文幅角；ξk和δk分别为各分潮坐标分量的振幅和相位。一般在计算的过程中，海潮负荷只考虑4个半日分潮、4个全日分潮、半月波、月波和半年波等11个主要分潮的影响。

1.2 GNSS计算对流层延迟数学模型

在本次实验过程中利用GAMIT/GLOBK 软件计算对流层天顶总延迟，结合气象观测资料和天顶静力延迟计算模型，得到天顶静力学延迟[13-14]，即：

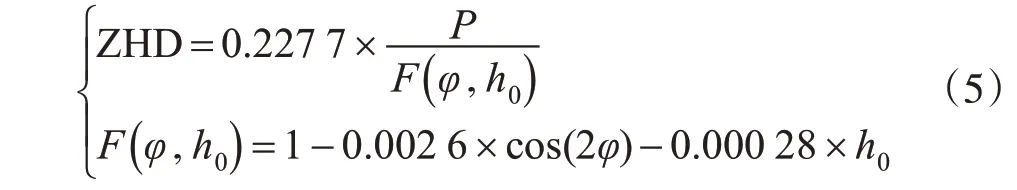
式中，φ为测站的纬度；h0为测站海拔高度；P为测站地面气压；ZHD为天顶静力学延迟。天顶对流层延迟减去天顶静力学延迟（ZHD）得到天顶湿延迟（ZWD），即：

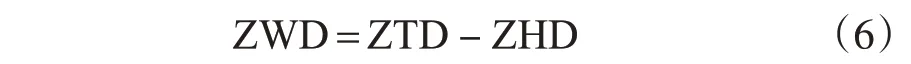
再利用贝叶斯经验公式计算出加权平均温度Tm，进而得到水汽转换系数Π。天顶湿延迟与水汽转换系数相乘即可得到大气可降水量，即：

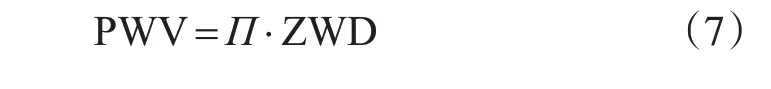
2 数据来源与方案设计

2.1 数据来源

本次实验过程中选取10 个CMONOC 网2019 年年积日071～100，共计30 d 观测数据进行解算，其中站点分布如图1 所示（GDST 站、GDZJ 站、SDRC 站、QHTT 站、XJQM 站、XJQH 站、NMEL 站、MMNS站、NXZW站、HBZG站）。在站点选取原则上尽可能使站点均匀分布，且包含沿海和内陆地区站点，星历产品借助国际GNSS 服务组织（International GNSS service,IGS）中心下载（ftp://cddis.gsfc.nasa.gov）。

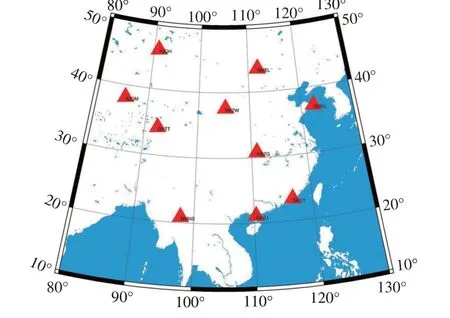
图1 站点分布图

2.2 方案设计

在本次实验过程利用高精度GNSS 数据处理软件GAMIT/GLOBK10.7进行数据处理，分别采用2种方案验证海潮负荷模型对CMONOC网天顶对流层延迟进行精度分析，具体处理策略如表1所示。

表1 解算参数设置

由表1 可知，2 种方案数据处理策略上采用控制变量法，2 种方案唯一不同之处在于解算过程中是否引入海潮负荷模型。在数据处理的过程中，基线处理选择松弛解模式；卫星截止高度角为10°；对流层总延迟计算方式采用萨斯塔莫宁模型；气温气压模型采用目前全球范围内精度最高、使用范围最广的GPT2模型；映射函数采用GMF映射函数模型；大气加权平均温度使用的是贝叶斯模型；解算过程中同时考虑到了相位缠绕、相对论效应对解算结果的影响。

3 案例分析

3.1 海潮模型对沿海/内陆测站适应性分析

本文对2019年年积日071～100的观测数据分别按照方案1 和方案2 进行解算，对比分析沿海区域站与内陆区域站对海潮模型的影响。海潮模型对沿海区域站和内陆区域站ZTD影响残差统计如表2所示。

由表2 可知，海潮负荷模型对沿海和内陆测站解算ZTD影响存在差异性，海潮负荷模型对沿海地区测站ZTD影响误差明显高于内陆地区测站ZTD误差。在沿海地区测站中，在GDST 站ZTD 最大误差达到了15.42 mm；而在内陆地区测站中，在MMNS站ZTD最大误差达到了6.04 mm；通过对表2 中内陆测站ZTD影响残差进行分析，可以看出测站距离海域的距离越远，对ZTD影响越小，ZTD的精度越高，反之亦然。

表2 海潮负荷模型对沿海/内陆测站ZTD影响残差统计

3.2 海潮负荷模型对PWV影响

为了进一步对比分析海潮负荷模型对CMONOC网天顶对流层延迟，图2 分别给出了海潮负荷模型对不同测站PWV影响的时间序列。

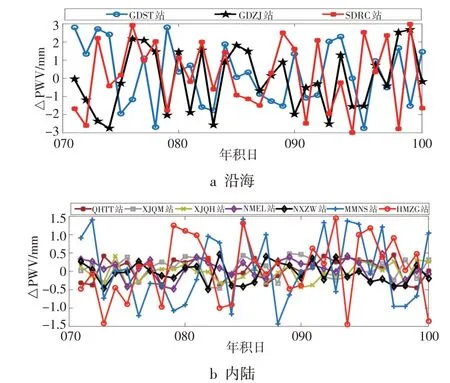
图2 海潮负荷模型对沿海/内陆测站PWV影响时间序列

由图2可知，海潮负荷模型对沿海地区测站PWV影响误差在区间[-3 3]内，就内陆地区而言，MMNS站和HMZG 站PWV 影响误差在区间[-1.5 1.5]内，而QHTT站、XJQM站、XJQH站、NMEL站、NXZW站PWV影响误差在[-0.5 0.5]内，进一步证实了测站距离海域的距离越远，对PWV影响越小，PWV的精度越高。因此，在高精度GNSS水气反演过程中必须考虑到海潮负荷对PWV的影响，应引入海潮负荷模型提高反演的精度。

4 结 语

本文基于CMONOC观测数据验证了海潮负荷模型对沿海地区和内陆地区测站ZTD 和PWV 影响，实验结果证实了测站距离海域的距离越远，对ZTD、PWV影响越小，ZTD、PWV的精度越高，对沿海地区测站反演ZTD 会产生厘米级误差，对PWV 信息产生毫米级误差，对内陆地区测站反演ZTD和PWV信息均产生毫米级误差。因此，在高精度GNSS 数据处理与测量过程中，应考虑到海潮负荷对测站信息的影响，选取合适的模型对海潮负荷进行改正。