计及交通流量动态变化的配电网灾后修复多时间断面优化策略

万海洋，刘文霞，石庆鑫，何 剑，孙为民，张晓涵

（1. 华北电力大学电气与电子工程学院，北京市 102206；2. 中国电力科学研究院有限公司，北京市 100192）

0 引言

近年来，随着全球气候变暖，极端天气导致自然灾害频发，多次引发电力系统大规模的停电事故；加之城市基础设施间的交互影响，造成了愈发严重的社会动荡和经济损失［1］。为提升电力系统在面对此类低概率、高影响灾害时的抵御能力和恢复能力，国内外学者和电力企业针对灾后故障设备的抢修和失电负荷的恢复开展了大量的研究和实践工作［2］。然而在“双碳”战略目标的推动下，电力在能源末端的占比不断提高，且配电网形态、源荷特性都发生了深刻变化［3］。如何计及外部影响、充分利用灵活性资源开展灾后优化修复的研究，对降低停电损失、减少社会影响具有重要实际意义。

在极端灾害发生后，电力系统可采取的应急修复手段包括优化调度抢修小队抢修故障设备和利用电网应急资源恢复负荷2 个方面工作［4］，但由于故障抢修和负荷恢复二者间具有时序耦合的特性［5］，现有研究通常会采用多时间断面优化方法协调2 个过程［6-12］。同时，由于新型电力系统的发展，配电网中蕴含的灵活性资源的种类不断增多。国内外研究中采用的应急恢复资源逐步由研究初期的分布式电源［6］、远程/手动开关［7］扩展至微能源网［8］、风光储系统［13］等。文献［8］建立了计及故障元件抢修与负荷时序性的配电网故障恢复模型，并采用多时间断面方法交替迭代求解。此外，近年来随着电动汽车等移动式资源的兴起，移动式储能车［13-14］、移动式电源车［15-16］等也能够作为灵活供电资源在灾后修复过程中起到支撑负荷正常工作的作用。根据生成移动式资源行驶时间方法的不同，现有规划移动式资源路径的方法可分为2 类：其一为根据地理位置生成或随机生成行驶时间［6-10］；其二为建立交通网络的模型，用路口延误时间、道路拥塞程度评估道路通行畅通与否［11，13］。另外，也有研究将移动式资源的调度问题建立为两阶段鲁棒优化模型，在车辆行驶时间最恶劣的条件下，多时间断面制定了负荷恢复计划［12］。但以上研究均忽略了道路交通流量在灾害过程中会随时间不断变化的过程，均未涉及移动式资源的行驶时间、行驶路径与交通网络堵塞情况的相关性分析。由于未来将会有更多的移动式资源参与到配电网灾后复电的过程中［17］，而灾害场景下交通网络对移动式资源的作用对故障抢修顺序和恢复资源调度计划的决策结果有很重要的影响。因此，计及交通流量时变性的研究仍有待深入。

此外在故障修复的整个过程中，配电网需要始终满足辐射状和连通性约束［18］。文献［19］提出的单一商品流（single commodies flow，SCF）理论在混合整数规划模型中确保了图的辐射状与连通性关系。针对该方法中孤岛数目必须与电源数相等的弊端，文献［20］提出了改进单一商品流（modified single commodies flow，MSCF）理论，实现了多孤岛融合和孤岛数目在线优化，但当系统中出现不能与任一源节点连接的失电节点时，该约束将不再满足。然而在极端灾害下，故障位置具有较大的随机性，如何提高配电网网架重构模型对随机故障场景的适应性仍需进一步研究。

为此，本文针对灾害场景建立了计及交通流量动态变化特性的预测模型，并基于MSCF 理论提出了一种灾后故障修复多时间断面优化策略。该策略通过多次更新交通流量信息，保证了故障设备修复时间的预测与故障抢修和负荷恢复策略的制定更加符合实际情况，更利于提高配电网韧性。

1 故障设备修复时间预测模型

1.1 预测故障修复时间的必要性

故障设备的修复时间可以划分为抢修时间和行驶时间2 个部分［9］。对于前者，本文假设在灾害发生后，抢修小队已提前采用无人机侦测等手段预测了各个故障的抢修时间。但由于后者行驶时间的长短取决于抢修车选择的行驶路径的拥塞情况，如何结合实际交通网络交通流量的分布，为抢修车选择一条用时最短的路径对缩短用户停电时间尤为重要。基于此，本节首先采用元胞传输模型（cell transmission model，CTM）建立交通网络模型，并采用Wardrop 第二平衡原理。其次，采用美国联邦公路局（Bureau of Public Road，BPR）路阻模型和Dijkstra 最小路径算法搜索用时最短的路径。

1.2 交通网络的CTM

由于各条道路在不同时段的交通流量具有随机性，导致车辆在各时段通过同一道路的时间是不同的。采用CTM 建立交通网络模型可以很好地解决交通流量动态变化的问题［21］，该理论提出，当交通网络的流量与密度之间满足一定关系时，时间可以被划分为多个微小的间隔，此时可以将连续的交通网络划分为多个具有长度和方向的元胞，元胞的长度代表车辆在单位时间内自由行驶的距离，元胞的方向代表道路方向。本文基于配电网沿道路铺设的原则，建立了交通网络的元胞结构，见附录A 图A1。

1.3 道路交通流量预测模型

Wardrop 第二平衡原理提出在交通网络平衡的基础上，交通流量应按照总出行成本最小来分配。基于此，本节在将交通网络的道路结构转换为元胞结构后，定义目标函数为最小化全部元胞内的交通流量之和［22］，如式（1）所示，并在式（2）—式（7）的约束下，根据交通网络当前时刻元胞内流入及流出的流量，预测之后各时刻各元胞内的交通流量。由于各式中元胞i均满足∀i∈STN，时间变量t均满足∀t∈ST1，其中，STN为交通网络全体元胞的集合，ST1为一天中各时刻的集合，为书写简便，故省略。

式中：ϖi，t为元胞i在t时刻交通流量的预测值；χki，t为t时刻从元胞k流向元胞i流量的预测值；Sin(i)和Sout(i)分别为元胞i的上游和下游元胞集合；Χmaxi为能够流入或流出元胞i的最大流量；ϖmaxi为元胞i内能够容纳的最大流量；οi，t0为在初始时刻t0元胞i内的流量；ζij，t0为在初始时刻t0从元胞i流向元胞j的流量。式（2）表示交通流量守恒；式（3）表示t时刻从元胞i流出的流量不大于元胞i当前存在的流量；式（6）表示t时刻流入元胞i的流量不大于此时元胞i内还能够容纳的流量。

1.4 故障修复时间计算

根据BPR 路阻函数［23］，可以将各类道路在各时刻的交通流量转换为车辆在各类道路上的实际行驶时间，如式（8）所示。

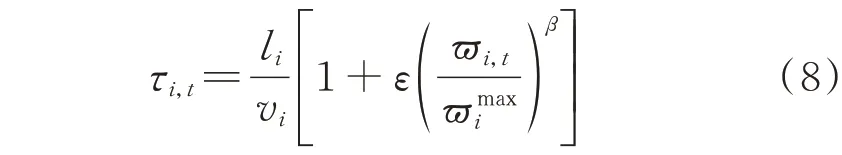
式中：τi，t为抢修小队在t时刻通过元胞i的实际行驶时间；li为元胞i的长度；vi为抢修小队通过元胞i的自由速度；ε和β为元胞i的特征参数，取值由元胞对应道路的种类而定。

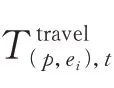
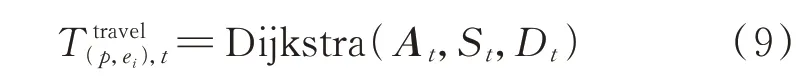
式中：Dijkstra(·)表示采用Dijkstra 算法求解。

叠加故障设备ei的抢修时间Trepairei，t，即可得到故障设备ei的修复时间T(p，ei)，t，如式（10）所示。

2 计及交通流量动态变化的故障修复策略

当预测出各故障的修复时间后，即可开始制定故障修复策略。本章以负荷削减量与恢复资源调度成本最小为目标，在固定式/移动式恢复资源运行约束、配电网运行约束与网架动态重构约束的条件下，建立混合整数线性规划模型，并采用多时间断面优化方法，即在每个故障修复完毕时重新预测交通流量，并更新剩余故障的抢修顺序和恢复资源的调度计划。

2.1 目标函数

式中：ST2为整个故障修复过程的时间集合；Δt为时间步长；SCL和SNL分别为关键工商业和普通居民用户负荷节点集合；cCL和cNL分别为关键工商业和普通居民用户负荷单位削减成本；ΔP为节点j上负荷在t时刻的有功功率削减量；SES为储能节点集合；cES为储能充入单位电量的费用；Pi，t为节点i上储能在t时刻吸收的电功率；SDG为分布式电源节点集合；cDG为分布式电源（燃气轮机等）单位发电量的出力成本；PDGi，t为节点i上分布式电源发出的电功率；SMES为储能车集合；SN为配电网节点集合；PSm，i，t为节点i上连接的第m号储能车在t时刻的充电功率；cMES为储能车单位时间的行驶费用；θm，t为表示第m号储能车在t时刻行驶状态的0-1 变量，若储能车处于行驶状态，则θm，t=1，否则θm，t=0。

目标函数式（11）主要由2 个部分构成，前2 项代表电网2 类负荷的削减损失，后3 项为应急恢复资源调度费用（固定式储能充电费用、分布式电源出力费用、移动式储能车的充电成本和行驶费用）。计及后3 项的原因是为了避免当负荷恢复完毕时分布式电源和储能不必要的工作过程［14］，且由于后3 项数值的数量级一般均小于前2 项，所以目标函数式（11）的主体仍然是追求最小化电网负荷削减量。

2.2 约束条件

2.2.1 固定式恢复资源运行约束

本文考虑的固定式恢复资源包括储能、分布式电源、光伏和可削减负荷，其中式（12）—式（16）为固定式储能设备充放电约束；式（17）为分布式电源放电约束；式（18）为分布式光伏出力约束；式（19）为可削减负荷削减量约束。由于各式中时间变量均满足∀t∈ST2，为书写简便，故省略。

2.2.2 移动式恢复资源运行约束

1）抢修小队

抢修小队调度需要满足约束式（20）—式（24），由于各式中故障设备均满足∀ei∈SF，时间变量均满足∀t∈ST2，其中，SF为故障设备集合，为书写简便，故省略。式（20）代表故障设备修复总时长为常数；式（21）和式（22）代表抢修小队在故障修复状态未改变前，应在连续的时间内前往故障点并完成抢修工作；式（23）代表故障设备修复完毕后不会再次发生故障；式（24）代表在同一时刻下，正在被抢修的故障设备数目不大于抢修小队数目；式（25）代表当故障设备ei为故障状态时，其对应的开关必须断开，但当ei已修复时，其对应开关既可闭合也可断开。

2）移动式储能车

移动式储能车调度需要满足约束式（26）—式（33），由于各式中储能车变量均满足∀m∈SMES，时间变量均满足∀t∈ST2，为书写简便，故省略。式（26）代表储能车的行驶状态和连接状态互斥；式（27）代表当储能车在t时刻与节点i相连时，至少需要经行驶时间Ttravel(i，j)，t后才能与节点j相连；式（28）代表一辆储能车在一个时刻仅能与一个充换电站连接；式（29）代表储能车当且仅当接入充换电站时，方可进行充放电；式（30）—式（33）代表储能车充放电功率与容量间的关系。

配电网运行约束需要满足式（34）—式（42），由于各式中时间变量均满足∀t∈ST2，配电网节点均满足∀j∈SN，配电网支路均满足∀i-j∈SB，其中，SB为配电网支路集合，为书写简便，故省略。式（34）和式（35）为有功和无功功率平衡约束；式（36）—式（38）为支路开关状态约束；式（39）为线性Distflow 描述支路潮流约束［24-25］，当wi-j，t=0 时，即支路i-j的开关断开时，该支路潮流与节点电压间的关系被松弛；式（40）和式（41）为线性化后的支路容量约束［26］；式（42）为节点电压约束。

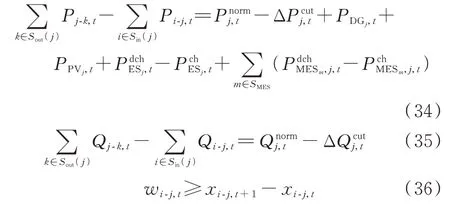
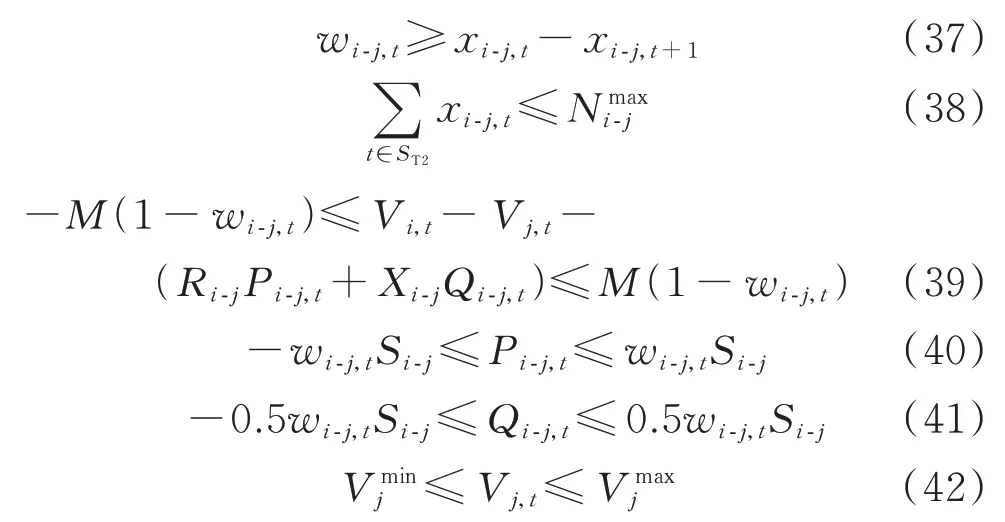
式中：Pj-k，t为支路j-k在t时刻的有功潮流；Sout(j)和Sin(j)分别为节点j下游和上游节点集合；Qj-k，t为支路j-k在t时刻的无功潮流；Q为负荷节点j上在t时刻的无功功率正常值；ΔQ为负荷节点j上在t时刻的无功功率削减量；wi-j，t为表示支路i-j在t时刻开关状态的0-1 变量，当开关闭合时wi-j，t=1，否则wi-j，t=0；xi-j，t为表示支路i-j的开关在t时刻动作状态的0-1 变量，若开关动作，则xi-j，t=1，否则xi-j，t=0；N为支路i-j开关动作次数的最大值；Ri-j和Xi-j分别为支路i-j的电阻和电抗值；Si-j为支路i-j的容量；Vj，t为t时刻节点j电压，Vmaxj和Vminj分别为其最大、最小值。

2.2.4 网架动态重构约束

为了提高网架动态重构算法对于故障场景的适应性，保证失电节点与未失电节点均能满足辐射状约束，本文基于SCF 理论提出了MSCF 理论。如图1 所示，以9 节点8 支路的有源配电网为例，该方法通过增加虚拟根节点R与各失电节点（图中5、6、9节点）间生成一对一连接的支路，构成一个虚拟孤岛。在每次网架开关变化的过程中，检测各负荷节点的失电状态，并动态添加和删减虚拟孤岛中的节点数目，从而保证整个配电网始终能够满足辐射状约束，提高算法对故障场景的适应性。此时配电网网架动态重构可以由辐射状约束式（43）和连通性约束式（44）—式（48）来描述。

图1 基于MSCF 理论的虚拟拓扑Fig.1 Virtual topology based on MSCF theory

1）辐射状约束

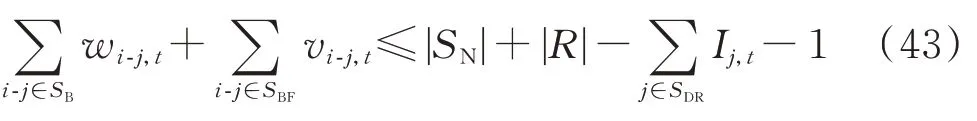
式中：vi-j，t为表示虚拟失电网络部分中支路i-j开关状态的0-1 变量，当开关闭合时vi-j，t=1，否则vi-j，t=0；SBF为新增失电虚拟网络支路集合；|SN|为节点集合中的节点数量；R为由失电负荷组成的虚拟孤岛的根节点，|R|为虚拟根节点的数量；SDR为由恢复资源构成的源节点集合；Ij，t为判断源节点j能否作为某一孤岛的根节点的0-1 变量，当源节点j能作为根节点时Ij，t=1，否则Ij，t=0。

以图1 为例，配电网中有故障设备e2、e6、e8，共3 处支路故障，当采用本节提出的方法时，此时配电网被划分为3 个部分，分别为：与源节点1、8 相连的区域（孤岛1）、与源节点4 相连的区域（孤岛2）、不与任何源节点相连的区域（虚拟孤岛3），约束式（43）不等号左侧闭合的开关为w1-2，t+w2-7，t+w7-8，t+w3-4，t+vR-5，t+vR-6，t+vR-9，t=7，右侧为|SN|+|R|-I1，t-I4，t-1=7，满足约束式（43），配电网辐射状拓扑成立。但当采用文献［17］中的辐射状约束时，需要满足w1-2，t+w2-7，t+w7-8，t+w3-4，t=|SN|-I1，t-I4，t，显然此时辐射状约束是不成立的。

2）连通性约束

当节点j为未失电状态，即aj，t=1 时，此时节点j可能为根节点、源节点或负荷节点，前两者节点功率平衡如式（44）所示，后者节点功率平衡如式（45）所示，支路潮流与支路开关间的限制如式（46）所示。

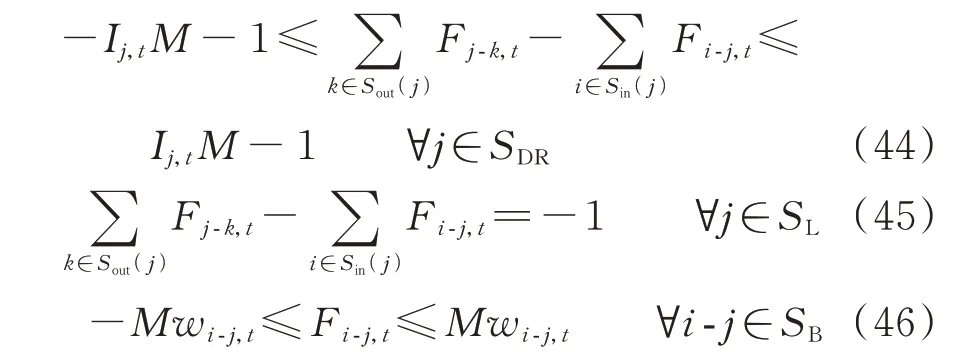
式中：Fj-k，t为虚拟网络中支路j-k在t时刻的潮流；SL为负荷节点集合。约束式（44）代表当源节点j作为根节点，即Ij，t=1 时，不对该节点的流入流出功率做限制，否则当Ij，t=0 时，源节点j应被当作PQ节点，与负荷节点满足相同的约束式（45）。约束式（46）限制了Fi-j，t≠0 当且仅当支路i-j的开关闭合时成立。

当节点j为失电状态，即aj，t=0 时，失电节点与根节点R之间的潮流约束如式（47）所示，支路潮流与支路开关间的限制如式（48）所示。

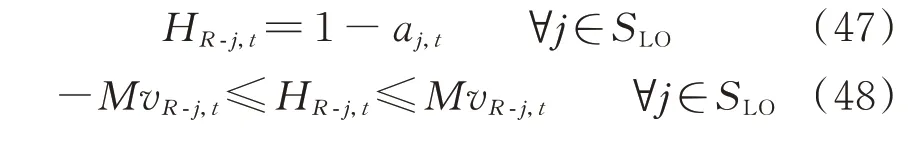
式中：HR-j，t为虚拟失电网络中根节点R与失电节点j间的支路潮流；SLO为失电负荷节点集合。

2.3 求解流程

本文具体求解流程如图2 所示。假设在t0时刻极端灾害导致电力系统发生多处故障。

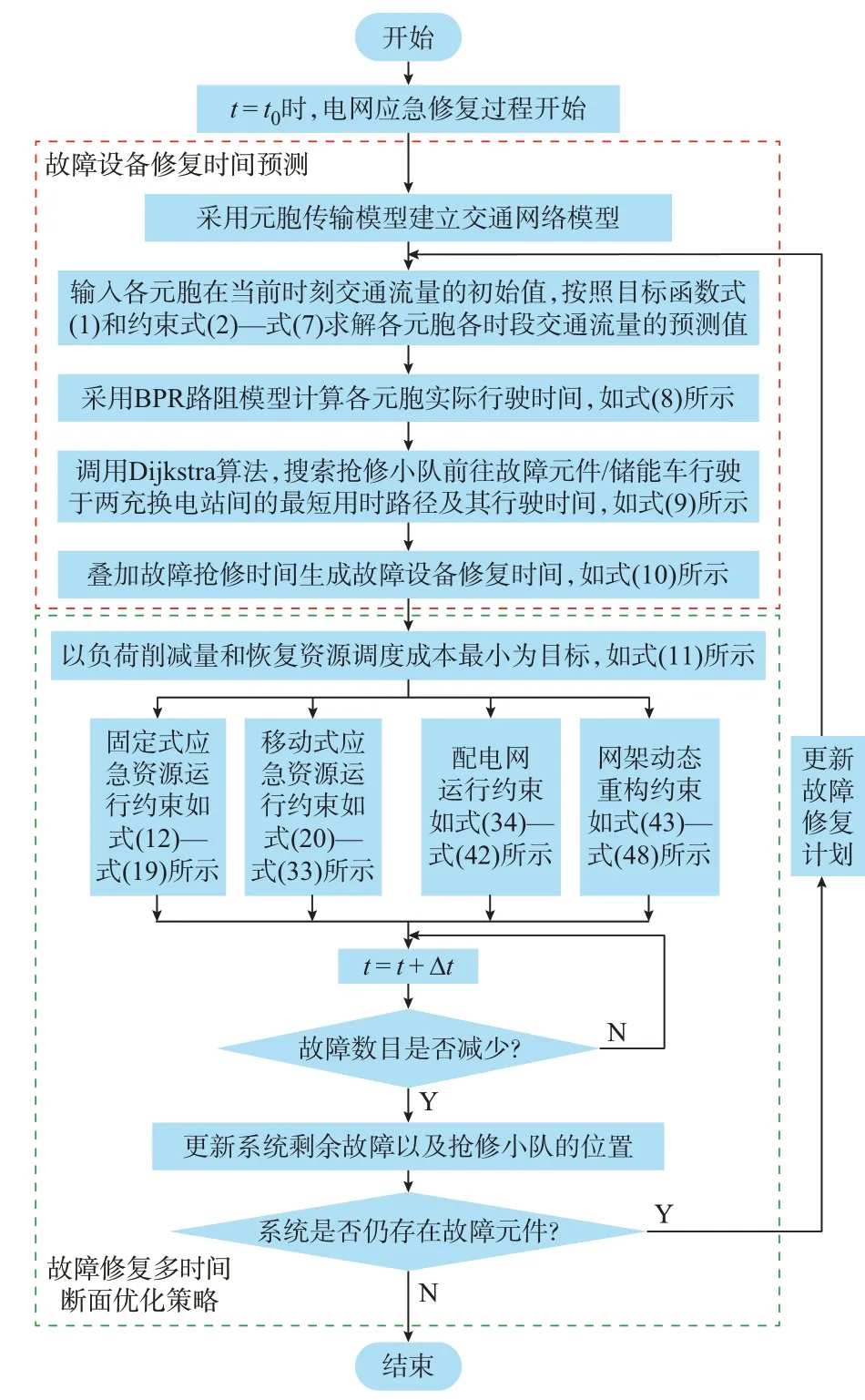
图2 故障修复的多时间断面优化策略求解流程图Fig.2 Flow chart of multi-time-section optimization strategy solution for fault recovery

在故障设备修复时间的预测过程中，首先，采用CTM 建立交通网络并根据式（1）—式（7）预测交通流量。其次，采用BPR 路阻模型和Dijkstra 算法搜索两点间用时最短的路径与行驶时间。最后，叠加故障抢修时间得到故障设备的修复时间。

在制定故障抢修和负荷恢复策略的过程中，首先，根据式（11）—式（48）优化决策该时间窗内故障设备的抢修顺序和恢复资源的调度计划。其次，在下一时刻判断故障数量是否减少，若是，则更新系统剩余故障以及抢修小队位置；此时若系统中仍存在故障设备，则重复上述流程，更新故障修复计划，直至全部故障均抢修完毕。

3 仿真算例

本文构建的混合整数线性规划问题可以利用现有的成熟商业求解器例如CPLEX 和GUROBI 等进行求解，本文具体是在MATLAB R2021a 中建模并通过YALMIP-CPLEX 进行求解。

3.1 仿真参数

配电网采用改进IEEE 33 节点配电系统，见附录A 图A2。配电网中共含2 套光储设备、2 台分布式电源、1 辆移动式储能车、1 个抢修小队，各设备参数见附录A 表A1 和表A2；关键工商业、普通居民负荷的单位削减成本分别为1.5 元/(kW·h) 与0.5 元/(kW·h)；抢修小队和移动式储能车初始位置位于节点1；开关动作最大次数为3。交通网络见附录A 图A1，该交通网络共含33 个节点，74 条道路，根据文献［27］可将道路划分为快速路、主干路、次干路和支路，各类道路与之对应元胞的参数见附录A 表A3。

3.2 故障场景及解决策略

为分析并验证本文提出的配电网故障修复策略的有效性，本文以故障线路最初是否会产生失电节点为基准，设计了2 种故障场景，如表1 所示。

表1 故障场景参数Table 1 Parameters of fault scenarios

本文根据求解方法和网架重构约束的不同，制定了3 类故障修复策略进行仿真测试，具体如下：

策略1：求解方法采用本文提出的多时间断面优化策略，但网架重构约束采用传统SCF 理论，其余负荷恢复和故障抢修模型与本文相同；

策略2：网架重构约束采用本文提出的MSCF理论，但求解方法采用单时间断面优化策略，其余负荷恢复和故障抢修模型与本文相同；

策略3：采用本文所提方法，网架重构约束采用MSCF 理论，求解方法采用多时间断面优化策略。

3.3 结果分析

3.3.1 故障场景1

在故障场景1 下，由于最初的故障线路导致网络中出现失电节点，策略1 的网架重构方法不再适用，此处主要对比分析策略2 与3 的求解结果。

1）决策结果

当采用策略2 时，制定的故障设备抢修顺序为e4→e1→e2→e3→e5，预计分别在时刻53、63、72、82、93 修复完毕；移动式储能车分别于时刻46 至63、时刻65 至93 在充换电站点7 和17 充放电，系统总经济损失为17 336.2 元，求解总时间为86.4 s。移动式资源工作情况如图3（a）所示，网架动态重构情况和负荷缺损量、应急资源工作情况分别如附录B图B1 和图B2（a）所示。

图3 移动式资源工作情况(策略3：场景1)Fig.3 Operation situation of mobile resource (strategy 3:scenario 1)

当采用策略3 时，在各个故障修复完毕时刻重新预测道路交通流量，并更新故障的预测修复时间，经多次决策后得到故障设备的最优抢修顺序为e4→e1→e2→e5→e3，预计分别在时刻53、62、71、81、92 修复完毕；移动式储能车分别于时刻46 至62、时刻65 至92 在充换电站点7 和17 充放电，系统总经济损失为16 305.9 元，求解总时间为387.2 s。由于文章篇幅限制，仅展示前3 次决策时刻的移动式资源工作情况，如图3 所示，网架动态重构和负荷缺损量、应急资源工作情况分别如图4、图5 所示。

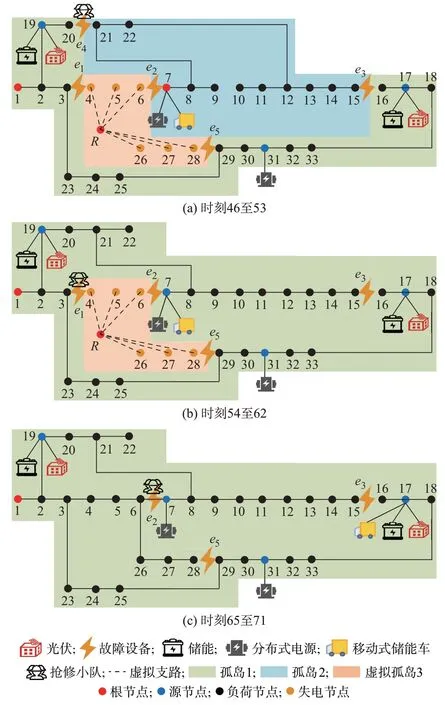
图4 网架动态重构情况(策略3：场景1)Fig.4 Dynamic reconfiguration situation of grid(strategy 3:scenario 1)

图5 负荷缺损量和应急资源工作情况(策略3：场景1)Fig.5 Amount of load loss and operation situation of emergency resources (strategy 3: scenario 1)

2）移动式资源工作情况的对比分析

对比图3（a）至（c）可以发现，由于策略2 未考虑交通网络交通流量随故障修复过程的不断变化，将车辆行驶时间定为常数化处理，则抢修小队和移动式储能车始终执行初始时刻的决策计划，不再更新修改抢修顺序和充放电计划；而策略3 则会考虑到交通流量动态变化的影响，如图3（b）所示。当故障设备e4于时刻53 修复完毕时，由于当前元胞34、43、42、41、40 和39 内的交通流量增加，按照原行驶前往故障设备e1的行驶时间会大大增加，重新决策后抢修小队选择了更优的行驶路线：元胞56 →55 →54 →2 →3。此后，当故障设备e1和e2分别于时刻62 和71 抢修完毕时，此时策略3 会再次更新交通流量信息，并重新预测剩余故障设备e3和e5的修复时间，经最优决策后更新抢修顺序为e5→e3，并预计分别在时刻81 和92 修复完毕。此外，储能车也因为故障设备e1的提前修复，在时刻62 即出发前往充换电站点17，但由于此时沿途交通流量较大，行驶共耗时3Δt，与策略2 中储能车到达充换电站的时刻相同。总而言之，策略3 通过多次更新交通流量信息，为移动式恢复资源规划用时更短的抢修顺序和路径，缩短了故障修复的总时长，较策略2的系统经济损失减少了1 030.3 元。

3）网架动态重构分析

在时刻46 至53，见图4（a），网络中共含3 个孤岛，其中孤岛1 中含有多个源节点，但节点1 与上级电网相连接，调节余量更加充足，被选作为根节点；孤岛2 中仅含有由分布式电源和移动式储能车构成的源节点7，则根节点为7；此外，虚拟根节点R通过闭合与4、5、6、26、27 和28 共6 个失电节点间的虚拟支路开关，构成虚拟孤岛3；校验辐射状拓扑约束式（43） ， ∑wi-j，t=25， ∑vR-j，t=6， |SN|=33，∑Ij，t=2，约束成立。在时刻54 至62，见图4（b），由于故障设备e4在时刻53 修复完毕，线路20-21 开关闭合，孤岛1 与孤岛2 融合，此时网络中共存在2 个孤岛，根节点分别为节点1 和节点R，∑wi-j，t=26，∑vR-j，t=6，|SN|=33，∑Ij，t=1，辐射状拓扑约束仍旧满足。在时刻65 至71，见图4（c），由于故障设备e1在时刻62 修复完毕，当线路3-4 开关闭合后，此时系统中将不再存在失电节点，所有负荷节点均能与根节点1 连接。但此时由于系统中仍存在部分故障线路，受线路容量的限制，下游负荷并不能完全恢复供电，所以移动式储能车移动至充换电站17 进行放电。

3.3.2 故障场景2

1）决策结果

在故障场景2 下，3 种策略求解得到的目标函数和移动式资源工作情况如表2 所示，固定式资源工作情况分别如附录B 图B2（b）至（d）所示。

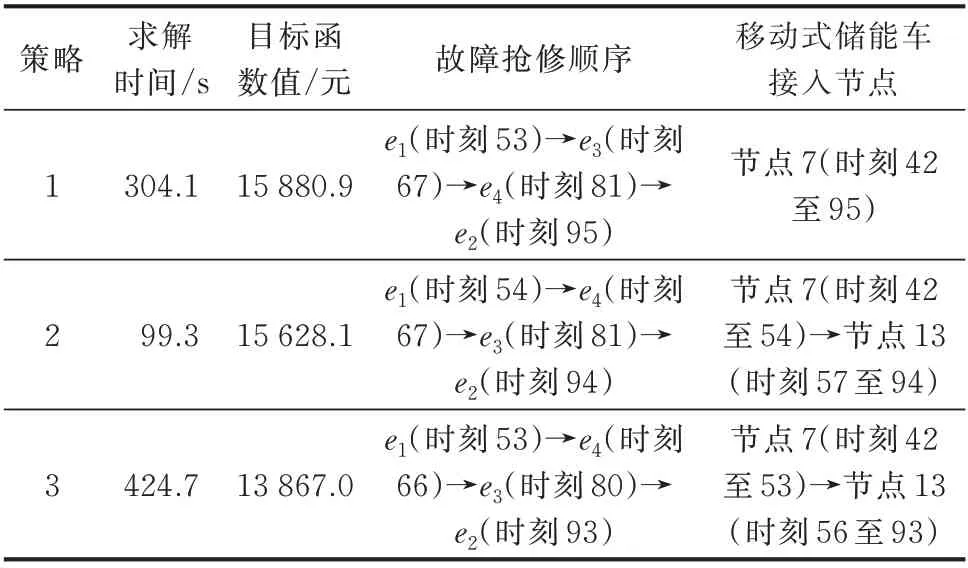
表2 故障场景2 下移动式资源的求解结果Table 2 Solution results of mobile resources in fault scenario 2

2）策略2 与策略3 对比分析

在故障场景2 下，策略2 与策略3 求解结果的规律与在故障场景1 中类似，但由于策略2 为单时间断面决策，决策变量数目远远小于策略3，所以策略2 的求解时间较短，具体对比分析详见附录C。

3）策略1 与策略3 对比分析

对比附录B 图B2（b）和（d）可以发现，虽然策略3 较策略1 求解时间增加了120.6 s，但系统总经济损失减少了2 013.9 元，并且更能降低普通居民负荷的削减量（图中绿线与红线间的部分）。这是由于策略1 在整个修复过程中仅需要保持网络中孤岛数目恒定，约束条件数目略少于策略3，求解难度略微有些降低，但这也导致部分容量足够大的源节点不能充当根节点支撑附近负荷的正常运行；而策略3 在调度开关动作的同时，考虑了各类应急资源形成孤岛、支撑负荷工作的作用，储能车能够在上游故障修复完毕时，前往充换电站17 充当根节点，保证下游负荷的正常运行，实现了多孤岛根节点的动态选择和范围的动态融合。

3.4 交通流量的影响分析

为确定策略3 对交通流量大小的灵敏性情况，本文设计交通流量初始值分别为故障场景1 的110%、140%和170%，测试结果如表3 所示。

观察表3 可知，当移动式资源的行驶时间随交通流量增加而增加时，一方面，抢修小队需要花费更多时间前往故障点，各个故障修复完成的时间有不同程度增加；另一方面，储能车由于来不及前往失电负荷处紧急供电，造成资源利用效率大大降低，最终导致系统负荷总缺损量和资源调度成本大幅增加。

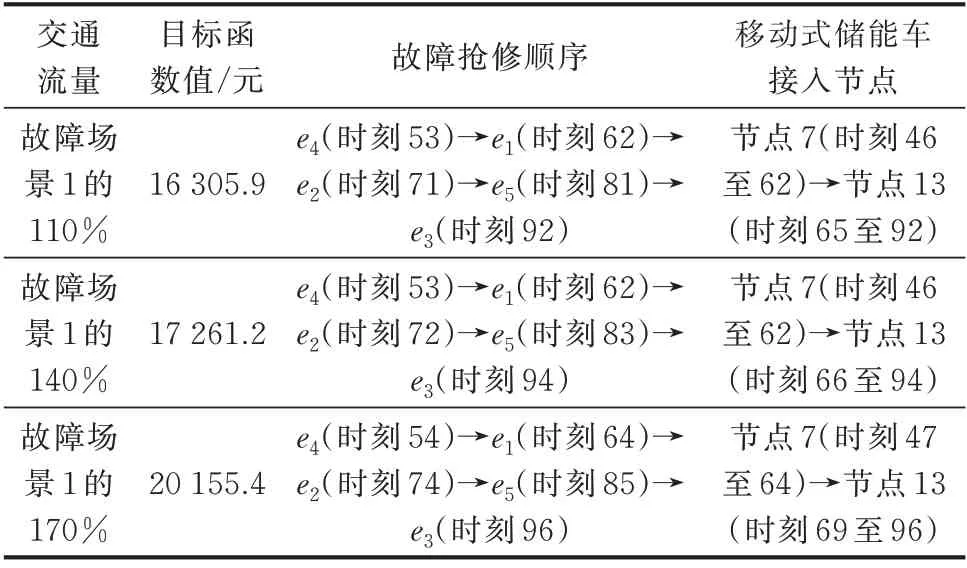
表3 交通流量大小灵敏性分析结果Table 3 Sensitivity analysis results of traffic flow

3.5 光伏、负荷误差和时间步长的影响分析

考虑到在实际故障修复的过程中，光伏、负荷大小会受天气影响而产生不同程度的波动，可能会导致配电网失电负荷恢复结果不佳，本节设计了误差值ϕ和求解时间步长Δt分别为5%、10%、15%以及15、30、60 min，以确定本文所提出的方法对光伏、负荷不确定性因素和求解时间步长的灵敏性情况，测试结果如表4 所示。

表4 光伏、负荷误差和时间步长灵敏性分析结果Table 4 Sensitivity analysis results of photovoltaic,load error and time step

表4 中：ι1为根据原始数据仿真计算出的系统经济损失；ι2为根据预测出的数据有误差时仿真计算出的系统经济损失；残差κ=(ι2-ι1)/ι1。观察表4中的9 组仿真结果可以得到以下结论：

1）在同一误差水平下，求解时间步长越短，残差有不同程度降低，但求解时间也随之大幅升高。这是因为随时间步长的缩短，系统可以更充分、精细地调度各类应急资源，使得ι1能够与ι2较好地吻合；但同时由于决策次数的增加，计算负担也会大大增加。

2）在同一求解时间步长下，光伏、负荷的预测误差越大，残差也随之增大。这是因为随预测误差的增大，仿真计算时采用的实际数据偏差越大，最终系统采用了不符合实际情况的故障修复策略，导致配电网实际经济损失ι2大大增加。

4 结语

本文提出了一种计及交通流量动态变化的故障修复多时间断面优化策略，制定了更加符合实际情况的故障设备抢修顺序和恢复资源调度计划，提高了网架动态重构约束对随机灾害场景的适应性，为进一步从故障修复过程中提升配电网韧性给出了一种较为新颖的解决思路。具体结论如下：

1）交通流量动态变化对移动式资源的行驶路线的影响是很大的，采用多时间断面的优化策略可以为移动式恢复资源规划用时更短的路径，缩短故障修复的总时长，降低系统总停电损失；

2）当交通流量处于较高水平时，由于移动式资源的行驶时间增加，会导致系统经济损失大幅增加。此时，灾前优化选择移动式资源驻点并合理配置固定式资源容量将提高系统韧性。

在未来的工作中，研究在极端灾害场景下，如何计及交通网络的影响，对移动式和固定式资源进行灾前优化配置具有实际意义。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。