山区河流大水位差直立式框架码头静力弹塑性计算
邓方明,文训科,谢 峰
(1.四川岷江港航电开发有限责任公司,乐山 614001;2.四川省交通勘察设计研究院有限公司,成都 610017)
在《建筑抗震设计规范》附录M“实现抗震性能设计目标的参考方法”中,推荐采用静力弹塑性分析(即Pushover分析)对结构开裂后的抗震参数进行估算[1],《水运工程抗震设计规范》对码头结构抗震计算主要采用底部剪力法和反应谱振型分解法,还未采用静力弹塑性分析方法[2]。李颖等[3]研究证明了高桩码头Pushover抗震分析结果与弹塑性时程分析结果十分接近;范玉石[4]研究了能力谱法在高桩码头抗震分析中的应用;高树飞[5]分析了运用Pushover方法进行高桩码头抗震设计的实施过程;陶桂兰等[6]对比分析了不同加载模式对全直桩高桩码头抗震计算结果的影响。这些研究主要是针对沿海或长江下游的高桩码头结构,而关于长江上游或山区河流的大水位差直立式框架码头结构的静力弹塑性分析的研究较少。目前,长江上游山区河流大型码头的前沿作业平台大多数采用全直桩框架结构形式,本文以宜宾港志诚作业区一期工程的大水位差直立式框架码头结构为例,结合《建筑抗震设计规范》,采用Pushover分析方法计算分析该类型框架码头的抗震性能。
1 Pusheover分析的原理
1.1 Pushover分析的计算过程
Pushover分析的目的是对结构的抗震性能进行评价,预测结构在给定地震水平力作用下的极限反应,主要有以下4个过程[7]:(1)建立Pushover曲线;(2)选择用于评价的抗震水准;(3)选择用于评价的结构抗震性能目标。我国《建筑抗震设计规范》附录M给出了结构抗震性能目标的参考指标,大致归纳为“小震不坏、中震可修、大震不倒”的抗震性能目标[1];(4)采用特定的方法进行结构抗震性能评价[7]。目前我国主要采用能力谱法,本文即采用该方法。
1.2 能力谱法
首先通过将多自由度体系的Pushover曲线(底部剪力-顶点位移曲线)转换为等效单自由度体系的能力谱(加速度-位移),然后通过等效阻尼比βeff来评价反应谱法折减系数,将地震弹性反应谱转换为地震作用的弹塑性需求谱(加速度-位移),最后通过比较两个谱曲线,评价结构整体在弹塑性状态下的最大需求内力和变形能力,再通过与目标性能的比较,评价结构整体的抗震性能[7]。如图1所示性能状态分为三个阶段[7],图中B点为屈服点;IO点为直接使用;LS点为安全极限状态;CP点为坍塌极限状态;C点为承载力极限点;DE段为残余承载力。

图1 构件的性能评价Fig.1 Performance evaluation of components
1.3 Pushover分析的加载方式
Pushover分析中水平力的加载方式要能代表地震水平作用的惯性力,使得计算求出的构件反应结果能比较准确地反映实际地震作用的反应结果。目前,主要的加载方式有一阶振型加载、加速度加载模式、模与振型组合加载模式[8]。在计算分析过程中,根据选定的加载模式逐步增加荷载的大小,直到构件达到极限破坏状态。
2 工程实例计算
2.1 工程概况
宜宾港志城作业区位于长江三峡枢纽库尾段的宜宾市境内,一期工程建设1 000 t级多用途泊位4个、滚装泊位1个。码头前沿作业平台采用全直桩框架结构,最大水位差17.5 m,平台总长435 m,宽27.75 m,共分12个结构段。本文选取其中一个结构段进行计算分析,结构段顺水流方向长33 m,排架间距8 m,垂直水流方向宽27.75 m,桩间距8 m,共设5层系靠船平台,层高4.5 m,码头框架采用C30钢筋混凝土现浇,桩基采用灌注嵌岩桩,所有截面受力主筋采用HRB400级钢筋,箍筋采用HPB335级钢筋,主要构件截面尺寸见表1,码头前沿作业平台结构断面见图2。
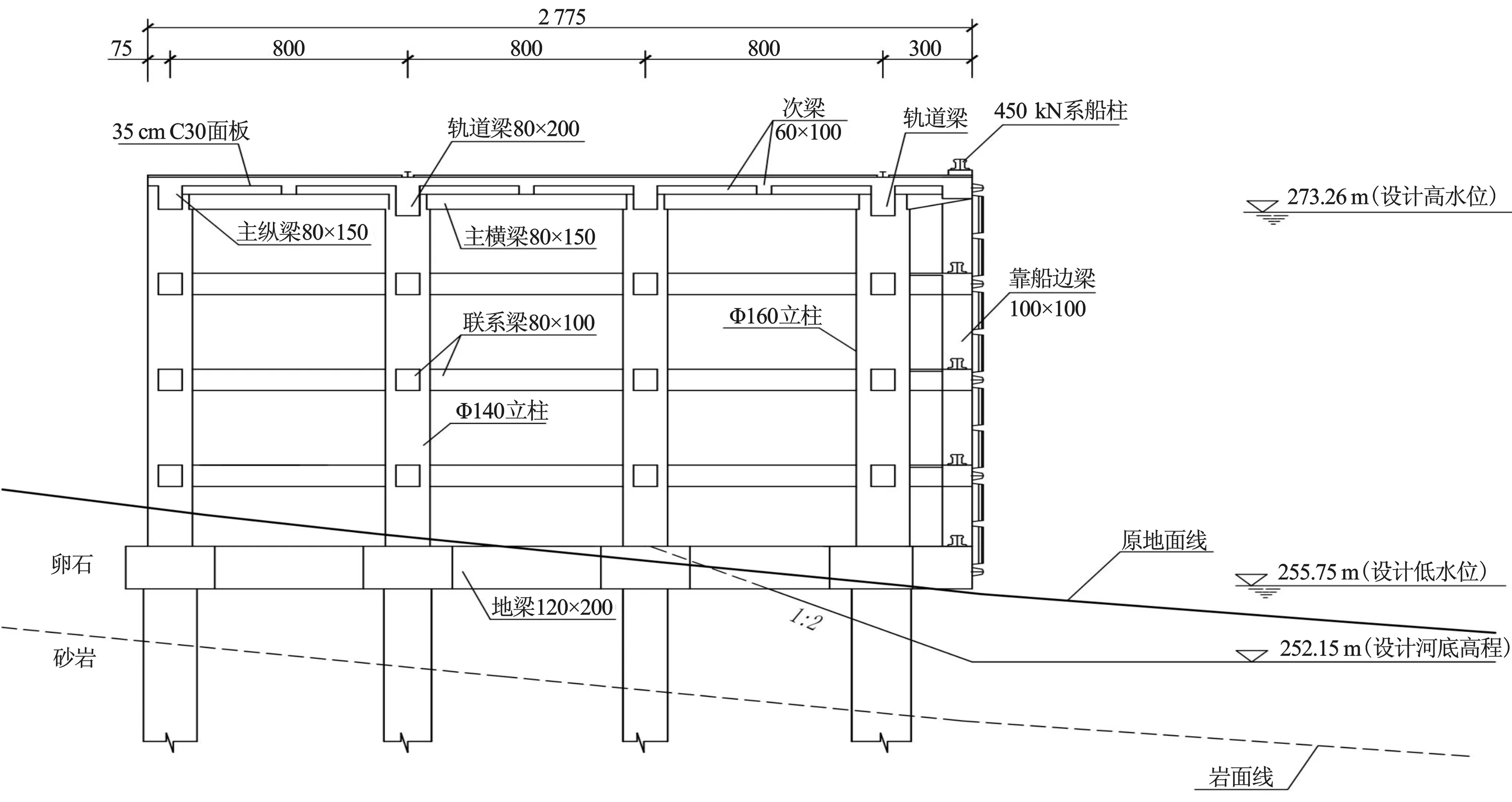
图2 码头前沿作业平台结构断面(单位:cm)Fig.2 Structural section of wharf

表1 码头结构主要构件截面尺寸Tab.1 Section size of main components
2.2 抗震水准
根据工程地质详勘报告,工程区所在区域抗震设防烈度为7度,设计基本地震加速度值及地震动峰值加速度为0.10 g,场地类型Ⅲ,设计地震分组为第一组,特征周期为Tg=0.45 s,结构常阻尼比取ξ=0.05,查询抗震设计规范可知各地震动水准下的地震影响系数最大值以及经换算后对应AT40能力谱法中的CA与CV值(表2)。
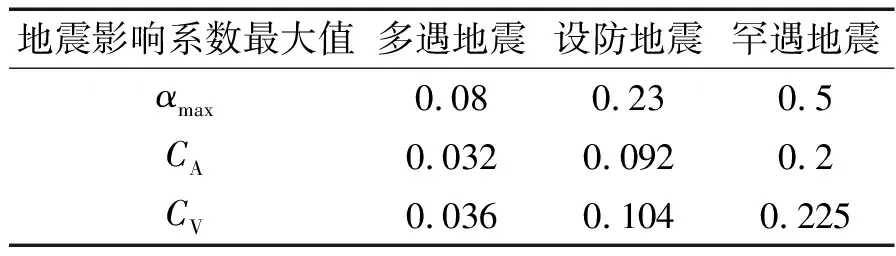
表2 地震影响系数最大值Tab.2 The maximum value of seismic influence coefficient
2.3 主要构件抗震性能目标
根据《建筑抗震设计规范》1.0.1条中“当遭受多遇地震影响时,主体结构不受损坏;当遭遇设防地震影响时,主体结构可能受损,但经一般修复可使用;当遭受罕遇地震影响时,主体结构不倒塌”的原则,码头框架主要构件抗震性能目标见表3[1]。

表3 码头框架主要构件抗震性能目标Tab.3 Seismic performance objectives of main component
2.4 计算模型
本文采用有限元软件SAP2000对码头框架结构进行Pushover计算,根据码头结构段特点建立三维空间有限元模型,码头结构下部桩基入土深度根据假想嵌固点法确定[8],计算时将嵌固点设为固结,模型中的塑性铰采用程序默认的混凝土铰属性,梁两端设置弯矩铰(M3)和剪力铰(V2),桩、柱两端设置双向压弯铰(P-M2-M3)[9]。作用于码头结构上的主要荷载有结构自重、桥式起重机荷载、系缆力和水流力。计算模型见图3,模型坐标为X轴正向垂直码头前沿线向外,Y轴正向平行码头前沿线顺水流向下,Z轴正向沿重力方向竖直向上。

图3 三维计算模型Fig.3 3D computing model
2.5 模态分析
经过模态计算分析得到码头框架结构前7阶模态的结构周期和振型质量参与系数[10](表4)。
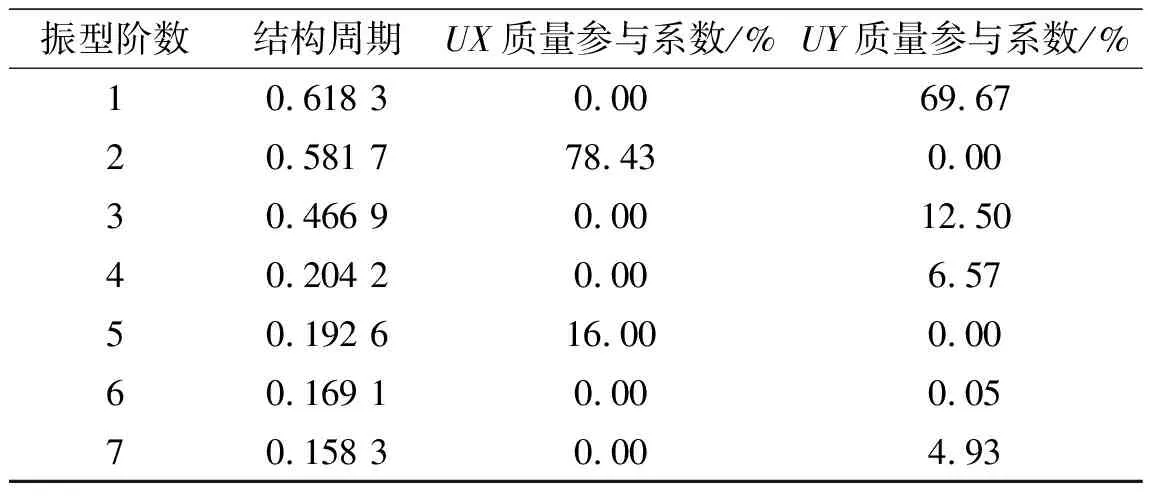
表4 结构周期及振型质量参与系数 Tab.4 Structure period and mode mass participation coefficient
从表4可以看出,结构一阶振型UY质量参与系数为69.67%,结构以Y向平动为主;二阶振型UX质量参与系数为78.43%,结构以X向平动为主。在振型组合加载方式中,X向将考虑2、5阶振型组合,Y向将考虑1、3、4、7阶振型组合。
2.6 静力推覆计算
在Pushover计算中,将计入重力二阶效应,通过三种加载方式分别在码头框架的X方向和Y方向进行加载推覆,框架结构的初始刚度将包括之前结构自重、起重机荷载和系缆力和水流力荷载产生的刚度,监测点位移选择码头平台顶面中心点的位移。三种加载方式下的码头框架底部剪力-顶点位移关系曲线见图4~图5。

图4 X向底部剪力与顶点位移关系曲线Fig.4 Relation curve between X-direction bottom shear and vertex displacement图5 Y向底部剪力-顶点位移关系曲线Fig.5 Relation curve between Y-direction bottom shear and vertex displacement
从图4、图5中可以看出,三种加载方式下得到的曲线基本一致,一阶振型加载得到的曲线斜率略小于另两种加载方式,主要因为X向二阶振型质量参与系数为78.4%,Y向一阶振型质量参与系数为69.7%,框架结构的总地震反应以低阶振型反应为主,一阶振型加载主要考虑低阶振型对框架结构影响,而振型组合加载考虑了高阶振型的影响,加速度加载未考虑振型的影响,因此加速度加载的曲线斜率最大,一阶振型加载的曲线斜率最小。振型组合与加速度两种加载方式得到的曲线相当接近,整体框架结构达到目标位移时,X向最大推覆力为29 489 kN,Y向最大推覆力为30 343 kN,最大侧向力取三种加载方式的均值。总体来看,框架结构平面两个方向上的刚度十分接近,Y向刚度略大。
2.7 抗震性能估计
(1)码头框架结构整体抗震性能估计。
选用SAP2000中ATC-40能力谱法[9],根据表2中的系数CA与CV值绘制各级地震水准下的需求谱曲线,并通过比较结构能力谱与需求谱曲线得到结构体系的性能点,本文将罕遇地震下的性能点值列于表5。

表5 性能点处的底部剪力和顶点位移Tab.5 Bottom shear and vertex displacement at performance point
从表5可以看出,三种加载方式下X向和Y向的底部剪力和顶点位移相差不大,Y向底部剪力略大于X向底部剪力,表明码头框架结构在罕遇地震作用下两个方向的抗震性能比较接近。在罕遇地震作用下,性能点处X向最大侧向力为22 990 kN(取三者均值),小于目标位移处的最大侧向力29 489 kN,Y向最大侧向力为25 912 kN(取三者均值),小于目标位移处的最大侧向力30 343 kN,表明码头框架结构在平面两方向均满足大震不倒的要求。
通过计算,码头框架结构在3种侧向加载方式下,最大侧向力对应的弹塑性层间位移见图6~图7。

图6 X向层间位移角变化曲线Fig.6 Variation curve of X-direction inter-story displacement angle图7 Y向层间位移角变化曲线Fig.7 Variation curve of Y-direction inter-story displacement angle
从图中可以看出,三种加载方式下X向和Y向的层间位移角曲线比较接近。码头框架结构在最大侧向力作用下,X向最大层间位移角在第二层,其值为11/6 000(取三者均值),Y向最大层间位移角在第三层,其值为13/6 800(取三者均值);进入塑性阶段后,码头框架结构第二、三层比较薄弱,但两者的层间位移角均小于1/50,满足《建筑抗震设计规范》要求罕遇地震下弹塑性层间位移角要求。
(2)码头框架主要构件性能估计。
为与设定的抗震性能目标进行比较,对主要构件塑性铰进行了数据统计(表6)。

表6 主要构件塑性铰统计表Tab.6 Statistical table of plastic hinge of main components
由表6塑性铰的统计数据来看,构件在多遇地震作用下完全处于弹性阶段;在设防地震作用下,联系梁、地梁和靠船构件65%以上和少数桩基和立柱出现塑性铰,但均处于直接使用阶段状态;在罕遇地震作用下,桩基和立柱72%以上塑性铰处于安全极限状态,地梁、联系梁和靠船构件96%以上塑性铰处于坍塌极限状态,这样可以有效地消耗地震能量,使码头框架结构在竖向处于稳定。从码头框架主要构件塑性铰的演变过程来看,三种侧向加载方式的计算结果基本一致,X向加载下构件的塑性铰最早出现在框架后排桩基底部,随后塑性铰依次出现在第三排、第二排、第一排、横向联系梁、立柱、横梁两端,其中第一排桩基底端塑性铰在其余几排桩基、底部两层联系梁出现塑性铰之后才出现,而桩基顶部在达到目标位移后未出现塑性铰,确保了码头框架结构在达到目标位移后的竖向稳定。Y向塑性铰最先出现在前排桩基底部,然后依次沿后排桩基、地梁、联系梁、立柱纵梁出现塑性铰,达到目标位移时,除前排桩基部分塑性铰处于安全极限状态,其余处于直接使用阶段,因此结构竖向仍然稳定。
3 结语
结合《建筑抗震设计规范》中基于性能的抗震设计要求,本文采用静力弹塑性分析方法,通过SAP2000有限元计算软件,对山区河流大水位差直立式框架码头结构进行了抗震性能计算分析。计算结果表明:三种侧向加载方式的计算结果基本一致,X向加载下构件的塑性铰最早出现在框架后排桩基底部,Y向塑性铰最先出现在前排桩基底部,而桩基顶部在达到目标位移后未出现塑性铰,确保了码头框架结构在达到目标位移后的竖向稳定,因此该种框架结构形式完全满足“小震不坏、中震可修、大震不倒”的抗震设防目标,在罕遇地震作用下,码头框架结构柱之间的联系梁、地梁首先进入塑性破坏,可以起到消耗地震能量的作用,能有效地保证码头框架结构整体的竖向稳定,侧向加载至破坏的整个过程属于延性破坏,符合框架结构“强柱弱梁”的抗震设计理念。最后,希望本文工程实例的计算分析过程和结论对类似工程结构的抗震分析起到抛砖引玉的作用。

