新疆托克逊县乌斯通沟水库土石坝三维有限元计算分析

柴 扬

（吐鲁番市清源水利水电勘测设计院有限公司,新疆 吐鲁番 838000）

1 概况

乌斯通沟水库属新疆维吾尔自治区吐鲁番市托克逊县。乌鲁木齐以南162 km 处；吐鲁番以西51 km,与吐鲁番市为邻。乌斯通沟水库主要任务是解决灌溉用水和工业园区供水问题,是一座具有综合效益的水库枢纽工程。主要建筑物由沥青砼心墙砂砾石坝﹑左岸灌溉放水洞、右岸溢洪洞、导流冲砂兼放空洞组成。水库总库容1440/1130 万m3,拦河坝坝高73.0 m。工程等别为Ⅲ等,工程规模为中型水库。根据《水利水电工程等级划分及洪水标准》（SL 252-2017）4.2.2 条规定,3 级建筑物的土石坝坝高超过70 m 时,大坝建筑物级别可提高一级,洪水标准可不提高,本工程大坝坝高为73.0 m,因此,本工程大坝级别提高为2 级建筑物。大坝溢洪洞、灌溉放水洞、导流兼放空冲砂洞等主要建筑物为3 级建筑物；次要建筑物为4 级建筑物；临时建筑物为5 级建筑物。建筑物边坡级别为3～5 级,公路等级为4 级,桥涵等级为4 级,汽车荷载按公路-Ⅱ设计。

2 分析计算的目的

对坝体进行了三维有限元静动力计算,研究了坝体的应力应变规律。

主要目的有：（1）通过计算大坝在蓄水期内的沉降、水平位移分布、最大主应力、应力分布、最小主应力等；（2）在大坝遇到地震时,大坝的坝顶加速度、坝顶放大系数以及地震后的残余变形等[1～2]。

3 大坝边坡稳定分析计算

3.1 计算模型

3.1.1 静力本构模型

静力本构模型通过三轴试验,能快速、明了的反映土体应力应变的非线性特征。其中切线弹性模量表达式为 ：

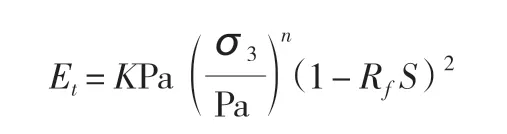
式中：Et为切线弹性模量；K 为初始模量基数；Rf为破坏比参数；Pa 为大气压力。

静力本构模型通过三轴试验,同时能够快速、明确地反映出土体应力应变的非线性特征。其中切线弹性模量表达式为

切线泊松比为：

反映材料强度发挥程度,表达式为：

由于邓肯E-υ 模型是针对二维问题提出的,在三维计算中,根据广义剪应力q 代替（σ1-σ3）,以平均主应力p 代替σ3,将其推广到三维问题。

破坏偏应力（σ1-σ3）f 则根据三维问题的摩尔-库仑准则[4],表示为：

上述各式中,Pa 为单位大气压力,C、φ0、Δφ、K、n、Rf、D、F、G、Kur、nur为模型参数,由常规三轴试验得出。

3.1.2 动力本构模型

堆石坝在遇到地震时,地震的震动会使大坝更为密实,同时会使大坝在遇到后面的震动破坏时防御力明显加强[5]。

在计算有效主应力与最大动剪模量用下方公式拟合：

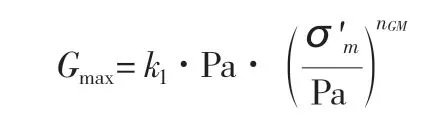
式中：Pa 为大气压力；k1、nGM为试验参数；σ'm为平均有效主应力。

为考虑初始围压的影响,对动剪应变γd进行归一化处理：

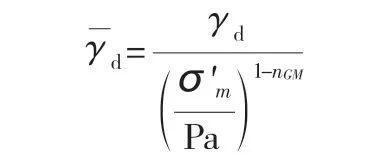
G/Gmax与归一后动剪应变的关系,式中k2为试验参数：

下式中k3为试验参数：

3.2 计算公式

（1）静力平衡计算公式

静力平衡方程:[K]{δ}={R}

堆石体变形主要与荷载、时间、加载方式有着密切关系[5]。

（2）静力平衡计算公式

根据现在已有相关研究成果,基岩上的100 m 级面板堆石坝,动水压力对大坝的影响较小,本次不考虑动水压力的影响。则动力平衡公式为：

式中：Gi和分别为单元第i 次迭代计算时的动剪模量和阻尼比,ε值在10%左右。

（3）遇到地震活动后大坝永久变形计算公式

地震活动过程中的残余应变：

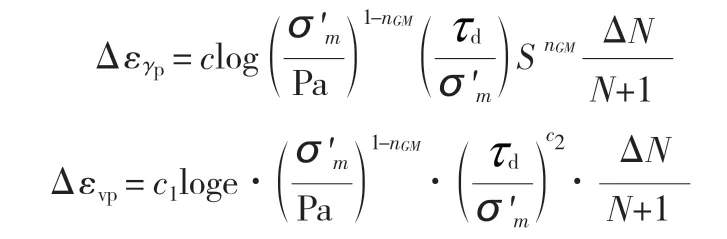
式中：Δεγp为残余剪切应变,Δεvp为残余体积应变,Pa 为大气压力；为平均有效主应力；k1、k2、k3、nGM、n1为试验参数。

依据流动法则,将残余应变换算成直角坐标系下的应变：

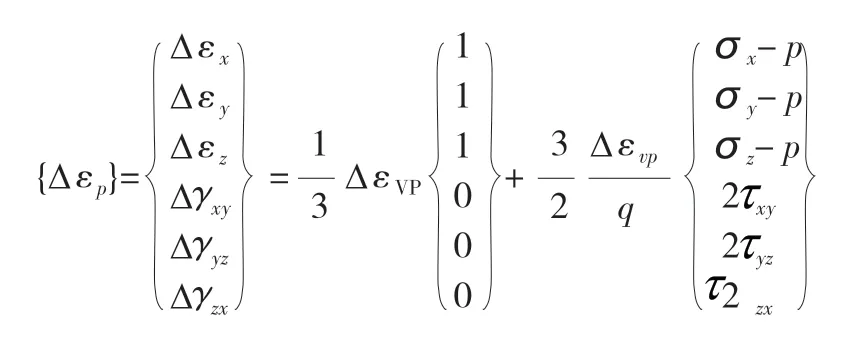
式中：p 为平均主应力；q 为广义剪应力。

则等效结点力为：

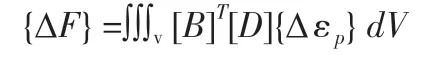
式中：[B]为应变转换矩阵；{∆εp}为直角坐标系下的残余应变增量；[D]为弹性矩阵。

进行静力有限元分析时,要将计算得到的等效节点力作用到坝体上。所得的变形即为地震永久变形。

3.3 坝体填筑及蓄水加载

大坝三维结构有限元计算加载过程见表1,共分23 级模拟整个坝体加载及蓄水过程。

表1 大坝加载过程分级明细表

3.4 计算工况

（1）静力参数

本次计算静力计算参数见表2。

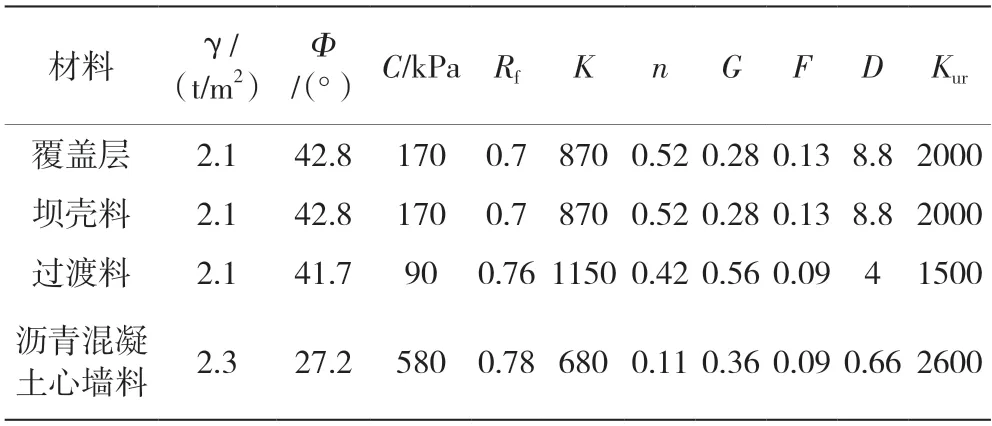
表2 乌斯通沟模型计算参数

（2）动力参数

乌斯通沟沥青心墙坝坝料动力系统参数,通过进行类比已有的土石坝坝料试验结果,综合考虑坝料的设计干密度以及母岩岩性等情况最终确定。

表3 坝料动力计算参数表

3.5 坝体有限元计算网络剖分

采用典型河床剖面自动划分坝体单元,见图1、图2,设置43 个计算剖面在沿坝轴线方向,坝轴线方向的长度与图中横向轴保持一致；Z 轴方向按照左岸负、右岸正的原则；X轴方向按照向上游正、向下游负；Y 轴方向按照向下负、向上正的原则[5]。

图1 典型剖面网格立视图

图2 典型剖面网格剖分图（0+137 剖面）

4 计算结果及分析

通过对乌斯通沟土石坝的三维有限元静动力计算成果与实际情况比较分析,成果与实际情况基本一致,结果合理,计算结果见表4。

表4 不同工况下大坝动力反应及永久变形计算结果

由表4 可知；

（1）对大坝可以进行三维地震反应分析,最大加速度反应的放大倍数约2.6 倍,其位置基本在坝顶部位,存在鞭稍效应。最大沉降发生在坝高的1/2 处（完工期和蓄水期）,坝体的最大竖直方向位移和沉降均占小于坝高的1%。

（2）最大沉降发生在坝高的1/2 处（完工期和蓄水期）,坝体的最大竖直方向位移和沉降均占小于坝高的1%。

5 结语

通过乌斯通沟水库的建设实例,可以看出通过计算分析,我们不仅可以掌握大坝在正常工况下的坝体沉降、水平位移、防渗墙应力、变形；而且还能掌握在大坝遇到地震时的震后的残余变形等重要参数,经过对土石坝三维有限元计算分析,可为今后优化类似工程和减少工程投资等提供依据。