船载测控天线的引导数据处理方法
张 凤
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
船载伺服设备在海上接收到中心计算机发送的引导数据(引导数据是1Hz或者20Hz),用于引导天线进行捕获跟踪目标,由于离中心距离较远,造成了数据传输引导的延时,如果直接映射到伺服设备上就会造成很大的误差,所以必须对引导数据进行处理。
1Hz的引导数据不能直接外推到当前时间直接用于引导,1Hz的数据采样率太低,对于高速目标来说,将引导数据进行外推到当前时间用于伺服捕获目标精度太差,不能满足跟踪要求。因此提出了将引导数据先用拉格朗日插值成20Hz的数据再进行外推就可以满足跟踪要求。
1 引导数据
对于动态目标来说,可以预先知道其动态飞行轨迹。这些动态数据通过上级设备转发后最终通过中心计算机转发到伺服设备,数据源里面的时间T并不是真正的飞行时间,只是一个相对时间,因此需要根据目标的起飞时间,然后根据拉格朗日插值插成50ms的数据,再外推到当前时间的数据用于伺服跟踪。基于数据类型可以分为地心坐标系(如图1),数据格式XYZ形式,以及地平坐标系,如图2。从图1和图2 可以看出,地心坐标系到地平坐标系存在一种转换方式[1]。不同的数据格式数据处理的方式也不相同。
图1 地心坐标系
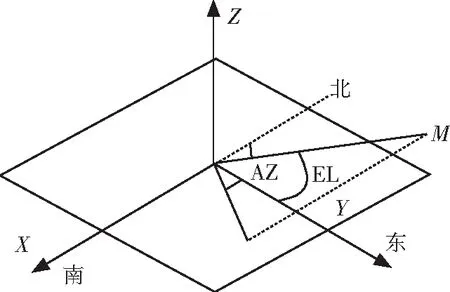
图2 地平坐标系 M点为目标;AZ为方位角,表示空间M点到地平面映射点与正北夹角;EL为俯仰角,表示空间M点与正东的夹角。
2 方位俯仰引导原理
基于上级数据来源为方位地理角俯仰地理角的数据格式,数据周期如果为1Hz,这种数据格式在固定站的测控天线引导中有较多的应用,船载移动站中使用较少,船载测控天线随着船的航向,载体的姿态、位置一直处于动态变化中,如果直接用于天线引导,姿态数据的变化将会影响指向精度,在固定站或者船载移动站中为了使天线可以平稳地工作,需要将1Hz的数据进行预处理插值成20Hz的数据。拉格朗日插值算法可以反映数据内在规律,因此对角度数据的处理采用拉格朗日插值再进行数据外推。
2.1 拉格朗日插值原理[2]
从收到的数据中选取相邻的3个数据点:t0、t1和t2,对应的数据值为y0、y1和y2,相邻三个数据点的时间差为1s
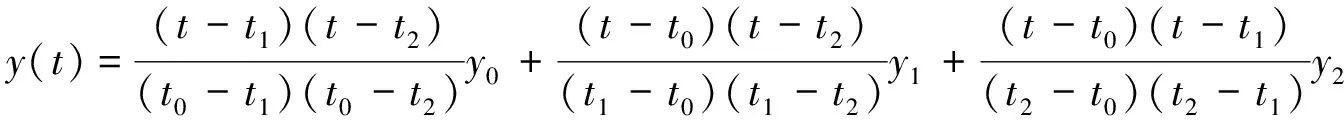
(1)
根据公式(1)插值成50ms,
t=t0+n·Δt(n=0,1,2…19)
(2)
以n为变量将公式(1)简化为公式(3):
y(n)=[(0.0354n)2+0.075(0.0354n)+1]y0+[0.05n(2-0.05n)]y1+0.025n×(0.05n-1)y2
(3)
2.2 引导外推数据处理
由公式(3)得到相邻50ms的数据点,将此数据进行外推得到当前时间T的数据点y(T),K为线性外推的斜率值。
K=y(n)-y(n-1)
(4)
y(T)=(T-n)×K+y(n)
(5)
2.3 引导数据对齐处理
天线随着载体姿态的变化,跟随引导数据指向时,为保证精准引导,姿态的数据也需要具备实时性,惯导设备与引导数据输出设备以及伺服设备都需要用同一个时间,因此还需要将引导数据的时间和姿态的时间对齐。实际情况中,姿态数据是100Hz的,伺服环路控制也是100Hz,因此需要将20Hz的引导数据再次按拉格朗日插值原理插值成100Hz的数据,然后直接用于伺服环路输入进行伺服引导。
3 XYZ引导原理
如果目标运动速度快,短时间内位置变化快,数据传输到伺服设备这段时间为目标当前的位置信息、载体的姿态信息较采集到数据时的数据值已经改变,如果再用这个数据用于引导,天线将会偏离目标,偏离目标的差值越大,造成的误差越大,在此情况下直接采用XYZ引导数据格式外推将会避免载体姿态的影响,降低传输时间延时造成的误差。将收到的XYZ数据外推到当前时刻,根据此时载体的位置信息转换成方位俯仰地理角,用于引导捕获。
3.1 XYZ格式数据处理
基于XYZ数据的规律,通过数据分析发现XYZ数据格式下X、Y、Z三个分量几乎成线性分布,因此将预测时刻的XYZ格式数据中的X、Y、Z分量分别进行线性外推,得到当前时刻的XYZ数据,结合惯导的当前位置信息和姿态信息,再根据坐标变换转为方位俯仰引导角度,用于引导天线跟踪目标。引导数据下发到控制器的时间为20Hz,因此以20Hz的周期为基准,T1,T2,为相邻周期的两个时刻,对应的数据分别为X1,Y1,Z1,X2,Y2,Z2,当前时刻为T,对应的数据分别为X,Y,Z。根据T1,T2两个时刻的数据X1,Y1,Z1,X2,Y2,Z2,线性外推到当前时刻T的数据X,Y,Z,KX,KY,KZ分别为XYZ数据的斜率,根据斜率值和时间差计算得到当前时刻的数据:
KX=(X2-X1)/(T2-T1)
X=X2+KX × (T-T1)/50
KY=(Y2-Y1)/(T2-T1)
Y=Y2+KY×(T-T1)/50
KZ=(Z2-Z1)/(T2-T1)
Z=Z2+KZ×(T-T1)/50
3.2 XYZ数据转换处理
通过原始数据外推得到当前时刻的XYZ数据为地心坐标系下的数据值,天线引导最终需要的是地平坐标系下的地理角度,因此XYZ数据还不能直接用于捕获引导,需要将XYZ数据结合惯导的当前位置、姿态信息进行坐标变换转化成方位俯仰地理角才能用于控制器引导。
XYZ数据格式转换成角度代码计算如下:
f_latitude为本地经度单位为弧度,f_latitude为本地纬度单位为弧度,X为XYZ数据格式中X分量值,Y为XYZ数据格式中Y分量值,Z为XYZ数据格式中Z分量值,re0为地球半径,PI为圆周率,f_l为固定值1/298.257222,f_heigh为当前位置的高度单位为m,AZ为方位地理角单位为°,EL为俯仰地理角单位为°。
g1、g2 、f_xg、f_yg、f_zg、xh、yh、zh、f_x、f_yg、f_z均为临时变量;
g1=re0/sqrt(1-(2*f_l-f_l*f_l)*sin(f_latitude)*sin(f_latitude))+f_height;
g2=re0*(1-f_l)*(1-f_l)/sqrt(1-(2*f_l-f_l*f_l)*in(f_latitude)*sin(f_latitude))+f_height;
f_xg=g1*cos(f_latitude)*cos(f_longitude);
f_yg=g1*cos(f_latitude)*sin(f_longitude);
f_zg=g2*sin(f_latitude);
f_x=X-f_xg;
f_y=Y-f_yg;
f_z=Z-f_zg;
m_dR=sqrt(f_x*f_x+f_y*f_y+f_z*f_z);xh=-(-sin-(f_latitude)*-cos-(f_longitude)*f_x+-sin-(f_latitude)*-sin-(f_longitude)*f_y--cos-(f_latitude)*f_z);
yh=-(-sin-(f_longitude)*f_x--cos-(f_longitude)*f_y);
zh=-cos-(f_latitude)*-cos-(f_longitude)*f_x+-cos-(f_latitude)*-sin-(f_longitude)*f_y+-sin-(f_latitude)*f_z;
AZ=atan(yh/xh);
AZ=AZ*180.0/PI;
EL=atan(sin(AZ*PI/180.0)*zh/yh);
EL=EL*180.0/PI;
4 结 论
测控天线通过接收引导数据指向目标,为天线快速捕获目标提供了可靠的保障,因此对引导数据的处理算法直接决定了测控天线引导过程是否快速、平稳、准确。本文中讲述了两种数据格式的处理方法,地平系数据格式的地理角度拉格朗日插值算法与地心坐标系下的XYZ数据格式的线性外推的算法的,这两种算法适用于不同的载体环境,前者适用于固定站即天线位置固定,XYZ数据格式固定站与动中测都可以,在不同的载体环境下选择相应的算法完全可以实现测控天线精准平稳引导,并在测控天线的应用实践中得到了充分的验证,从而实现了理论的实际应用。

