考虑延时的孤岛微电网频率协同控制策略稳定性分析及改进

李志军，张牟发，张家安

考虑延时的孤岛微电网频率协同控制策略稳定性分析及改进

李志军1, 2，张牟发3，张家安1, 2

(1. 河北工业大学省部共建电工装备可靠性与智能化国家重点实验室，天津 300130；2. 河北工业大学河北省电磁场与电器可靠性重点实验室，天津 300130；3. 河北工业大学人工智能与数据科学学院，天津 300130)

孤岛微电网中广泛使用下垂控制，其在负荷变化后会导致系统稳态频率偏离额定值. 而传统集中式二次控制方法存在可靠性低、可拓展性不足等问题. 基于分布式协同控制原理，设计了一种频率二次协同控制策略，以克服传统集中式二次控制的缺陷，使系统频率恢复到额定值. 考虑到孤岛微电网系统内分布式电源之间通信条件限制和实际过程中数字电路采集时滞等因素造成的控制延时和通信延时，利用盖尔圆盘定理和奈奎斯特稳定判据分析了延时对频率二次协同控制策略稳定性造成的影响，提出一种计算控制延时临界值的方法，判断控制延时影响下的协同控制系统稳定性；针对控制延时对稳定性的影响，改进了频率二次协同控制策略，并给出了改进型协同控制策略的稳定性分析过程和参数设计方法；改进后的策略可以保证系统在更大的控制延时下稳定运行；最后通过Matlab/Simulink搭建了所研究的微电网的仿真模型. 仿真结果表明：基于分布式协同控制原理设计的频率二次协同控制策略可以实现孤岛微电网系统的频率恢复；控制延时会影响分布式协同控制系统的稳定性，控制延时超出临界值会造成控制系统失稳. 通过改进频率二次协同控制策略，可以提升分布式协同控制系统的稳定裕度，使其在更大的控制延时范围内保证微电网稳定运行.

孤岛微电网；频率二次控制；协同控制；控制延时

近年来，以风电、光伏为代表的可再生能源在电力系统中的占比持续增加．由于可再生能源存在间歇性和波动性等特点，其直接接入电网会对电力系统安全性和电能质量造成不良影响．为解决这一问题，微电网(microgrid，MG)的概念应运而生．微电网是由分布式电源(distribute generation，DG)、储能设备、负载和相关的保护与控制设备组成的小型电力系 统[1]．其作为可再生能源消纳问题的一种重要解决方案，近年来受到人们越来越多的关注．

微电网具有两种运行模式：并网模式和孤岛模式[2]．当微电网工作在孤岛模式下时，由于缺少大电网支撑，需要微电网自身提供频率和电压支撑．在孤岛微电网中，为保证系统稳定运行和合理分配有功，参与调频的分布式电源普遍采用下垂控制[3]，下垂控制为有差调节手段，可能会在负荷变化较大时造成微电网频率的稳态误差超限[4]，影响电能质量．为解决此问题，研究者提出频率二次控制策略并将其运用到微电网频率控制中[5]．传统频率二次控制多采用集中式控制，利用微电网中央控制器(microgrid central controller，MGCC)和集中通信系统，采集各节点的信息，将信息计算处理得到的调节指令反馈给各分布式电源实现二次调频控制．集中式控制由于高度依赖全局通信和中央控制器，因此存在可靠性低、经济性差、可拓展性不足等诸多问题[6-7]．

为克服集中式控制的缺陷，研究者提出了分布式协同控制策略，并用于孤岛微电网频率二次控制[8-10].文献[8]提出了一种利用分布式协同控制的频率二次控制策略，通过使用事件触发的方法来减少控制器更新的次数，以有限的计算资源来补偿孤岛微电网中下垂控制产生的偏差来实现频率恢复．文献[9]提出了一种分布式固定时间二次协同控制方法来实现频率的无差控制．文献[10]提出了一种新颖的基于自适应协同共识原理的电压和频率控制策略，以补偿电压和频率偏差，并消除传感器和执行器故障的负面影响．上述采用的分布式协同控制皆是在理想条件下进行，并未考虑实际运行过程中因通信条件(如通信带宽)限制而存在的通信延时和对数据采集、运算处理而产生的控制延时．而在实际运行的微电网系统中，这两种延时都会对微电网协同控制策略造成消极影响[11]，影响控制品质．

针对延时对协同控制策略的影响，文献[12]利用分布式电源间的分布式通信网络，提出了一种基于分布式协同控制的自适应下垂控制策略，用于解决传统下垂控制存在稳态误差的问题，并分析了通信延时对系统控制策略的影响．文献[13]提出了一种新型的基于随机共识的孤岛微电网二次电压和频率恢复方案，考虑了通信延迟和噪声造成的消极影响，并利用李雅普诺夫方法证明了所提方法的稳定性．文献[14]利用分布式协同一致性理论提出了一种频率和电压的恢复控制算法，能实现最优的有功分配以及精确的无功分配．并考虑通信延时造成的影响，得出通信延时不影响系统稳定性的结论．文献[15]将非线性DG动力学模型转换为一阶线性模型之后，在频率恢复中引入了分布式比例积分算法，该算法可以适应通信延时等各种不确定性．文献[16]利用分布式协同控制算法，设计了频率和电压恢复控制策略，分析了时变延时对策略稳定性的影响．上述分布式协同控制的研究对延时造成的影响进行了初步分析，得出了通信延时并不影响协同控制系统稳定性的结论．但由于其仅仅考虑了通信延时，忽略了对控制延时影响的分析和讨论．此外，也未给出针对延时的具体改进措施．

基于上述问题，本文首先基于分布式协同控制原理设计了频率二次协同控制策略；然后，通过分析延时对协同控制策略稳定策略稳定性的影响，给出了一种计算控制延时临界值的方法．在此基础上，对所设计的频率协同控制策略进行改进，并对改进后的控制策略进行了稳定性分析，给出了改进型策略的参数设计方法．最后通过仿真验证了本文分析的正确性和所提控制策略以及改进措施的有效性．

1 基于分布式协同控制原理的频率二次控制策略设计

针对传统集中式频率二次控制方法存在可靠性低、可拓展性差等缺陷，本文基于分布式协同控制原理设计了频率二次协同控制策略，利用本地信息和邻边信息，在本地控制器实现频率的无差控制．

1.1 分布式协同控制原理

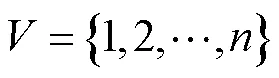
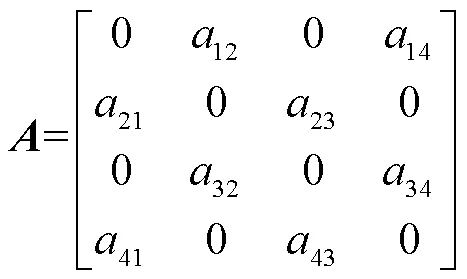
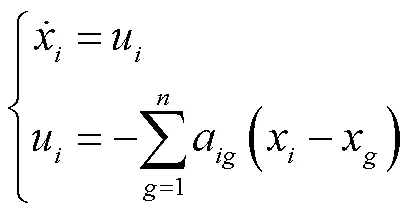
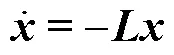
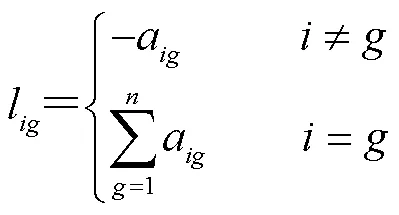
可以证明，若通信拓扑是连通的，则拉普拉斯矩阵为半正定矩阵，上述系统中的所有节点将收敛到相同的值[17-18]．

1.2 孤岛微电网频率二次协同控制策略设计

孤岛微电网频率二次控制是负荷变化后，在一次下垂控制的基础上通过修改有功功率给定值实现下垂曲线平移，实现频率的恢复．

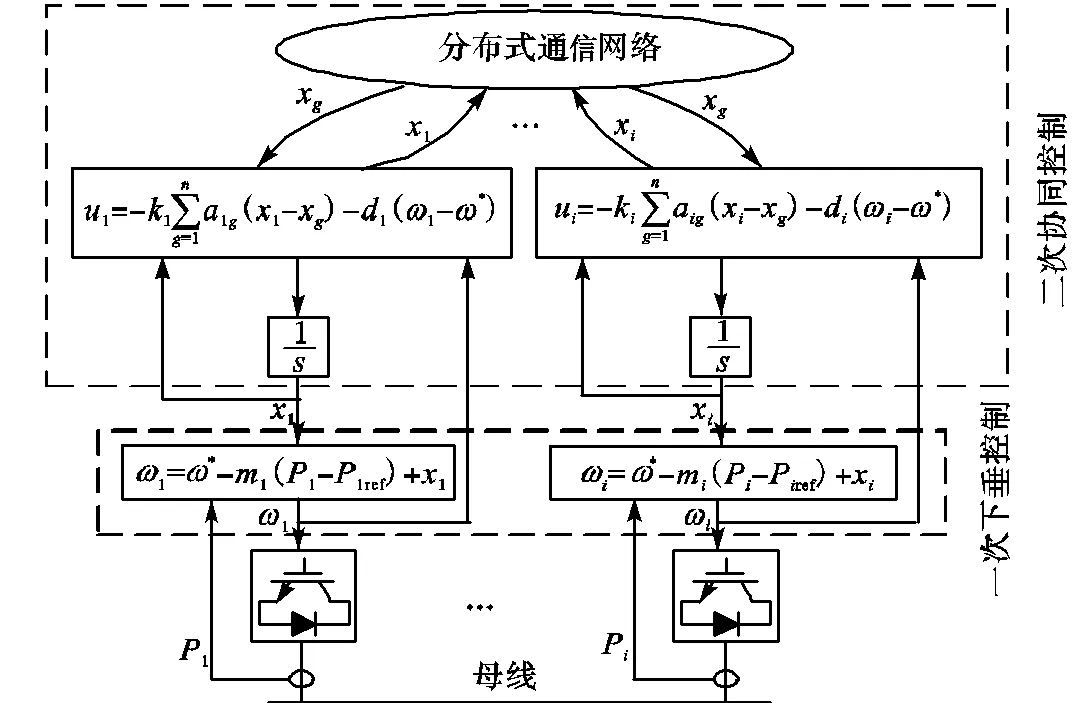
图2 微电网频率二次协同控制策略示意

以图2中的DG为例，一、二次控制结合的表达式为

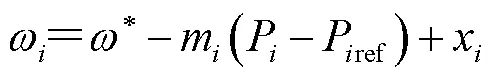
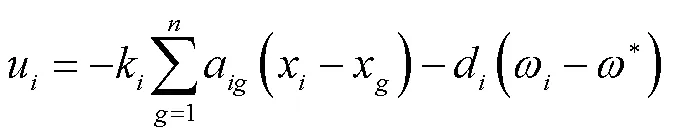
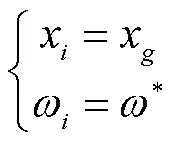
图3 一、二次控制原理

Fig.3 Principle of primary control and secondary control

2 延时对频率协同控制策略的影响

2.1 延时的数学表达

在式(4)和式(5)所示的控制策略作用下，孤岛微电网可以实现频率的恢复和有功的合理分配．但式(5)是在理想条件下设计的控制策略，并未考虑到实际过程中存在的延时．在微电网协同控制中，主要受两类延时的影响：第1类是节点间传输数据受通信链路等因素的限制而产生的通信延时，第2类是节点自身对数据的运算处理产生的控制延时．针对延时中的控制延时和通信延时，其在频率二次协同控制策略中的数学表达式为

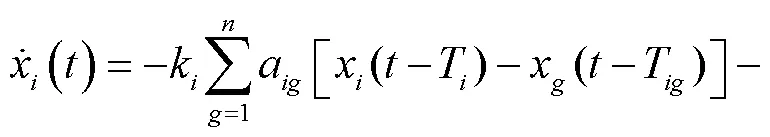
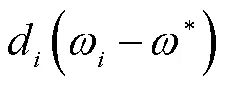
2.2 控制延时影响分析

微电网协同控制系统稳定性与传递函数的零极点分布紧密相关，因此分析延时对零极点的影响即可．对式(8)进行拉普拉斯变换可得

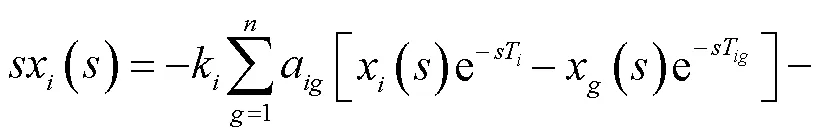
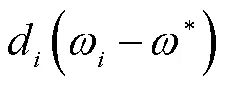
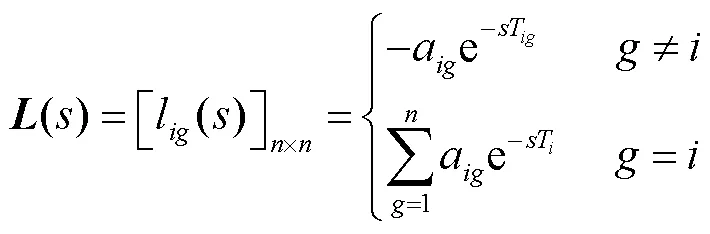
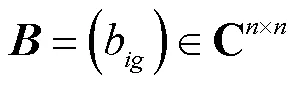
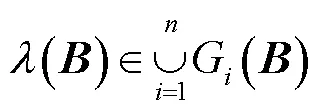
矩阵的盖尔圆表达式为

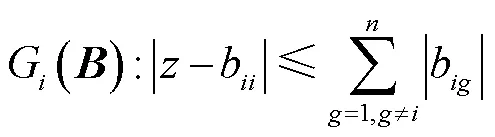
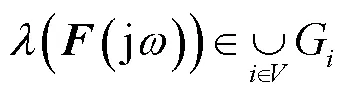
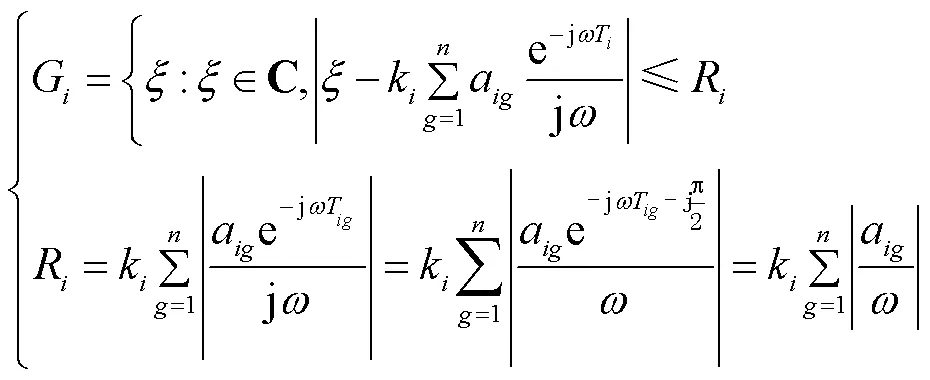
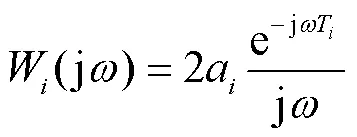
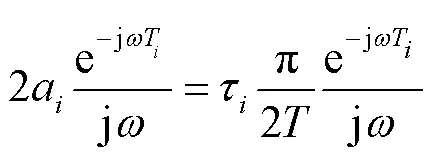
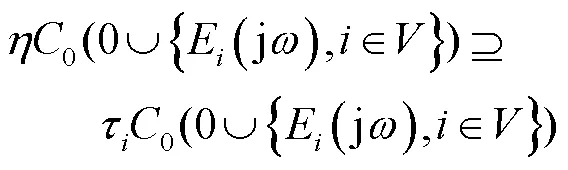
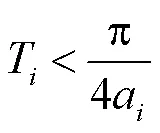
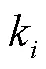
3 频率二次协同控制策略的改进

3.1 考虑延时的协同控制策略的改进

在第2.2节的分析指出，控制延时会影响协同控制策略稳定性．在工程实践中，对有较大惯性或滞后的被控对象，常用比例微分控制器来改善系统动态特性[21-26]．因为微分作用与偏差变化率成比例，即它是根据偏差变化趋势产生控制作用，因而有预先控制的性质，起到超前调节的作用．受此启发，本文为减小控制延时造成的不良影响，改善协同控制系统性能，在式(8)的基础上，对所设计的频率二次协同控制策略进行改进，改进公式为

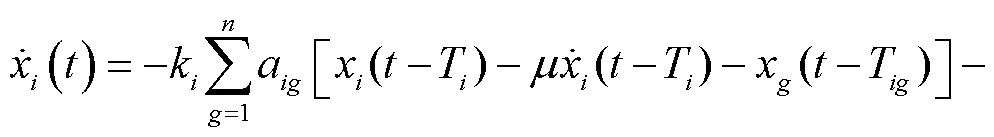
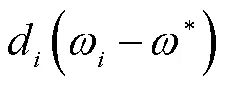
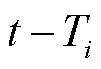
3.2 改进后的控制策略稳定性分析

与第2.2节中分析过程类似，对式(19)进行拉普拉斯变换可得

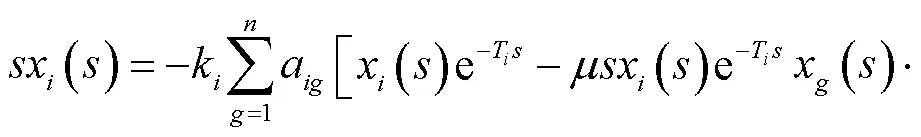
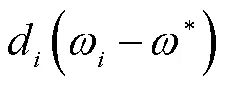
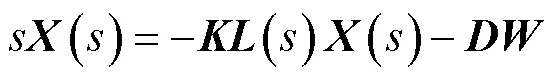
根据式(20)，可得式(21)中矩阵()元素l为

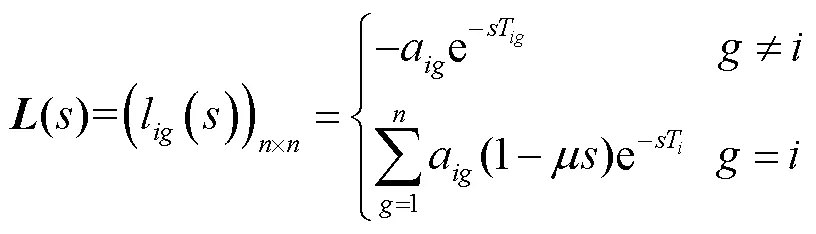
式中：a为邻接矩阵中的元素；T为控制延时；T为通信延时；为改进项中的微分系数．因此可得式(19)的特征方程为

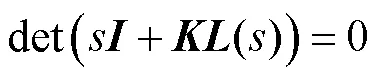
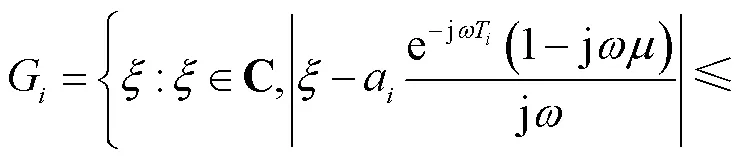
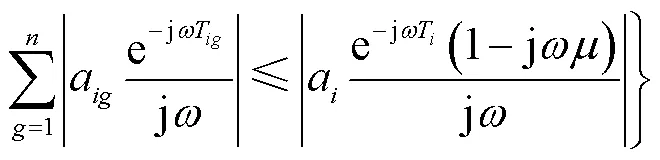
则盖尔圆的圆心表达式为

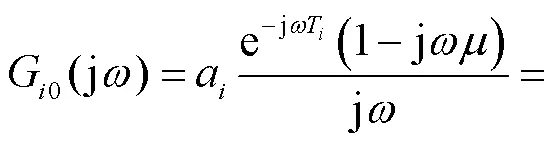
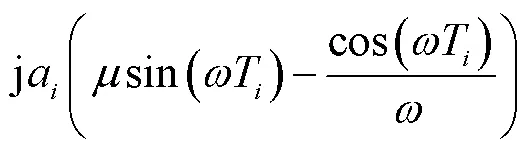
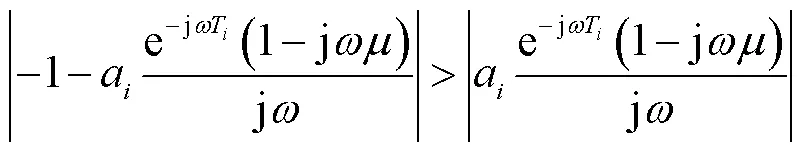
对式(26)进行整理可得

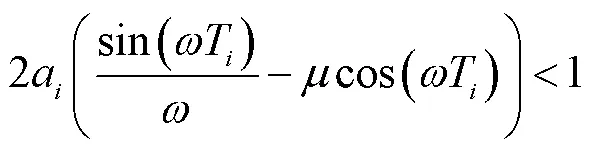
4 仿真结果及分析

为了验证本文所提频率二次协同控制策略和改进措施的有效性以及相关分析的正确性，在Matlab/Simulink仿真平台上搭建了如图4(a)所示的带有4个分布式电源的孤岛微电网仿真系统．模型中分布式电源之间的通信拓扑如图4(b)所示．本文仿真系统所使用的具体参数如表1和表2所示．

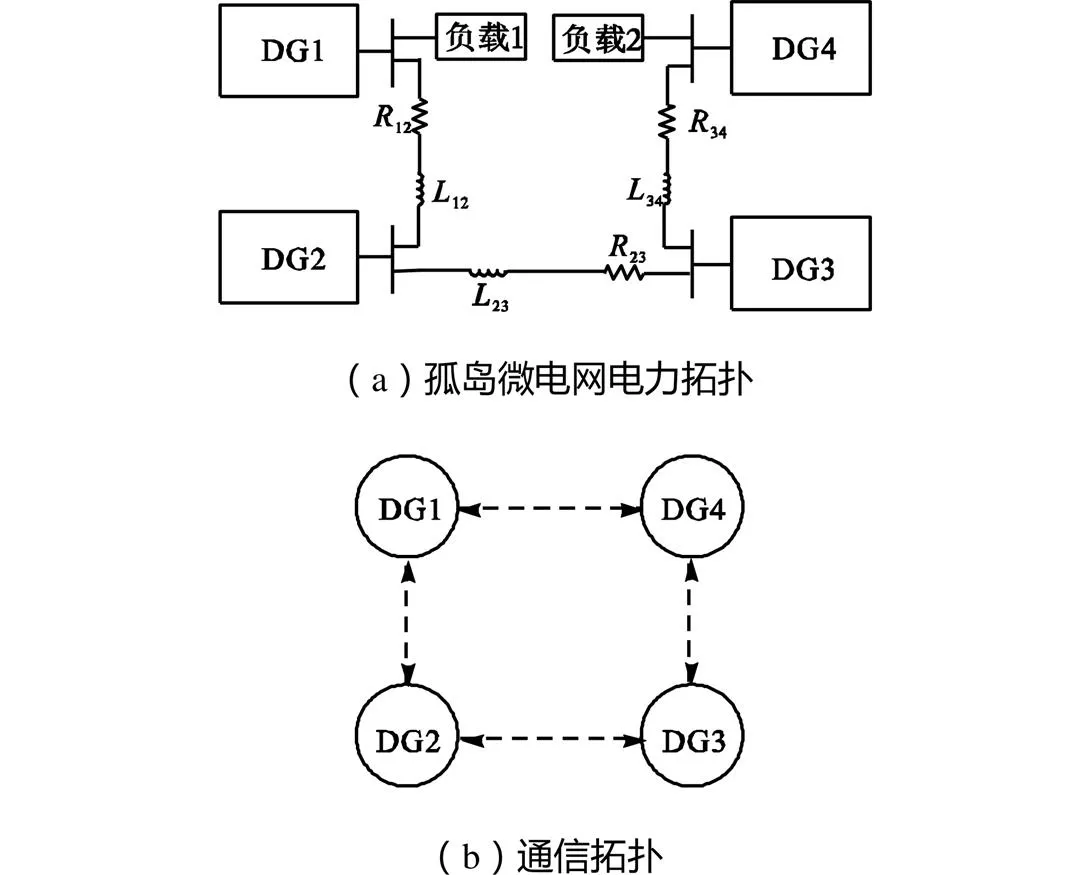
图4 孤岛微电网仿真模型示意

表1 系统参数

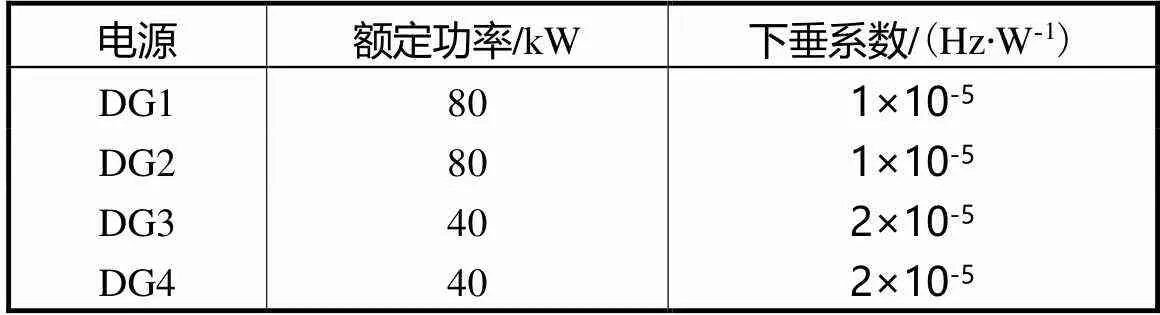
表2 分布式电源参数

表3 DG的控制延时情况

4.1 无控制延时仿真

为了验证本文所提出的频率二次协同控制策略在无控制延时情况下的有效性．在初始时刻，只有负荷1连入微电网中，DG1、DG2、DG3和DG4的输出功率分别为40kW、40kW、20kW和20kW，系统频率为50Hz．在2s时负荷2接入系统，未加入二次协同控制策略和加入二次协同控制策略后的分布式电源输出频率如图5(a)所示，分布式电源输出功率如图5(b)所示．

从图5(a)可以看出，有功负荷增加对频率影响较大，在没有加入二次协同控制时，频率从50.0Hz下降到49.8Hz．在5s时激活二次调频控制策略，频率从49.8Hz恢复到50.0Hz，实现频率的无差控制．由图5(b)可见，在此过程中DG1、DG2、DG3和DG4的输出功率变为了60kW、60kW、30kW和30kW．4个分布式电源按2∶2∶1∶1的比例，在稳态时实现了对新增负荷的合理分配．

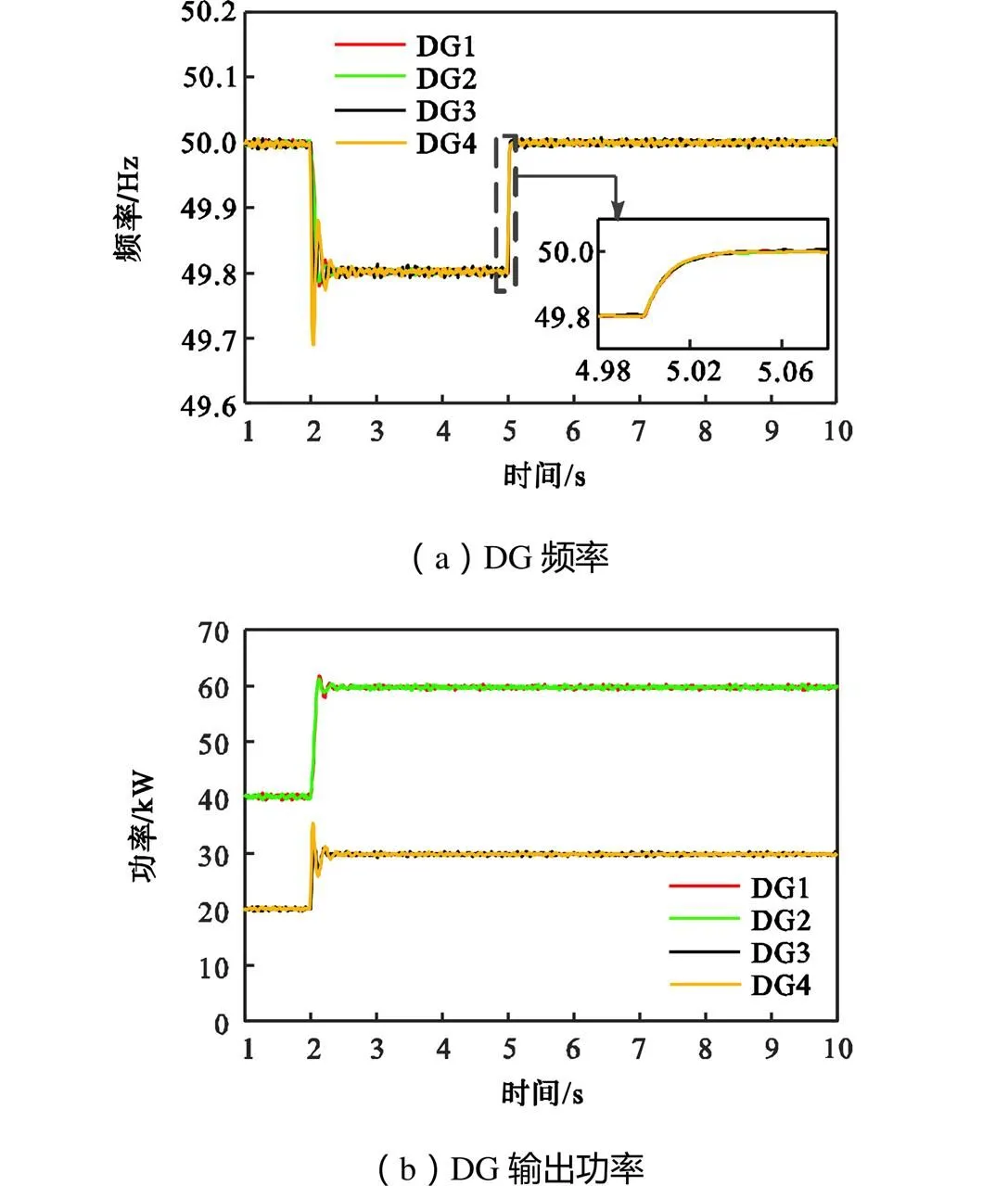
图5 未考虑控制延时情况下的仿真结果

4.2 考虑控制延时仿真

本次仿真验证了本文所提延时临界值计算方法的有效性．系统初始状态与第4.1节中相同．

工况1：控制延时设定为表3中的工况1，在2s时负荷2接入系统，DG输出频率如图6(a)所示．因为负荷变化频率出现偏差，在5s激活二次控制策略时由于控制延时小于本文判据给出的临界值，在二次协同控制作用下，频率最终稳定在额定值．二次调频控制变量如图6(b)所示，由于控制延时小于临界值，DG的二次调频控制变量(表示下垂曲线的平移量)也是收敛的．如图6(c)所示，在此过程中4个分布式电源按2∶2∶1∶1的比例，在稳态时实现了对新增负荷的合理分配．

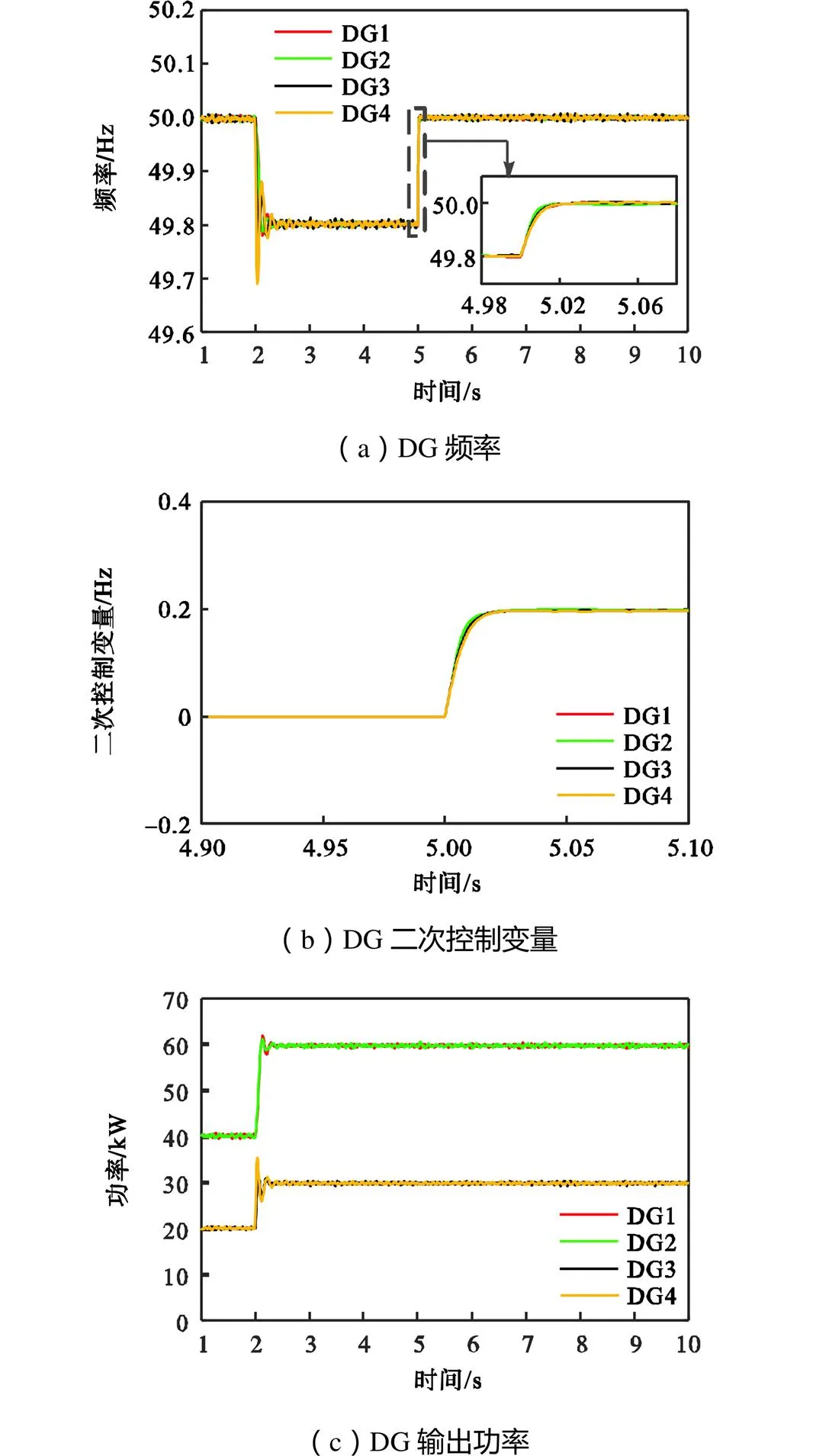
图6 控制延时小于临界值情况下的仿真结果

工况2：控制延时设定为表3中的工况2，在2s时负荷2接入系统．DG输出频率如图7(a)所示．在5s时激活二次控制策略，因为控制延时远大于本文判据给出的临界值，导致协同控制系统不稳定，DG的输出频率出现发散的情况．二次调频控制变量如图7(b)所示，二次调频控制变量(表示下垂曲线的平移量)也是发散的．如图7(c)所示，DG的输出功率也出现发散不稳定的情况．

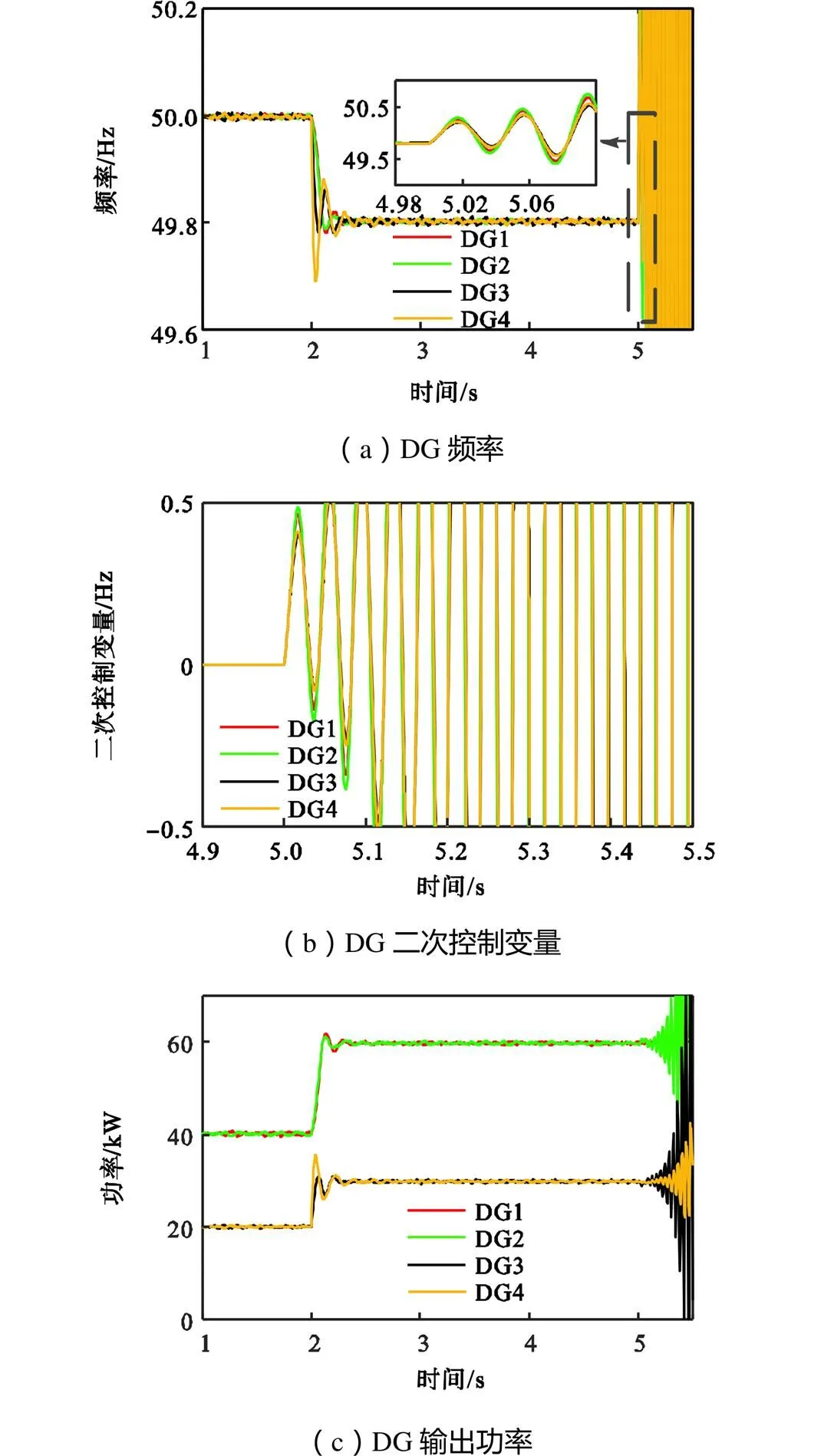
图7 控制延时大于临界值情况下的仿真结果

4.3 改进控制策略仿真

系统初始状态与第4.1节中相同，在2s时将负荷2接入系统，5s时激活二次控制策略，在工况2的情况下，分别使用改进前和改进后的频率二次协同控制策略．在＝0.0003时，在改进后策略控制下DG的输出频率如图8(a)所示，DG的输出功率如图8(c)所示．

由图8可见，在工况2情况下，改进控制策略可使系统稳定运行．

由以上仿真结果可知，频率二次协同控制策略可以实现频率的恢复，但控制延时会对二次协同控制策略造成影响，超出延时临界值时会造成协同控制策略失效，进而导致整个系统失稳．改进的频率二次协同控制策略可以使系统在更大的延时下稳定运行．

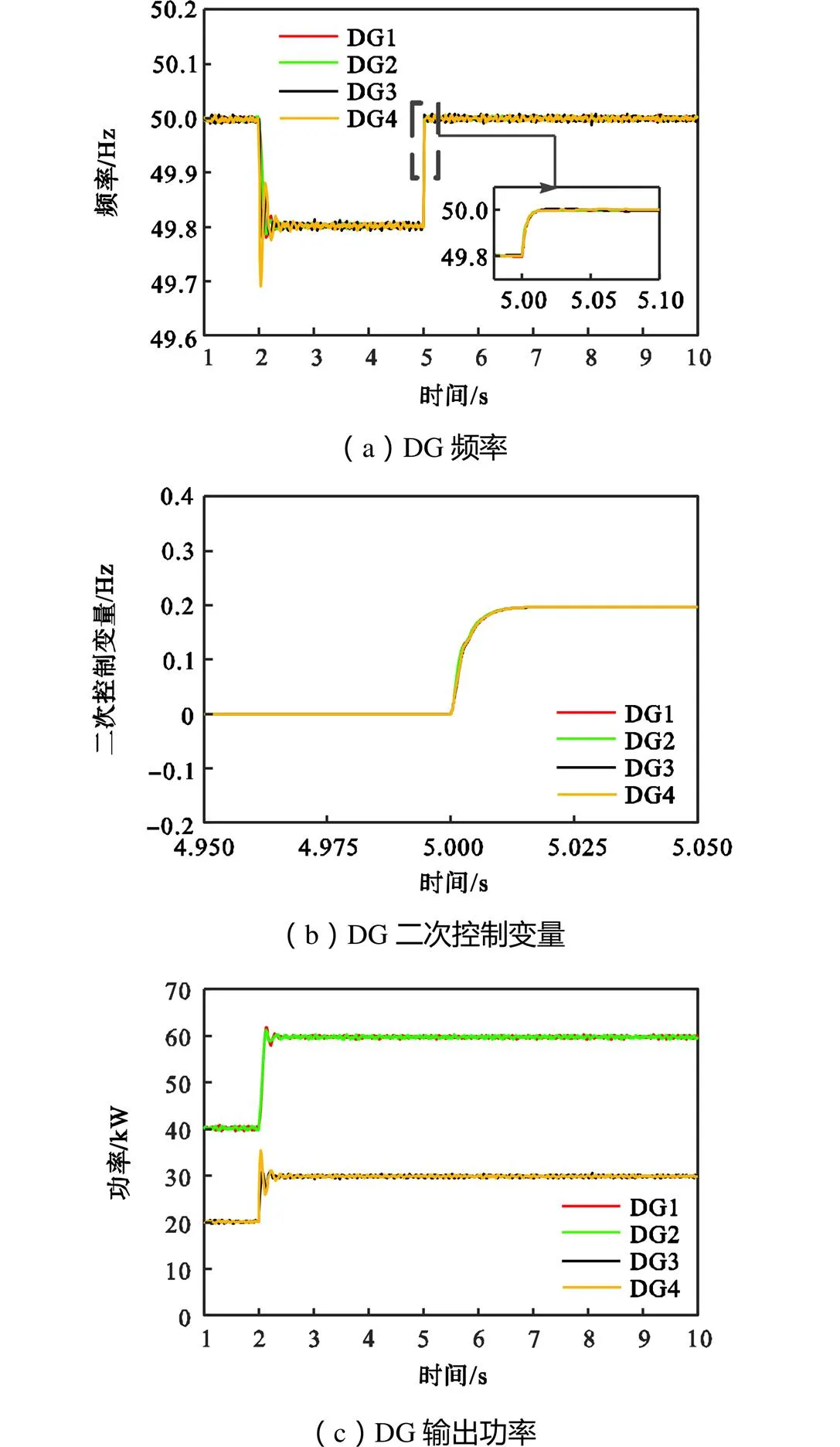
图8 控制延时大于临界值情况下改进型策略仿真结果

5 结 论

本文对孤岛微电网频率二次控制技术开展研究，针对传统集中式频率二次控制可靠性低、可拓展性不足等问题，设计了频率二次协同控制策略，重点分析并讨论了通信延时和控制延时对系协同控制策略稳定性的影响，并给出了改善协同控制系统稳定性的设计方法和改进措施．通过理论分析和多工况仿真实验验证，获得以下结论．

(1) 控制延时会影响分布式协同控制系统的稳定性，其稳定性主要取决于系统参数决定的控制延时临界值．

(2) 通过改进频率二次协同控制策略，可以提升分布式协同控制系统的稳定裕度，使其在更大的控制延时范围内保证微电网稳定运行．

(3) 基于分布式协同控制的频率二次协同控制策略是可行、有效的，在适宜的控制参数下，可以保证孤岛微电网系统的频率品质．

［1］ 刘 青，赵 洋，李 宁，等. 基于分布式神经动力学算法的微电网多目标优化方法[J]. 电力系统保护与控制，2021，49(11)：105-114.

Liu Qing，Zhao Yang，Li Ning，et al. Multiple object-tive optimization of a microgrid based on a distributed neural dynamics algorithm[J]. Power System Protection and Control，2021，49(11)：105-114(in Chinese).

［2］ 余贻鑫. 面向21世纪的智能电网[J]. 天津大学学报(自然科学与工程技术版)，2020，53(6)：551-556.

Yu Yixin. A brief description of the basics of the smart grid[J]. Journal of Tianjin University(Science and Technology)，2020，53(6)：551-556(in Chinese).

［3］ Zhang Y，Shotorbani A M，Wang L，et al. Distributed secondary control of a microgrid with a generalized pi finite-time controller[J]. IEEE Open Access Journal of Power and Energy，2021，8：57-67.

［4］ 梁 英，盛万兴，钟庆昌，等. 基于同步逆变器的微电网二次调频策略及特性分析[J]. 中国电机工程学报，2017，37(2)：391-402.

Liang Ying，Sheng Wanxing，Zhong Qingchang，et al. Secondary frequency regulation strategies and characteristic analysis of synchronverter-based microgrids[J]. Proceedings of the CSEE，2017，37(2)：391-402(in Chinese).

［5］ Alghamdi S，Schiffer J，Fridman E. Synthesizing sparse and delay-robust distributed secondary frequency controllers for microgrids[J]. IEEE Transactions on Control Systems Technology，2021，29(2)：691-703.

［6］ Xu Y，Sun H，Gu W，et al. Optimal distributed control for secondary frequency and voltage regulation in an islanded microgrid[J]. IEEE Transactions on Industrial Informatics，2019，15(1)：225-235.

［7］ Chen M，Xiao X，Guerrero J M. Secondary restoration control of islanded microgrids with a decentralized event-triggered strategy[J]. IEEE Transactions on Industrial Informatics，2018，14(9)：3870-3880.

［8］ Tong Q，Yang L，Wen H，et al. Event-triggered updating method in centralized and distributed secondary controls for islanded microgrid restoration[J]. IEEE Transactions on Smart Grid，2020，11(2)：1387-1395.

［9］ 陈 刚，李志勇，韦梦立. 孤岛微电网的分布式固定时间二次协调控制[J]. 控制与决策，2019，34(1)：205-212.

Chen Gang，Li Zhiyong，Wei Mengli. Distributed fixed-time secondary coordination control of islanded microgrids[J]. Control and Decision，2019，34(1)：205-212(in Chinese).

［10］ Dehkordi N M，Moussavi S Z. Distributed resilient adaptive control of islanded microgrids under sensor/actuator faults[J]. IEEE Transactions on Smart Grid，2020，11(3)：2699-2708.

［11］ Wang Y，Wang X，Chen Z，et al. Small-signal stability analysis of inverter-fed power systems using component connection method[J]. IEEE Transactions on Smart Grid，2018，9(5)：5301-5310.

［12］ 余志文，艾 芊. 基于多智能体一致性的微电网自适应下垂控制策略[J]. 电力自动化设备，2017，37(12)：150-156.

Yu Zhiwen，Ai Qian. Adaptive droop control strategy for microgrid based on consensus of multi-agent system[J]. Electric Power Automation Equipment，2017，37(12)：150-156(in Chinese).

［13］ Shahab M A，Mozafari S B，Soleymani S，et al. Stochastic consensus-based control of μGs with communication delays and noises[J]. IEEE Transactions on Power Systems，2019，34(5)：3573-3581.

［14］ Chen G，Guo Z. Distributed secondary and optimal active power sharing control for islanded microgrids with communication delays[J]. IEEE Transactions on Smart Grid，2019，10(2)：2002-2014.

［15］ Lou G，Gu W，Sheng W，et al. Distributed model predictive secondary voltage control of islanded microgrids with feedback linearization[J]. IEEE Access，2018，6：50169-50178.

［16］ Zhao C，Sun W，Wang J，et al. Distributed cooperative secondary control for islanded microgrid with Markov time-varying delays[J]. IEEE Transactions on Energy Conversion，2019，34(4)：2235-2247.

［17］ Kada B，Khalid M，Shaikh M S. Distributed cooperative control of autonomous multi-agent UAV systems using smooth control[J]. Journal of Systems Engineering and Electronics，2020，31(6)：1297-1307.

［18］ Du Y，Tu H，Yu H，et al. Accurate consensus-based distributed averaging with variable time delay in support of distributed secondary control algorithms[J]. IEEE Transactions on Smart Grid，2020，11(4)：2918-2928.

［19］ 李水天，林 涛，盛逸标，等. 面向次/超同步振荡的控制器参数稳定域构建[J]. 中国电机工程学报，2020，40(22)：7221-7230.

Li Shuitian，Lin Tao，Sheng Yibiao，et al. Construction of stability region of control parameters against sub/super synchronous oscillation[J]. Proceedings of the CSEE，2020，40(22)：7221-7230(in Chinese).

［20］ Tian Y P，Yang H Y. Stability of distributed congestion control with diverse communication delays[C]// World Congress on Intelligent Control & Automation. Hangzhou，China，2004：1438-1442.

［21］ Singh K，Amir M，Ahmad F，et al. An integral tilt derivative control strategy for frequency control in multimicrogrid system[J]. IEEE Systems Journal，2021，15(1)：1477-1488.

［22］ Verma B，Padhy P K. Robust fine tuning of optimal PID controller with guaranteed robustness[J]. IEEE Transactions on Industrial Electronics，2020，67(6)：4911-4920.

［23］ 刘 美，禹柳飞，宁 鹏. 仪表及自动控制[M]. 北京：中国石化出版社，2015.

Liu Mei，Yu Liufei，Ning Peng. Instrumentation and Automatic Control[M]. Beijing：China Petrochemical Press，2015(in Chinese).

［24］ Pan Y，Li X，Yu H. Efficient PID tracking control of robotic manipulators driven by compliant actuators[J]. IEEE Transactions on Control Systems Technology，2019，27(2)：915-922.

［25］ Gude S，Chu C. Dynamic performance enhancement of single-phase and two-phase enhanced phase-locked loops by using in-loop multiple delayed signal cancellation filters[J]. IEEE Transactions on Industry Applications，2020，56(1)：740-751.

［26］ Ma D，Chen J. Delay margin of low-order systems achievable by PID controllers[J]. IEEE Transactions on Automatic Control，2019，64(5)：1958-1973.

［27］ 周念成，孟潇潇，王强钢. 考虑逆变型分布式电源时滞的孤岛微网小信号稳定分析[J]. 电力系统自动化，2017，41(12)：20-25.

Zhou Niancheng，Meng Xiaoxiao，Wang Qianggang. Small signal stability analysis of islanded microgrid considering time-delay effect of inverter interfaced distributed generator[J]. Automation of Electric Power Systems，2017，41(12)：20-25(in Chinese).

［28］ 刘一鸣，李彦哲，董海鹰，等. 计及时滞环节的孤岛微电网控制器参数优化研究[J]. 电力系统保护与控制，2019，47(12)：22-30.

Liu Yiming，Li Yanzhe，Dong Haiying，et al. Study on parameter optimization of islanded microgrid with time delay[J]. Power System Protection and Control，2019，47(12)：22-30(in Chinese).

Stability Analysis and Improvement of Frequency Cooperative Control Strategy for Island Microgrid Considering Time Delay

Li Zhijun1, 2，Zhang Moufa3，Zhang Jia’an1, 2

(1. State Key Laboratory of Reliability and Intelligence of Electrical Equipment，Hebei University of Technology，Tianjin 300130，China；2. Laboratory of Electromagnetic Field and Electrical Apparatus Reliability of Hebei Province，Hebei University of Technology，Tianjin 300130，China；3. School of Artificial Intelligence，Hebei University of Technology，Tianjin 300130，China)

Primary droop control is widely used in island microgrids. This strategy will cause a steady-state frequency variation between the rated value and actual value when the load changes. Meanwhile，the traditional centralized sec-ondary control of island microgrids has low reliability，insufficient scalability，and other problems. Based on the distributed cooperative control，a frequency secondary cooperative control strategy is designed in this study to over-come the shortcomings of traditional centralized secondary control and eliminate the steady-state frequency variation. Various kinds of delay caused by the acquisition time delay of digital circuits and the limitations of communication conditions among the distributed generations are considered to analyze system stability. The Gerschgorin disk theorem and Nyquist stability criterion were used to analyze the influence of delay on the stability of the frequency secondary cooperative control strategy. A method to judge the stability with delay was proposed by calculating the critical value of control delay. To reduce the influence of delay on the stability of the control strategy，the frequency secondary cooperative control strategy was improved，where the corresponding stability analysis and parameter design method were given. The improved strategy can ensure the operation stability of the system with a larger control delay. Finally，a simulation model of the studied microgrid was established in Matlab/Simulink，and the simulation results demonstrated that the designed frequency secondary cooperative control strategy can realize the frequency recovery in an island microgrid. The control delay can affect the stability of the coordinated control system when it exceeds the critical value. By applying the improved frequency secondary coordinated control strategy，the stability margin of distributed cooperative control system is increased and the stable operation of the microgrid with a larger control delay can be ensured.

islanded microgrid；secondary frequency control；cooperative control；control delay

TM71

A

0493-2137(2022)10-1061-10

10.11784/tdxbz202108038

2021-08-16；

2021-11-10.

李志军（1964— ），男，博士，教授.

李志军，zhijun_li@263.net.

河北省科技支撑计划资助项目(15212105).

Hebei Province Technology Support Program(No. 15212105).

(责任编辑：孙立华)