基于科氏流量计和PSO-SVM的气液两相流测量研究

孙立军，刘 悦，童杰林，陈水源，高静宇

基于科氏流量计和PSO-SVM的气液两相流测量研究

孙立军1, 2，刘 悦1, 2，童杰林3，陈水源1，高静宇1, 2

(1. 天津大学电气自动化与信息工程学院，天津 300072；2. 天津市过程检测与控制重点实验室，天津 300072；3. 沃森测控技术有限公司，廊坊 065009)

科氏流量计；气液两相流；支持向量机；粒子群优化算法；含气率

科氏流量计是一种可直接测量流体质量流量的高精度流量计，也可测量密度、体积流量和温度，广泛应用于单相流测量，目前质量流量测量精度为0.1%．但是，在气液两相流情况下，科氏流量计的质量流量测量误差急剧增加．由于气液两相流本身的流动复杂性，流动形态随含气率、温度、压力等因素的变化而变化，质量流量测量误差的修正有很大难度．在两相流工况下，除测量液相质量流量以外，通常还需要测量体积含气率(GVF)．

科氏流量计在测量两相流时，首先要解决的是由于测量管阻尼增加且变化快，导致科氏流量计停振．这就需要快速跟踪相位、幅度、频率信息、稳定的控制回路和快速信号处理技术，维持测量管正常振动，进而减小测量误差．

李苗等[1]提出一种随机序列、正反馈驱动以及信号合成的驱动优化方法，以维持测量管稳定振动. Zamora等[2]设计了奔腾处理器和FPGA结合控制的数字式科氏转换器．利用数字信号处理方式处理底层传感器信号，并基于波形合成的数字式驱动方法驱动测量管振动，可实现两相流测量．Li等[3-4]针对传感器和驱动器信号之间会出现时间延迟问题，提出了复杂带通滤波器(CBF)、复杂陷波滤波器(CNF)和两者结合的CBF-CNF复杂滤波器，3种复杂信号处理方法，并进行了两相流实验．结果表明，复杂的带通算法与控制算法相结合，在50%的实验中使质量流量测量的标准偏差降低了3倍或更多．

针对科氏流量计转换器改进，提高处理速度的快速性，对减小测量误差的效果有限．为了更有效地解决质量流量测量误差问题，科研工作者构建了许多两相流误差修正模型．模型的建模方式主要有机理建模和数据驱动建模．

Hemp等[5]提出的气泡模型和压缩效应模型，是比较经典的质量流量误差修正模型，分别解释了质量流量产生负误差和正误差的原因．气泡模型分析气泡在测量管中的受力情况，气泡的振幅远大于液体的振幅，气泡和液体发生解耦效应，科氏流量计检测到的惯性减少，质量流量低于真实值．压缩效应的分析方法是将气液看成一个整体，构建二阶质量弹簧模型，在两相流情况下，测量值大于真实值．Liu等[6]在气泡模型和压缩效应的基础上，增加了阻尼影响公式，利用半经验方法，将整个模型的适用范围提高到含气率40%以内，质量流量修正后相对误差范围小于10%，含气率的预测绝对误差小于5%．中国石油大学的赵玉琦[7]和李珊珊[8]分别针对环状流、分层流的流动理论，以直管科氏流量计梁模型为基础，建立了适用于环状流、分层流测量的两相流理论，实验和模型结果吻合，但是针对分层流的模型计算量太大，对两相流的测量反应较慢．这些物理模型的构建基于大量假设，并且没有考虑管道的几何形状、气泡分布、流型等重要因素，模型的适用范围有限，理论分析与实验结果存在很大差异．

基于实验数据驱动的模型可直接建立参数和输出变量的关系，在含气率较大的范围内，质量流量误差修正效果远优于机理模型．科氏流量计测量两相流的误差可重复，是应用数据驱动方法的前提．常见的应用机器学习方法包括神经网络和支持向量机(SVM). Liu等[9]使用神经网络，建立了输入参数为温度、阻尼、密度降、流量测量值，输出变量为液体质量流量误差的预测模型，密度降至小于35%时，质量流量的误差基本能减少到±2%．马龙博等[10]借助支持向量机算法，在油水两相流工况下，为双U型科氏流量计对油水两相的质量流量进行了预测，总体质量流量的相对误差在1%以内，分相质量流量误差在 ±8%以内．侯其立[11]采用前馈神经网络对气液两相流条件下的测量误差进行校正，输入变量为液相质量流量测量值和实测密度降．实验结果表明，当水流量为3～15kg/min，气体体积分数小于25%时，流量误差在±3.5%以内，密度误差在±1.5%以内．除科氏流量计以外，Wang[12]添加了与相成分相关的差压、电导传感器，通过3种输入变量选择方法，确定了与液体质量流量修正最相关的变量，包括密度测量值、质量流量测量值、差压和阻尼，对于气体体积分数预测最相关的变量，是密度测量值、质量流量测量值和阻尼．评估了支持向量机、遗传算法、神经网络模型的准确性和鲁棒性，SVM的性能最好．乐静[13]基于网格搜索参数寻优的方法，对液相量程比约为3∶1，密度降为0～35%工况下，科氏流量计测量质量流量误差进行修正，修正后误差在－2.5%～3%．Meribout等[14]设计了基于多级人工神经网络的测量算法，结合理想气体状态方程和气泡理论模型估算溶解在液相中的气体数量．在整个GVF范围，质量流量和密度的相对误差绝对值不超过2.5%．但在实验管路上需要安装气液分离器，以提供构建模型的分相变量．

在数据驱动建模的研究中，构建的模型大多只对质量流量进行修正，并且量程范围较小，或利用密度测量值计算的密度降反映含气率，本身测量误差很大，且不能量化气体体积分数；Wang[12]将差压作为输入变量建立基于SVM的质量流量修正模型，模型的预测效果很好，但基于网格搜索参数寻优方法，需要花费大量的时间，同时需外接差压变送器，在实际应用中具有局限性．

为解决上述问题，本文进行标准表实验，获取建模数据，结合粒子群参数寻优算法，改进SVM算法，建立了含气率为0～30%，液体质量流量范围为200～880kg/h的两相流质量流量修正和含气率预测模型．同时使用新变量代替差压变量或更改模型结构的方法，构造了一体化测量模型，不需要外接差压变送器，简化两相流测量，并且保证了质量流量修正和含气率预测模型的准确性．

1 支持向量机

支持向量机由Vapnik于1995年开发，用于解决基于统计学习理论和结构风险最小化的分类问题[15].此后，该方法已扩展到回归和预测问题领域[16]．两相流工况下液体质量流量和气体体积分数的预测属于典型回归问题．

1.1 回归模型(SVR)的原理

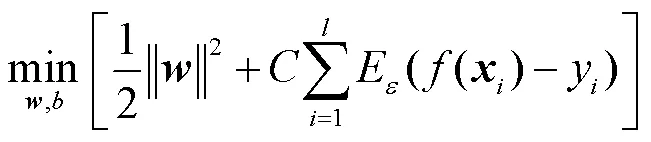
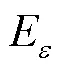
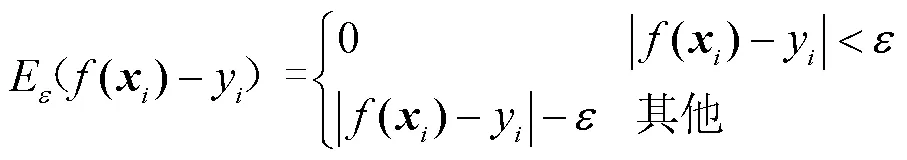
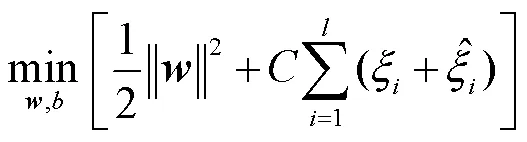
引用拉格朗日乘子，将带约束的目标优化函数转化为无约束的拉格朗日函数，线性模型转换为对偶问题，得到优化问题的解和．

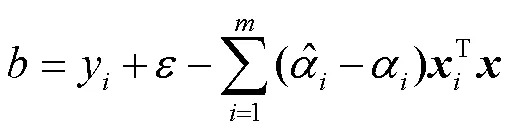
将式(4)代入到线性模型中得

式中为支持向量的个数．

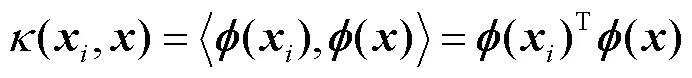
最终的支持向量机输出模型为

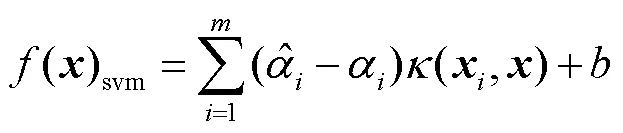
1.2 模型参数

为得到预测性能最优的SVM回归模型，需要优化目标函数的惩罚因子和核函数的参数．

优化目标函数中的取值范围有限，应满足模型复杂度较低的情况下，不满足约束的样本尽可能少，当取有限值时，允许一些样本不满足约束；当取无穷大时，迫使所有样本均满足约束，容易出现过拟合现象．

支持向量机模型中常见的核函数包括多项式核函数、高斯核函数、RBF 核函数等，本文采用目前应用最广泛的 RBF 径向基函数．

1.3 基于粒子群优化算法参数寻优

常见的寻优方式为网格搜索算法，设定区间足够大，且步长足够小时，会找出局部最优解，但相当浪费时间[19-20]；而粒子群算法寻优速度快、效率高．

粒子群优化算法对支持向量机参数和参数进行全局寻优，将和两个参数看作两个粒子群，首先设置种群规模、迭代参数等参数，进行种群和速度初始化，将随机产生的和输入到SVM模型进行训练，模型交叉验证的均方误差(CVmse)作为模型适应度函数，粒子的适应度最小代表此时粒子位置最优，当迭代次数满足设定值，则优化算法结束．将最优的参数、代入SVM模型进行训练，后通过测 试集进行模型性能测试，整个建模的步骤如图1 所示[21-22]．

图1 PSO-SVM模型示意

2 实验数据的获取

2.1 实验装置

实验装置由水路和气路两路通道组成．实验原理如图2所示，水从水槽中抽出，打入水塔，通过水流量装置依次流入液相标准表(涡轮流量计)、被检表(科氏流量计)、换向器直接流入水槽．水流量通过气动开关阀、电动调节阀、手阀进行调节．气路通过SV1开启，由气泵产生的气体，经过储气罐、调压阀、缓冲罐、稳压阀、针型阀，调节和稳定气流量后，经气相标准表与水混合，形成气液两相流后经科氏流量计流回水槽，空气从水中溢出．

科氏流量计测量两相流的前提是能准确测量单相流．实验选用Walsn VS 系列的DN10 V型双弯管科氏流量计，结合实验室开发的基于ZYNQ的科氏流量计转换器，液相质量流量的计量精度为0.1%，重复性优于0.02%．科氏流量计还可提供密度信息，单相流工况下，密度测量的相对误差为1%，但在两相流工况下，密度测量误差增加．涡轮流量计作为标准表的测量精度为0.3%，符合两相流实验液相测量要求．气相标准表选用Alicat气体质量流量计(0～600mL/min)和浮子流量计(0.04～0.40m3/h)两个仪表，以实现实验含气率范围内的气相流量测量，仪表精度分别为1.0%和2.5%．

科氏流量计两端的差压表(0～100kPa)和下游压力表(0～400kPa)的精度均为0.1%，采用响应时间小于2ms的快速响应仪表，可记录两相流动态信息.

2.2 实验目的与方法

实验目的是在含气率0～30%、液体质量流量量程为0～1000kg/h的条件下，制造不同的气液两相流工况，采用科氏流量计和差压变送器配合测量的测量方式，收集充足的输入输出实验数据集，以便分析两相流规律和构建数据驱动的预测模型．

实验采用控制水流量不变，改变气流量的方法，制造不同实验工况．每个水流量点在0～30%内，至少取15个等间隔含气率点．由于含气率低，气体的质量可忽略不计，通过比较液相标准表和科氏流量计测量值计算质量流量误差．两相流的质量流量测量精度与标准表涡轮流量计精度相同，为0.3%．为保证实验的可靠性，每组实验持续时间为30s，重复3～4次．其中，含气率为工况含气率，利用理想气体状态方程折算到工况压力下的含气率．

图2 两相流实验装置原理

为了训练模型，收集了85组记录(图3中的圆形标记)的数据集；另外22组记录(图3中的三角形标记)的数据集用于测试模型的性能．测试集不参与训练，在不同流量下获得的测试数据集，有助于评估数据驱动模型的泛化能力．

图3 实验点汇总

2.3 实验数据变量

实验中可获得的数据变量、模型的可输入变量、输出变量汇总，如表1所示．

表1 数据变量

2.4 实验结果与分析

2.4.1 原始误差分析

根据气液两相流装置的实验原理，科氏流量计测量质量流量原始误差计算公式为

图4 质量流量原始误差

Fig.4 Original errors of the mass flow

当液相质量流量在200～880kg/h变化，含气率在0～30%变化时，测量误差表现为非线性，气液两相流测量误差最大为-23%．其次，在不同的液体流量下，质量流量误差随含气率变化趋势不同．总体呈下降趋势，均为负值．这一现象符合解耦误差模型，气体的加入导致一部分液体不随测量管振动，科氏流量计测量液体的质量流量减小，产生负误差，气体含量越多此现象越明显．同时，3次实验的误差波动范围随液相流量和含气率增加而增加．这是由于液相流量越大，同一含气率气相流量越大，两者混合达到稳定所需时间越长，自身波动剧烈，实验重复性较低.

2.4.2 实验现象分析

依据实验数据计算，驱动增益与含气率的关系如图5(a)所示．在液相质量流量不变的情况下，随着含气率上升，测量管阻尼增加，驱动增益随气相流量增加而增加．这是由于设计驱动电压有上限值，如图5(b)所示，达到一定电压之后，驱动最大能量保持不变，然而阻尼依旧增加，科氏流量计的振动将越来越困难，检测器检测到的科氏流量计测量管振动幅值将越来越小，如图5(c)所示．

如图6所示，同一水流量，随含气率增加，两相流压降增加趋势接近线性；同一含气率，随液相流量增加，两相流压降增加．为了更加直观地呈现含气率与两相流压降关系，借鉴孔板流量计的流出系数公式，消除实验压力变化造成气体密度变化的影响，即

图5 测量管驱动和振动参数与含气率关系

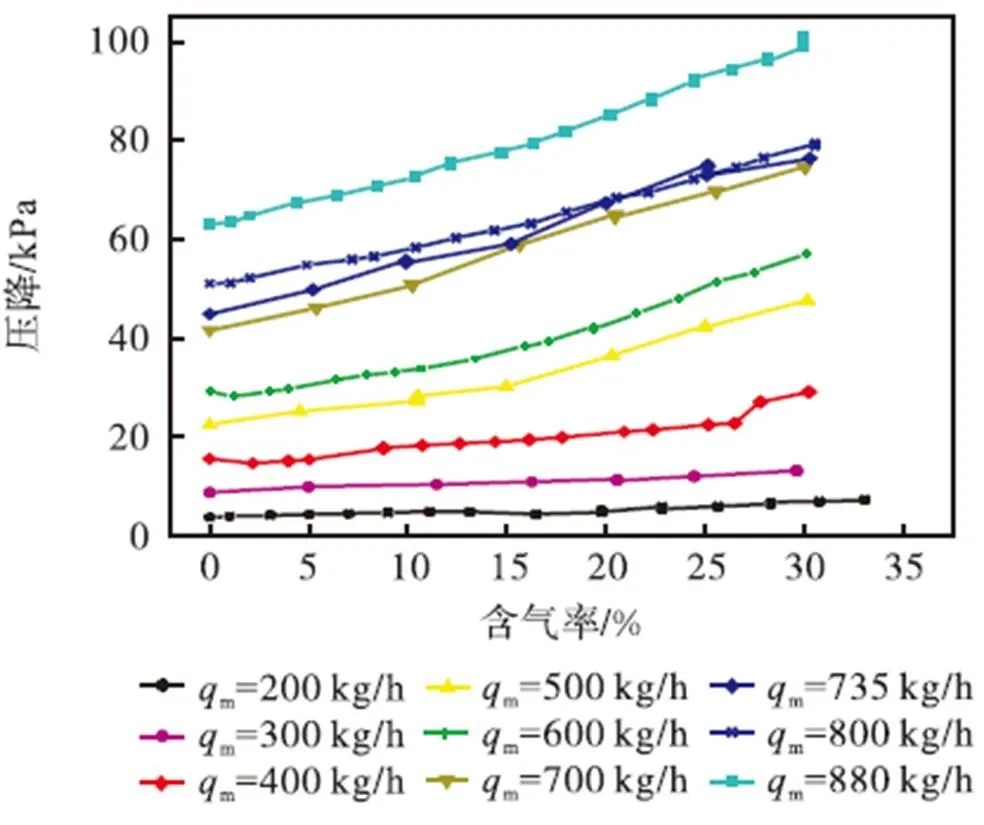
图6 含气率与压降关系

含气率与流出系数关系如图7所示，接近线性关系，拟合精度很高，2＝0.9448．若使用流出系数与含气率的关系估计含气率的值，含气率预测的绝对误差在6%之内．

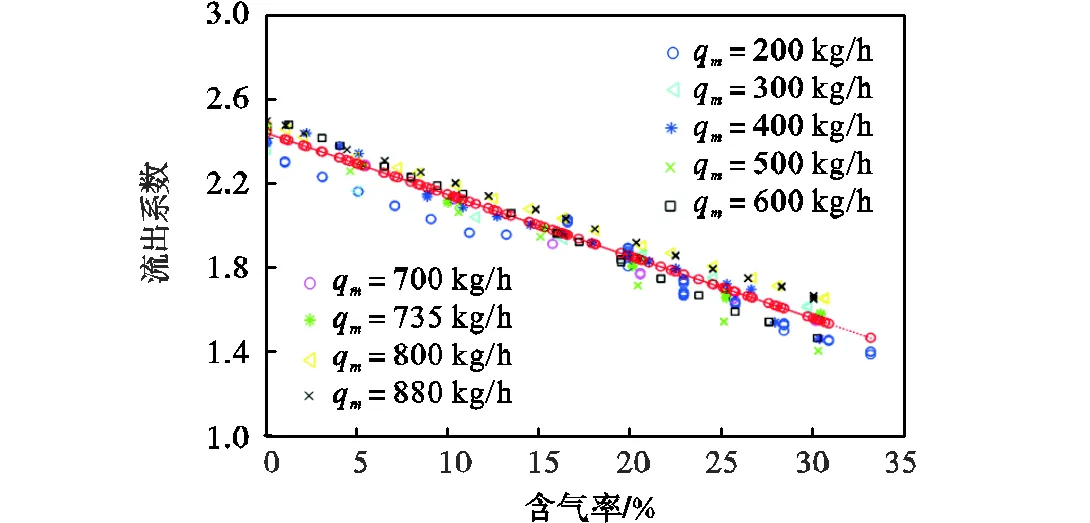
图7 含气率与流出系数关系()

2.4.3 动态信号

差压信号可提供相含率信息，质量流量测量值直接反映两相流对科氏流量计测量的影响．由图4可知，质量流量误差在200kg/h和800kg/h流量点下有明显差异．因此，主要对200kg/h和800kg/h的差压和质量流量测量值进行记录与分析．

如图8所示，两个流量点在不同GVF工况下，差压原始信号的波动情况．由图8可知，差压随含气率增加，波动更加剧烈．200kg/h流量点的不同曲线之间出现重叠；800kg/h流量点不同曲线差压均值差异明显．为去除流量点大小对差压波动的影响，计算了反映差压相对波动的相对标准偏差(RSD)，计算公式为

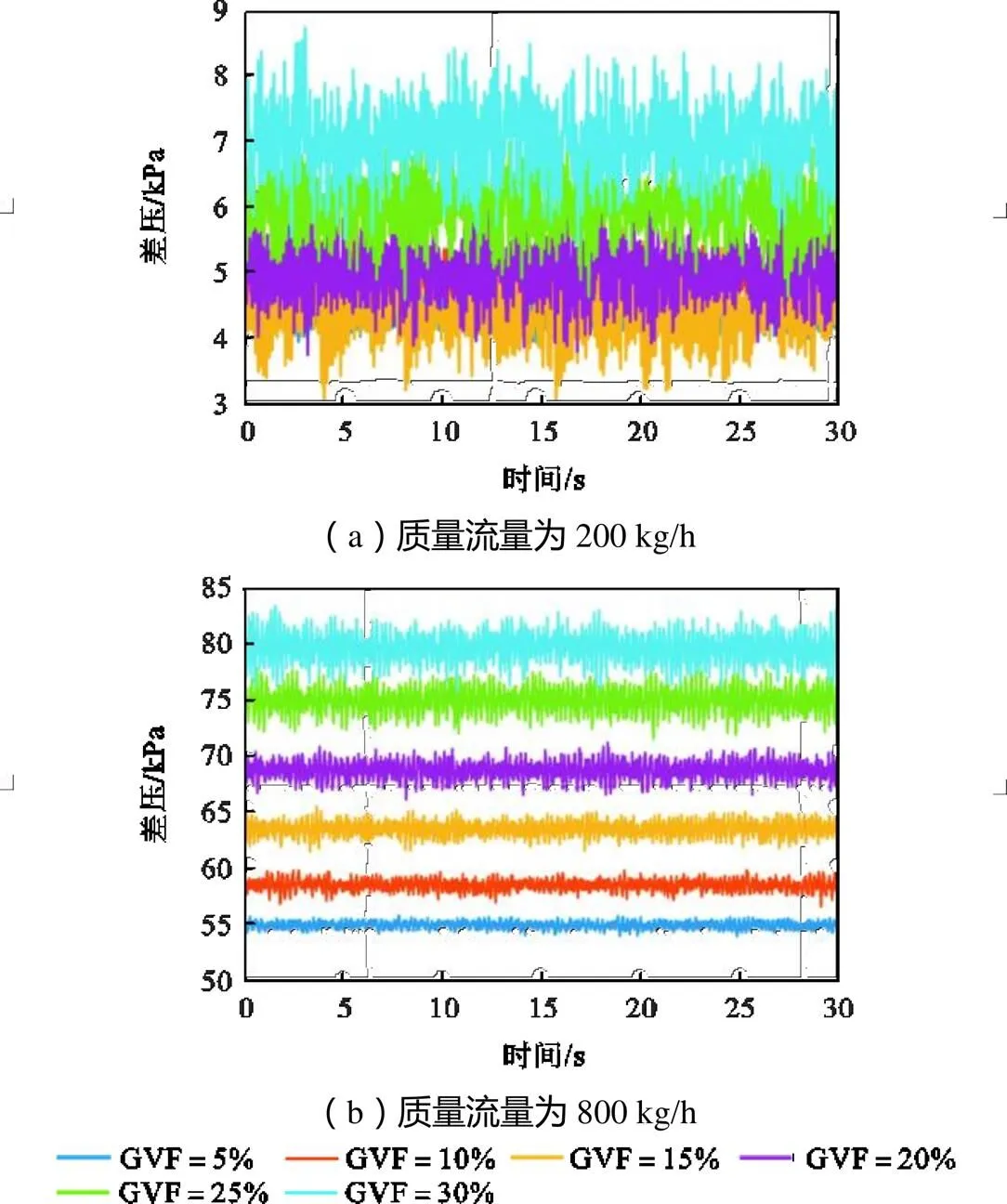
图8 30s内差压波动信号

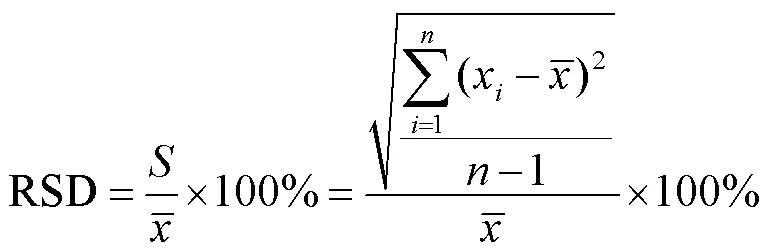
如图9所示，200kg/h流量点的差压相对波动明显高于800kg/h流量点的差压相对波动．由图9可知，差压相对标准偏差随含气率变化规律与质量流量误差绝对值的变化趋势相似．

图9 相对波动随含气率变化趋势

Fig.9 Trend of relative fluctuation of differential pres-sure with GVF

如图10所示，两个流量点在不同GVF工况下，质量流量测量值信号在30s内的波动情况．质量流量随含气率增加，波动更加剧烈．200kg/h流量点随含气率增加，质量流量测量值均值有明显的下降，因此，质量流量测量误差为负误差．800kg/h流量点的均值无明显变化，质量流量相对波动如图11所示，200kg/h流量点的质量流量相对波动量值远小于800kg/h流量点，随着含气率增加，800kg/h流量点质量流量的相对波动增加量远大于200kg/h流量点．在同一含气率下，随着流量增加，质量流量的相对波动增加．因此，质量流量的相对波动对不同含气率、不同流量具有分辨能力，可作为模型的可选输入变量．

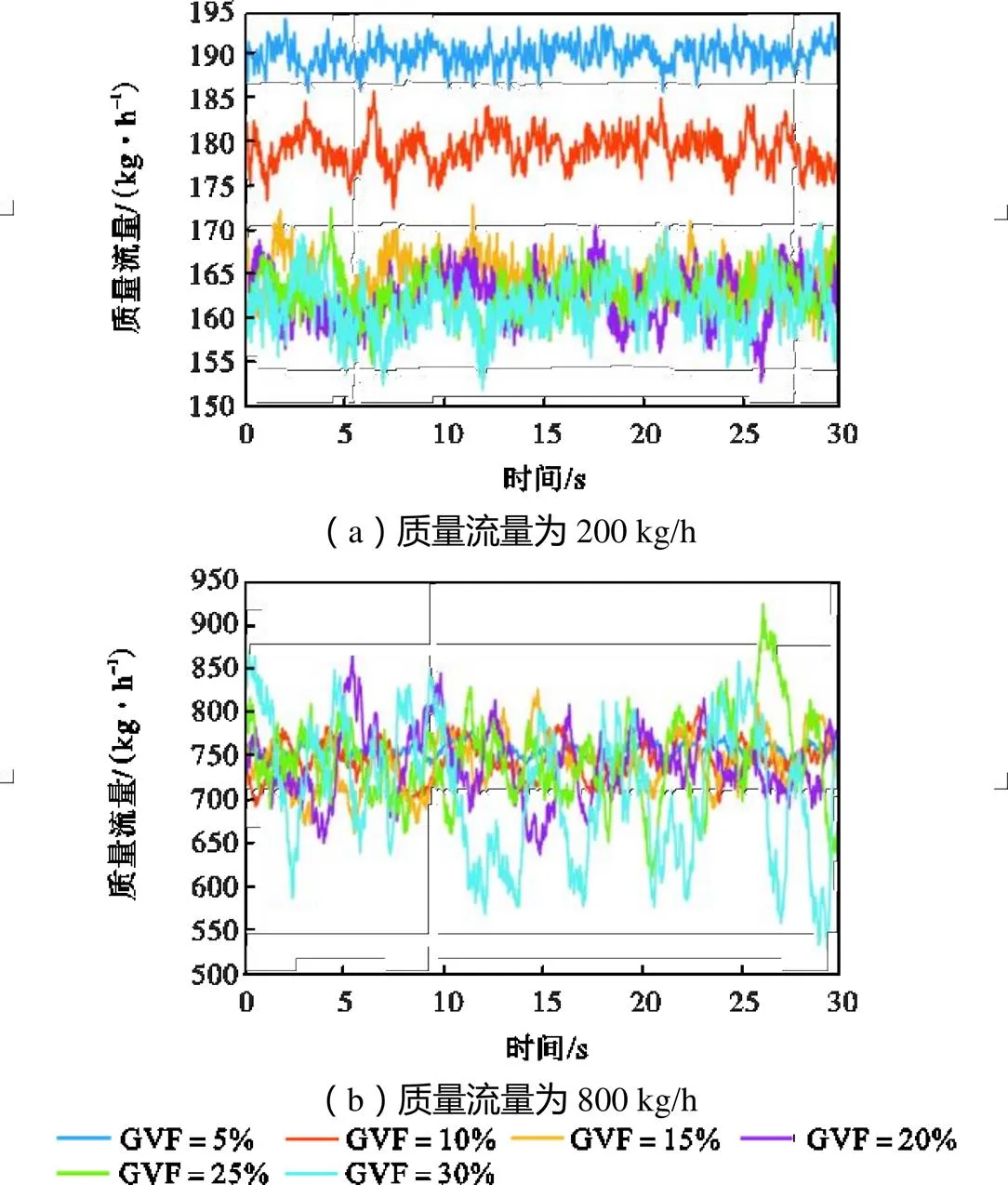
图10 30s内质量流量波动信号

3 模型与预测效果

3.1 变量选择

质量流量测量值、密度测量值、阻尼、差压作为输入变量，训练SVM模型，对质量流量修正达到了很好的效果．质量流量测量值、密度测量值、阻尼作为输入变量，训练SVM模型，对含气率预测的误差最小[23]．因为驱动增益的趋势与阻尼的变化趋势一致[9]，阻尼的检测还需搭建电路[24]，本文使用驱动增益替代阻尼．与参考文献[24]的训练结果不同，本文用质量流量测量值、密度测量值、阻尼、差压输入变量组合预测含气率，构建的模型预测误差最小．由此可见，差压对本文的质量流量修正和含气率预测都起到了重要作用．

本文构建的测量模型使用的输入变量组合如表2所示，变量符号见表1．表中不包含差压变量，为完全基于科氏流量计自身信号的测量模型．

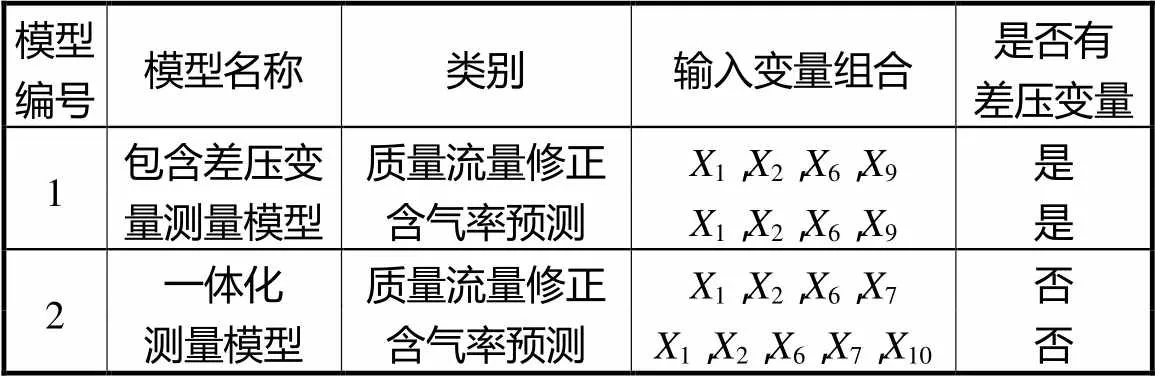
表2 输入变量组合

3.2 包含差压变量的模型预测效果

3.2.1 质量流量修正

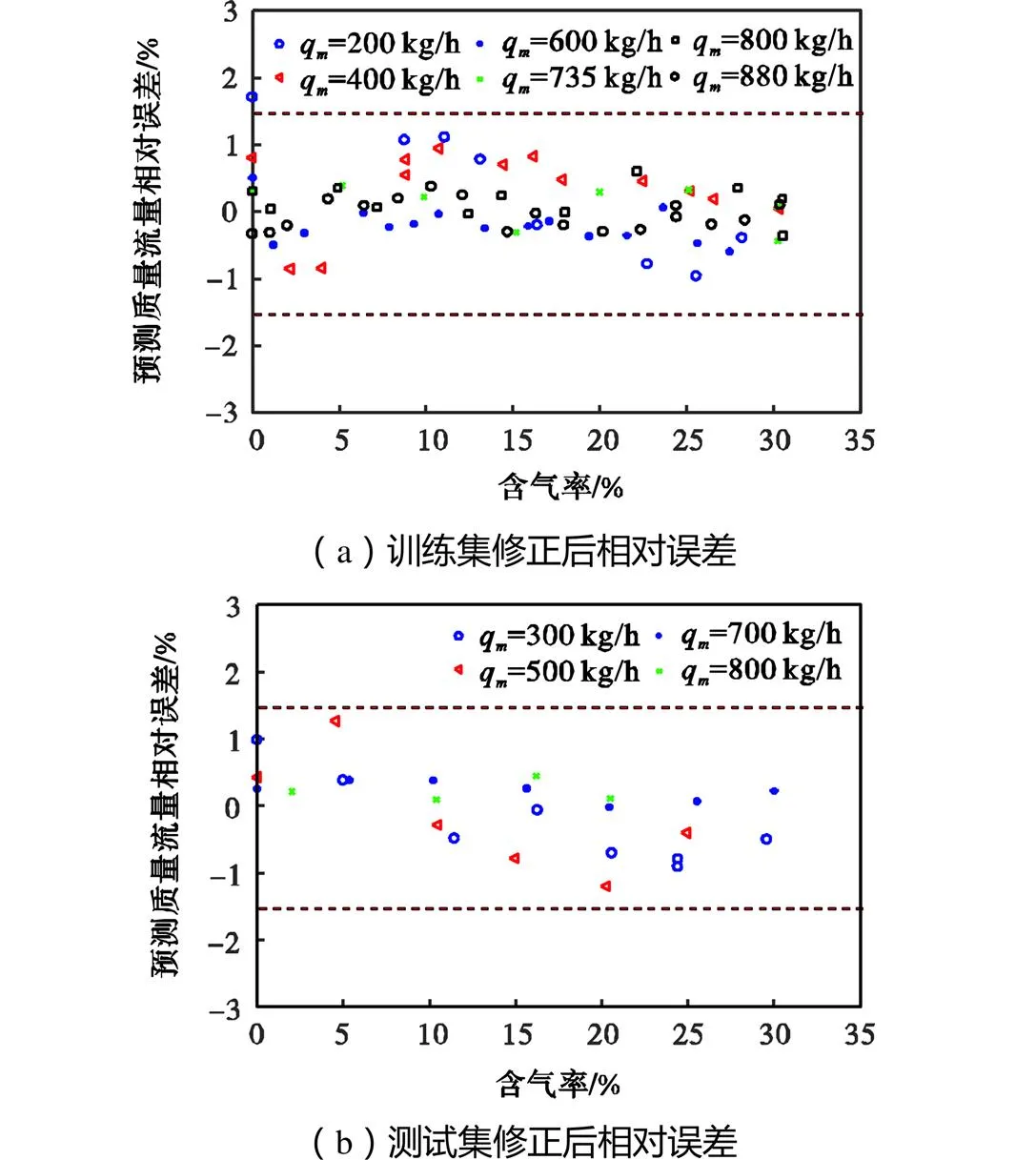
图12 质量流量修正后的相对误差(模型1)

3.2.2 含气率预测

图13 含气率预测绝对误差(模型1)

3.3 一体化测量模型的预测效果

3.3.1 质量流量修正

由第2.4.3节的实验分析可得，质量流量测量值的相对波动对含气率、流量都有分辨能力，因此，将反映质量流量波动情况的质量流量方差替代差压变量作为模型的输入．

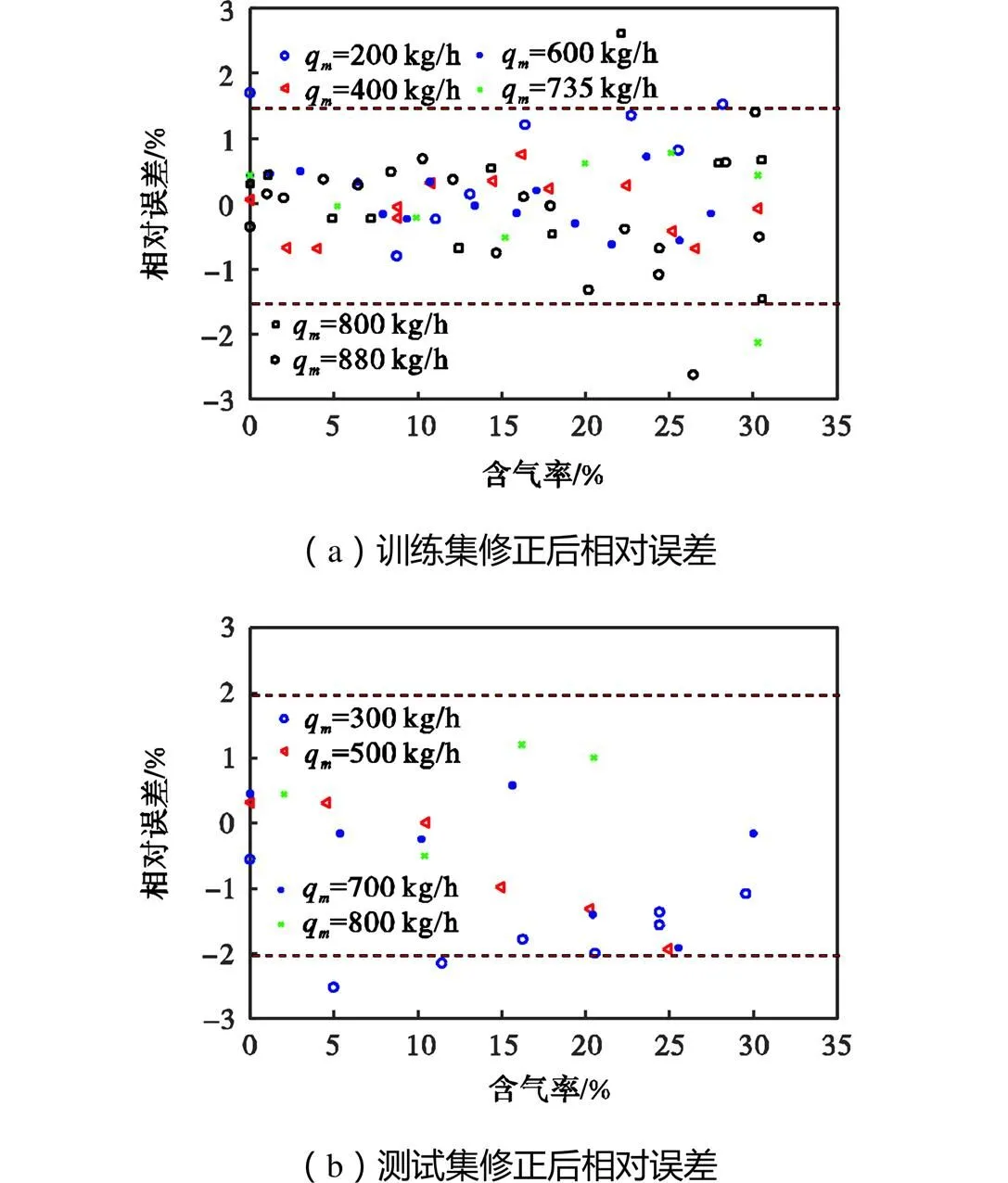
图14 质量流量修正后的相对误差(模型2)

3.3.2 两级SVM结构预测含气率

由第2.4.3节实验分析可得，质量流量误差与差压的相对波动的趋势相似，因此，建立两级SVM模型结构，将质量流量修正结果与科氏流量计质量流量测量值之差，即质量流量修正的绝对偏差作为输入，替代差压变量，含气率预测模型的结构如图15所示.

综上，包含差压变量作为输入变量的质量流量修正和含气率预测，都达到了很好的效果；由于差压变送器需要安装到科氏流量计两端，为简化工艺成本并节省时间，用新变量代替差压变量，对质量流量修正和含气率预测效果与包含差压变量组合的效果接近.

图15 含气率预测模型结构

图16 含气率预测绝对误差(模型2)

3.4 寻优方式优化性能对比

评价寻优方式的性能使用期望输出的均方根误差(MSE)，而测试集的MSE反映了模型的泛化能力、准确性，MSE的计算方法为

由表3可知，与网格搜索寻优算法相比，PSO寻优方式，可以更快地在大范围内找到合适的参数，对于科氏流量计两相流质量流量修正、含气率预测、模型的泛化能力、准确性上都有所提升，运算时间也大幅度缩短．

4 结 语

为构建基于数据驱动的科氏流量计测量质量流量修正模型和含气率预测模型，针对V型双弯管科氏流量计进行了含气率0～30%的气液两相流实验，采用标准表法实验，获得科氏流量计测量两相流的原始数据，宏观分析实验现象，得出含气率和流出系数接近线性关系．对两相流工况下的200kg/h、800kg/h流量点的差压波动信号和质量流量测量值波动信号进行了简单分析．发现差压的相对波动与质量流量测量误差绝对值随含气率变化的曲线类似．

为了得到最优参数，构建质量流量修正和含气率预测的最优模型，用粒子群算法优化支持向量机，构建的模型相比于未经优化的支持向量机模型，寻优时间更短、准确性更高．

未来的工作主要包括两方面，一方面，可将构建的两相流模型写入科氏流量计的转换器，实现在线预测含气率、质量流量．另一方面，本文实验过程中采用了快速响应的差压仪表，能够反映两相流的相含率、流型信息，可进一步对差压信号进行动态信号 分析，提取有用信息以判断科氏流量计中的两相流 状态．

［1］ 李 苗，徐科军，侯其立，等. 数字科氏质量流量计正负阶跃交替激励启振方法[J]. 仪器仪表学报，2010，31(1)：172-177.

Li Miao，Xu Kejun，Hou Qili，et al. Startup method of digital Coriolis mass flowmeter using alternating exciting of positive-negative step signal[J]. Chinese Journal of Scientific Instrument，2010，31(1)：172-177(in Chinese).

［2］ Zamora M，Henry M P. An FPGA implementation of a digital Coriolis mass flow metering drive system[J]. IEEE Transactions on Industrial Electronics，2008，55(7)：2820-2831.

［3］ Li M，Henry M. Complex signal processing for Coriolis mass flow metering in two-phase flow[J]. Flow Measurement & Instrumentation，2018，64：104-115.

［4］ Li M，Henry M P，Zhou F B，et al. Two-phase flow experiments with Coriolis mass flow metering using complex signal processing[J]. Flow Measurement and Instrumentation，2019，69(5)：101613.

［5］ Hemp J，Yeung H. Coriolis meters in two phase conditions[J]. IEEE Computing & Control Engineering，2003，14(4)：36.

［6］ Liu J Y，Wang T，Yan Y，et al. Predicting the output error of a Coriolis flowmeter under gas-liquid two-phase conditions through analytical modelling[C]//18th International Flow Measurement Conference. Lisboa，Portugal，2019：161254.

［7］ 赵玉琦. 基于科氏流量计的环状流测量模型研究[D]. 青岛：中国石油大学(华东)，2013.

Zhao Yuqi. Study on the Measurement Model of Annular Flow Based on the Coriolis Flowmeter[D]. Qingdao：China University of Petroleum(East China)，2013(in Chinese).

［8］ 李姗姗. 科氏流量计测量气液两相分层流的模型研究[D]. 青岛：中国石油大学(华东)，2013.

Li Shanshan. Research on the Model of Coriolis FlowMeter Measuring Gas-Liquid Two-Phase Stratified Flow [D]. Qingdao：China University of Petroleum(East China)，2013(in Chinese).

［9］ Liu R P，Fuent M J，Henry M P，et al. A neural network to correct mass flow errors caused by two-phase flow in a digital Coriolis mass flowmeter[J]. Flow Measurement and Instrumentation，2001，12：53-63(in Chinese).

［10］ 马龙博，张宏建，周洪亮，等. 基于 Coriolis 流量计和 SVM 的油水两相流质量流量测量的研究[J]. 高校化学工程学报，2007，21(2)：201-205.

Ma Longbo，Zhang Hongjian，Zhou Hongliang，et al. Mass flow measurement of oil-water two-phase flow based on Coriolis flow meter and SVM[J]. Journal of Chemical Engineering of Chinese Universities，2007，21(2)：201-205(in Chinese).

［11］ 侯其立. 批料流/气液两相流下科氏质量流量计信号处理和数字驱动方法研究与实现[D]. 合肥：合肥工业大学，2015.

Hou Qili. Study and Implementation of Signal Processing and Digital Drive Method for Coriolis Mass Flowmeter in Batch/Gas-Liquid Two-Phase Flow Measurement[D]. Hefei：Hefei University of Technology，2015(in Chinese).

［12］ Wang L J. Gas-liquid two-phase flow measurement using Coriolis flowmeters incorporating artificial neural network，support vector machine and genetic programming algorithms[J]. IEEE Transactions on Instrumentation and Measurement，2017：66(5)：852-868.

［13］ 乐 静. 科氏质量流量计测量两种特殊流量时的方法研究与实现[D]. 合肥：合肥工业大学，2019.

Le Jing. Research and Implementation of Coriolis Mass Flowmeter for Measuring Two Special Flow Rates[D]. Hefei：Hefei University of Technology，2019(in Chinese).

［14］ Meribout M，Shehzad F，Kharoua N，et al. Gas-liquid two-phase flow measurement by combining a Coriolis flowmeter with a flow conditioner and analytical Models[J]. Measurement，2020，163：107826.

［15］ Cortes C，Vapnik V. Support-vector networks[J]. Machine Learning，1995，20：273-297.

［16］ Drucker H，Burges C，Kaufman L，et al. Support vector regression machines[J]. Advances in Neural Information Processing Systems，1997，28(7)：779-784.

［17］ 周志华. 机器学习[M]. 北京：清华大学出版社，2016.

Zhou Zhihua. Machine Learning[M]. Beijing：Tsinghua University Press，2016(in Chinese).

［18］ 钱红兵，李艳丽. 一种基于凸包稀疏化与遗传算法优化的SVM算法[J]. 重庆大学学报，2021，44(1)：29-36.

Qian Hongbing，Li Yanli. A SVM algorithm based on convex hull sparsity and genetic algorithm optimization[J]. Journal of Chongqing University，2021，44(1)：29-36(in Chinese).

［19］ 魏鹏飞，樊小朝，史瑞静，等. 基于改进麻雀搜索算法优化支持向量机的短期光伏发电功率预测[J]. 热力发电，2021，50(12)：74-77.

Wei Pengfei，Fan Xiaochao，Shi Ruijing，et al. Short-term photovoltaic power generation forecast based on improved sparrow search algorithm and optimized support vector machine[J]. Thermal Power Generation，2021，50(12)：74-77(in Chinese).

［20］ 刘小生，章治邦. 基于改进网格搜索法的SVM参数优化[J]. 江西理工大学学报，2019，40(1)：5-9.

Liu Xiaosheng，Zhang Zhibang. Parameter optimization of support vector machine based on improved grid search method[J]. Journal of Jiangxi University of Technol-ogy，2019，40(1)：5-9(in Chinese).

［21］ 孟田华，卢玉和，丁少军，等. 基于SVM的温度预测回归模型[J]. 现代计算机，2020(20)：3-6，13.

Meng Tianhua，Lu Yuhe，Ding Shaojun，et al. Temperature prediction regression model based on SVM[J]. Modern Computer，2020(20)：3-6，13(in Chinese).

［22］ 程云芳，邱 榕. 基于粒子群-支持向量机(PSO-SVM)的苯储罐泄漏事故风险预测[J]. 火灾科学，2020，29(3)：190-198.

Cheng Yunfang，Qiu Rong. Risk prediction of benzene storage tank leakage accident based on particle swarm optimization-support vector machine(PSO-SVM)[J]. Fire Safety Science，2020，29(3)：190-198(in Chinese).

［23］ Wang L J，Yan Y，Wang X，et al. Input variable selection for data-driven models of Coriolis flowmeters for two-phase flow measurement[J]. Measurement Science and Technology，2017，28(3)：035305.

［24］ 李春辉. 基于ZYNQ的科氏流量计转换器新技术研究[D]. 天津：天津大学，2020.

Li Chunhui. Research on New Technology of Coriolis Flowmeter Converter Based on ZYNQ[D]. Tianjin：Tianjin University，2020(in Chinese).

Gas-Liquid Two-Phase Flow Measurement Based on Coriolis Flowmeters and PSO-SVM

Sun Lijun1, 2，Liu Yue1, 2，Tong Jielin3，Chen Shuiyuan1，Gao Jingyu1, 2

(1. School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China；2. Tianjin Key Laboratory of Process Measurement and Control，Tianjin 300072，China；3. Walsn Measurement and Control Technology Co.，Ltd.，Langfang 065009，China)

A Coriolis mass flowmeter can measure a single-phase flow with high accuracy. However，the measurement performance of the Coriolis flowmeter decreases，and the measurement error increases sharply under gas-liquid two-phase flow conditions. To improve the performance of Coriolis flowmeters and quantify the gas volume fraction(GVF) when measuring two-phase flows，this study performed gas-liquid two-phase flow experiments using a differential pressure transmitter with a GVF ranging from 0 to 30 %. The flow range of the tested Coriolis flowmeter is 0—1000kg/h. Measurement models of the mass flow and GVF based on the particle swarm optimization algorithm-support vector machine(PSO-SVM)were designed. The PSO algorithm improved the speed of model construction and prediction accuracy. The differential pressure can provide the flow pattern and GVF information，which was found to be a critical input variable of the models. The relative error of the mass flow correction，including this variable，is 1.5%，and the absolute error of GVF prediction is ±3%. However，the differential pressure measurement comes from the external differential pressure transmitter，which may lead to some problems such as inconvenient installation and space limit. Therefore，to achieve an integrated measurement，new dynamic variables from the Coriolis flowmeter itself were considered to replace the differential pressure with acceptable accuracy. With the result of experimental data analysis，another model without differential pressure was established. The mass flow variance was applied to replace the differential pressure for mass flow correction. In addition，a two-stage support vector machine(SVM) model structure was adopted for GVF prediction. The absolute deviation of the mass flow correction was used as an input variable for the GVF model to replace the differential pressure. Results show that the relative error of mass flow prediction is about ±2% and the absolute error of GVF prediction is ±3%. The differential pressure measurement can be replaced by internal measurement variables without losing much accuracy.

Coriolis flowmeter；gas-liquid two-phase flow；support vector machine(SVM)；particle swarm optimization(PSO) algorithm；gas volume fraction(GVF)

TH814

A

0493-2137(2022)10-1034-11

10.11784/tdxbz202109037

2021-09-27；

2021-11-30.

孙立军（1974— ），男，博士，副教授，sunlijun@tju.edu.cn.

刘 悦，2019234195@tju.edu.cn.

国家自然科学基金资助项目(62073240).

the the National Natural Science Foundation of China(No. 62073240).

(责任编辑：孙立华)