静止起步工况下驾驶性评价

蓝志宝 王 哲 蒋华梁 罗 旭

（1.上汽通用五菱汽车股份有限公司，广西 柳州 540057；2.武汉理工大学，湖北 武汉 430070）

0 前言

车辆驾驶性是指车辆对驾驶员采取的相关操作所做出的相应的动态响应，它反映了车辆的动态性能。目前，国内外评价车辆驾驶性的方法包括主观评价和客观评价。主观评价是驾驶评测师通过特定的驾驶方案给驾驶主观感受打分，打分结果会在很大程度上受主观感受的影响。客观评价是通过分析汽车行驶的原始数据，并结合所研究车辆选取合适的客观指标对车辆驾驶性进行分析。

针对主观评价，HYOSEONG 等人通过改变车内噪声的品质来探究主观评价结果的作用情况。杨家成等人提出用模糊层次分析法构建权重和离散系数，以验证试车员的评价能力。针对客观评价，黄伟等人通过计算主、客观权重设计了车辆蠕行工况驾驶性的综合权重优化模型，构建了更加完善的评估体系。莫易敏等人使用神经网络搭建了急加速工况的驾驶性评价模型，提高了预测的准确率。刘海江等人通过小波去噪的方式保留了原始数据中的有效成分，提高了客观评价指标的准确性。孙博等人采用动力总成台架模拟整车驾驶性评价，大大降低了试验成本。

该文选取车辆静止起步工况，利用BP 神经网络建立主观评价、客观评价之间的关系，用数据指标来弥补主观评价一致性差的问题。

1 起步工况客观评价指标

1.1 起步工况分析

起步工况是车辆在静止状态下通过驾驶员的一系列操作使车辆速度由0 km/h 加速到某个阈值的状态。在起步工况中，车辆的速度由0 km/h 加速到某个阈值，从工况角度分析，希望起步时间尽可能短，车的状态尽可能平稳，但当车辆突然改变状态时，会使加速度呈现一个从无到有的颠簸过程，这势必会影响驾驶员的舒适性。因此，需要从起步过程中的动态指标、驾驶的舒适性2 个方面对起步工况驾驶性进行分析。

车辆加速度的大小决定了起步时间的长短，而加速度的变化又会影响驾驶员对舒适性的直观感受，因此选取起步工况中的峰值加速度、最大变加速度、发动机转速正向超调量以及加速度颠簸等指标来评价车辆的运行情况。由于动力传动系统存在延迟性，当踩下加速踏板时，发动机转速、车速并不会瞬间变化，这也会给人体反馈机制带来不适，因此选取制动踏板释放延迟、响应延迟和动力丢失等指标以及加速度信号综合评价车辆起步工况的动态性和驾驶舒适性，相关指标见表1。

表1 驾驶性客观评价指标

1.2 起步工况指标说明

用图形展示表1 中的性能指标，如图1、图2 所示。

图1 踏板释放延迟与车速变化关系

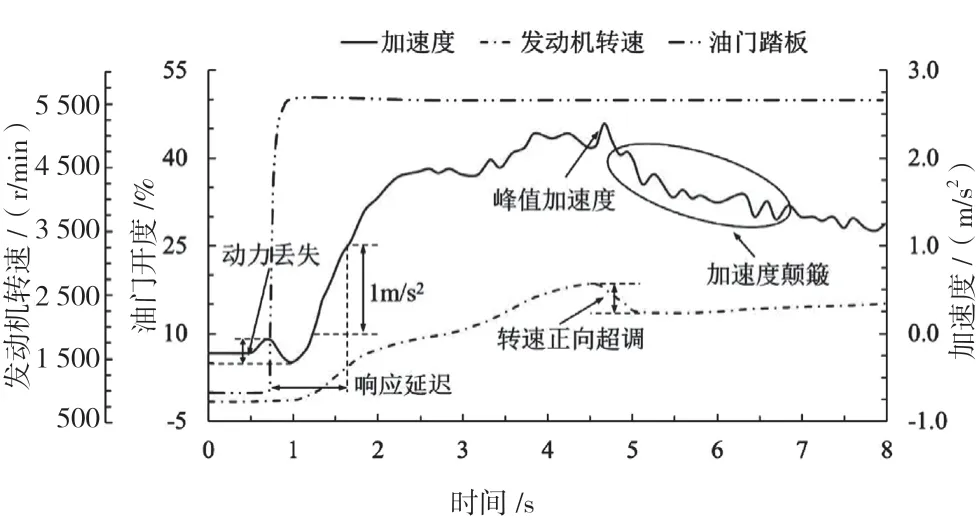
图2 发动机转速与加速度

客观评价指标的具体含义如下：1） 响应延迟。响应延迟是指油门踏板开度变化与速度变化之间的延迟时间，将踩下油门踏板至加速度达到1 m/s所经历的时间记为响应延迟（越大表示车辆传动效率越低，动态性不好），如公式（1）所示。2） 峰值加速度。峰值加速度是整个工况中加速度的最大值，如公式（2）所示。3） 最大变加速度。最大变加速度是加速度变化最大的位置，在图2 中为加速度曲线斜率最大的点，如公式（3）所示。4） 加速度冲击。加速度冲击是给定区间加速度峰值与之后第一个波谷的加速度差值，如公式（4）所示。5） 加速度颠簸。将加速度达到峰值后的5 个加速度冲击记为加速度颠簸。6） 加速度扰动。受外界因素的影响，汽车运行过程中的加速度曲线会在理想范围内波动，加速度扰动采用平均值（）、均方根（）以及振动剂量值（）3 个指标来表述。其中，平均值、均方根以及振动剂量值如公式（5）～公式（7）所示。7） 制动踏板释放延迟。以完全释放踏板为时间节点，将车辆加速度增量超过0.1 m/s所用的时间作为标记，如果此时已超过0.1 m/s，则该项指标记为0。8） 油门踏板响应延迟。油门踏板响应延迟是指油门踏板开度开始大于0%至车辆加速度高于1.0 m/s时所用的时间。9） 转速正向超调量。转速正向超调量是指在起步工况中发动机转速的最大值与平稳转速的差值，正常起步过程超调量不宜过大。10） 动力丢失。动力丢失是指在油门开度变化的瞬间，因发动机进气量的改变而导致阻力增加，从而出现加速度突然下降的现象，并用踩下油门踏板前后加速度冲击值来衡量。

式中：t为响应延迟时间，s；t为加速度到达1 m/s的时刻，s；t为踩下油门踏板的时刻，s。

式中：为峰值加速度，m/s；为起步工况的时刻，s；为该时刻所对应的车速，m/s。

式中：为最大变加速度，m/s；为起步工况的时刻，s；为该时刻所对应的车辆加速度，m/s。

式中：Δ为加速度冲击，m/s；为加速度峰值，m/s；a为对应时间后加速度曲线的第一个波谷值，m/s。

式中：a为加速度平均值，m/s；a为第个加速度信号值，m/s；为加速度信号个数。

式中：a为均方根，m/s。

式中：a为振动剂量值，m/s。

2 驾驶性评价模型

2.1 神经网络类型选择及原理

在评估车辆起步工况的驾驶性时，需要通过大量的试验数据寻找驾驶员主观评价等级与汽车客观工况指标之间的联系。神经网络系统在这方面具有突出的优势，当处理2 个变量的关系时，可以通过大量的训练模型来构建两者的预测关系。由于BP 神经网络系统具有很强的映射关系，因此选用该系统来搭建起步工况的驾驶性评价模型。

BP 神经网络是一种信号向前传递、误差反向传递的多层前馈网络，主要包括输入层、隐含层及输出层。输入信号经过输入层、隐含层以及输出层的处理得到输出值，与期望值进比较，将得到的误差反馈到每层，从而对系统进行校正，其网络拓扑图如图3 所示。

图3 BP 神经网络拓扑图

2.2 驾驶性评价模型搭建

根据需求对已选取的BP 神经网络系统进行设计，最终要确定神经网络的层数和节点数。神经网络的层数由隐藏层的数量决定，从理论上来说，层数越深其拟合效果越理想，但是层数过深就会存在过拟合和训练难度增加的缺点。考虑驾驶性的主观评价、客观评价所涉及的变量个数有限，因此选用相对简单的单隐含层设计。

由第2 节的9 个驾驶性的客观评价指标和1 个评分指标可知，神经网络的输入节点为9，输出节点为1。同时，根据公式（8）可以得出最终的模型结构为9-6-1。

式中：和分别为输入节点数和输出节点数；为隐含层节点数；为0～10 的常数。

利用MATLAB 软件中的Neural Fitting 工具箱搭建驾驶性预测模型（并选用Levenberg-Marquardt 算法）。搭建的起步工况驾驶性评价预测模型流程如图4 所示。

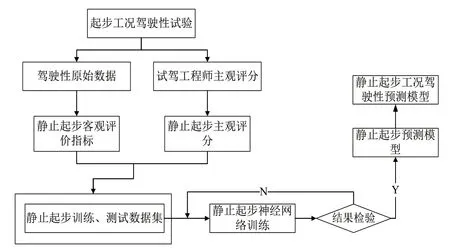
图4 静止起步工况驾驶性预测模型构建流程

3 实车试验验证

3.1 驾驶性试验与数据采集

该试验选用某企业的3 款SUV 车型，分别为搭载CVT变速箱的V、搭载AT 变速箱的V以及搭载DCT 变速箱的V。每款车都是企业用于测试的车辆，并已过磨合期，各项指标符合要求，如图5 所示（通过AVL-Drive 数据采集仪收集实车试验所需的数据）。车辆在平直的公路上静止，松开制动踏板时开展2 种试验：1） 以25%油门开度使车辆从0 km/h 加速到10 km/h 的稳定车速。2）以50%油门开度使车辆从0 km/h 加速到10 km/h的稳定车速。在松开制动踏板前开始采集数据（每辆车各140组原始数据，共计420 组原始数据）。

图5 实车试验现场图

3.2 预测模型训练

对420 组原始数据进行整理，从而得到客观评价指标的量化值，并从每组数据中随机选出100组数据用于神经网络的训练方案。考虑BP 神经网络各层节点的相互影响，因此需要消除因量纲不同而带来的实验结果的差异，该文选用归一化的方式进行处理，使各个指标可以进行加权等运算，以对驾驶性进行综合评价。归一化方法有最大最小法和平均数方差法，最大最小法的函数如公式（9）所示。

式中：为归一化后数据；x为原始数据；为数据序列的最小值；为数据系列的最大值。

平均数方差法的函数如公式（10）所示。

式中：、、x和x分别为数据序列的最小值、最大值、平均值和方差。

将样本数据按照14 ∶3 ∶3 的比例划分为训练集、验证集以及测试集，并利用MATLAB 软件中的神经网络工具箱进行模拟训练。在训练过程中，值的收敛情况如图6 所示。预测模型一共训练了13 步，在训练过程中各数据集值均逐步降低，在第8 步值达到最低（0.003 039 6）。

图6 起步工况模型训练过程loss 值收敛图

求取2 个预测模型训练过程中各数据集预测值与真实值间的误差，误差分布情况如图7 所示。

图7 起步工况模型训练误差分布图

预测模型的误差分布在-0.132 7～0.202 5，最小误差绝对值为 0.008 459，最大负值误差由训练集数据产生，最大正值误差由训练集及验证集数据产生。由此可见，通过该模型进行预测的误差绝对值小于0.25，误差表现良好。

用线性拟合方案探寻预测值与真实值之间的相关性，结果如图8 所示。训练集、验证集、测试集以及总的相关系数分别为0.994 0、0.993 9、0.979 0 以及0.992 7。预测值与真实值间的相关系数大于0.95，说明预测值与真实值的结果相关度很高，预测值在一定程度上能反映真实值的大小。

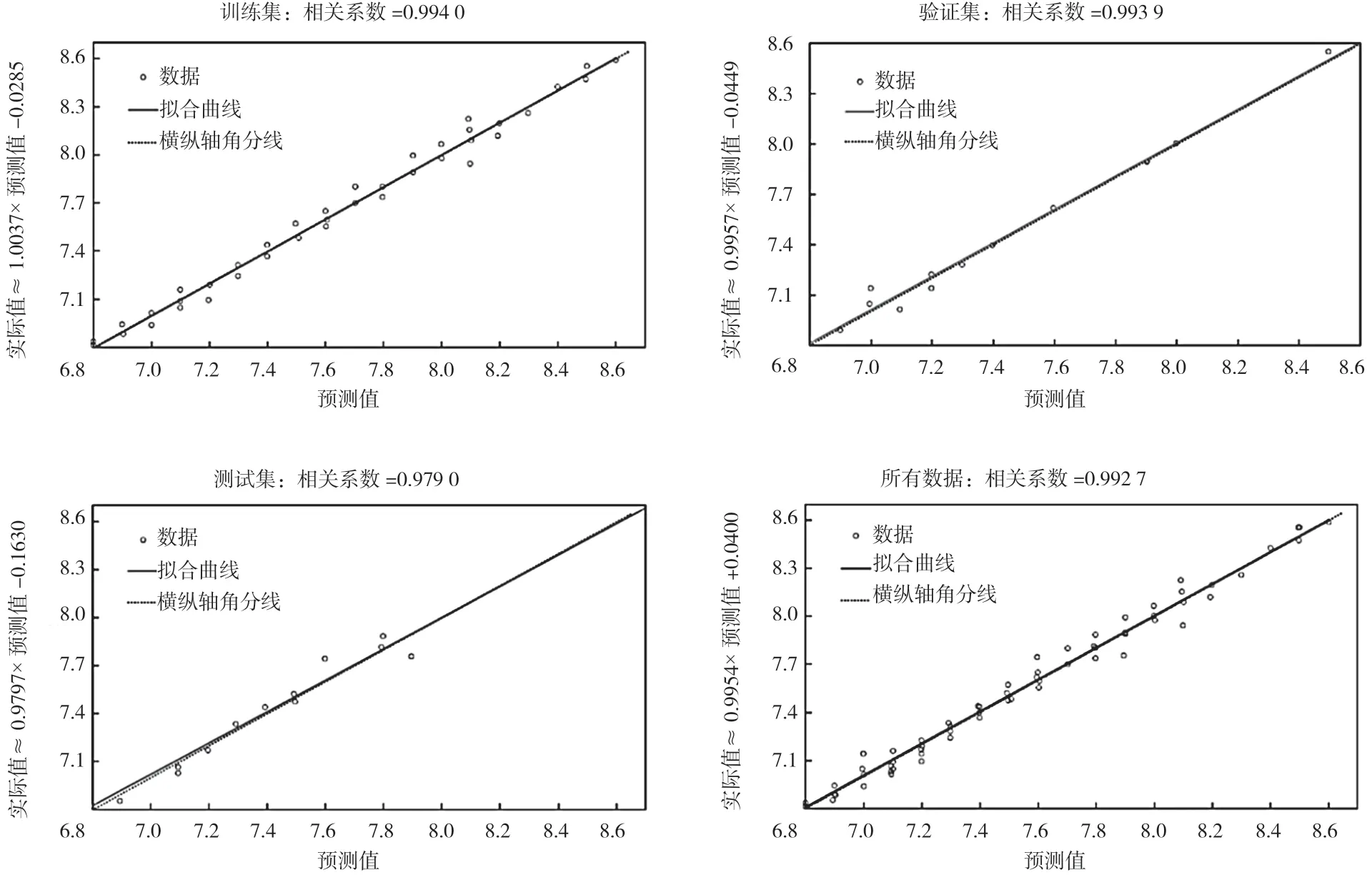
图8 起步工况模型训练各数据集线性相关度

3.3 预测模型准确率验证

为了验证训练集测试的模型的准确性，现从剩余的试验数据中选取20 组进行验证试验。

为了验证加速工况中2 个预测模型在未知实际输出值情况下的预测能力，在140 组数据集剩余的40 组数据中随机选取20 组数据对模型进行检验，结果见表2。

由表2 可知，误差最小值为第7 组的0.002，最大值为第5 组的0.440。美国驾驶性评分标准SAEJ1441 将驾驶性区分为5 个等级，见表3。

现以误差小于0.5 作为合格率评定指标，则该起步工况驾驶性评价预测模型的合格率为100%。表明对试验车辆起步工况来说，BP 神经网络预测模型有很高的精度，可以为驾驶性的主观评价、客观评价提供一种可靠的方法。

4 结语

该文对静止起步工况中车辆运行的各项速度、加速度以及延迟性等指标进行测定和分析，借助BP 神经网络强大的映射关系，将车辆的这些指标作为衡量评判驾驶性的标准，以解决由驾驶性主观评价所带来的一致性差和难以复现的问题，并通过试验验证了模型的准确性。但是由于所选车辆和所选工况的特殊性，因此不能保证该方案的全局适用性，还需要进一步对预测模型的准确率进行验证。