500 kV同塔双回输电线路感应电压和感应电流建模分析
唐浩龙,樊 艳,冯千秀,牟婷婷
(中国电力工程顾问集团西南电力设计院有限公司,四川 成都 610021)
0 引 言
随着中国电力行业的迅猛发展,超高压、特高压输变电工程不断增多,众多变电站、换流站之间的输电线路分布也越来越密集。为了解决输电线路通道走廊受限问题,节省工程总投资,同塔双架设的输电线路形式成为了目前的主流趋势。线路同塔双回架设经济方便,优势明显,但也为后期线路的检修、维护工作带来了新的难题。
由于采用同塔双回结构,导致两回线路之间的相间距离大幅减小,使得耦合线路作用进一步加强。当其中一回线路运行而另一回线路需要停电检修时,正常运行的线路会在停运线路上感应出较大的电压和电流,给检修人员和运行设备带来安全隐患。文献[1]研究了110 kV同塔双回线路感应电压和感应电流对人体的危害。文献[2-3]研究了不同电压等级输电线路同塔架设时各回路之间感应电压和感应电流的变化规律,并对线路接地开关参数的选择提出了要求。文献[4-5]对某330 kV和500 kV同塔双回输电线路下平行运行的380 V线路进行了感应电压、感应电流的仿真计算,推荐了检修作业方式。文献[6]仿真计算了±800 kV、±500 kV 直流线路运行时,在邻近直流线路的1000 kV特高压同塔双回线路上产生的感应电压。关于同塔双回输电线路感应电压、感应电流的研究目前已较多,但对其影响因素的多变量拟合和感应电压、感应电流简易估算的研究却鲜有报道。
为了准确分析同塔双回输电线路感应电压、感应电流的变化规律和影响因素,下面利用电磁暂态仿真软件ATP-EMPT建立了500 kV同塔双回架空输电线路仿真模型,计算分析了线路长度、输送功率、运行电压和土壤电阻率对感应电压和感应电流的影响,并利用混合差分进化-粒子群优化算法对上述影响因素进行拟合,给出了感应电压、感应电流的多元拟合公式。
1 感应电压和感应电流理论分析
同塔双回输电线路当一回线路正常运行、另一回线路停运时,停运线路上会产生静电耦合和电磁耦合作用[7],两条线路间的耦合如图1所示。其中,UA、UB、UC为正常运行线路的三相电压;IA、IB、IC为正常运行线路的三相电流;CAa、CBa、CCa和MAa、MBa、MCa分别为正常运行线路A、B、C三相与停运线路a相间的单位长度互电容和互电感;Ca0和Ma0分别为停运线路a相单位长度对地电容和对地电感;L为线路长度。
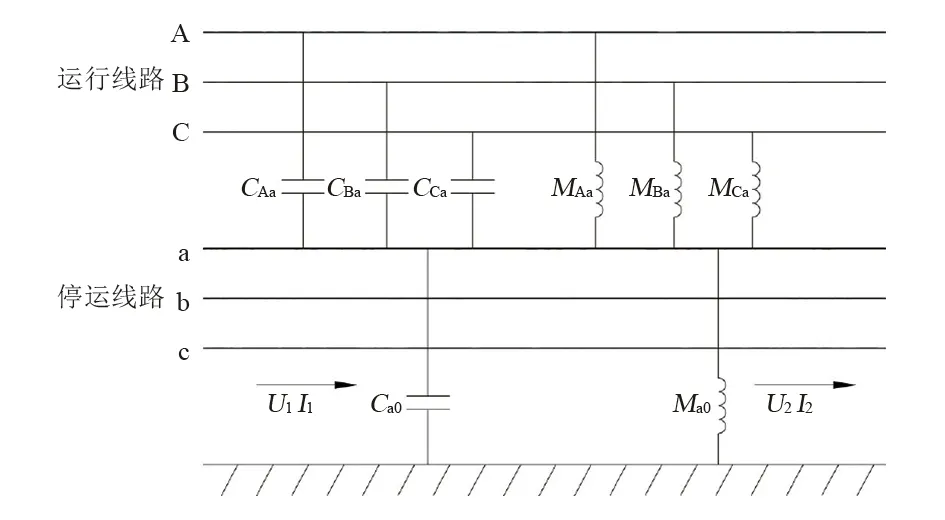
图1 同塔双回线路耦合
对停运线路a相任意位置列出感应电压、感应电流计算方程为:
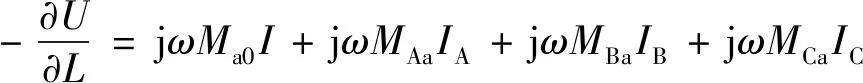
(1)
(2)
由于正常运行线路三相电压电流相角差为120°,代入式(1)和式(2)得:
U2=U1cos(γL)-jI1Zcsin(γL)+
(α/γ2)UA[1-cos(γL)]-j(M/Ma0)ZcIAsin(γL)
(3)
(4)
其中:
(5)
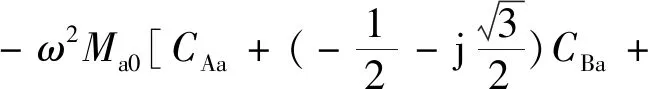
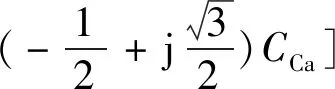
(6)
(7)
(8)
式中:U1、I1为停运线路首端电压、电流;U2、I2为停运线路末端电压、电流;γ为线路的传输参数;α为等效电容;M为等效电感;Zc为波阻抗。
1)当停运线路两端均不接地时,停运线路中感应电流I1=I2≈0。且对于一般线路,有γL<<1,则有
(9)
2)当停运线路一端接地、一端不接地时,设末端接地,即I1=0,U2=0,则有
|U1|≈|jωL(MAaIA+MBaIB+MCaIC)|
(10)
|I2|≈|jωL(CAaUA+CBaUB+CCaUC)|
(11)
3)当停运线路两端均接地时,有U1=0,U2=0,则
I1≈I2≈-(MAaIA+MBaIB+MCaIC)/Ma0
(12)
2 仿真计算
2.1 计算模型
所研究的输电线路采用同塔双回结构,研究基准参数设定如下:线路长度为60 km,线路运行额定电压为525 kV,额定输送功率为1000 MW,导线规格型号为4×JL/LB20A-400/50,分裂间距为400 mm;架空地线采用JLB20A-120;工频接地电阻取10 Ω,土壤电阻率取100 Ω·m。同塔双回杆塔结构如图2 所示。
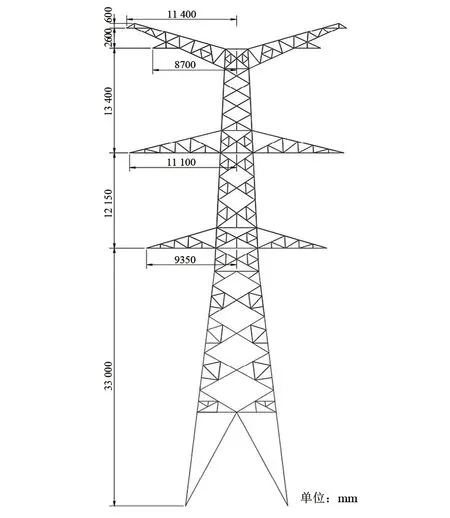
图2 500 kV同塔双回杆塔结构
利用电磁暂态仿真软件ATP-EMTP 中的架空线路LCC 模块建立同塔双回PI仿真模型,该模型适用于长度不超过300 km的架空输电线路的计算[8],且系统运行参数、线路和杆塔参数均可采用详细参数[9]。
2.2 静电感应电压计算
当一回线路正常运行,另一回线路停止运行,且停运线路两端均不接地时,设定运行线路输送功率为1000 MW,运行电压为525 kV。通过上述仿真模型,计算得到停运线路上产生的最大感应电压为34.23 kV(幅值),静电感应电压三相波形如图3所示。
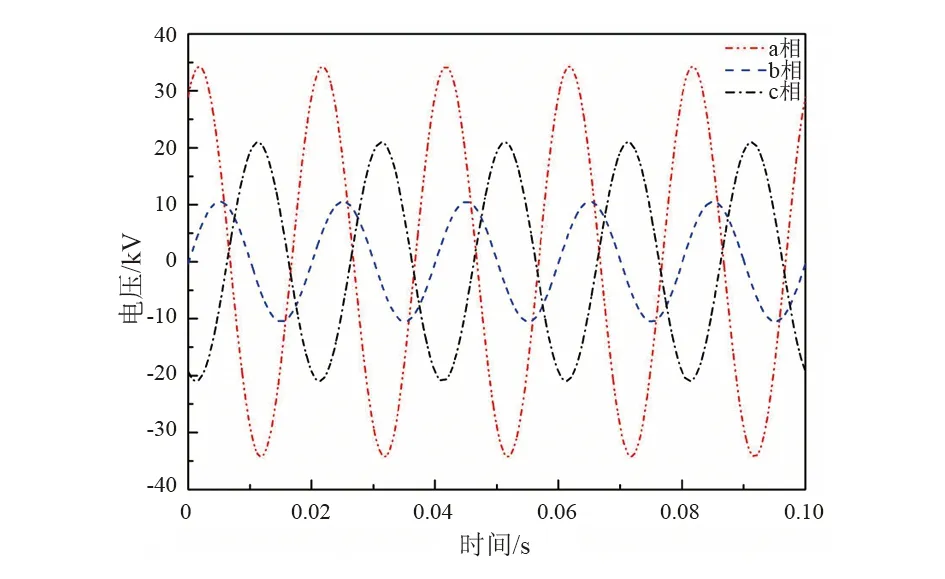
图3 停运线路静电感应电压
2.3 电磁感应电压与静电感应电流计算
当一回线路正常运行,另一回线路停止运行,且停运线路一端接地、一端不接地时,设定运行线路输送功率为1000 MW,运行电压为525 kV。通过计算得到停运线路上产生的最大电磁感应电压为9.44 kV(幅值),最大静电感应电流为8.08 A(幅值),电磁感应电压与静电感应电流三相波形如图4和图5所示。
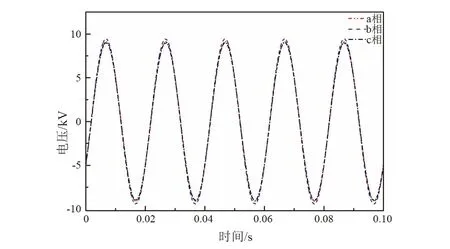
图4 停运线路电磁感应电压
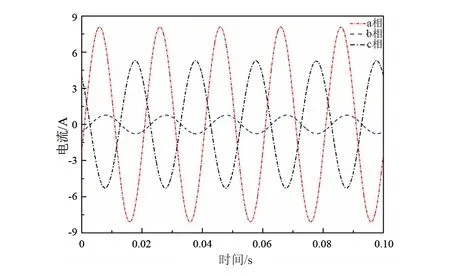
图5 停运线路静电感应电流
2.4 电磁感应电流计算
当一回线路正常运行,另一回线路停止运行,且停运线路两端均接地时,设定运行线路输送功率为1000 MW,运行电压为525 kV。通过上述仿真模型,计算得到停运线路上产生的最大电磁感应电流为288.42 A(幅值),电磁感应电流三相波形如图6所示。

图6 停运线路电磁感应电流
3 感应电压和感应电流影响因素分析
为了研究不同运行工况下感应电压与感应电流的大小,以停运线路a相为例,分别以线路长度、输送功率、运行电压和土壤电阻率为控制变量进行分析。设定基准线路长度为60 km,输送功率为1000 MW,运行电压为525 kV,土壤电阻率为100 Ω·m。对某一影响因素进行分析时,保持其他影响因素参数一致。
3.1 线路长度
为了研究线路长度对感应电压和感应电流的影响,保持其他参数不变,设定线路长度分别为20 km、40 km、60 km、80 km和100 km,利用仿真模型对感应电压和感应电流进行计算,结果如图7所示。由图7可知,线路长度对静电感应电压影响较小;电磁感应电压和静电感应电流随线路长度的增加而增大,近似成正比关系;电磁感应电流随线路长度增加而变小,但逐渐趋于平缓。
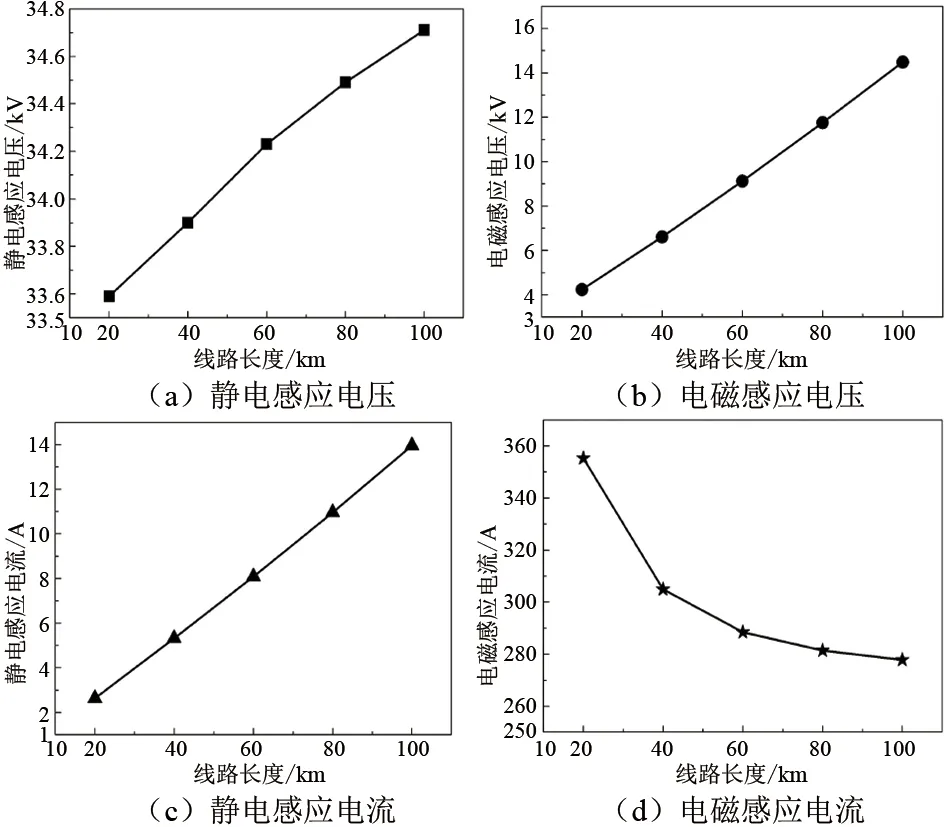
图7 线路长度对感应电压和感应电流的影响
3.2 输送功率
为了研究输送功率对感应电压和感应电流的影响,保持其他参数不变,设定输送功率分别为500 MW、1000 MW、1500 MW、2000 MW和 2500 MW,利用仿真模型对感应电压和感应电流进行计算,结果如图8所示。由图8可知,静电感应电压和静电感应电流随输送功率的增加而增大,但二者整体变化幅度均较小;电磁感应电压和电磁感应电流随输送功率的增加而显著增大,近似成正比关系。
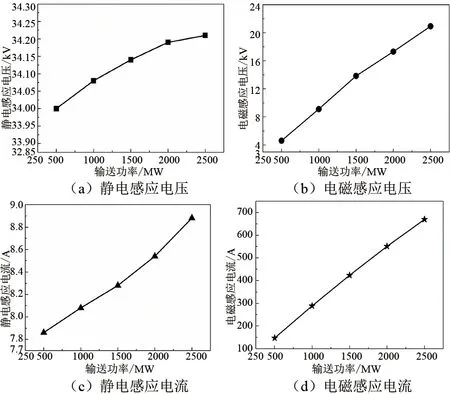
图8 输送功率对感应电压和感应电流的影响
3.3 运行电压
为了研究运行电压对感应电压和感应电流的影响,保持其他参数不变,设定运行电压分别为505 kV、515 kV、525 kV、535 kV和545 kV,利用仿真模型对感应电压和感应电流进行计算,结果如图9所示。由图9可知,静电感应电压、电磁感应电压、静电感应电流和电磁感应电流均随运行电压的增加而增大,4项均近似成正比关系。
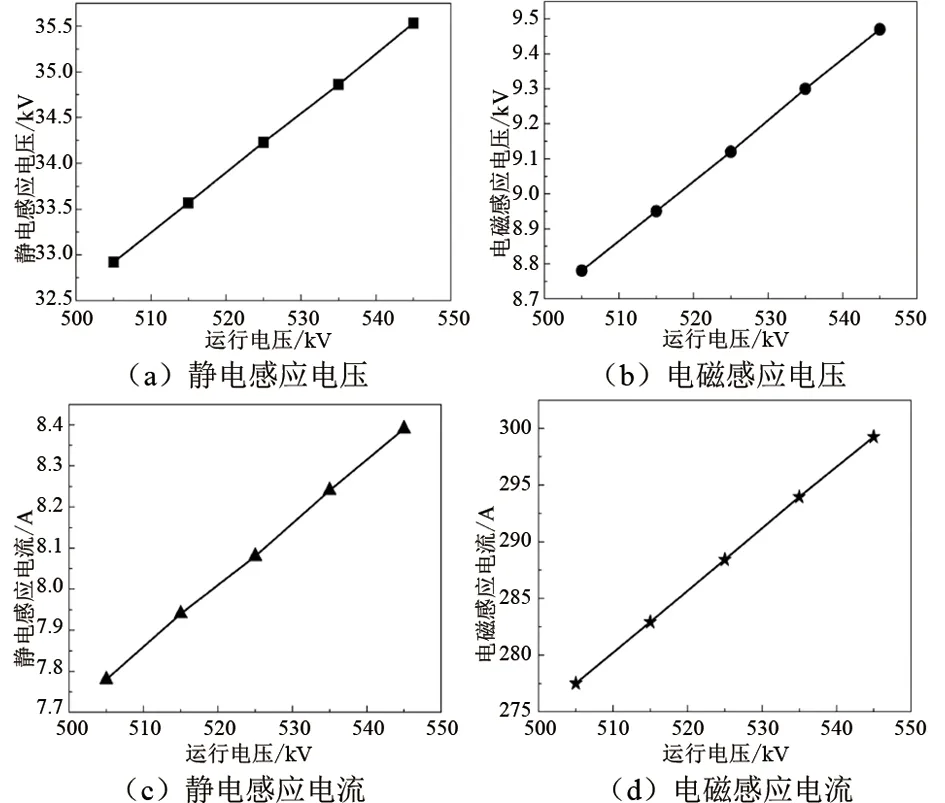
图9 运行电压对感应电压和感应电流的影响
3.4 土壤电阻率
为了研究土壤电阻率对感应电压和感应电流的影响,保持其他参数不变,设定土壤电阻率分别为10 Ω·m、50 Ω·m、100 Ω·m、200 Ω·m和 500 Ω·m,利用仿真模型对感应电压和感应电流进行计算,结果如图10所示。由图10可知,静电感应电压随土壤电阻率的增加而减小,静电感应电流随土壤电阻率的增加而增大,但二者变化极小;电磁感应电压和电磁感应电流随土壤电阻率的增加而增大。
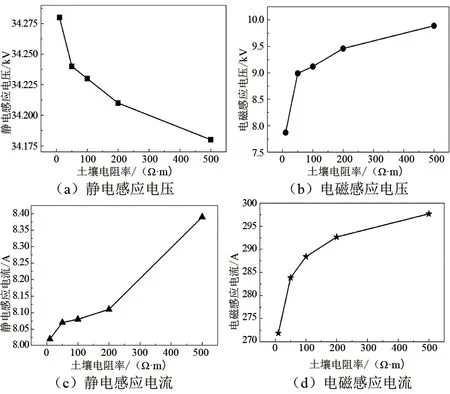
图10 土壤电阻率对感应电压和感应电流的影响
4 感应电压和感应电流多元拟合分析
根据前面可知,同塔双回输电线路一回运行、一回停运时,停运线路上感应电压和感应电流与线路长度、输送功率、运行电压和土壤电阻率都有一定的关系。为了明确该多变量对应关系,利用混合差分进化-粒子群优化算法对其进行拟合,该算法通过使用粒子群优化算法来加快收敛速度,并使用差分进化算法来增加种群的多样性,可以较好地得到全局最优解,实现较优拟合。
根据前面仿真数据,首先对各单变量进行初步拟合,以此确定最优的函数结构。假设静电感应电压为Us,电磁感应电压为Um,静电感应电流为Is,电磁感应电压为Im,线路长度为L,输送功率为P,运行电压为U,土壤电阻率为λ。经拟合分析,多变量函数具体可描述如下:
(13)
式中,a0~a4、b0~b4、c0~c4和d0~d4为待求参数。
利用Matlab软件,基于混合差分进化-粒子群优化算法确定上述各值,计算结果如表1所示。
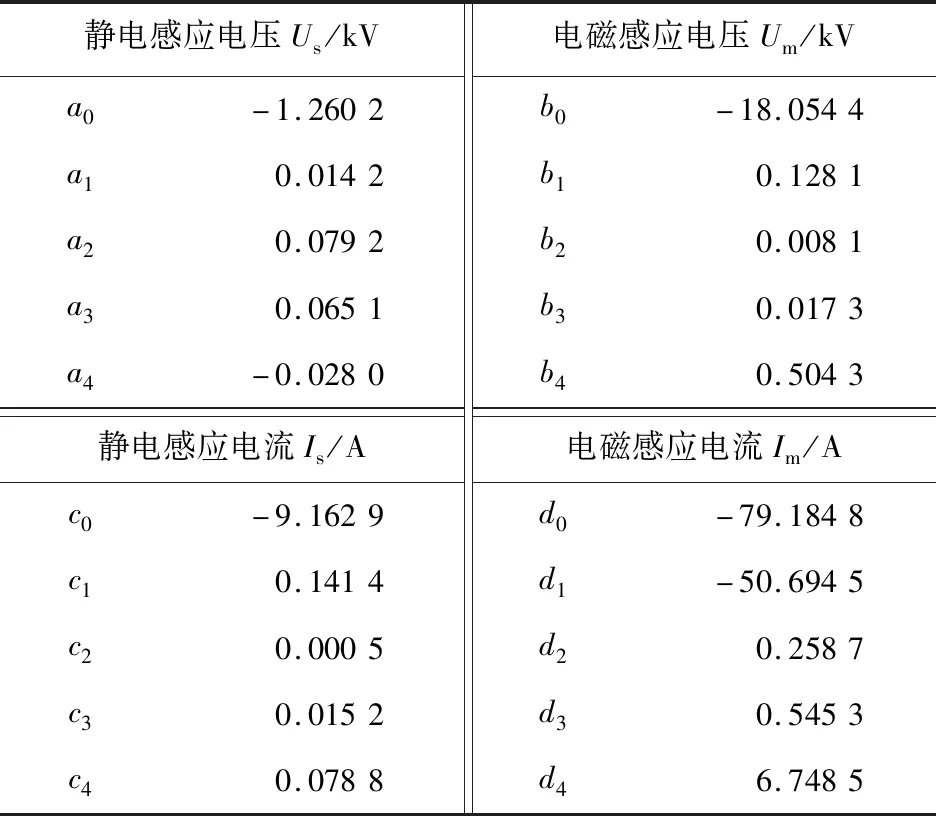
表1 待求参数结果
为了验证拟合公式的准确性,选取相同工况下的仿真输入数据代入拟合式(13)进行计算,并将计算结果与仿真结果进行对比,结果见表2。
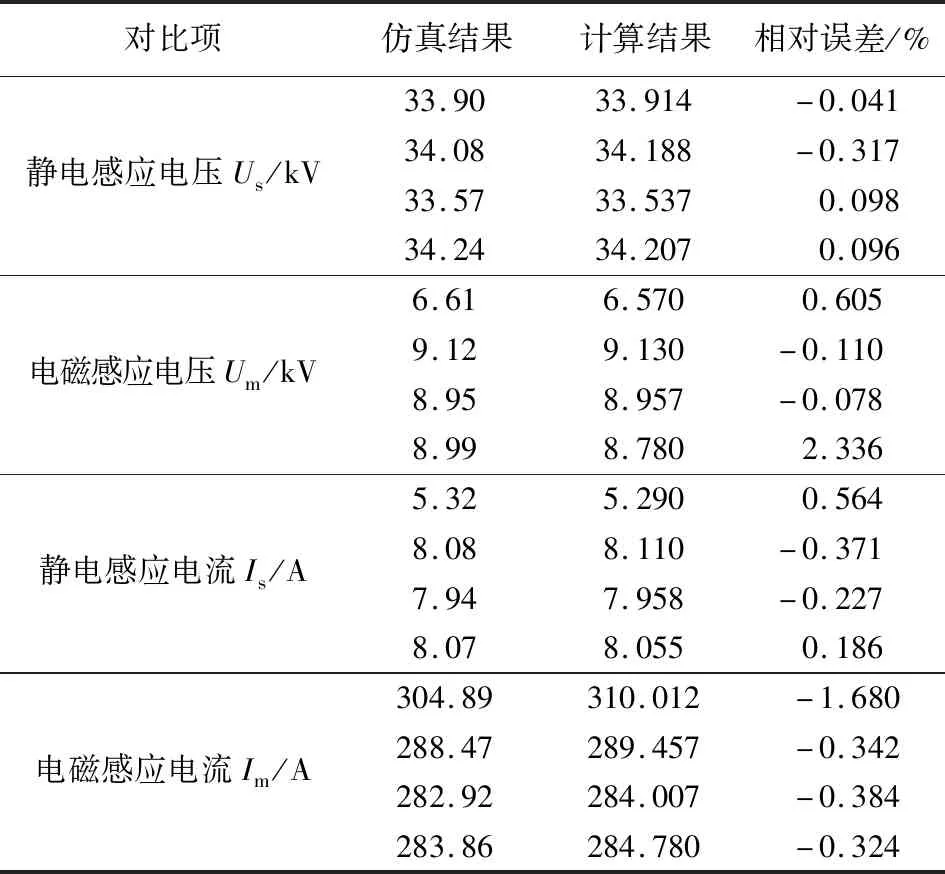
表2 仿真结果与拟合结果对比
由表2可知,静电感应电压仿真结果与拟合公式计算结果最大相对误差为0.317%,平均相对误差为0.138%;电磁感应电压仿真结果与拟合公式计算结果最大相对误差为2.336%,平均相对误差为0.782%;静电感应电流仿真结果与拟合公式计算结果最大相对误差为0.564%,平均相对误差为0.337%;电磁感应电流仿真结果与拟合公式计算结果最大相对误差为1.68%,平均相对误差为0.683%。通过上述4项对比发现,拟合公式计算结果与仿真结果平均相对误差均在1%以内,吻合程度较高,验证了拟合公式的准确性,为后续工程感应电压、感应电流的简易快速估算提供了参考。
5 结 论
通过对500 kV同塔双回输电线路感应电压、感应电流进行研究,得到以下结论:
1) 当同塔双回线路一回运行、一回停运时,在基准设定参数下,停运线路上产生的最大静电感应电压为34.23 kV,最大电磁感应电压为9.44 kV,最大静电感应电流为8.08 A,最大电磁感应电流为288.42 A。
2) 电磁感应电压和静电感应电流与线路长度近似成正比关系,电磁感应电流随线路长度增加而变小,但逐渐趋于平缓;电磁感应电压和电磁感应电流随输送功率成正比关系显著增加,静电感应电压和静电感应电流随输送功率变化较小;感应电压和感应电流均随运行电压增加而增大;土壤电阻率增大使得电磁感应电压和电磁感应电流有一定的增加,对静电感应电压和静电感应电流影响不大。
3) 感应电压、感应电流拟合公式计算结果与仿真结果吻合较好,平均相对误差均在1%以内,验证了拟合公式的准确性,为后续工程感应电压、感应电流的简易快速估算提供了一定参考。

