计及新能源不确定性的新能源场站与储能电站分布式协同优化

吴晓刚，吴新华，季青锋，马明玉，李高俊杰

（1.国网浙江省电力有限公司丽水供电公司，浙江 丽水 323000；2.武汉大学 电气与自动化学院，武汉 430072）

0 引言

近年来，以分布式电源为代表的新能源发展十分迅速，预计到2030 年我国分布式电源并网装机总容量将达到130 GW。随着我国“双碳”目标的提出，未来我国新能源装机容量势必大幅增加，其出力过程中的不确定性对电网运行造成的不良影响将日益凸显，新能源消纳问题亟待解决。

储能技术作为能源领域的一项重要技术，是解决新能源消纳问题的有效措施。现阶段大量学者已对储能参与新能源消纳开展了诸多研究。文献［1］针对含大规模风电的电力系统，引入机会约束，建立储能系统优化配置模型，采用改进灰狼算法得到储能最优配置方案。文献［2］提出一种提高配电网对新能源消纳能力的储能集群控制策略，既可以促进新能源消纳，又兼顾了系统运行的经济性。文献［3-5］计及风光消纳目标和热网储热特性，建立以成本最小化为目标的优化模型，有效地促进了新能源消纳。文献［6］建立了以弃风量最少为目标的风储能协调集中式优化模型，通过鲁棒优化算法求得最优解。文献［7］计及弃风成本、弃光成本和储能投资成本，建立了风光综合消纳的储能优化配置混合整数线性规划模型。文献［8］建立了上层以储能调频成本最小为目标、下层以调压效果最优为目标的双层优化模型，利用粒子群优化算法求解，证明该模型在利用储能调压的同时促进了新能源的消纳，充分挖掘了储能的应用潜力。文献［9］针对风电供给与负荷需求不匹配造成的能源浪费问题，提出了多家风电场联合的共享储能协同运行模式，通过仿真证明了共享储能的可行性，极大地促进了风电消纳。文献［10-11］计及风电出力的波动性以及储能的自身约束，建立风储联合的优化模型，得到储能容量的合理配置，有效提高了风电场的经济性。文献［12］考虑光伏消纳率，建立储能容量与功率配置的优化模型，并提出最优的储能规划方案。文献［13］计及风光出力不确定性，以运行成本最低为目标建立配电网的分布式优化模型，对配电网采用ADMM（交替方向乘子算法）进行分区优化，并通过仿真验证了调度策略的经济性。文献［14］考虑新能源出力波动性，建立配网侧与储能侧的分布式优化模型，采用ADMM求解，实现了主网购电费用最低与调度成本最小。文献［15］结合新能源与储能等资源的特点，建立双层分布式优化调度模型，该模型在保证电压质量的同时提高了新能源的消纳水平，但求解较为复杂。文献［16］以光伏与用户侧储能为对象建立分布式鲁棒优化模型，研究配电网与用户的能量交互，仿真结果表明该模型能有效地促进光伏消纳。

针对储能参与新能源消纳的分布式优化问题，本文提出计及新能源场站与储能电站分布自治决策特点的分解协同机制，采用基于ADMM的新能源场站-储能电站分布式协同优化算法，以储能充、放电功率为共享变量，通过少量多次的信息迭代，得到计及新能源不确定性的储能最优充、放电策略。最后，结合实际场景运行数据对比集中式算法与分布式协同算法的计算结果，对本文所提算法在解决新能源场站与储能电站间协同优化问题时的有效性和适用性进行验证。

1 新能源场站与储能电站的集中式优化模型

本文提出的基于ADMM的新能源场站与储能电站分布式协同优化模型是在集中式优化模型的基础上推导和分解得到的，且在算例中将其与集中式算法对比，因此，本节首先基于集中式调度的思想建立新能源场站与储能电站集中式优化模型。此时认为新能源场站与储能电站完全信息交互，可以实时获取对方的运行状态。两者同属于一个利益主体，作为一个整体来参与新能源的消纳，由调度部门统一制定储能充、放电计划。

1.1 目标函数

为了促进新能源的消纳，以发电机组出力和储能充、放电功率为决策变量，以弃风成本、弃光成本、储能的运行成本和机组的出力成本最小化为优化目标，即：

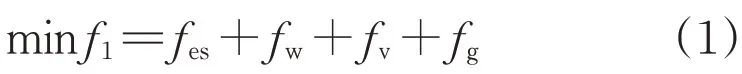
式中：f1为总成本；fes为储能运行成本；fw为弃风成本；fv为弃光成本；fg为机组运行成本。

1）储能运行成本fes来源于储能充、放电损耗，此处通过单位运行成本系数将该损耗转化为成本形式：

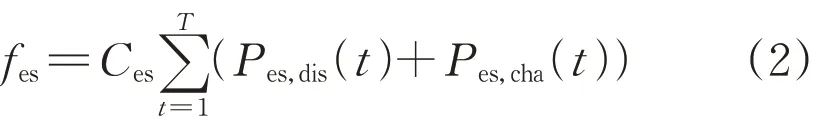
式中：Ces为储能电站单位运行成本系数；Pes，dis(t)为t时段储能放电功率；Pes，cha(t)为t时段储能充电功率；T为1个调度周期内的总时段数。

2）弃风成本fw和弃光成本fv分别为：

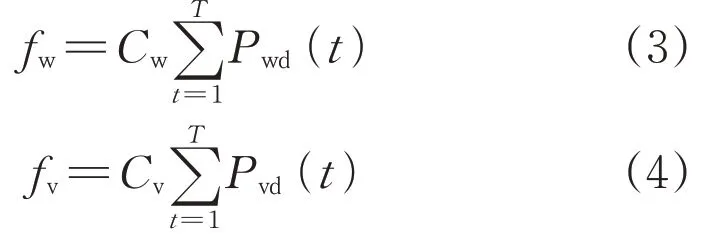
式中：Cw为单位弃风惩罚成本；Pwd(t)为t时段弃风功率；Cv为t时段单位弃光惩罚成本；Pvd(t)为t时段弃光功率。

3）机组运行成本fg为：

式中：Cg为发电机组单位出力成本；Pg(t)为t时段发电机组功率；a和b为机组出力成本拟合系数。

1.2 约束条件

上述优化目标需满足以下约束条件：功率平衡约束，机组出力约束，储能充、放电约束，荷电量约束，系统潮流约束。

1）功率平衡约束为：

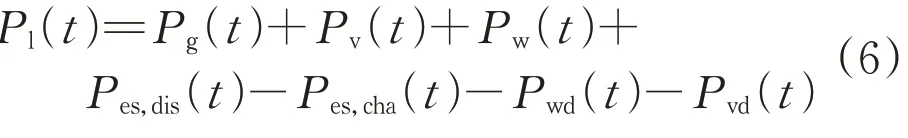
式中：Pl(t)为t时段负荷功率；Pw(t)为t时段风电功率；Pv(t)为t时段光伏发电功率；Pes，cha(t)和Pes，dis(t)分别为t时段储能充电功率和放电功率。

2）储能充、放电约束为：

3）储能荷电量约束为：

式中：Ses(t)为t时段储能装置能量状态；σes为储能装置自损率；ηes，cha和ηes，dis分别为充电效率和放电效率；Ses，max和Ses，min分别为储能装置能量状态上限和下限。

另外，储能设备在1个调度周期结束和开始时储存的能量应相同，该约束表示为：

4）机组出力约束为：

5）系统直流潮流约束为：

式中：Pi为节点i有功功率；Bij为线路ij的电纳；Pij为线路ij的潮流功率；θi为节点i相角；Xij为线路ij的电抗。

2 基于ADMM 的新能源场站与储能电站分布式协同优化模型

集中式优化方法依赖于储能电站与新能源场站间数据信息的完全交互，由同一个调度中心下发指令，而在实际电力系统中储能电站与新能源场站并不总是属于同一利益主体，各主体之间部分信息需要保密，不能进行完全的信息交互。为避免这一问题，本章针对新能源场站与储能电站的多主体决策特点，利用ADMM建立储能电站与新能源场站的分布自治决策和协同优化模型［17］。

2.1 分解协同机制

新能源场站与储能电站分布式协同优化的核心思想如图1所示。分别构建耦合共享变量的新能源与储能决策主体的优化模型，通过新能源与储能决策主体间少量多次的信息传递与优化迭代计算，达到新能源与储能自治决策、协同优化的目的。

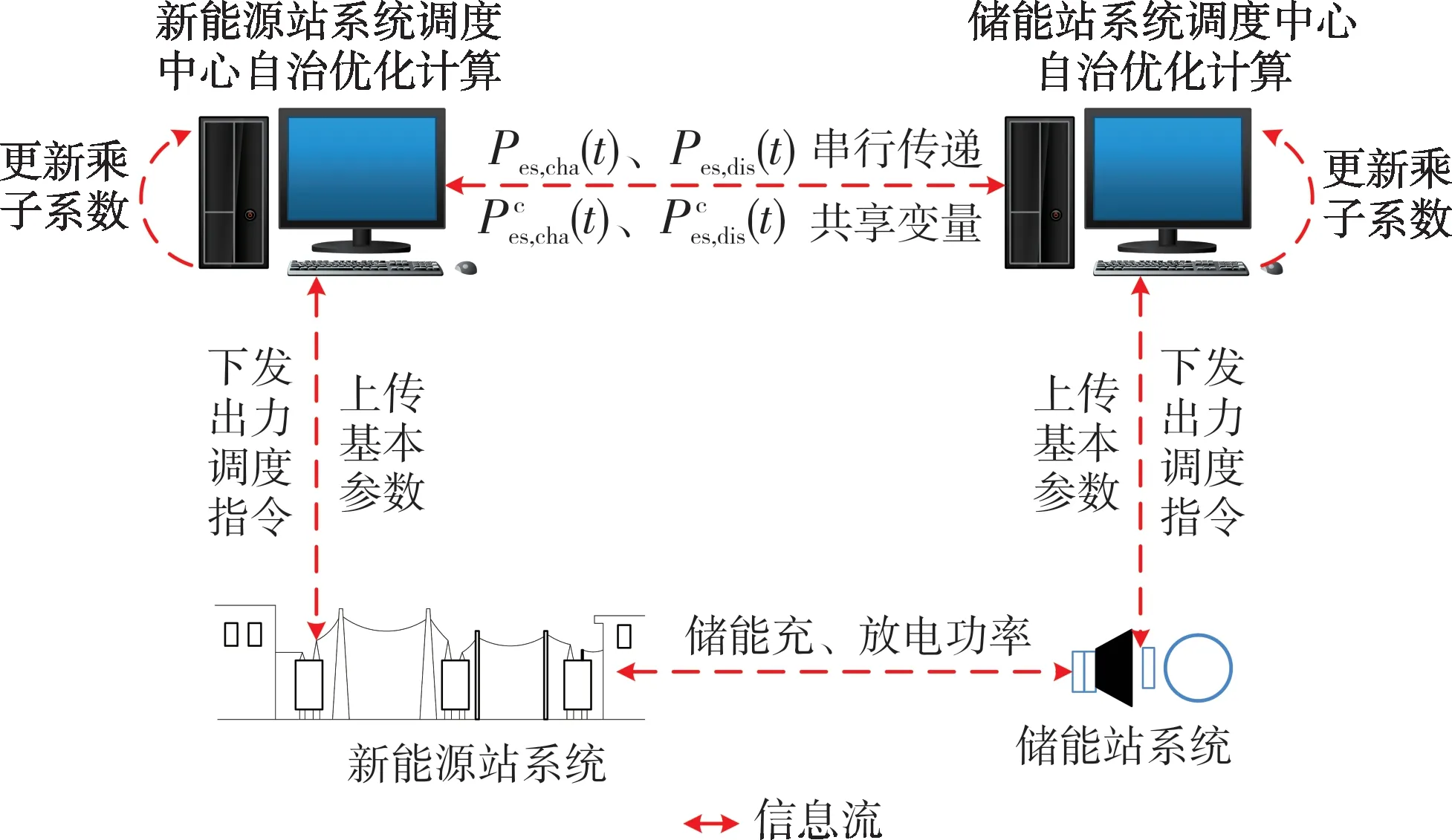
图1 新能源场站与储能电站分布式协同优化框架

新能源场站的目标是制定最优储能调度策略，在参与电网优化运行的同时尽可能消纳本地新能源，而储能电站的目标为最小化充、放电成本，因此可选择新能源场站与储能电站的共有变量——储能的充、放电功率，作为双方的协同共享变量。在新能源场站子问题中引入储能的充、放电功率，并满足以下关系：

2.2 ADMM

ADMM具有收敛性好、鲁棒性强的特点，适用于求解分布式优化问题。ADMM将大的全局性问题分解为若干个容易求解局部子问题，并通过各个子问题的协调优化得到全局问题的解。具体描述为：

式中：f(x)和g(z)为两个子问题的目标函数；x和z为两个子问题的决策变量；xc和zc为共享变量；A、B、C为耦合约束系数矩阵。式（17）耦合两个子问题。

ADMM将式（17）加入目标函数中，构造如下增广拉格朗日函数：

式中：y为拉格朗日乘子系数列向量；ρ为惩罚因子。

式（18）将两个子问题耦合变量的约束关系转移至目标函数中，是子问题的分布式求解的关键。

本文在利用ADMM求解过程中，同一时刻仅有一个子问题处于计算过程，等待求解结束将共享变量传递至另一个子问题，并处于等待过程中，待另一个子问题计算结束传回共享变量。具体迭代过程如式（19）所示。一轮求解计算完成后，按照式（20）更新拉格朗日乘子系数，并进入下一轮计算。

式中：上标（k）表示第k次迭代，下同。

2.3 新能源场站与储能电站分布式协同优化算法

基于ADMM将新能源场站与储能电站集中式优化问题分解为新能源场站子问题与储能电站子问题，如图2 所示。以各自运营成本最小化为目标，两个子问题之间通过少量多次的信息交换，实现新能源场站与储能电站的协同优化。

图2 集中式优化与分布式优化关系

2.3.1 新能源场站优化子问题

新能源场站优化子问题的优化目标为弃风成本、弃光成本和机组出力成本最小化，决策变量为电网侧发电机组出力和储能充、放电功率需求量。

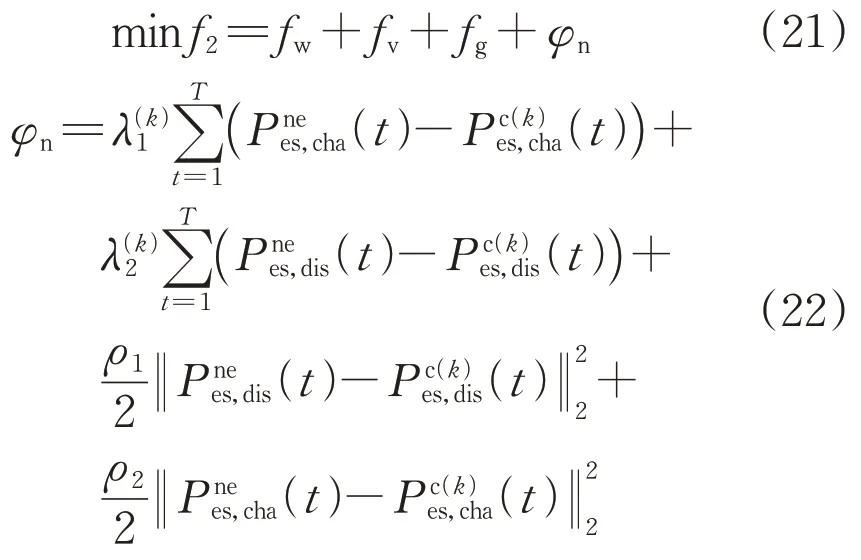
式中：f2为新能源场站总成本；和分别为新能源场站的储能充电功率和放电功率需求量；和分别为储能电站子问题第k次迭代后得到的储能充电功率和放电功率供应量；ρ1和ρ2为惩罚因子；λ1和λ2为拉格朗日乘子系数；φn为惩罚项。

约束条件与集中式优化模型中相同。此时，新能源场站子问题可以表示为：

2.3.2 储能电站优化子问题

储能电站优化子问题的目标为储能的充、放电运行成本最小化，决策变量为储能充、放电功率供应量。

式中：f3为储能电站总成本；和分别为新能源场站子问题第k+1 次迭代后得到的储能充电功率和放电功率需求量；和分别为t时段储能充电功率和放电功率供应量；φm为惩罚项。

约束条件与集中式优化模型中相同。此时，储能子问题可以表示为：

2.3.3 ADMM收敛判据

ADMM收敛判据为：

式中：ε为原始残差容忍上限。

2.3.4 算法流程

基于ADMM的新能源场站与储能分布式协同优化算法的具体求解步骤如下：

步骤1：初始化。将迭代次数k赋值为1，给定原始残差ε、惩罚因子ρ1和ρ2，设置储能站充电和放电功率初始值和拉格朗日乘子系数初始值和

步骤2：按照顺序依次计算新能源场站子问题（式（23））和储能电站子问题（式（26））。此过程中，新能源场站子问题的储能充、放电功率需求量求解结果和储能电站子问题的储能充、放电功率供应量求解结果顺次迭代，并按照式（28）和（29）更新拉格朗日乘子系数λ1和λ2。

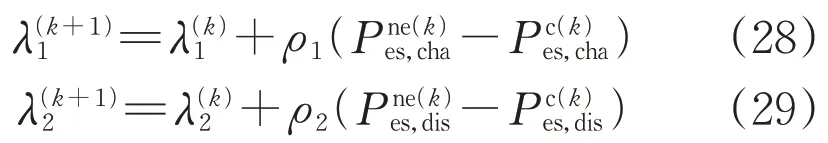
步骤3：根据式（27）判断收敛性，若收敛判据成立则停止计算并输出计算结果；否则令k=k+1，转至步骤2 进行下一轮迭代优化计算，直至收敛为止。

3 算例分析

为了验证本文所提算法的有效性，在Windows 10系统（2.50 GHz、16 GB）上利用MATLAB 编写ADMM 程序与集中式优化调度程序，调用YALMIP 工具箱和GUROBI 商业求解器进行求解。以华北地区某小型电网为研究对象，选取冬季典型日场景进行仿真分析，该电网网络拓扑如图3 所示。图3 中：1—33 为节点编号；PW1 和PW2为风电场站；PV1和PV2为光伏电站。

图3 电网拓扑结构

本文中运行调度以全天24 h 为1 个周期，1 h为1 个时段。风电、光伏以及负荷数据如图4 所示，储能参数见表1，机组参数及运维单价成本来自文献［18］。

图4 冬季典型日风、光出力及负荷曲线

表1 储能参数

3.1 分布式协同优化结果分析

图5为一个调度周期内为促进风光的消纳，储能的充、放电功率控制结果。可以看出：在1—3时段，由于风电出力较多，负荷不能完全消纳，因此通过控制储能充电可以存储多余的风电；在7—9时段，由于光伏电站开始发电，为促进光伏的消纳，储能也开始进行充电；在11—12 时段，由于是用户用电的高峰期，风光出力不足，储能开始进行放电以弥补发电缺额；在18—21 时段，由于此时光伏和风电出力严重缺额，并且处于用户负荷的高峰期，储能也开始进行放电以弥补发电不足，但是储能出力受限，弥补后仍存在的发电缺额由发电机组提供。

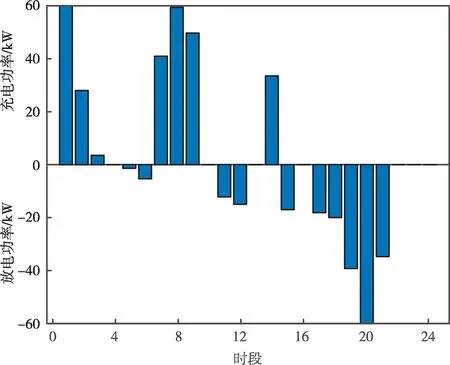
图5 储能充、放电功率控制结果

基于ADMM，通过控制储能充、放电功率实现新能源场站与储能电站分布式协同优化调度结果如图6所示。由图6的调度结果可以看出，通过控制储能的充、放电功率，在负荷低谷时期利用储能进行充电，在负荷高峰时期利用储能进行放电，可以有效促进风电以及光伏的消纳，实现系统的经济运行。

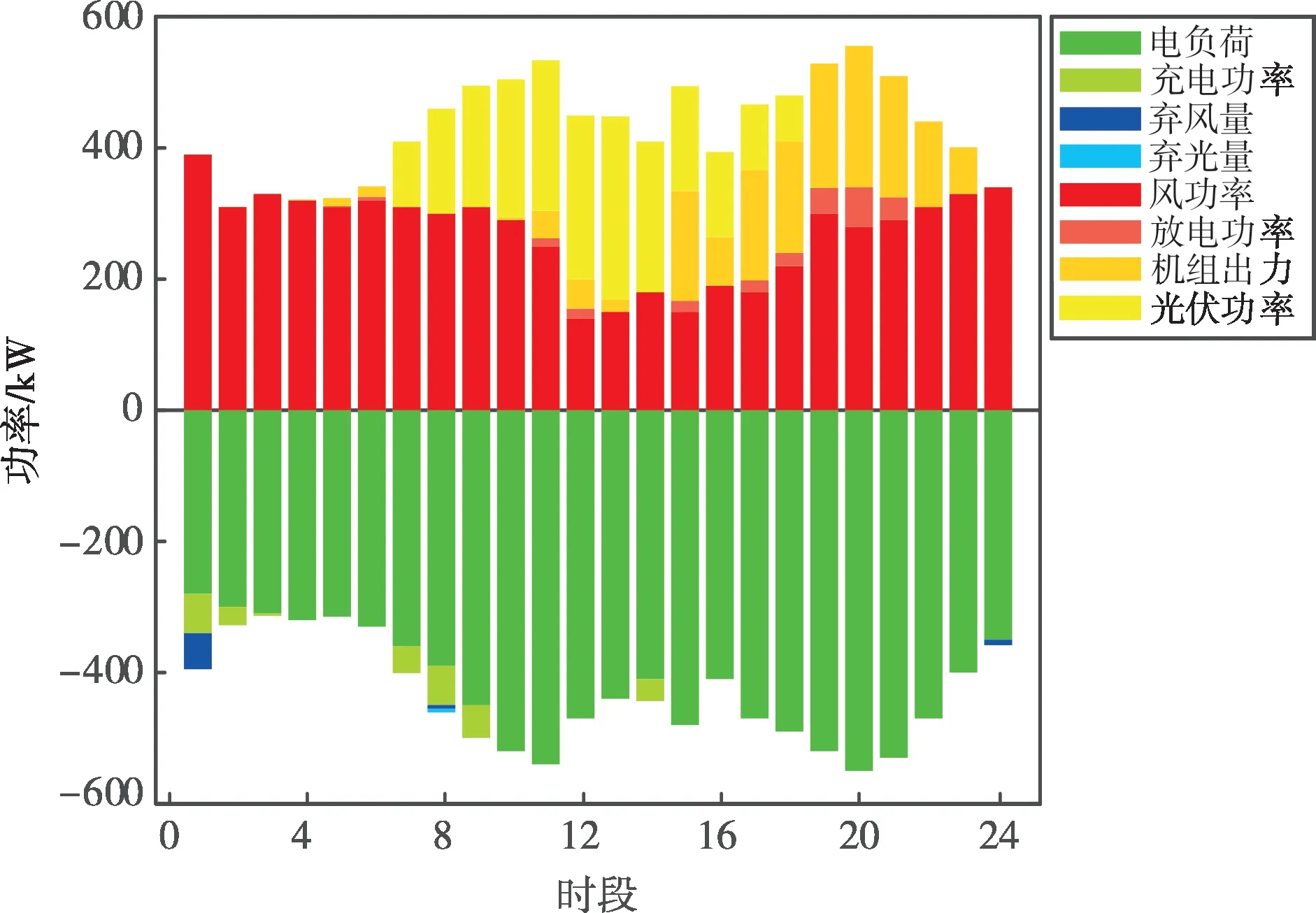
图6 分布式调度结果

未经优化调度与经过分布式协同优化调度的弃光、弃风功率对比如图7 和图8 所示。可以看出，经过优化调度后，弃风、弃光功率明显下降，验证了本文算法对促进新能源消纳的有效性。

图7 未经优化调度与分布式协同优化调度的弃光功率对比

图8 未经优化调度与分布式协同优化调度的弃风功率对比

3.2 集中式算法与分布式算法对比

采用集中式优化方法和基于ADMM的分布式优化方法所得到的计算结果见表2。

由表2 可以看出，基于ADMM 的新能源场站与储能电站分布式协同优化方法可以获得与集中式优化方法相同的调度方案，两者的储能侧成本与新能源侧成本基本一致，验证了本文模型及所提方法的有效性和正确性。

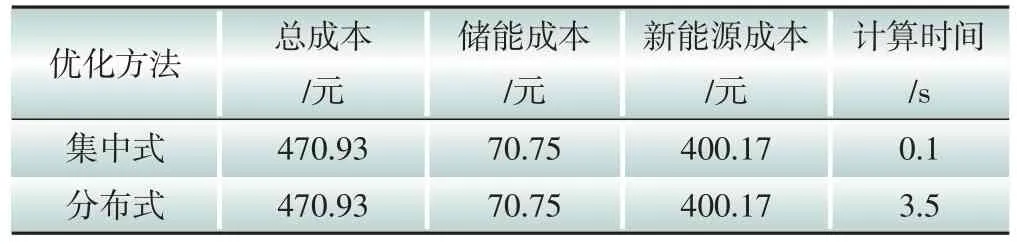
表2 运行费用和计算时间

集中式优化方法不需要进行迭代计算，因此计算时间较短，但集中式优化调度方法不适用于当前电力系统的分散自治决策环境。本文将新能源场站与储能电站分开考虑，一方面适用于当前新能源场站和储能电站分属于不同利益主体的情况，另一方面避免了集中式优化算法数据量大、模型复杂及求解困难等问题，能够有效实现储能电站与新能源场站的分布自治决策和协同优化。

集中式优化调度与基于ADMM的分布式优化协同调度的弃风、弃光功率对比如图9 和图10 所示。可以看出，两种方法都可以实现新能源的消纳，有效降低电网的弃风量和弃光量，提高电网运行的经济性。两种调度方法对弃风和弃光功率的求解结果相同，进一步证明了本文方法的有效性。

图9 集中式优化调度与分布式协同优化调度的弃风功率对比

图10 集中式优化调度与分布式协同优化调度的弃光功率对比

基于ADMM的优化方法计算过程中，残差收敛曲线如图11 所示。可以看出该模式具有极快的收敛性，能在短时间内求得与集中式优化方法相同的解。在迭代初期给定储能站的和初始值为0，因此残差值较高。随着迭代的进行，储能侧的充、放电功率向新能源侧的值逼近，残差值逐渐减小，直到趋近于0。在本算例下，共享变量更新速度快，可以很快达到收敛。

图11 残差收敛曲线

4 结语

本文针对新能源场站与储能电站的多主体分布自治决策的特点，提出了一种基于ADMM的新能源场站与储能电站分布式协同优化方法，通过与集中式优化调度方法的对比分析，得出其具有以下的特点：

1）面向新能源场站与储能电站的多主体决策特点，避免了集中式优化调度方法中数据繁多、求解困难的弊端，使调度过程更加符合新能源场站与储能电站由不同利益主体分开决策的特点。

2）具有很好的收敛性，可以在短时间内求得与集中式优化调度方法相同的控制策略。