基于广义极值分布的东昆仑山断裂带周边区域地震危险性分析
赵宜宾,王福昌,任晴晴,张艳芳,钱小仕
(防灾科技学院,河北三河 065201)
0 引言
青藏高原是我国地质活动最为活跃的地区,由于各块体之间强烈的相互作用,使其成为研究大地动力学的良好实验场,也为学者探索地壳构造与形变过程[1]提供了良好的环境。东昆仑断裂带是青藏高原北部秦祁昆块体与可可西里-巴颜喀拉块体的边界断裂带,是印度板块向欧亚板块俯冲过程中沿东昆仑古构造缝合线复合的一条岩石圈断裂[2],断裂带东北部主要是柴达木块体,西南部主要是巴颜喀拉地块的中部,东昆仑山断裂带是两块体的分界地带,该断裂带及周边地区发生地震次数多,强度大。自1900年以来,MS7以上的强震发生过7次,特别是2001年昆仑山口西的MS8.1巨震,引发了一系列周边区域物理场的变化,相关特异性信号对于研究周边地质活动和地震预测有重要的研究价值,地震地质研究人员分别从地震前兆、破裂过程、余震序列特征和应力影响[3-6],以及震前信号特征分析[7-9]和地震断层的分析[10-12]等不同角度,对这一区域地震发生情况进行了深入的研究,并取得了一些有益的成果。
运用统计分析方法从历史数据挖掘信息,寻找地震发生规律,对于减少地震灾害损失有着重要意义。作为以极端风险事件为研究对象的极值理论,已经被证实其在灾害预测[13]、风险评估[14-15]等领域有着良好的应用前景。极值理论是被Nordquist[16]最先引入到地震预测中的,陈培善等[17-18]对于地震预测极值模型的构建从理论上做了有益的探索,陈虹等[19-20]对极值模型在区域地震危险性评价中的应用做了深入探讨。钱小仕[21-22]梳理了地震危险性评价指标,并利用广义极值分析方法对强震分布的特征进行了研究。
以文献[21]研究为基础,利用几何分布相邻两次超阈值时间长度相等的特征,重新定义了地震重现期和重现最大震级,并以此为基础,给出了用于地震危险性评估的多个指标及计算方法,完善了极值模型应用于地震安全评价的理论体系,并通过对东昆仑山断裂带及周边区域的地震危险性评估来证明本文所建的极值模型的有效性。
1 广义极值分布理论概述
极值分析理论的主要研究对象是在特殊情况下发生极端风险事件,是风险管理和安全评价的重要建模工具,本文以文献[23]的极值统计分析的理论为主要参考,讨论地震危险性评价的极值分析模型。
1.1 广义极值分布的基本理论
极值分析是以Fisher[24]提出的最大值吸引场为基点,开展相关理论研究的:
定义1:设X1,X2,…,Xn,…是分布函数为F(x)的独立同分布随机变量序列,对于∀n∈Z+,令Mn=max(X1,X2,…,Xn),若存在常数列{an>0}和{bn}使得
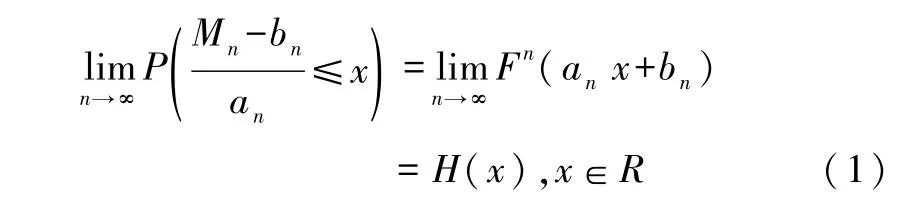
成立,则称随机变量X属于极值分布H(x)的最大值吸引场,记作X∈MDA(H)。
非退化的 H(x)可以用广义极值(Generalized Extreme Value,下文简记为GEV)分布的分布函数表示:
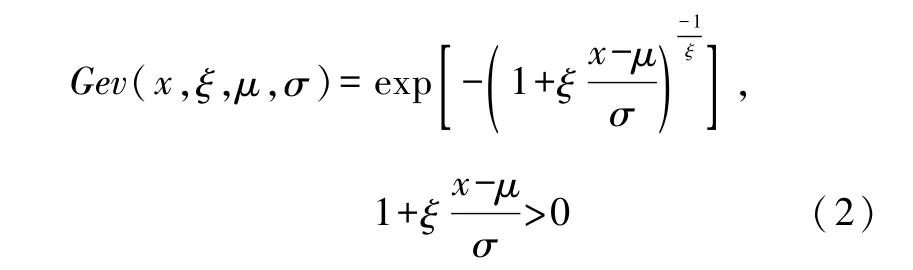
其中,μ是位置参数;σ是比例参数;ξ是形状参数。
GEV分布可分为三种类型:当ξ>0时,称其为Fr˙echet分布;当ξ=0时,称其为Gumbel分布;当ξ<0时,称其为Weibull分布,此时分布具有有限上端点。鉴于形状参数的重要性,GEV分布的分布函数记为Gevξ(x)。相应的密度函数记为gevξ(x),见式(3):
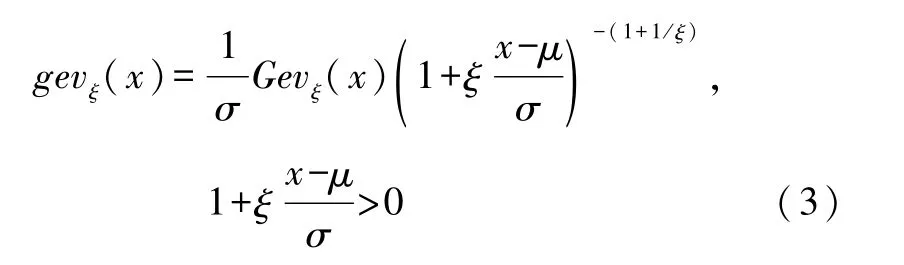
在实践应用时,对于观测数据的分布F(x)很难确定,即使能够确定F(x)类型,对F(x)满足吸引场的验证也不易实现。Frechet[25]研究表明若数据区组最大值的渐近分布存在,则其服从GEV分布,这个研究成果为极值理论用于风险评价提供了理论基础。
综上所述,GEV分布建模过程为:首先对观测数据进行区组划分(区间长度尽可能大,以满足渐近独立性条件),以各组中最大值作为研究数据;其次对模型进行参数估计;然后对模型进行适用性检验;最后应用极值模型对给定区域进行风险评估。
1.2 GEV分布的参数估计
用于地震危险性评价的极值模型主要为ξ≠0的类型,利用极大似然估计法可求得ξ≠0时GEV 分布的参数(μ,σ,ξ)的估计值为(^μ,^σ,^ξ),同时由参数估计的渐近协方差矩阵PCOV,可求得各参数置信水平为1-α的置信区间:

其中,Z1-α/2是标准正态分布的分位数。
求公式2的反函数,依极大似然估计的不变性,可得分位数xp的估计为

当ξ<0时,令式(5)中的p→1,可求得GEV分布上端点的极大似然估计为

1.3 基于统计分析的地震危险性指标
令X1,X2,…,Xn为独立同分布的等间隔震例序列,分布函数为Gevξ(x)。设首次超阈值u的时间为T1=min{k:Xk>u},令P(X>u)=1-Gevξ(x)=q,则有
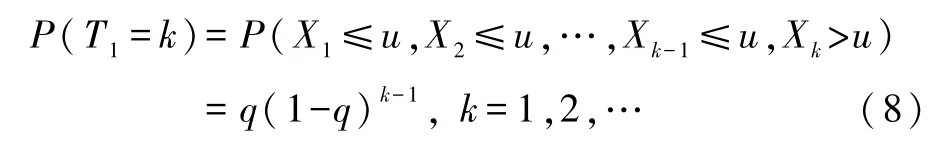
即T1服从几何分布,由几何分布性质可知,E(T1)=1/q=1/Gevξ(u)。同时还可以证明相邻两次超阈值的时间间隔与首次超阈值时间是一致的,据此定义地震重现期如下:
定义2 给定震例序列X1,X2,…,Xn,…及阈值u,若序列中相邻两次超阈值的平均时间为T(u),则称u为重现最大震级,相应T(u)称为重现期。
相应的地震危险性评价指标计算如下:
(1)重现期:给定阈值u,根据定义2可得超阈值的震级重现期为

(2)重现最大震级:给定重现期T,可得重现最大震级为
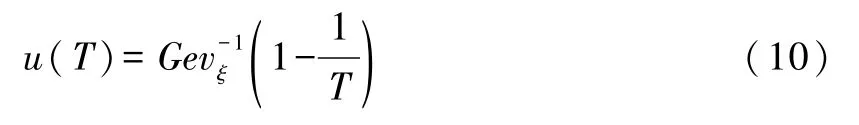
(3)重现频数:定周期L内,超阈值u的地震平均发生次数为

(4)超阈值地震危险性:令周期L内超过u的地震次数为K,则K~B(L,1-Gevξ(u)),故在周期L内,发生超阈值地震的概率为
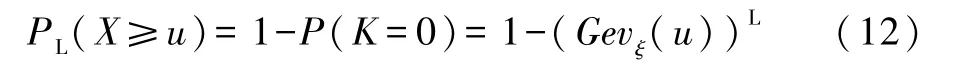
(5)最大平均震级:若X~Gevξ(u),由期望公式[21]可得定周期内最大平均震级为

2 东昆仑山断裂带及周边区域危险性分析的GEV模型构建
本文采用面波震级MS作为地震大小度量单位,利用国家地震科学数据共享中心的正式地震目录为源数据,若面波震级缺失,利用近震震级Ml与面波震级转换公式[26]:MS=1.13Ml-1.08进行数据补充,依据张国民[27]提出的大陆活动地块边界,截取东经 82.8°~104.2°,北纬33.5°~37.1°区域内的4385个震例作为东昆仑断裂带及周边区域地震危险性分析的源数据。考虑研究对数据样本的相互独立要求,采用C-S法[28]进行余震删除,得到3616个用于地震危险性评价的震例信息,震例空间分布如图1所示。
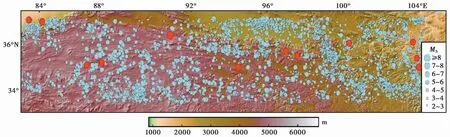
图1 地震空间分布Fig.1 Spatial distribution of ear thquakes in the study
东昆仑山断裂带及周边区域地震分布情况是呈东北频率高、震级低,西南及中部频率低、震级高的特征。研究区域地震发生频繁,MS7以上的超强震(图中红色震中标识)在研究区域的东部相对发生较多,说明这一部分地质条件不稳定。
源数据中1900年前只有25条记录,基本上是MS5以上震例,黄玮琼[29]提出该区域MS5以上震例信息从1937年开始丰富,完整的地震记录始于1970年台网建立后。1930年到2019年的MS3以上震例M-t关系如图2所示,该区域MS4以上震例信息从1950年开始丰富,完整的MS3以上震例记录始于1965年。考虑到统计分析模型所需样本在时间上的连续性,同时尽量最大程度地保留研究区域的地震特征。本文以半年为间隔,截取1950年以后的区间震级最大值为地震危险性分析的研究样本。
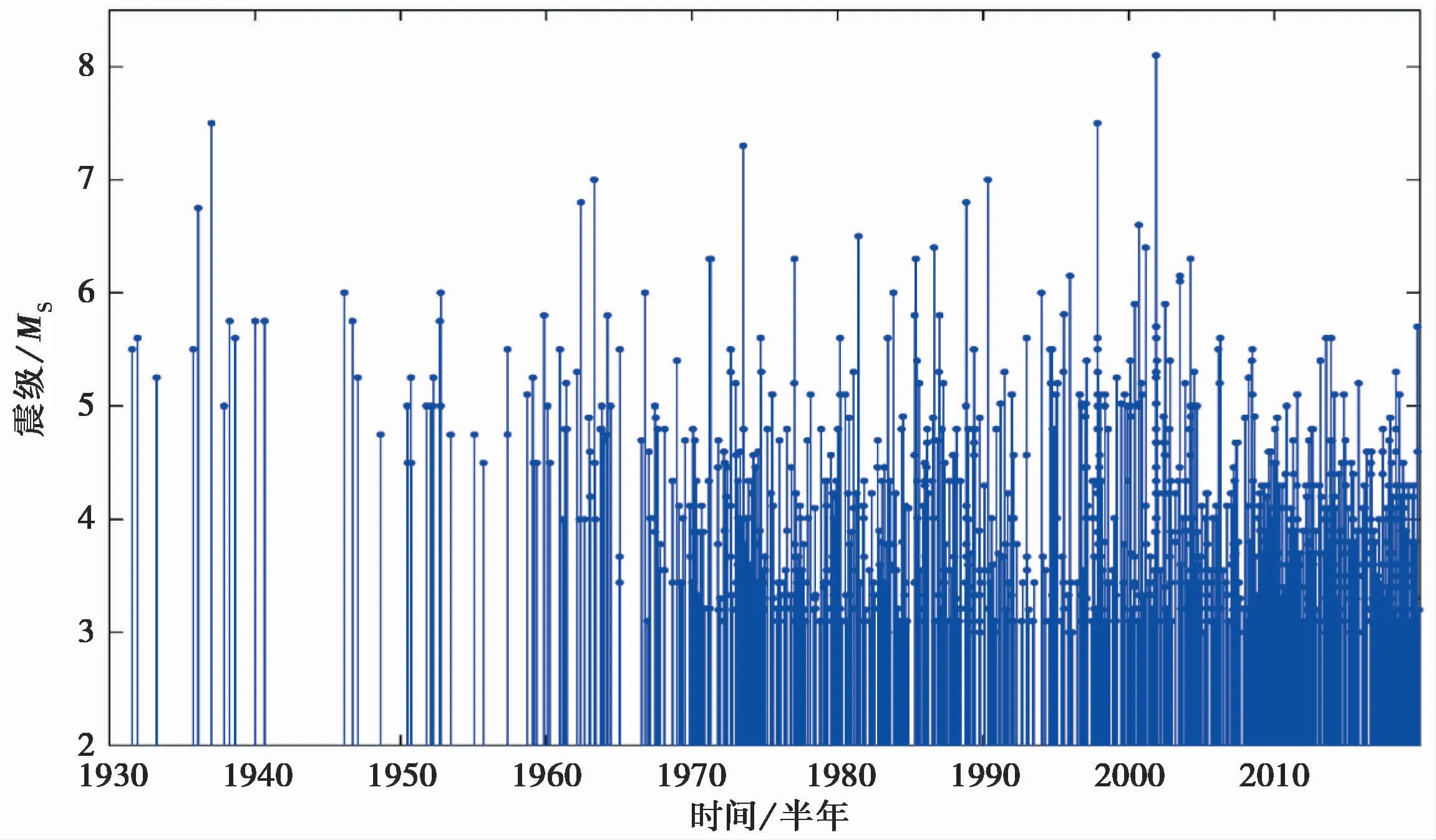
图2 震级-时间图Fig.2 Magnitude-time diagram
根据前文的GEV 分布参数估计方法,以matlab软件为计算平台,通过数值计算求得GEV分布主要参数的极大似然估计值及95%的置信区间(表1)和协方差矩阵Pcov(公式14)。

GEV模型的形状参数^ξ<0(表1),且置信区间的上限小于0,表明研究区域半年最大震级分布服从Ⅲ型极值分布,有理论震级上限。

表1 GEV分布参数极大似然估计Tab.1 Maximum likelihood estimation of GEV distr ibution parameters
GEV模型对于东昆仑地震带及周边区域危险性评价的适用性诊断图如图3所示。估计的密度曲线和直方图轮廓趋势基本吻合。震级大于MS3的样本几乎全部落在重现最大震级为95%的置信区间内,结合^ξ<0,表明重现最大震级渐近趋于定值,P-P图和Q-Q图的散点沿45°直线小幅波动,说明理论分位与观测值分位数几乎一致。对比Gumbel[14-15]危险性评价模型(适用性检验如图4所示),当震级超过MS5.5时,Gumbel模型预测值与观测值开始明显偏离,故本文所构建的GEV模型更适合做研究区域的地震危险性评价模型。

图3 东昆仑断裂带周边区域半年最大震级数据GEV拟合诊断图Fig.3 GEV model fitting diagnosis chart of semi-annual maximum magnitude data in the surrounding area of east Kunlun Mountain fault
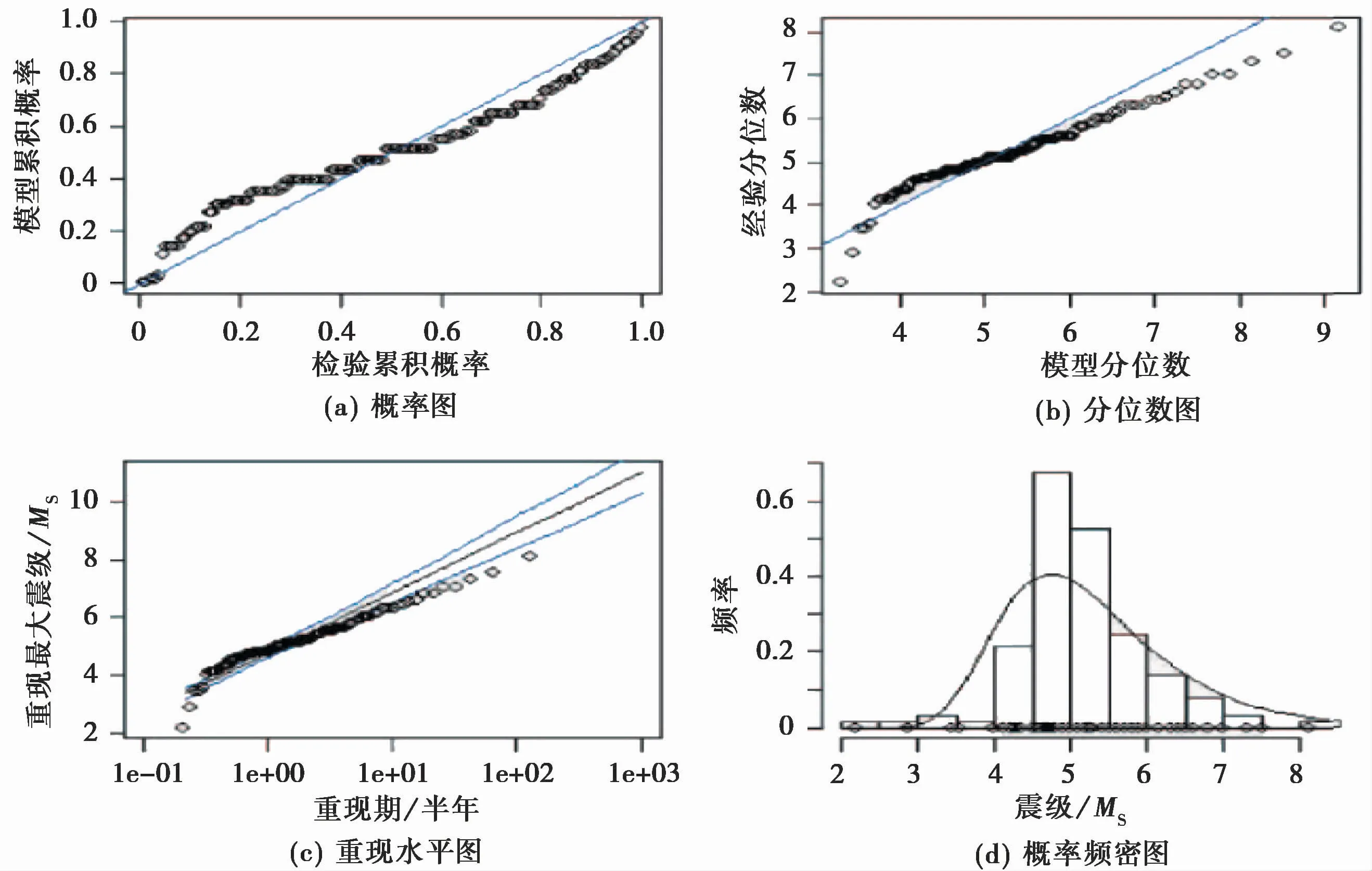
图4 东昆仑断裂带周边区域半年最大震级数据Gumbel模型拟合诊断图Fig.4 Gumbel model fitting diagnosis chart of semi-annual maximum magnitude data in the surrounding area of east Kunlun Mountain fault
利用公式12计算70年来超阈值发震频数,与样本信息对比(表2),可得随着阈值的增加,超阈值理论发震次数和实际情况基本一致。

表2 70年超阈值理论与实际发震频数对比Tab.2 Comparison between theoretical ear thquake fr equency over threshold and actual earthquake frequency in past 70 years
综上所述,本文所构建的GEV模型能够比较客观地反映研究地区的地震活动规律,因此用此模型对东昆仑山断裂带及其周边区域所做的地震危险性分析是客观可信的。
3 东昆仑地震的危险性分析
依据构建的GEV模型,对东昆仑山断裂带及周边区域的地震危险性分析如下:
(1)地震危险性宏观分析
根据公式15计算得,东昆仑断裂带及周边区域半年期最大震级的均值为MS5.2,属于中强震水平,说明该区域发生中强震的危险性极高。通过公式8可得,该区域的最高理论震级为MS8.98,表明东昆仑山断裂带及周边区域存在发生超巨震的可能性。
(2)发震可能性分析
东昆仑山断裂带及周边区域部分震级的复发周期预测如表3所示,震级-复发周期图(图5)显示研究区域MS5.5以下地震发生相当频繁,超过MS6地震的复发周期呈指数增长。表3数据表明,研究区域MS5左右的中强地震几乎每年都要发生,MS6.5左右的强震大约6年发生一次。
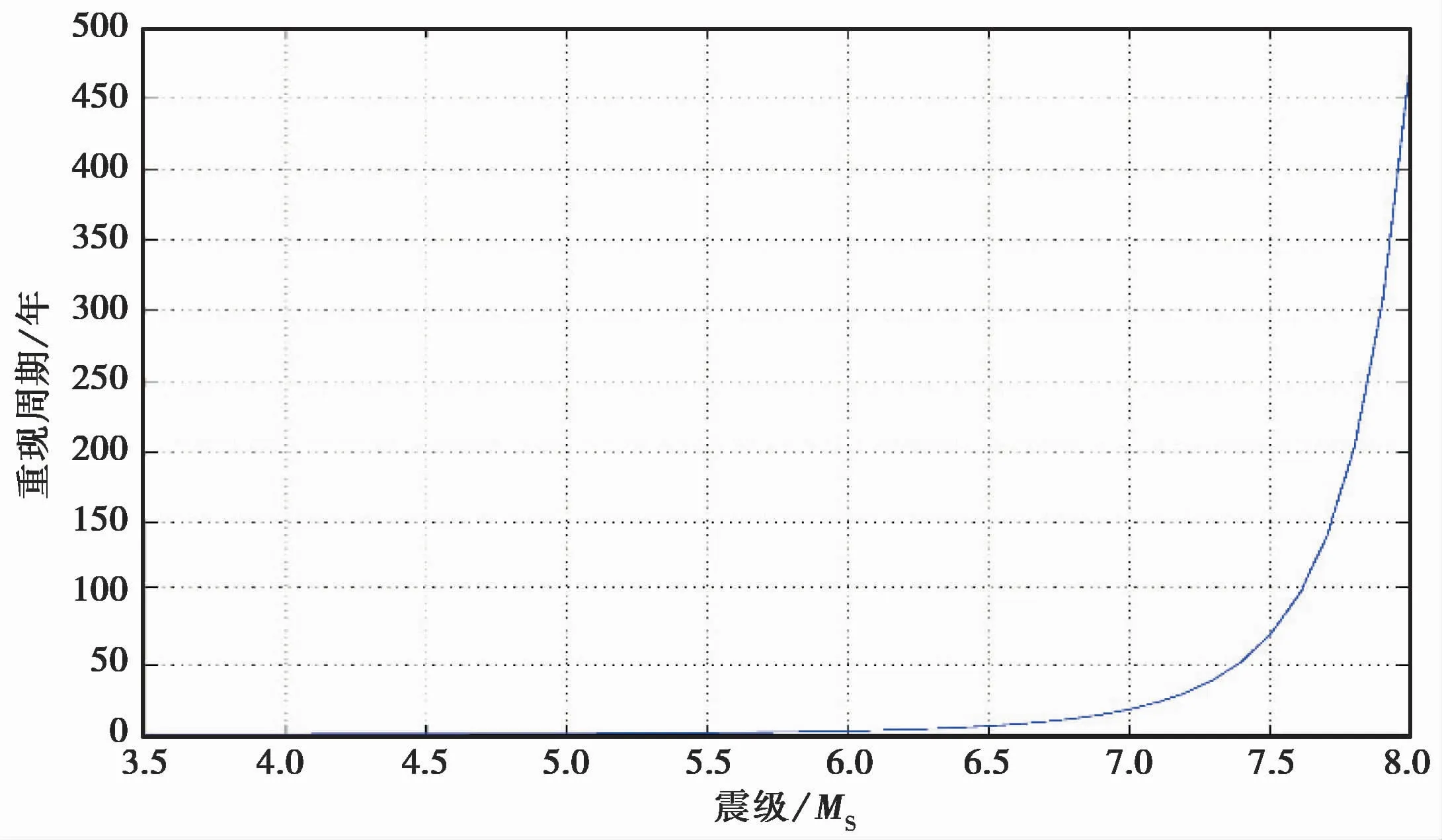
图5 震级与复发周期趋势关系Fig.5 Relationship between magnitude and r ecurrence period

表3 各震级理论复发周期(年)Tab.3 Theor etical recurrence per iod of ear thquakes in different magnitude(a)
东昆仑断裂带及周边区域在50年周期内发生超MS7地震的可能性为94%,超MS7.5的地震可能性为51%,而在100年内发生超MS7.5地震的概率则提升到76%,以上数据说明研究区域的孕育地震的能量聚集比较快,地质活动比较频繁。
(3)重现最大震级分析
东昆仑断裂带及周边区域定周期的重现最大震级水平和95%的置信区间如表4所示。在理论上,东昆仑断裂带及周边区域10年一遇的地震约MS6.7,重现最大震级在MS7~MS7.6的地震重现期的跨度为18~100年,说明该地区百年一遇的地震应该为MS7以上,结合100年重现最大震级的95%置信上限为MS8.0,表明在该地区在100年重现期内存在发生超强震的可能,以上结论从另一角度表明该地区孕育地震的能量聚集迅速,断层之间相互作用是相当强烈的。研究区域分别在1997年和2001年在中西部发生过两次超MS7.5的超强震,1963年和1990年在东部发生过两次MS7地震,从地震能量释放和发震周期来预测,未来一段时间,研究区域的东部存在发生MS7左右地震的可能性很高。

表4 定周期内的重现最大震级及置信区间Tab.4 Maximum r ecurrence magnitude of earthquakes and its confidence interval in different recurr ence period
4 总结与展望
本文对GEV分布模型的构建过程做了系统的阐述,重新定义了地震重现期和重现最大震级,给出了完整的地震危险性评价指标。利用所建GEV模型从多个角度对东昆仑山断裂带及周边区域的地震危险性做较为全面的评估,所得结论可作为研究区域地震安全性评价的重要参考信息。
虽然GEV模型能够对地震危险性做出相对客观的评价,但由于模型构建过程所用的是区组最值信息,最值信息只能表述研究区域在特定时间段的极端情况,并不能全面反映研究区域的地震活动规律。如何从更充分地利用数据信息角度来优化GEV模型的构建过程将是作者后续主要的研究方向,以使构建的地震安全评价系统更加合理和有效。

