基于时空图小波神经网络的手部动作识别方法*
刘电霆,梁桂宾,周运刚
(1. 桂林理工大学机械与控制工程学院,广西 桂林541004;2. 桂林理工大学南宁分院,广西 南宁530000;3. 广西科技大学机械与交通工程学院,广西柳州545000)
引 言
众所周知,相对于传统的视频监控方式,利用计算机视觉技术实施监控,大大提高了系统的自动化、智能化程度。同时,随着计算机视觉的发展,识别人体动作的准确性和复杂性也在不断提高。尤其是近几年来,由于骨架精确位姿估计方法的成熟[1],利用骨架序列对人体行为进行识别是目前研究的热点。在制造领域,工人手部动作的识别对判断工人操作、监控异常行为、事故预警等都具有重要意义。
近年来,国内外研究者们对人体动作、姿态识别问题进行了一系列科学研究,研究方法主要包括人工特征方法和深度学习方法[2]。人工特征方法是指人工设计特征以实现动作识别,首先是根据骨架序列的特点在个人认知的基础上设计出该序列特征,然后利用这些特征表征视频内连续的人体动作。一般来说,这些人工特征都具有明确的物理意义,如关节轨迹的链码、关节位置坐标等。例如,文献[3]提出一种SoCJ描述子来描述手势特征,是将手关节坐标序列展开成特征矩阵,并利用LibSVM软件包进行识别分类,在DHG数据集上取得了良好的识别效果。文献[4]提出基于李群的骨架特征描述,通过将关节点转换到李代数的向量空间实现手势的分类,在MSR-Action3D、UTKinect-Action和Florence3D-Action三个数据集上取得了良好的识别效果。但人为设计的特征可能会因为人的主观臆想而忽略数据的客观联系,并且一般依赖于数据,即面向特定识别任务。深度学习方法采用大量数据拟合的模型,避免了人工设计特征的要求,且具有一定程度的泛化能力,可以更好地表示动作,因此能够有效地自主学习和识别动作。比如,文献[5]提出了一种局部感知长短期记忆(Long Short Term Memory, LSTM)网络,可以用来构建人体各部位特征的长期时间相关性模型。实验结果显示,局部感知LSTM网络在RGB+D数据集上的识别率高于其他人工特征识别方法。
针对工人手部动作的检测和识别方法,本文提出了一种时空图小波神经网络(Spatio-Temporal Graph Wavelet Neural Network, ST-GWNN)算法。本文主要聚焦于工人使用工具时的手部动作,以手部骨架构建拓扑图,从而对手部动作进行检测和识别,取得了良好的识别效果。
1 相关工作
时空图卷积神经网络(Spatial Temporal Graph Convolutional Network, ST-GCN)是将图卷积神经网络(Graph Convolutional Network, GCNN)运用到基于骨架的动作识别中的方法,是利用图卷积将骨架序列映射到特征空间,以及利用时间卷积来学习关节轨迹信息,使得模型能够表示各个类别的概率解。比如,文献[6]将骨架视为关节拓扑图,并运用图卷积建立模型。由于图卷积能够准确融合相邻关节的坐标信息,因此能够有效地将关节的空间信息映射到特征空间。骨架特征十分依赖空间位姿信息,当相机伴随采集对象大量运动时(如Kinetics数据集),帧与帧之间关节的相对位置会存在一定程度的失真,使得识别效果下降。文献[7]提出了手势图卷积神经网络,将图卷积应用于手势识别,在DHG-14/28数据集和SHREC’17数据集上均具备了不错的辨识能力,并且辨识迅速,因此这种手势图卷积神经网络(Hand Gesture - Graph Convolutional Network, HG-GCN)技术可以应用到实时场景。但相较于时空注意-残差-时间卷积神经网络(Spatial Temporal Attention- Residual - Temporal Convolutional Network, STARes-TCN)[8],HG-GCN的学习能力较弱,需要更多的数据才能达到较好的识别效果。文献[9]提出了一种双流自适应图卷积神经网络(Two-stream Adaptive Graph Convolutional Network, 2s-AGCN)算法,同时利用一阶邻接节点和二阶邻接节点组成双流神经网络,克服了ST-GCN对骨架拓扑图序列分类缺乏柔性的问题,同时也面临着空间位姿依赖问题,对非固定设备录制场景,识别效果不是十分理想。文献[10]提出了结构诱导型图卷积(Structure-induced Graph Convolutional Network, Si-GCN)算法,考虑到身体不同部位之间存在接触连接,将骨架图分成部位的内连接和外连接,使得Si-GCN能够更准确地连接骨架图的邻点,从而更有效地聚合关节点的运动信息。与传统的卷积类似,Si-GCN在融合高阶的邻接节点信息时,会引入更多的噪声,使得识别性能下降。另一方面,为了解决将整个骨架序列作为输入时前馈网络不能有效提取动作间语义信息的问题,文献[11]提出了反馈图卷积神经网络(Feedback Graph Convolutional Network, FGCN)算法,将动作序列分成若干段依次输入模型,而每一阶段的图卷积结果会反馈给下一阶段的图卷积层,这使得图卷积层能够提取并融合每段动作序列的高层语义信息,但每一阶段需要进行一次全连接层运算,大大增加了计算成本。
最近,图卷积成为了深度学习领域的研究热点。卷积运算作为文本、图像等网格化数据处理的基本方法,在深度神经网络中验证了其可行性,但是卷积运算无法直接在非网格化的无向图中使用。为了能够在无向图上实现卷积运算,文献[12]提出以图结构的拉普拉斯矩阵取代卷积运算,并据此完成了非网格化数据的图卷积处理,但模型参数通常更加复杂。为了降低图卷积的模型参数复杂度,文献[13]用切比雪夫多项式逼近图卷积核,在保持卷积局部性的同时,可以大大减少参数量。在此基础上,文献[14]给出了一个有效的构造更简单的图卷积,但其模型参数过于简洁,导致分配到一阶邻域上的权重相同,这削弱了模型对空间相关性信息的敏感度。文献[15]将经典的递归神经网络推广到图卷积中,以实现对图序列进行建模,但容易出现过拟合现象,需要对数据进行正则化处理。
在图小波方面,文献[16]为了提升小波变换的效率,提出一条能够简化构造图小波的思路,但是需要对构造的小波是否形成Riesz基进行验证。文献[17]为了避免进行拉普拉斯特征分解,提出使用切比雪夫多项式逼近小波基,从而降低计算复杂度。文献[18]利用图小波编码的局部信息和尺度相关信息,在不同尺度上识别群落结构,但对谱图各分支的估计需要大量运算成本。为了描述图卷积的局部特性,文献[19]利用小波变换取代傅里叶基的图卷积,使得邻点权重分配具有极高的柔性,但卷积核上的参数复杂度与节点数成正比。为了解决这个缺点,本文在图小波的基础上,对卷积核进行改进,提出了一阶图小波卷积,保留了超参数对邻域范围的调整特性,减小图卷积的参数复杂度,并将其应用于行为识别的问题上。
2 模型构建
本文以人手动作识别为主,论述动作识别的模型建立方法。将人手骨架定义为关节拓扑图,从而建立手关节动态时间序列。直观上,手关节由手骨连接在一起,手骨可表示为关节拓扑图的连接边,手关节的空间姿态可表示为无向图输入信号,如图1所示。在手骨图Gt= (Vt,ε,A)中,Vt表示t时刻手骨拓扑图的关节集合;ε表示关节顶点连接边的集合;A ∈Rn×n表示手骨图的邻接矩阵,n表示图谱的节点个数。
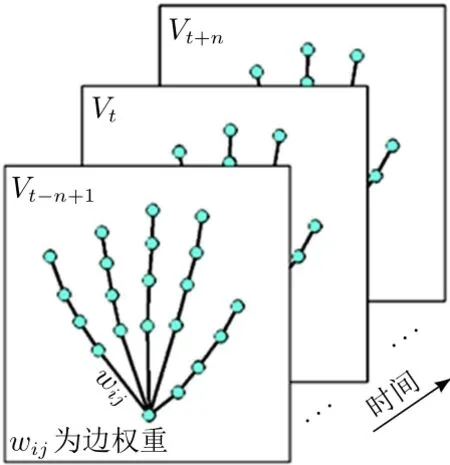
图1 手部骨架拓扑图
2.1 图小波卷积提取手部骨架特征
从数学角度来看,手关节和关节间连接的手骨构成了一种天然的无向图。本文将手关节信息通过图小波卷积映射到特征空间,从而实现手部动作的识别。
图小波卷积采用小波作为基底,相比于采用傅里叶基的图卷积,小波基可以使用切比雪夫多项式近似得到,因此拥有更高的变换效率[17]。由于图小波基随着邻域扩散,其权值逐渐衰减,所以小波基通常拥有更高的稀疏性。图小波具有局部特性,即以每个节点为中心进行卷积操作时,中心节点只与邻域内的节点进行特征融合[19]。图小波的邻域范围与超参数s有关,这使得图小波更加灵活。图小波基的变换公式[19]如下:

式中:U是拉普拉斯特征矩阵;Gs= diag(esλ1,··· ,

式中,卷积核F=diag(θ),θ ∈Rn,小波系数向量θ为模型训练参数。虽然卷积的运算时间不变,但图卷积的参数复杂度从O(n×p×q)减小到O(n+p×q)。
2.2 快速近似图小波卷积
在式(4)中,图小波的卷积核F=diag(θ),θ ∈Rn仍存在参数复杂度为O(n)的限制,其参数个数与节点数成正比。对卷积核进行非参数化改进,图小波的卷积核F可以定义为:


2.3 图小波卷积的一阶近似

2.4 图神经网络框架
本文模型主要以ST-GCN框架为基础,主要由时空图小波(ST-GWNN)组成。其中,空间卷积由一阶图小波卷积组成,时间卷积为9×1的一维卷积。STGWNN图卷积块由空间卷积和时间卷积垂直堆栈而成,如图2(b)所示。整体模型框架由10个ST-GWNN块垂直堆栈而成。为减小梯度消失的影响,在每个ST-GWNN块间引入残差机制,具体如图2(a)所示。
图2(a)表示ST-GWNN的框架。将关节特征输入ST-GWNN,最后输出到SoftMax层,得到各种动作

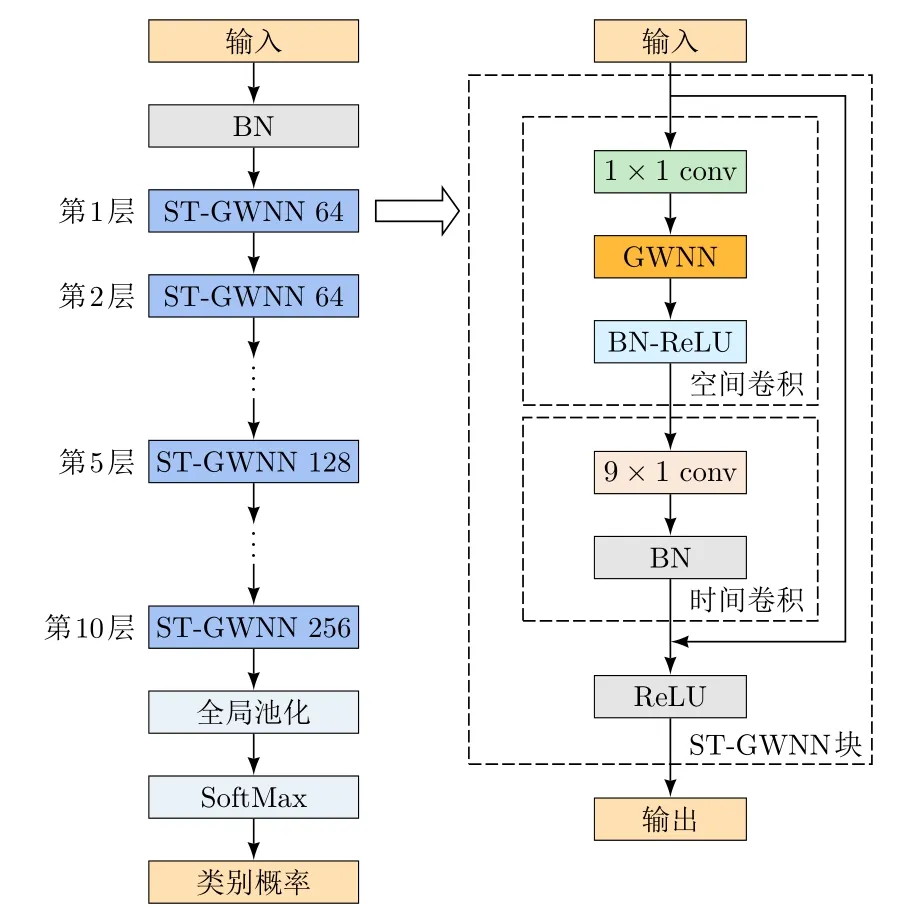
图2 图神经网络框架
3 实验测试
通过实验对ST-GWNN的识别有效性进行检验。设定4种使用工具(游标卡尺、六角扳手、大锤和螺丝刀)的手部动作,并且设定玩智能手机时的动作来模拟厂房内工人的违规施工情况。每种动作有约50个样本,并按照2:8的比率随机抽取选出实验集和训练集。动作视频片段如图3所示。实验还对前沿的识别算法进行了对比,并分析超参数s对识别性能的影响。

图3 机械数据集各动作手骨架采样的视频片段
3.1 实验搭建
实验的软件环境是Ubuntu 16.04操作系统和Tensorflow 2.1,计算机CPU为Intel Core i5-9600KF,显卡为Nvidia RTX 2080 super。
本文用到的数据集是无手骨骼数据的原始录像,车间里采集到的视频同样是不包含关节数据的图像,所以必须对数据集做预处理以提取关节数据。首先通过开源库openpose[1]提取出手关节数据。每个动作序列的最大帧数为300帧,则各个录像在获取骨架的关节位置(x,y)后,形成一组(2,300,21)张量,其中21对应手关节个数。实验中,如果一组数据不足300帧,则采用填补零(padding)的方法来满足最大帧数要求。将经过预处理的数据集分别放到ST-GCN和ST-GWNN中进行训练,实验结果如表1所示。由2.3节可知,GWNN的主要参数是超参数s,表示图卷积的作用域,即图卷积的局部性。实验中依次调整超参数s,观察其对识别效果的影响。
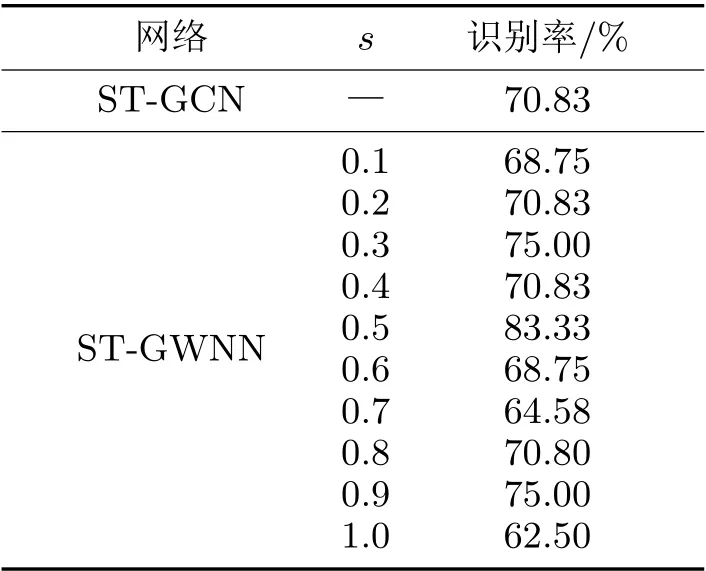
表1 ST-GCN和ST-GWNN的对比
3.2 分析与讨论
从表1数据可知,在超参数s测试的范围内,STGWNN的识别率最高可以达到83.33%,显著高于STGCN。但是当s= 0.1时,ST-GWNN的识别率仅为68.75%,略低于ST-GCN模型。随着s逐渐增大,STGWNN的识别率明显改善。当s= 0.5时,识别率达到最大值。在s >0.5后,识别率又有所下降。由此可以直观地看出,通过在一定范围内调整s能够明显改善识别能力。
在相同的数据集和神经网络框架下,ST-GWNN和ST-GCN的动作识别率最多相差12.5%,这表明使用ST-GWNN辨识特定的操作动作具有相当大的优势,而且其准确性也体现了手势动作识别和异常行为检测的可能性。由于超参数s与节点间的相关程度成正比,随着s的增大,邻接节点的范围也在扩大,因此通过调整超参数s就能灵活控制邻域范围。图卷积在一定范围内融合邻接关节的有效信息越多,识别率越高。s增大到一定程度后,更大的邻域范围引入更多的噪声,使得识别率降低。从识别率波动下降的趋势可以看出,高阶的邻接节点的有效性是不太好确定的。例如在实验中,s大于0.5后,引入了更多的高阶邻点,识别率有所下降。超参数s为0.8和0.9时,邻域范围再次扩大,对应的识别率分别为70.80%和75.00%,由于引入了新的高阶邻点,识别率有所回升。此外,在进行数据集预处理时,存在无法提取关节坐标以及关节错位等问题,这表明输入的张量存在大量的无效元素以及噪声,此时ST-GWNN依然保持着良好的识别率,并能通过超参数s进行优化。
4 结束语
本文在图小波卷积核的基础上进行参数化处理,并利用一阶切比雪夫多项式来逼近卷积核,由此提出一阶时空图小波神经网络ST-GWNN。相对于原有的GWNN[19],一阶切比雪夫图小波的参数数量与节点个数n无关,这使得模型更加灵活,极大地减少了模型的学习参数。此外,ST-GWNN是通过调节超参数s而非多项式的阶数来控制邻域范围,在一定程度上克服了多项式阶数既定的情况下,卷积表现力不足的问题。
实验结果表明,在一定范围内调节超参数s可以提高动作的识别率,使得ST-GWNN具有更高的柔性。此外,将ST-GWNN应用于生产动作的识别上,并监控既定的违规行为,与ST-GCN相比,其识别效果更佳,这也表明将ST-GWNN运用到生产过程中具备可行性。
ST-GWNN仍然存在提取的关节信息噪声大的问题,这也是今后改进的方向。针对提高识别率,有以下两个改进方向:1)针对神经网络本身进行改进,如在深度网络中添加更多策略,以提高模型的识别能力;2)提高关节特征提取的精度,减少输入信息的稀疏性和噪声。值得一提的是,生产过程的环境通常较为恶劣,这对骨架图的提取极具挑战性,这也是动作识别能否实际应用于生产过程检测和事故预警的主要问题之一。

