相控阵雷达天线局部模态截断*

芮 棽

（南京电子技术研究所，江苏南京210039）

引 言

常用的动力学仿真计算方法有模态叠加法、直接法、Ritz法等[1-3]，其中模态叠加法是工程应用中最常用的方法。为了保证计算精度和计算效率，在应用模态叠加法时必须合理地进行模态截断。传统方法只需要计算较低的前几阶或某一频率范围的模态，用于近似地分析系统的动力响应[4]。文献[5]将势能判据截断准则应用到地震响应分析问题中；文献[6]研究了基于模态应变能的结构模态截断方法；文献[7]根据位移、速度和加速度响应选择合适的模态截断指标；文献[8]研究了移频技术在子结构低阶主模态截断中的应用；文献[9-10]通过模态综合法将准静力模态应用到坐标变换中，实现主模态截断。对于仅由非承力构件产生的局部模态，上述截断方法均不是最优方法。本文提出应用模态综合法对非承力构件产生的局部模态进行截断。

模态综合法[11-12]在复杂结构有限元仿真计算中有大量的应用[13]。工程中通常取子结构的若干阶低阶模态参与综合，考虑界面协调条件后，使广义坐标数进一步减少[4]。复杂结构中非承力构件往往数量多，易产生大量局部模态，而整体模态与局部模态通常交替出现，采用传统模态叠加法进行动力学仿真计算时无法直接对局部模态进行有效截断。通过模态综合法，将非承力构件设置为子结构，仅考虑其约束模态而忽略其动力特性，以此进行动力学仿真计算既能够保证计算精度，又可以大幅提高计算效率。模态综合法分为自由界面法[13]、固定界面法[14]与混合界面法，其中固定界面法适用于相控阵雷达天线结构的动力学仿真计算。本文研究基于固定界面的模态综合法，将相控阵雷达天线的子阵结构作为子结构处理，通过数值仿真研究验证了局部模态截断的准确性。

1 模态叠加法

n自由度结构动力学方程可以表示为：

式中：t和τ表示时间；ωd,i为第i阶模态的阻尼频率。

由式（4）、式（5）可知，复杂系统中如果有大量局部模态参与计算，计算效率将非常低。传统的模态截断方法通过选取较低的前r(r ＜n)阶模态或某一频率范围的模态来近似分析系统的振动响应。最终所选模态为一串连续的模态，无法将局部模态从所选模态中分离出来。模态选取结果为：

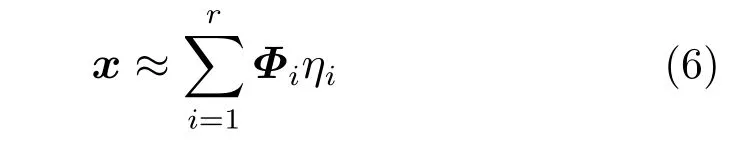
当主模态频率与局部模态频率交错出现时，该方法无法区分局部模态，而计算过程采用全部主模态时，必将计算大量局部模态。因此，传统的模态截断法对于某些复杂结构并不适用。

2 基于固定界面模态综合的局部模态截断法

将部分结构设置为子结构，该部分的约束模态方程可以表示为：

式中：Φe为局部结构模态向量；Φg为剩余结构模态向量。在局部模态下，Φg≪Φe。

当产生局部模态的部分为非承力结构时，其对计算结果的影响可以忽略。将局部模态自由度设置为子结构内部自由度，仅计算其静力变换矩阵，忽略动力变换矩阵，则在计算整体结构模态时，既保留了子结构的连接刚度，又消除了局部模态的影响。模态方程可以表示为：

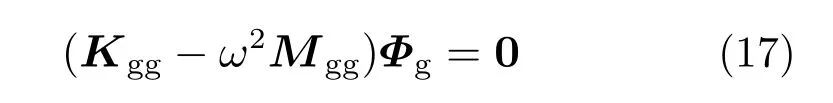
3 仿真研究

某雷达天线阵面结构有限元模型由骨架结构及子阵结构组成，见图1和图2。阵面骨架为主承力结构，共安装42个相同的子阵结构。骨架结构由平面四边形单元、三角形单元、六面体单元和梁单元组成，包含31 130个单元和29 789个节点。子阵结构由平面四边形单元组成，包含12 704个单元和14 488个节点。材料密度ρ=2 700 kg/m3,杨氏模量E=71 GPa，泊松比μ= 0.33。每个子阵通过两侧螺钉和底部插销与骨架相连，子阵之间相互独立，因此易产生大量局部模态。

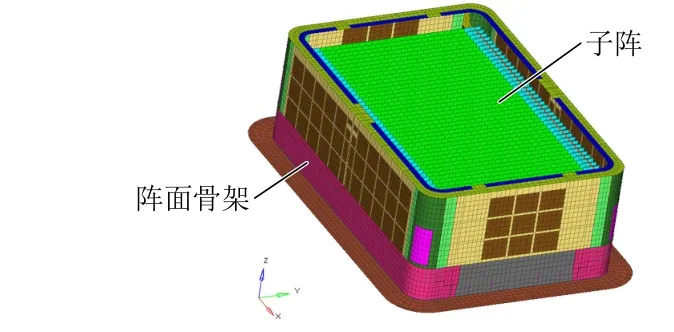
图1 有限元整体模型

图2 有限元局部模型

将所有子阵设置为子结构，外部节点为子阵与骨架的连接点。不考虑子结构的动力特性，计算结构500 Hz以内的所有模态，同时计算原结构500 Hz以内的所有模态以做对比。仿真结果如表1所示，部分模态振型云图如图3所示。

表1 模态计算结果 Hz

图3 振型云图

对比原结构和子结构的计算结果可知：1）对于子阵独立的局部模态，即180.6～181.1 Hz之间的所有模态，模态综合法可将其完全消除；2）对于子阵和骨架的耦合模态，即299.6～305.4 Hz和441.8～455.8 Hz之间的模态，模态综合法仅保留骨架部分的计算结果。

由模态分析结果可知，原结构计算模型中，子阵的局部模态和骨架的模态交替出现，500 Hz以内的模态数共计150阶，计算自由度包含所有节点自由度；子结构计算模型中，仅出现骨架模态，500 Hz以内的模态数共计66阶，计算自由度仅包含骨架结构中的节点自由度。在采用模态叠加法进行动力学计算时，子结构模型中参与计算的自由度和模态阶数均比原结构规模小，因此可大幅提高计算效率。采用相同的计算机配置计算天线阵面3个方向的加速度频率响应，原结构耗时32 min 17 s，子结构耗时9 min 52 s，各方向加速度最大值响应结果如图4所示。计算结果表明，采用模态综合法的骨架结构加速度响应计算结果与原结构相同，同时计算效率得到大幅度提高。

图4 加速度响应曲线

4 结束语

相控阵雷达天线结构的模态分析中包含大量来源于子阵结构的局部模态，利用模态综合法将所有子阵结构作为子结构处理，计算结构整体刚度矩阵时仅考虑其连接刚度而忽略其动力特性，可以完全消除子阵结构的局部模态。由模态分析结果可知，利用模态综合法截断子阵结构局部模态的同时保证了其余结构的模态与原结构模态相同。由加速度响应分析结果可知，对于其余结构部分，模态综合法的计算结果与原模型计算结果完全相同，且计算时间大幅减少。

利用模态叠加法进行动力学仿真计算时，对于由非承力构件引起的局部模态，采用模态综合法，将对计算结果影响较小的局部模态部分的结构设为子结构，通过缩聚方式保留其与主体结构连接的刚度特性，同时舍弃其自身动力特性。该方法不仅可以缩减参与计算所需的模态阶次，还能缩减局部模态部分的自由度，在保证计算精度的前提下极大地提高了计算效率。