基于二维DFT的钢丝绳局部缺陷检测方法*
杨磊磊,刘志亮,,郭嘉树,左明健,3
(1. 电子科技大学机械与电气工程学院,四川 成都611731;2. 电子科技大学格拉斯哥学院,四川 成都611731;3. 青岛国际院士港研究院,山东 青岛266041)
引 言
钢丝绳因其材料的延展性及其捻向结构设计,具有高强度、高韧性等特点,在承受张力等方面表现优良,因而被广泛应用在工程和生活的各个领域[1]。然而,经长期使用后,钢丝绳的钢绞线难免出现磨损、老化、锈蚀,甚至部分断裂,影响到设备及人员安全,因此钢丝绳的在线无损检测至关重要。
根据损伤的性质及程度,钢丝绳损伤主要可分为两大类:局部损伤(Local Flaw, LF)和横截面积损失(Loss of Metallic Area, LMA)。无损检测因其非破坏性的优点,近年来逐渐受到重视[2]。国内外针对钢丝绳的无损检测开展了大量研究。根据不同的检测原理,钢丝绳无损检测采用光学、声学、电磁等不同检测方法[3-5]。其中,光学方法虽然能够直观展现钢丝绳的表面图像,但因钢丝绳所处环境复杂及表面油污干扰,在实际工况下往往难以获得良好效果。声学法(如超声及声发射等方法)通过检测声波变换来判别断丝及钢丝绳变形等损伤,但信噪比普遍较低。这两类方法都难以检测钢丝绳内部的损伤,因此电磁方法以其良好的定性判断损伤类型及定位损伤位置的性能广泛应用在钢丝绳无损检测领域。为提升传感器的检测性能,大量基于电磁检测原理的钢丝绳无损检测传感器结构设计及理论研究逐步得以开展。例如,文献[6]采用低频透射式电涡流检测方法,设计出一套探头沿径向对称布置的可调式环形涡流钢丝绳探伤装置;文献[7]提出基于隧道磁阻传感器的漏磁检测传感器,可以检测直径为0.5 mm的单根断丝。此外,目前许多商业传感器已经应用到实际场景中,如国外NDT tech.公司研发的LMA系列探伤仪、波兰Zawada NDT研发的MD系列探伤仪等[8]。然而有报告表明,市面上钢丝绳无损检测仪器的性能在钢丝绳损伤检测方面仍有较大改善空间[9]。
在传感器检测性能优化的同时,由于电磁检测方法受到钢丝绳股波信号、周围环境噪声及抖动等因素的干扰,钢丝绳电磁无损检测信号往往难以直接提取损伤特征。为此,近年来逐渐提出了不同信号处理和损伤识别方法。文献[10]较早介绍了钢丝绳漏磁信号的部分预处理和滤波技术;文献[11]设计了参数自适应的空间滤波器,用于抑制钢丝绳股波信号。之后,文献[12]利用灰度共生矩阵方法提取图像的纹理特征,进行漏磁信号故障特征提取;文献[13]建立了等效磁偶极子模型,在数据处理上运用小波对漏磁数据进行降噪,验证了小波方法的去噪效果;文献[14]和[15]则通过对钢丝绳断丝轴向漏磁场进行有限元仿真分析,验证基于磁荷模型的理论分析结果,并采用双密度双树复小波变换和逆向传播(Back Propagation, BP)神经网络对钢丝绳损伤进行识别;文献[16]采用基于希尔伯特变换的包络方法,提升漏磁信号的信噪比。
上述研究多采用基于一维漏磁信号的检测方法,通过分析其时频域指标提升漏磁信号的信噪比,进而确定缺陷属性。但由于一维信号只包含缺陷信号的幅值、频率等独立特征信息,因而不能综合空间信息判别同一位置处集中断丝与离散断丝的区别,难以满足损伤检测的需求[17]。因此,有人提出了利用传感器的空间分布特征,将漏磁信号转化为二维图像甚至三维信息的处理方法。文献[18]曾对周向插值后的二维漏磁图像进行处理,通过漏磁图像二值化后的局部像素和对应缺陷大小进行定量分析;文献[19]也通过将漏磁信息转化为二维漏磁图像,分析抖动信号及股波信号的时频特征,通过斜向重采样及零相滤波器有效滤除了股波噪声,提升了缺陷信号的信噪比。在此基础上,文献[20]通过建立钢丝绳抖动模型分析了由抖动造成的提离值不同对漏磁信号的影响,所提出的一种基于环形中值滤波的抖动抑制方法,在复杂情况下具备更强的鲁棒性并取得了良好的缺陷提取效果。
综上所述,二维漏磁图像可提供空间信息及多场点漏磁场信息(一维信号却没有此功能),处理后所提取的特征量能够作为损伤分析模型的参数,同时漏磁信号中的空间特征为准确提取损伤特征值和空间位置提供了判定依据。虽然漏磁图像用于缺陷提取取得了较好效果,但目前针对漏磁图像中股波的去除算法流程仍较复杂,处理时间较长,难以应用到大量数据的实时处理中。因此,本文提出一种基于二维离散傅里叶变换(Two-dimensional Discrete Fourier Transform,2D-DFT)的信号处理方法,对一维漏磁信号进行预处理后再转换为二维漏磁图像,进行二维离散傅里叶变换后,通过设置滤波器对漏磁图像进行处理。本文主要贡献如下:
1)首次从二维频域上分析漏磁信号特征,并直接使用图像处理方法对钢丝绳漏磁信息进行分析处理;
2)明确了漏磁图像中股波的频域分布特点,并提出基于2D-DFT的漏磁图像局部缺陷检测算法。
1 信号采集与处理方法
1.1 漏磁传感器设计及信号采集
本文采用霍尔元器件阵列来检测钢丝绳表面磁场变化,从而获取钢丝绳损伤处的漏磁信号。用于钢丝绳损伤检测的漏磁传感器结构如图1所示。它包含外壳、励磁部分与检测部分。其中励磁部分由永磁体和衔铁构成,用于饱和磁化检测区域的钢丝绳;检测部分包含霍尔传感器阵列及数据采集卡。

图1 漏磁传感器
在实验过程中,为保证漏磁传感器能够有效饱和磁化钢丝绳,产生稳定的漏磁场,永磁体采用剩磁可达1.4 T的钕铁硼材料(N50),其磁能积可达到382~398 kJ/m3。衔铁采用高磁导率的电工纯铁材料(DT4C),16个霍尔传感器作为检测部件,均匀分布在钢丝绳外圈的周向位置,霍尔传感器之间相隔22.5°。漏磁传感器的采样频率为2 500 Hz,数据采集卡将采集到的径向漏磁信号传输至上位机。实验过程通过滑块或手动移动传感器,使传感器检测整段钢丝绳的损伤状态。工字钢支架用于固定钢丝绳位置,模拟实际工况下对钢丝绳的检测,如图2所示。实验中在长度为1.7 m的钢丝绳上人工制作2处LF损伤。检测过程中励磁模块饱和磁化钢丝绳,当传感器通过缺陷位置时钢丝绳表面产生磁场变化,霍尔元器件能够检测到漏磁场的变化,从而获取漏磁信号,用于后续损伤特征的判定和提取。

图2 试验台实物图
1.2 基于二维傅里叶变换的信号处理方法
由于钢丝绳损伤具有轴向、径向及周向特征,单路霍尔传感器采集到的信号难以表征缺陷全貌。为提升钢丝绳损伤分辨率,可将多路一维信号经插值处理后形成二维图像信号,进而提取漏磁信号中的缺陷空间分布特征。对二维图像进行多分辨率处理时,二维离散傅里叶变换方法能够描述图像的频率属性,因而可从频域滤除股波及其他低频噪声。因此本文选用二维离散傅里叶变换作为图像处理的基础工具。
二维傅里叶变换通过将图像从空间域转换为频域,能够直接表征图像中像素的灰度变化剧烈程度。设尺寸为M×N的图像f(x,y),其中,M为图像的宽度,N为图像的长度,x= 0,1,··· ,M- 1,y=0,1,··· ,N-1,其二维离散傅里叶变换后的图像F(u,v)可表示为:
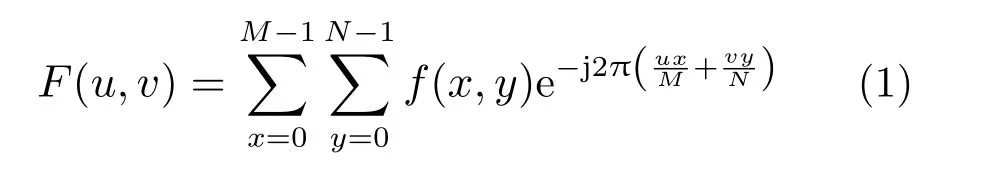
式中:u= 0,1,··· ,M-1;v= 0,1,··· ,N-1。在默认情况下,以图像左上角作为图像原点,由式(1)可知,频谱作为图像信息分布的一种表现形式,具有中心对称的特性,其低频部位代表图像中的平滑元素,高频处代表突变及边缘等区域。
根据本文提出的方法,通过二维离散傅里叶变换将漏磁图像转化为频域后,为检测LF信号,需对不同噪声对应的频率分量进行滤除处理。如图3所示,整个处理流程可分为3个步骤,即漏磁信号预处理、漏磁图像降噪及LF定位。预处理包含通道均衡及通道插值等操作,完成从一维信号到二维漏磁图像的转换;漏磁图像降噪处理通过二维离散傅里叶变换将漏磁图像变换为频域,并通过设置滤波器滤除背景噪声和股波噪声等,从而提升重构图像中缺陷的信噪比;最终通过阈值设置,完成重构图像的二值化处理,提升缺陷的对比度并提取LF位置信息。
2 实验信号分析
2.1 漏磁信号预处理
实验中,由于冗杂噪声信息会影响后续图像处理及特征提取,因此为改善图像细节,增强图像质量,需对图像进行预处理。本文主要采用通道均衡和通道插值方法对原始信号进行预处理。实验中采用的霍尔传感器的灵敏度为1.4 mV/Gs,可将采集到的电压信号转换为磁场变化。图4展现了钢丝绳表面漏磁场的变化趋势。当钢丝绳与传感器产生相对运动时,由于钢丝绳表面呈凸凹不平的捻制结构,所以它将采集到周期的股波信号。在实验过程中,由于漏磁传感器内部霍尔传感器存在个体差异且距离钢丝绳的提离值不同,因此每路漏磁信号并不在同一基线上。为消除外部噪声及基线差异,首先需要对原始信号进行通道均衡处理。如图5所示,通道均衡后的信号能够消除信号偏移对后期缺陷识别的影响。
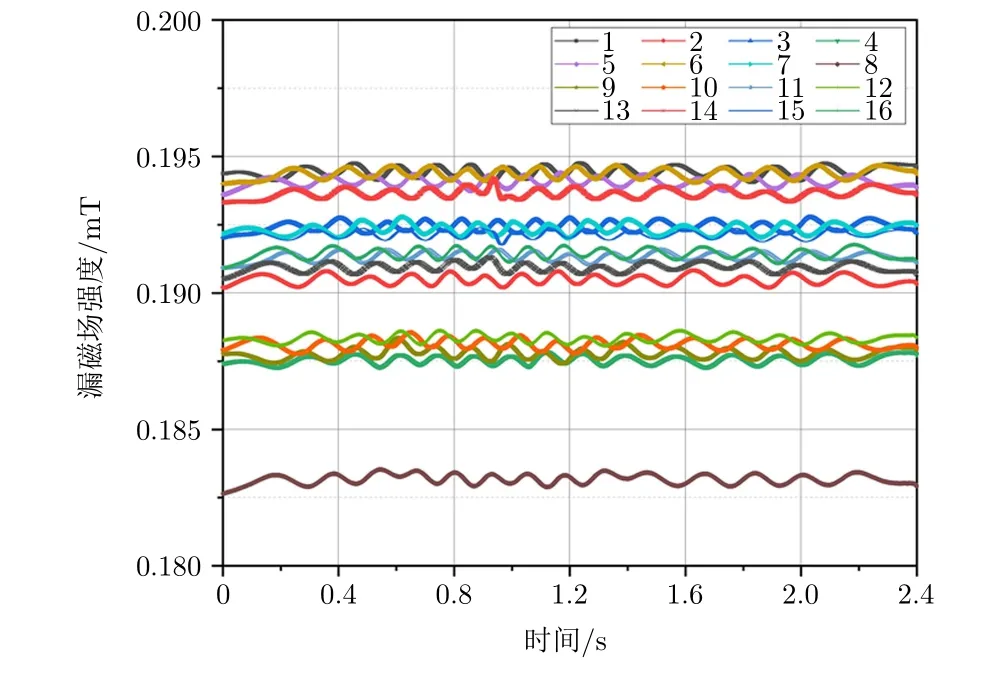
图4 漏磁传感器采集的16路漏磁信号
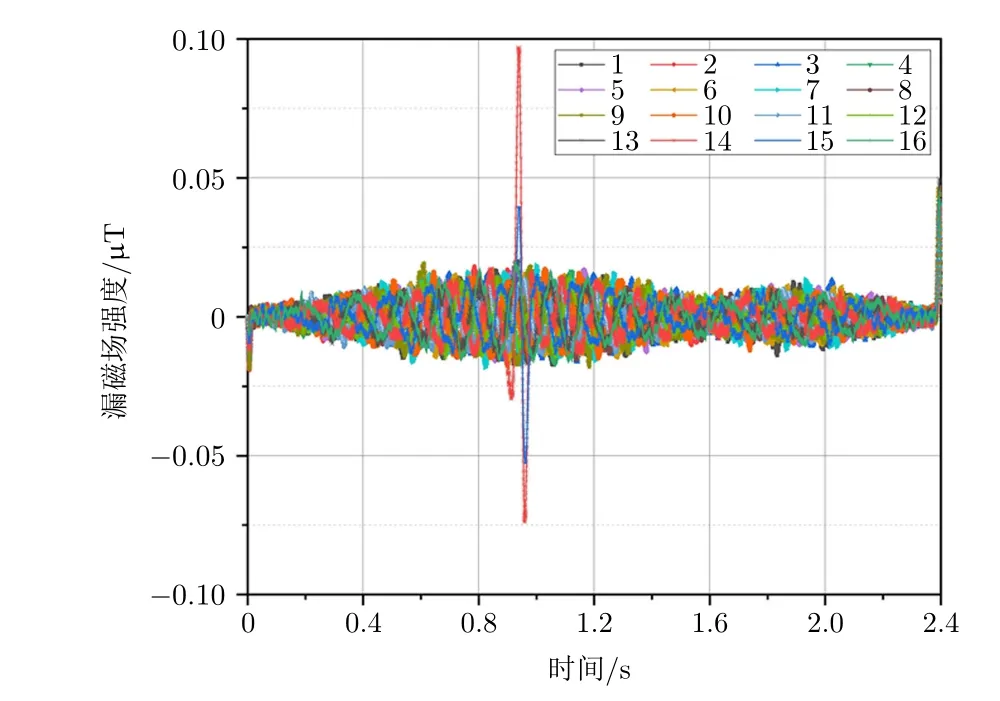
图5 通道均衡后的16路漏磁信号
然而,若直接将16路漏磁信号显示为漏磁图像,则缺陷信号因图像分辨率较低而难以区分。本文采用样条插值方法对信号进行数据扩充,提高漏磁图像的分辨率。将16路漏磁信号插值为360路信号后,漏磁信号可转换成如图6所示的漏磁图像信号,可体现其周向信息,并能有效分辨信号中所含的股波等信号。

图6 通道插值形成漏磁图像
2.2 漏磁图像降噪
傅里叶变换作为频域处理的经典算法,能够快速完成图像的时频域转换。由于钢丝绳漏磁信号中股波噪声及背景噪声为典型的低频信号,因此可对漏磁图像信号进行二维离散傅里叶变换后,选用合适的高通滤波器消除低频噪声信号影响。漏磁图像的频谱范围较大,且中心亮度处于支配地位。为分析频谱细节,将频谱中心化后使用对数变换提升对比度。处理后的频谱如图7所示,频谱中亮点对应了漏磁图像中的周期性结构。漏磁图像中股波及背景噪声为低频信号,导致频谱中有效信息集中在中心处。图7对中心处的细节进行了放大处理,便于对比频谱处的细节特征。
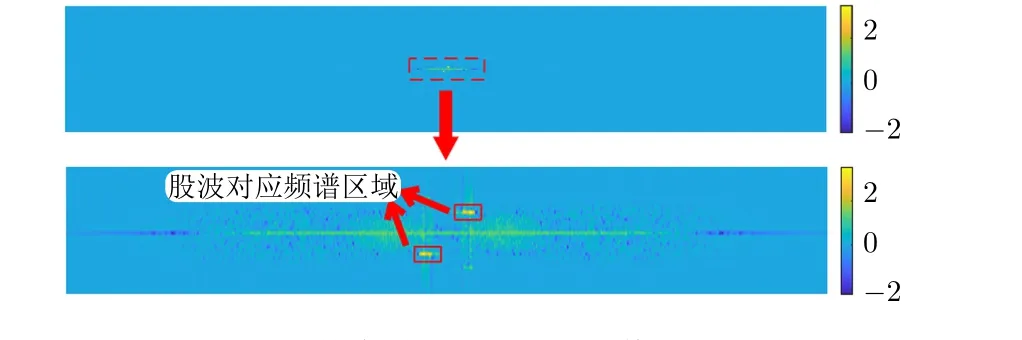
图7 用对数变换增强的可见谱及其放大图
由于巴特沃斯滤波器在通带内具有良好的平坦特性,因此本文为滤除低频噪声和提取漏磁图像中的缺陷信号,采用二阶巴特沃斯高通滤波器,能够在滤除噪声的同时锐化漏磁图像。n阶巴特沃斯高通滤波器传递函数可定义为:

分析钢丝绳漏磁信号的频谱时,本文通过设计合适的高通滤波器滤除噪声对应的低频分量。将高通滤波后的频谱零点平移至图像中心后,中心处局部频谱细节如图8(a)所示。高通滤波后频谱图像中的低频分量及直流分量能够被有效滤除,从而消除图像空域中变化平缓的图像噪声。高通滤波后的漏磁图像如图8(b)所示。
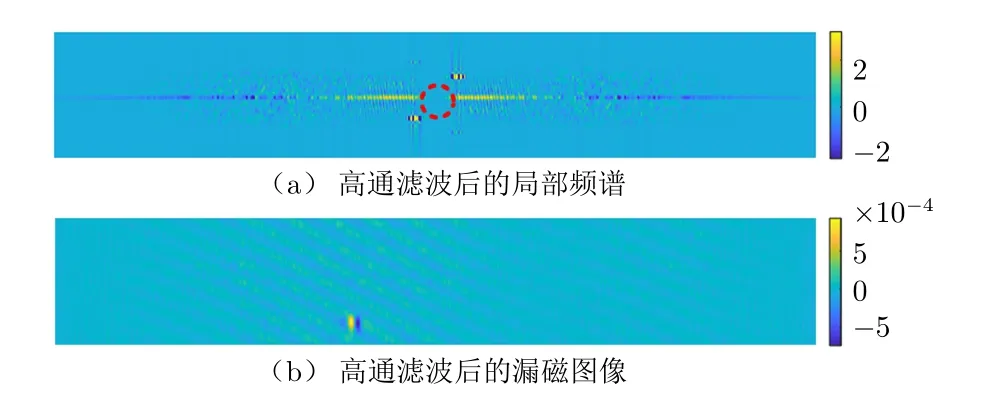
图8 高通滤波后的局部频谱及对应的漏磁图像
滤除图像中存在的低频噪声后,股波噪声成为影响LF定位的最大因素。因钢丝绳独特的捻制结构,钢丝绳被饱和磁化时,其表面会形成规律的漏磁场,体现为漏磁图像中的股波纹路。股波是由霍尔传感器阵列与钢丝绳的相对运动造成的,因此股波斜率与两者间的相对速度有关,呈现出一定的频率范围。当缺陷较小时,漏磁信号易被股波信号掩盖,因此股波信号的滤除在二维漏磁图像处理中至关重要。本文通过构建二维陷波滤波器针对漏磁图像频域上的股波频率段进行滤除。如图9(a)所示,很明显中心处局部频谱中股波对应的较强频谱成分已被滤除。通过对处理后的二维信号频谱进行反变换,重构图像,如图9(b)所示。缺陷信号与背景对比明显,并且对股波信号进行了有效抑制。
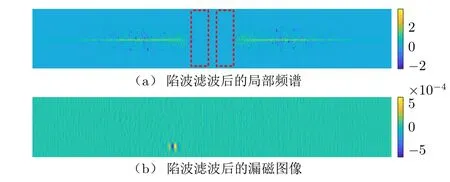
图9 陷波滤波后的局部频谱及其对应的漏磁图像
2.3 LF定位
重构图像后股波及低频噪声被基本滤除,为清晰地分辨图像中的缺陷信号,可进行二值化处理以进一步提升图像中缺陷的对比度。由于漏磁传感器在采集钢丝绳表面漏磁场时,磁场方向会在缺陷两端发生变化,导致缺陷信号产生波动,因此在进行二值化处理前可对图像进行包络处理,使得缺陷信号的能量集中。同时,信号能量集中后获取的包络图有利于二值化阈值的设定,减少缺陷的误判率。如图10所示,二值化处理后的结果能够有效分辨缺陷信号及缺陷位置。通过将二值化后的数据投影到水平和垂直方向上,寻找二值化图像中元素为1的坐标,便可判断此处缺陷出现在0.918~0.946 s这一时间段,角度在286°~309°范围内。

图10 二值化处理后的漏磁图像
3 方法对比及讨论
3.1 基于一维离散傅里叶变换的缺陷提取方法
本文采用基于2D-DFT的方法对钢丝绳表面缺陷进行了处理,为验证二维方法的有效性,与一维离散傅里叶变换的处理效果进行对比。文献[21]曾利用一维离散傅里叶变换和陷波滤波器对漏磁信号进行了处理,将漏磁信号转化为频域后,通过计算股波频率,利用一维陷波滤波器滤除股波。以图4中的数据为原始数据,滤除后的漏磁信号如图11所示。图12展示了通道14的漏磁信号在滤波前后的低频部分频谱变化。虽然使用一维陷波滤波器能够滤除幅值较大的股波频率,但时域上仍存在微弱的股波轮廓未能完全滤除。同时,使用一维离散傅里叶变换直接滤除后缺陷信号的信噪比较低,不利于缺陷的识别和提取。如图13所示,采用本文所提方法,进行预处理步骤的通道均衡处理后,才能获得较好的缺陷识别效果。
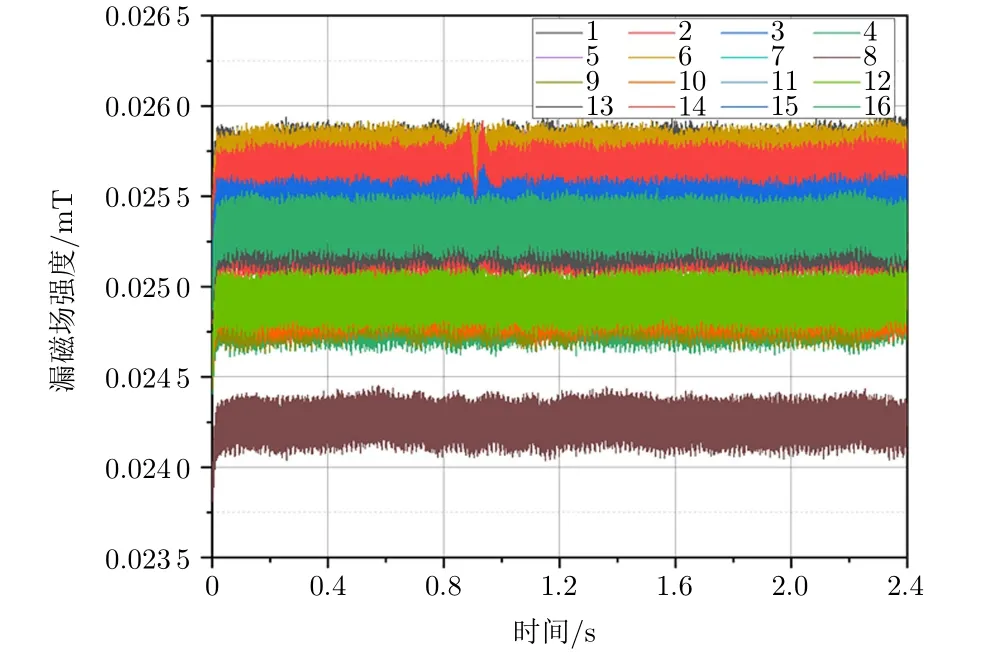
图11 一维DFT滤波后的漏磁信号
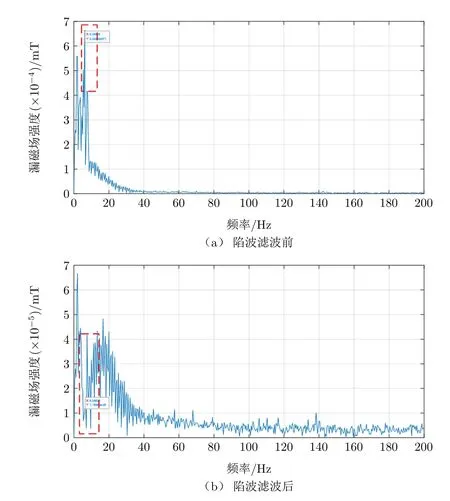
图12 陷波滤波后通道14漏磁信号的局部频谱
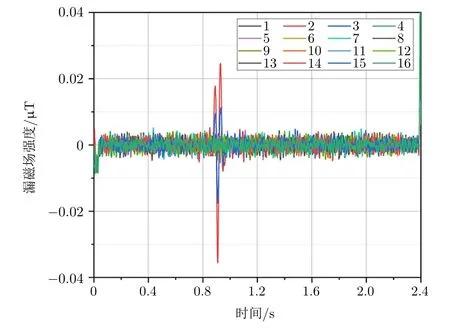
图13 漏磁信号陷波滤波后进行通道均衡的处理结果
与二维漏磁图像处理方法相比,基于一维离散傅里叶变换的方法直接采用陷波滤波器虽能够提取到缺陷信号,但因股波频率较低,难以在频谱中定位,因而需要通过信号中股波周期进行计算,导致股波滤除效果并不理想。同时,一维漏磁信号只含有所采集漏磁信号的径向分量,损失了钢丝绳损伤的周向信息,因而难以满足损伤分析的需求,不能有效分辨同一位置上集中断丝和分散断丝的差异。
3.2 基于斜向重采样的缺陷提取方法
为分析本文所提方法的处理效果,将它与漏磁图像的其他股波处理及缺陷提取方法进行对比。文献[19]提出一种基于斜向重采样的股波滤除及缺陷信号提取方法。如图14所示,该方法包括6个关键步骤:通道均衡、通道插值提升周向分辨率、股波去除、抗抖动滤波、缺陷能量集中和二值化。该方法通过斜向对数据重采样进而消除股波对应图像中的斜向条纹。由于斜向重采样后股波和缺陷信号在频域上有显著差异,因此重采样后利用零相滤波器滤除股波。最终通过仿真和实验,验证了该方法对股波信号的良好处理效果,并有效提取出缺陷形态。值得一提的是,虽然其最终结果以二维图像方式呈现,但在降噪处理上仍是以多路一维信号为对象,并未使用漏磁图像的特征及对应的图像处理方法。
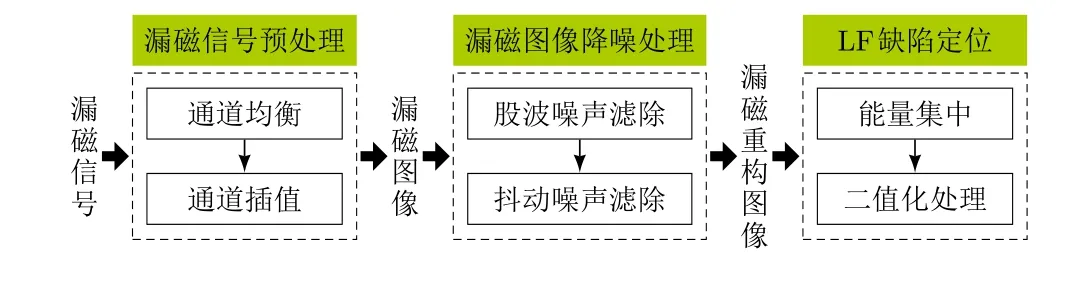
图14 基于斜向重采样的股波滤除及缺陷信号提取法流程图
针对图4中的钢丝绳表面漏磁数据,采用基于斜向重采样的股波滤除及缺陷信号提取法进行处理,以对比两种方法在不考虑抖动干扰时的算法差异。用两种方法提取的缺陷信号在同种颜色图尺度范围内,如图15所示。经对比,这两种方法都能够有效提取到缺陷信号,并且对股波信号都有良好的滤除效果,但从图像背景纹理来看,采用本文所提的方法,噪声滤除得更彻底,同时由于处理方式不同,在对两种方法重构图像进行分析时,仍发现有部分参数存在差异。如图16所示,在信号处理过程中,两种方法都曾对重构后图像取其包络进行二值化处理。以其重构图像包络信号的信噪比RSN作为一项对比指标,将其定义为:

图15 两种方法的漏磁重构图像
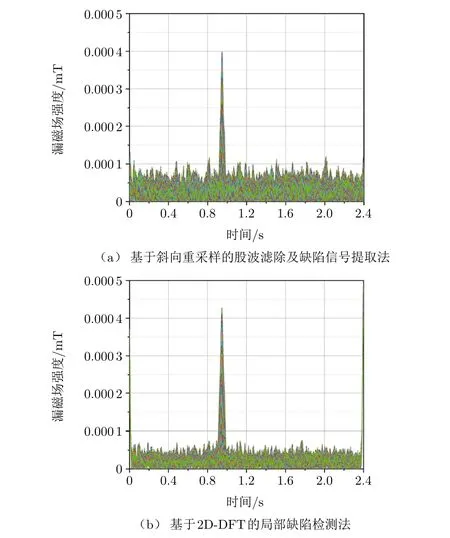
图16 两种方法的重构信号包络图
通过两种方法的信号处理速率以及重构图像包络信号的信噪比两个指标的对比(见表1),可得出以下结论:
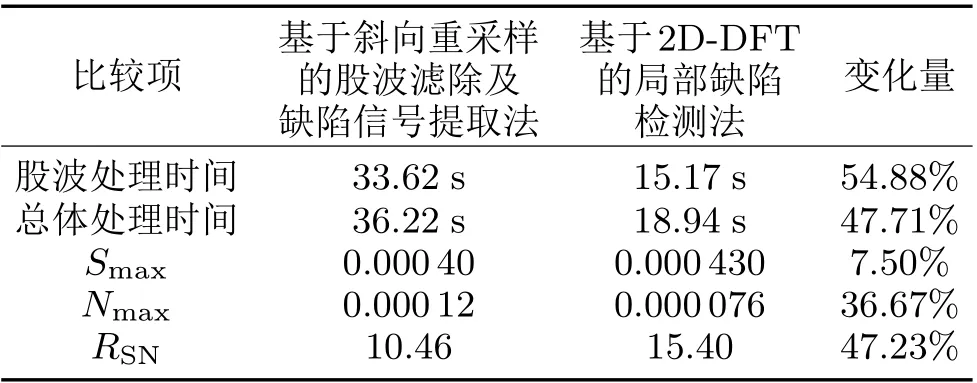
表1 两种处理方法的性能比较
1)在信号处理速度方面,采用本文的方法,滤除股波耗时15.17 s,而采用基于斜向重采样的股波滤除及缺陷信号提取法,滤除股波耗时33.62 s。前者所用时间比后者缩短了54.88%,整体处理时间降低了47.71%,在针对大量数据时具有明显优势。
2)在信噪比方面,采用本文的方法,重构图像的包络图无论是在信号强度或噪声水平上都有所改善,与利用斜向重采样方法的10.46 dB相比,其信噪比提升了47.23%,更利于信号的提取及缺陷判别。
4 结束语
本文通过将钢丝绳损伤漏磁信号转换为二维图像信号,提出一种基于二维离散傅里叶变换的信号处理方法,用于提取局部缺陷特征。利用高通滤波器及陷波滤波器滤除图像中的背景噪声及股波噪声,并与基于一维离散傅里叶变换的陷波滤波处理方法和基于斜向重采样的二维漏磁图像处理方法进行了对比。通过实验数据处理,相较于基于斜向重采样方法,采用本文所提方法,其信噪比提升了47.23%,并且股波滤除处理时间缩短了54.88%,验证了所提方法在股波噪声抑制能力和处理速度上的优势,为钢丝绳在线无损检测的信号处理、损伤特征提取及定位提供了新的思路和方法。

