基于SVM分类器的癫痫脑电时空特征提取方法的研究
易芳吉,钟丽莎,李章勇
(1.重庆邮电大学 生物信息学院,重庆 400065;2.西南医科大学 医学信息与工程学院,四川 泸州 646000;3.厅市共建中枢神经系统药物四川省重点实验室,四川 泸州 646000)
0 引 言
癫痫是仅次于脑卒中的常见神经系统疾病,据世界卫生组织报道[1],癫痫患者约占全世界人口的1%,其中80%的患者来自发展中国家,我国的癫痫患者数量高达900万。每年全世界治疗癫痫的费用约为12.5亿元,调研显示,近年来我国未接受过癫痫治疗的患者比例超过60%。目前癫痫发作涵盖各年龄段,严重影响人类大脑健康,特别是对小孩智力造成不可逆转的伤害。并且癫痫可以在任何环境,毫无征兆地发作,易发生各种意外事故,严重的可能导致死亡。由于癫痫发作的不确定性,癫痫患者需要长期服药,对其身心带来较大的伤害。因此,分析和挖掘癫痫特征有助于实现癫痫发作预警,不仅可以保障患者人身安全,还可以为患者选择紧急抗癫痫药物治疗提供依据。
脑电图(electroencephalogram,EEG)反映大脑神经元放电活动,因其价格便宜,且时间分辨率较高,广泛地应用于癫痫发作预测。癫痫发作预测本质是分类癫痫发作前期和发作间期脑电信号,由于癫痫脑电发作前期不像发作时具有明显的高频高幅特征,而且个体之间存在较大差异,甚至同一个体的多次发作都存在差异,因此目前癫痫发作预测方法仍然面临较大挑战。癫痫发作预测的效果由选取的特征参数决定,如何提取有效的癫痫特征信息成为众多学者的研究焦点。随着计算机技术的发展与脑电信号数据的不断增加,国内外学者基于机器学习对癫痫特征的提取开展了大量的研究。文献[2]提取多通道脑电的皮尔逊相关系数,使用卷积神经网络(convolutional neural network,CNN)对相关矩阵进行分类识别,区分发作前期和发作间期的脑电信号,准确率为89.98%。文献[3]利用互相关估计脑电通道之间的同步性,基于该特征预测癫痫发作,平均灵敏度为84%,特异性为63%。文献[2-3]的准确率较低,其原因可能是提取的特征都是单一通道间的同步特征。大脑是一个非线性系统,产生的脑电具有非线性特征。熵具有非线性特征,有学者提出“熵脑假说”,认为熵可以反映大脑活动的不确定性[4]。有部分学者提取各类熵应用于癫痫脑电特征分析,取得了较好的效果。文献[5]使用排列熵作为癫痫特征,运用支持向量机(support vector machine,SVM)识别癫痫发作样本,其81%的发作可以提前50分钟预测到。文献[6]提取单导联癫痫脑电的模糊特征,对癫痫脑电进行预测,达到80.2%的准确率和86.5%的特异性。虽然空间同步特征、非线性熵特征都能进行癫痫的发作预测,但只考虑时序特征或空间特征的癫痫预测算法准确率仍然不够理想。癫痫脑电不仅呈现高频高幅的时序特征,同时还具有较强的空间同步耦合关系,因此,从时空关系角度可以充分挖掘癫痫信息,提高癫痫发作预测效果。
本文联合时间和空间两个维度,提出了一种基于SVM分类器的癫痫脑电时空特征提取方法。该方法提取模糊熵,从时序特征角度评估脑电信号复杂度;提取皮尔逊相关系数,从空间特征角度评估脑电各导联之间的相关性;提取时空特征信息,有助于实现临床癫痫发作预警。
1 研究方法
本文的算法流程如图1所示。首先,对脑电信号进行预处理;然后,提取特征参数,利用F-score进行特征筛选,选出最优特征组合;最后,将SVM分类器应用到癫痫脑电中,识别前期和间期,实现癫痫发作预测。

图1 基于时空特征癫痫预测流程图Fig.1 Flow chart of epileptic prediction based on temporal and spatial feature
1.1 预处理
脑电信号微弱,且易受外界干扰。小波滤波在最大限度保持真实信号的基础上,减少甚至完全滤除噪声。db小波[7]分解既可以分解信号中低频部分,也可以分解高频部分,能调整频域分辨率使之与脑电节律相一致。因此,db小波更适合用于处理脑电数据,本文采用db4小波去除信号的噪声干扰。癫痫脑电切割片段长短会影响预测效果,使用非重叠滑动窗的方式将原始脑电数据分割成20 s的片段。其原因是癫痫发作前产生的癫痫样放电一般持续时间在几秒到十几秒之间,20 s包含整个癫痫样放电发作时间。
1.2 特征提取
癫痫特征参数是决定准确率的关键因素,由于脑电信号的非线性和不确定性,可以将其看作一个模糊集,故选用模糊熵[8]度量脑电随时间变化的复杂度。选择皮尔逊相关系数度量导联间的同步性,具有算法简单、零迟滞、鲁棒性好的优点[9]。本文提取的特征参数集包含时间和空间二维特征。
1.3 特征筛选

1.4 支持向量机模型
SVM是一种监督学习的分类器,通过寻找一个超平面,能最大间隔区分数据[10]。SVM的优势在于最大化边缘区域的同时最小化经验误差,其决策函数和计算量由所选取的支持向量决定,这有助于剔除冗余样本,避免维数灾难等问题[11]。本文将癫痫脑电数据划分为训练集和测试集,通过网格搜索方法寻找最优SVM参数,然后根据训练集数据建立最优癫痫发作预测模型,区分发作前期和发作间期数据。为了使实验结果更准确,对同一被测试数据采用10折交叉检验,计算其平均准确率和误报率。
2 算法与原理
2.1 模糊熵
熵原本是热力学的概念,可以度量热力学系统的混乱程度,也可描述时序信号中新信息发生率大小。对于给定的时间序列[u(1),u(2),…,u(N)],模糊熵的计算步骤如下[12]。
1)定义相空间维数m(m≤N-2)和相似容限度r,重构相空间:X(i)=[u(i),u(i+1),…,u(i+m-1)]-u0(i),i=1,2,…,N-m+1
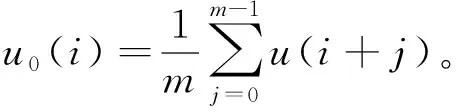
2)引入模糊隶属函数
(1)
当i=1,2,…,N-m+1时
j=1,…,N-m+1, 且j≠i


(2)

因此,有限时序数据集的模糊熵为
FuzzyEn(m,r,N)=lnΦm(r)-lnΦm+1(r)
(3)
(3)式中,相似容限r为0.2SD,SD为原时序信号的标准差[13],当m值较大时,能更好地描述重构时的动态演化细节。
2.2 皮尔逊相关性
皮尔逊相关性是指对两个或多个元素分析其相关性,从而衡量变量之间的相关密切程度。本文使用皮尔逊相关系数(Pearson’s correlation coefficient,PCC)来描述脑电导联间的同步程度。给定两个随机脑电通道X,Y,皮尔逊相关系数r的计算式为[14]
(4)
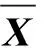
2.3 F-score的特征筛选
F-score是一种基于类间类内距离的特征重要性评价准则,可以有效衡量特征在实现二分类问题中对正确分类的贡献大小[15]。F-score的定义为
(5)
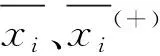
步骤1对所有特征进行F-score评价,并根据F-score的结果进行降序排列。
步骤2将特征子集设置为空集,全部特征设置为被选特征集。
步骤3当被选特征集不为空集时,选择第1个特征(F-score值最大)加入到特征子集中,同时在被选特征集中删除该特征。以特征子集构造分类模型,并得到准确率。
步骤4重复步骤3,若准确率提高,则在特征子集中保留该特征;否则,在特征子集中删除该特征,即舍弃该特征。
步骤5重复步骤4,直至被选特征集为空集,特征子集中的特征即为最优特征组合。
3 结果和讨论
本文的数据来源于kaggle竞赛[16](美国癫痫协会癫痫预测竞赛)颅内脑电图(intracranial electroencephalogram,iEEG)记录,数据采集自5只患有癫痫的犬类iEEG,采样频率为400 Hz,采用电极为16导联。该数据被癫痫学家标注为发作前期或发作间期。为了方便实验,将5只狗分别记为被试1—被试5。
3.1 预处理结果
脑电信号的数量级一般是微伏级,易受到噪声干扰。噪声会影响脑电数据的质量,对后续实验效果有较大干扰。通过db4小波6层分解重构后,癫痫脑电信号变得平滑,滤波结果如图2所示。

图2 小波滤波结果图Fig.2 Graph of wavelet filter result
3.2 模糊熵在发作前期与发作间期的比较
模糊熵可以衡量时间序列信号的复杂程度,对比研究癫痫脑电在发作前期和发作间期的模糊熵变化情况如图3所示。发作前期的模糊熵值普遍高于发作间期,只有少数区域重叠。发作前期的模糊熵值有较长时间的剧烈波动,越接近癫痫发作,模糊熵值越大,整体来看发作前期的模糊熵值呈现上升趋势。发作间期的模糊熵剧烈波动时间短,且上升趋势不明显。实验结果表明,模糊熵能够有效区分癫痫发作前期和发作间期。

图3 模糊熵在发作前期和发作间期的对比Fig.3 Comparison of fuzzy entropy of EEG between preictal and interictal stage
3.3 发作前期和发作间期的相关性对比研究
将皮尔逊相关系数绘制成邻接矩阵,用色块颜色直观表示导联间的同步性,色块颜色越靠近颜色栏上端,表明同步性越强。癫痫发作前期与发作间期的皮尔逊相关系数的对比如图4所示。皮尔逊相关系数大于0.6为强相关,小于0.4为弱相关。从图4可以看出,发作前期多数通道呈现强相关,发作间期多数通道属于弱相关。试验表明,发作前期和发作间期的导联间同步性存在明显差异,可以使用皮尔逊相关系数识别脑电信号的发作前期和发作间期。

图4 癫痫发作前期与发作间期的皮尔逊相关系数对比Fig.4 Comparison of Pearson’s correlation coefficients of EEG between epilepsy preictal and interictal stage
3.4 癫痫发作预测效果分析
为了验证本文时空特征预测癫痫发作的效果,选取准确率(accuracy,Acc)和误报率(false prediction rate,FPR)两个评价指标衡量预测结果。
准确率公式为
(6)
误报率公式为
(7)
(6)—(7)式中:TP代表真阳性(正类预测成正类)值;FP代表假阳性(负类预测成正类)值;FN代表假阴性(正类预测成负类)值;TN代表真阴性(负类预测成负类)值。
将本文方法分别与单一特征模糊熵和皮尔逊相关系数法进行对照实验,结果如表1所示。当仅使用模糊熵作为特征时,平均准确率为81.70% ,平均误报率为12.30%;单独空间特征的准确率为76.08%,误报率为7.5%;时空特征预测方法的准确率达91.26%,误报率仅为2.32%。因此,本文所提出的方法的预测效果优于单一特征,且准确率主要与模糊熵相关,而误报率主要受皮尔逊相关系数影响。

表1 分类准确率和误报率Tab.1 Classification accuracy and false positives %
采用本文的时空特征方法,被试3的准确率最高,但误报率也最高,被试5的准确率最差,而误报最少。结果表明,样本的准确率与误报率不是一致的,存在着准确率最优反而误报率最差的现象。被试1和被试5的准确率都低于90%,原因可能是癫痫发作次数比其他3个被试少,由于缺乏发作前期数据,样本量大小直接影响机器学习的准确率。被试3和被试4的准确率有较高的提升,但误报率却比只采用某单一特征参数的误报率高,其原因可能是算法为了得到整体最优预测效果,牺牲误报率来提高准确率。实验表明,本文方法可以平衡准确率和误报率两个指标,使得预测效果达到最优。
图5是接收者操作特征(receiver operating characteristic,ROC) 曲线,可以看出黑色和蓝色的曲线明显低于绿色和红色曲线,表明被试1和被试5的预测效果差,被试2和被试3的预测效果好,这与对表1的分析结果一致。

图5 ROC曲线图Fig.5 ROC curve graph
本文算法与文献[2,17-20]的癫痫预测方法效果对比如表2。文献[2]使用皮尔逊相关系数作为特征,然后利用卷积神经网络进行预测,其预测的准确率为89.98%,而本文算法的准确率为91.26%,高于文献[2]的准确率,表明时空特征能提高癫痫发作预测的准确率。从表2可知,文献[17]的癫痫发作预测方法的准确率很高,但该文献研究单导联脑电癫痫发作预测,通常需要使用癫痫灶区的脑电信号,其隐含的癫痫信息要求较高,为了获得灶区的单通道脑电信号,需要提前对脑电信号进行筛选。文献[20]预测的准确率很高,同时误报率也较高,较高的误报率会引起患者紧张,不利于癫痫的治疗。通过对比可知,本文方法在预测精度方面还有待提高,算法还需优化,这也是本文需要进一步改进的地方。
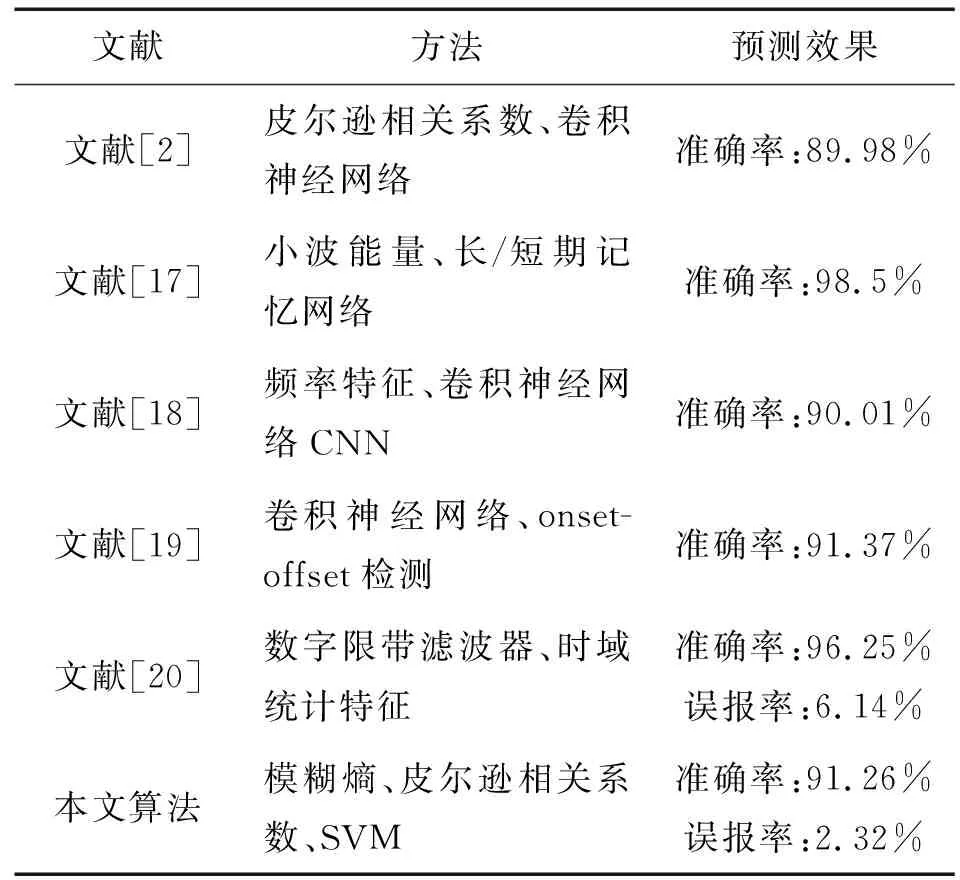
表2 现有癫痫预测方法的性能比较Tab.2 Performance comparison of existing methods for seizure prediction
4 结束语
本文提出的基于SVM分类器的癫痫脑电时空特征提取方法,与单一特征预测癫痫发作算法相比,具有较高的准确率和较低的误报率,可以为患者提供及时有效的预警,缓解患者的心理压力。因此,本文方法提取的癫痫时空特征信息能较好地实现癫痫发作预测,未来可以用于癫痫患者的临床预警。

