基于几何精确梁的风力机叶片动力学建模及动态特性分析*
谢 浩,李德源,曲珍壮,黄 维
基于几何精确梁的风力机叶片动力学建模及动态特性分析*
谢 浩,李德源†,曲珍壮,黄 维
(广东工业大学 机电工程学院,广州 510006)
基于几何精确梁理论,结合广义-时间预测法的迭代算法,考虑叶片复合铺层材料的各向异性特性,建立了大型风力机叶片的几何非线性动力学模型并导出了相应的特征方程,编制了数值仿真程序。通过对几何非线性梁标准算例和某10 MW柔性风力机叶片动力特性的模拟分析,验证了动力学模型的正确性,以及几何精确梁模型对分析叶片几何非线性大变形及其所导致的非线性动力学效应的有效性。叶片在静止和转动工况下的模态分析结果表明,在动力刚化效应作用下,叶片的固有频率会随着转速的增加而增大,动力刚化效应在挥舞方向比在摆振方向更明显,在低阶模态比在高阶模态更明显。
风力机叶片;几何精确梁;动力刚化;模态分析
0 引 言
随着全球能源危机与环境污染等问题的日益加剧,以风能为代表的各种清洁可再生能源逐渐被世界各地所重视。为了提高风力机的风能利用率、降低发电成本,风力机叶片尺寸的大型化已经成为风力机的重要发展方向[1]。
风力机叶片具有细长结构的特点,在研究分析叶片结构时,叶片通常被近似假设为梁模型来进行研究。在工程上,叶片梁模型的分析常使用基于小变形假设的软件,如Bladed、HAWC2等[2-3]。对于短叶片,小变形假设能获得较为准确的结果和较高的计算效率。然而随着风力机的大型化,小变形假设已经难以表达更为细长的柔性叶片大变形所带来的几何非线性现象[4]。对大变形叶片的几何非线性问题研究已经成为风力机领域的重点研究方向之一[5]。
现在常用的非线性梁模型主要有多体动力学模型[6]、绝对节点坐标模型[7]以及几何精确梁模型[8-10]。几何精确梁模型能以较少的节点自由度获得较高的计算精度,能准确地用于叶片的非线性动力学分析[11],采用线性化系统得到的解析形式的模态便于获得系统的低自由度的非线性模态振动方程,为大型柔性叶片的非线性振动研究提供了有效途径。
本文基于几何精确梁理论,使用四元数表达截面转动,采用Gauss-Lobatto积分法则,结合具有二阶精度的广义-时间预测法[12]迭代算法,考虑叶片复合铺层材料的各向异性特性,建立大型风力机叶片的非线性动力学模型,并对该模型进行线性化求解。通过与丹麦技术大学(Technical University of Denmark, DTU)所提供的10 MW风力机叶片数据[13]作对比,对叶片动力学模型的正确性进行验证,研究几何精确梁模型对分析非线性大变形和动力学特性的可行性,为大型风力机叶片的结构分析及后续的气弹耦合分析提供一个计算效率高且准确的非线性动力学模型。
1 风力机叶片非线性单元模型
1.1 叶片构型及变形
风力机叶片是由一定几何形状的翼型与多种材料铺层所形成的,由于截面形状较为特殊,且复合材料铺层的各向异性同一截面的铺层厚度不一,因此具有重心、剪心、扭心不共点的特性和材料的各向异性特性。图1为10 MW风力机叶片的主要截面形状。
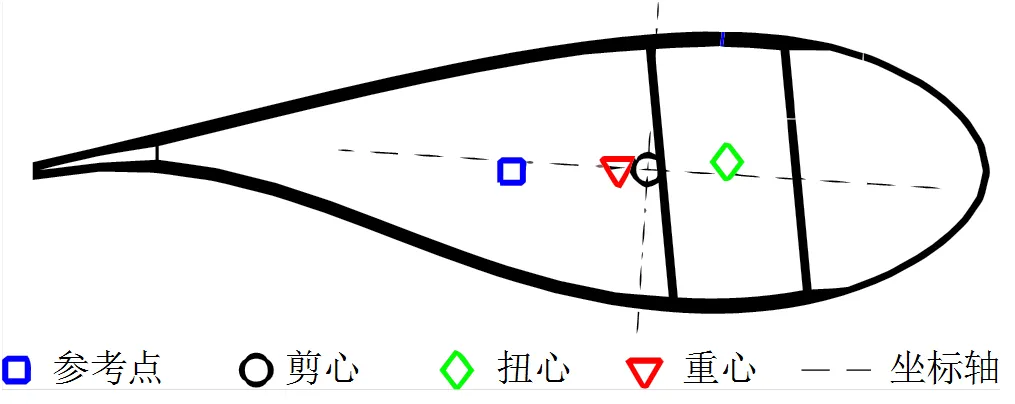
图1 风力机叶片截面
在叶片根部建立全局坐标系(G,G,G),G与风轮平面垂直,G与叶根平面垂直。以各截面的剪心作为原点建立各截面的局部弹性坐标系(E,E,E),三个坐标轴的指向与全局坐标系一致,定义此时的叶片状态为直叶片的参考构型。
将各截面的剪心连成一线,该连线则为叶片的轴线。基于几何精确梁的平截面假设,叶片的变形和叶片的预弯预扭初始构型,可视作是由各截面EE平面上的平移与绕E轴的转动所形成的。
1.2 截面转动描述
几何精确梁理论基于由Timoshenko梁理论发展而成的Reissner梁理论[14],同样采用平截面假设,即梁的位移形变由梁轴线位移与截面转动所形成,还使用三维有限转动理论,精确得到梁在大位移大变形条件下的应变−位形关系,如图2所示。

图2 截面转动在梁变形前后的变化关系
图2中,(1,2,3)为全局坐标系的基向量,当梁发生变形后,同一截面的局部坐标系基向量(0)变成了(1),其中的转动变化可通过三阶方向余弦矩阵来表示
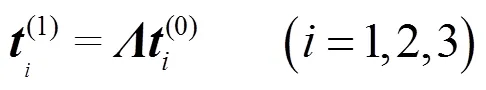
方向余弦矩阵有9个分量,计算效率低,截面转动的更新也比较复杂,欧拉四元数是空间三维转动非奇异的最少参数表达,因此本文采用欧拉四元数描述截面的转动[15]。四元数与方向余弦矩阵的关系为

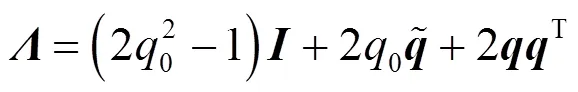

由欧拉四元数性质可知,0可通过计算所得,则可以用节点线位移、节点欧拉参数,定义节点的位移向量为
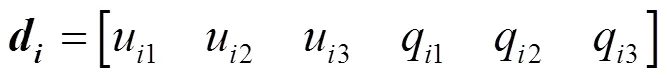
通过四元数法与增量转动法得到增量四元数可实现旋转的可加性,用于确定截面转动。四元数增量可以使用指数映射的方式
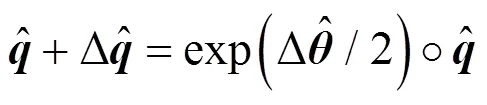

节点的角速度和角加速度与四元数的关系为


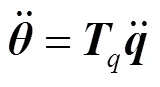
对于10 MW叶片截面节点的选择,本文采用Legendre-Gauss-Lobatto积分法则中的积分点。
1.3 动力学平衡方程
几何精确梁理论采用一阶假设的Reissner应变,定义Reissner应变为平动应变向量,应变为转动应变向量,则截面等效力、与应变、的关系,即本构关系为


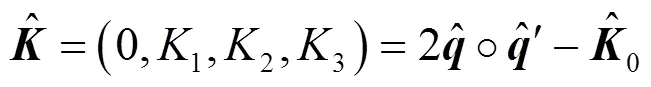

根据DTU所提供的10 MW风力机叶片数据,建立叶片三维模型,再根据Lobatto积分点选择相应叶片截面,提取对应叶片截面的有限元单元几何数据,加上叶片铺层材料的数据,导入专业分析截面软件VABS计算得到叶片截面刚度矩阵[16]。
结合虚功原理,得到叶片单元的内力、外力和惯性力的虚功平衡方程为
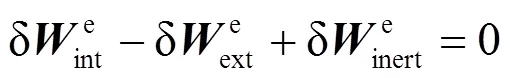
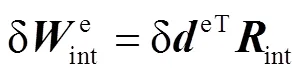

1.4 平衡方程的线性化

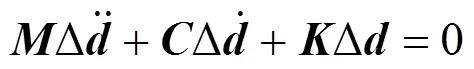

当叶片从静止加速到所设定的转速且方程达到平衡状态时,在平衡位置处线性化质量矩阵及刚度矩阵,由特征值分解计算转动叶片的模态的公式如下
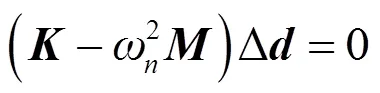
1.5 稳态位置求解
叶片非线性系统动力学平衡方程的求解需要使用具有预测−校正特性的方法,此处采用广义-时间预测法[12]。
广义-时间预测−校正的方法对增量平衡方程的求解为



由位移增量得到速度和加速度增量为:

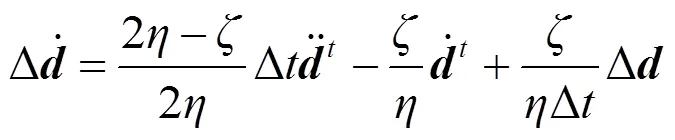
2 算例验证
本节根据以上几何精确梁理论公式,编写对应的MATLAB程序,构建几何精确梁模型,并用以下三个算例验证几何精确梁理论对静力学及动力学特性描述的准确性。
2.1 纯弯曲梁
为了体现几何精确梁理论描述非线性大变形的准确性,以纯弯曲悬臂梁的静力学变形作为算例。根据纯弯理论可得,梁仅在自由端受到一定弯矩后,梁轴线会变形成一段圆弧,其对应曲率为(),为弯矩,为梁截面刚度。现对梁长1 m的悬臂梁自由端施加的弯矩,则得到变形后梁轴线的曲率解析值为。
图3为几何精确梁理论分析不同的所对应的弯矩对悬臂梁变形的结果,与相应的解析值作为对比,两者结果基本符合。

图3 纯弯曲梁变形
2.2 叶片静挠度
为了体现几何精确梁理论能对结构不规则且具有复合材料铺层的10 MW风力机叶片进行准确的变形描述,对叶片末端分别在挥舞(垂直于风轮平面的方向)、摆振方向(风轮平面所在的方向)施加−100 000 N的力,利用几何精确梁理论计算其静挠度,并与使用软件Abaqus的计算结果做对比,分别如图4所示,两者结果基本符合。
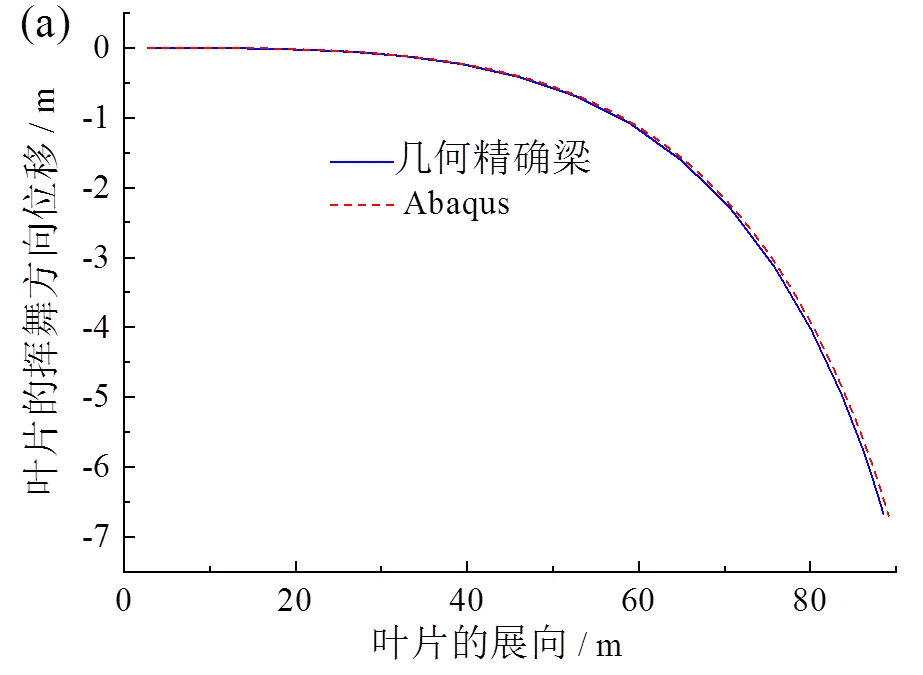
2.3 旋转梁的动力特性
为了体现几何精确梁理论对旋转物体动力学特性的准确性,以定轴旋转梁为研究对象,此矩形截面梁的几何尺寸比例与叶片的尺寸比例相近,长度= 7 m,横截面宽= 0.5 m、高= 0.15 m,材料为叶片结构常用的环氧树脂,弹性模量= 4.0 GPa,剪切模量= 1.481 4 GPa,密度= 1 140 kg/m3,泊松比= 0.35。
表1为使用几何精确梁模型,结合21个Lobatto积分点,计算该定轴旋转梁分别在0 r/min、10 r/min、20 r/min转速下的前五阶固有频率结果,以及使用软件ANSYS Workbench对该梁做有限元分析的结果,该有限元模型采用的是Beam188梁单元,该梁单元考虑了剪切效应,每个节点有3个平动自由度,3个转动自由度,共6个自由度。算例单元数为234个。

表1 旋转梁的固有频率对比
表1的对比结果表明了几何精确梁模型可以用较少的自由度得出旋转梁的高精度动力学特性。
3 叶片的模态分析
上一节已证明几何精确梁理论对描述复合材料非线性大变形及动力学特性表达的准确性,现使用几何精确梁理论,同样基于21个Lobatto积分点,对静止的风力机叶片进行模态分析,研究对象采用DTU所提供的10 MW风力机叶片,得到各阶模态相应固有频率如表2所示,相应振型如图5所示。

表2 静止叶片的模态分析结果

图5 静止叶片的前六阶振型
进一步通过几何精确梁理论对风力机叶片分别在转速为3.0 r/min、6.0 r/min、9.6 r/min(额定工况转速)、15.0 r/min、19.2 r/min时进行模态分析,得到各转速对应的各阶模态固有频率如表3所示,对应变化趋势如图6所示。

表3 旋转叶片的固有频率对比

图6 旋转叶片的固有频率对比
动力刚化效应是指物体在转动过程中自身的固有频率随着转速的增加而升高。由表3和图6可得,随着叶片转速的增大,叶片的固有频率越来越高,动力刚化效应变得更加明显。当叶片从静止加速到额定工况转速9.6 r/min时,前六阶固有频率的增量分别为6.14%、2.12%、2.21%、0.76%、1.04%、0.44%,而加速到两倍额定工况转速19.2 r/min时,增量分别为22.16%、8.09%、8.49%、2.98%、4.04%、1.70%。由此可见,叶片的挥舞方向的动力刚化效应比摆振方向更加明显,且动力刚化效应对一阶挥舞及一阶摆振的影响比对高阶振型的影响更加大。
4 结 论
基于几何精确梁理论,结合广义-时间预测法,建立梁的几何非线性动力学模型,并通过不同的算例验证了该模型对描述非线性大变形及动力学特性的准确性。然后在此模型的基础上,加入10 MW风力机的数据,考虑叶片复合铺层材料的各向异性特性,建立大型风力机叶片的非线性动力学模型,将叶片非线性动力学模型线性化,对各转速的叶片进行模态分析。通过基于几何精确梁理论对大型风力机叶片的建模及动力学特性分析可得出以下结论:
(1)所建的几何精确梁模型能对柔性梁进行准确的动力学分析。
(2)模型考虑叶片复合铺层材料的各向异性特性,能对大型风力机叶片进行准确的模态分析。
(3)大型风力机叶片随着转速的增大,其动力刚化效应越明显,挥舞方向的动力刚化效应比摆振方向更明显,低阶振型动力刚化效应比高阶振型更明显。
(4)几何精确梁模型能够对大型风力机叶片做非线性大变形及动力学特性分析,且能以较少的自由度对叶片进行计算效率高且准确的动力学特性分析,为叶片非线性振动和气弹耦合响应的研究提供了可行方案。
[1] 乐威. 新能源背景下我国风力发电现状和未来发展方向探索[J]. 绿色环保建材, 2020(11): 165-166. DOI: 10.16767/j.cnki.10-1213/tu.2020.011.080.
[2] 赵俊杰. 2MW风力发电机叶片设计与分析[D]. 邯郸: 河北工程大学, 2018.
[3] PASSON P, KÜHN M, BUTTERFIELD S, et al. OC3—benchmark exercise of aero-elastic offshore wind turbine codes[J]. Journal of physics: conference series, 2007, 75: 012071. DOI: 10.1088/1742-6596/75/1/012071.
[4] 黄俊东, 夏鸿建, 李德源, 等. 大型风力机柔性叶片非线性气弹模态分析[J]. 机械工程学报, 2020, 56(14): 180-187. DOI: 10.3901/JME.2020.14.180.
[5] HANSEN M O L, SØRENSEN J N, VOUTSINAS S, et al. State of the art in wind turbine aerodynamics and aeroelasticity[J]. Progress in aerospace sciences, 2006, 42(4): 285-330. DOI: 10.1016/j.paerosci.2006.10.002.
[6] 莫文威. 基于多体模型的水平轴风力机气弹耦合分析[D]. 广州: 广东工业大学, 2013.
[7] 张海波. 绝对节点坐标法在大型风力机叶片结构分析中的应用研究[D]. 广州: 广东工业大学, 2021. DOI: 10.27029/d.cnki.ggdgu.2021.000773.
[8] 肖乃佳. 基于几何精确梁理论的框架的弱形式求积元分析[D]. 北京: 清华大学, 2011.
[9] 吕品, 廖明夫, 尹尧杰. 考虑几何非线性的风力机叶片气弹模型[J]. 机械科学与技术, 2015, 34(12): 1805-1812. DOI: 10.13433/j.cnki.1003-8728.2015.1201.
[10] REISSNER E. On one-dimensional large-displacement finite-strain beam theory[J]. Studies in applied mathematics, 1973, 52(2): 87-95. DOI: 10.1002/sapm197352287.
[11] ROMERO I. A comparison of finite elements for nonlinear beams: the absolute nodal coordinate and geometrically exact formulations[J]. Multibody system dynamics, 2008, 20(1): 51-68. DOI: 10.1007/s11044-008-9105-7.
[12] 黄正. 基于等几何配点法的几何精确Euler-Bernoulli梁几何非线性分析[D]. 武汉: 华中科技大学, 2017. DOI: 10.7666/d.D01313662.
[13] BAK C, ZAHLE F, BITSCHE R, et al. The DTU 10-MW reference wind turbine[R]. Fredericia: DTU, 2013.
[14] SHABANA A A, YAKOUB R Y. Three dimensional absolute nodal coordinate formulation for beam elements: theory[J]. Journal of mechanical design, 2001, 123(4): 606-613. DOI: 10.1115/1.1410100.
[15] ZUPAN E, SAJE M, ZUPAN D. The quaternion-based three-dimensional beam theory[J]. Computer methods in applied mechanics and engineering, 2009, 198(49/52): 3944-3956. DOI: 10.1016/j.cma.2009.09.002.
[16] YU W B, HODGES D H, HO J C. Variational asymptotic beam sectional analysis-An updated version[J]. International journal of engineering science, 2012, 59: 40-64. DOI: 10.1016/j.ijengsci.2012.03.006.
Wind Turbine Blade Dynamics Modeling and Dynamic Characteristics Analysis Based on Geometrically Exact Beam Theory
XIE Hao, LI De-yuan, QU Zhen-zhuang, HUANG Wei
(School of Electromechanical Engineering, Guangdong University of Technology, Guangzhou 510006, China)
Based on the geometrically exact beam theory, combined with the iterative algorithm of generalized-time prediction method, the geometric nonlinear dynamics model of large wind turbine blade was established considering the anisotropic characteristics of composite laminates. The corresponding characteristic equations were derived and a numerical simulation program was developed. The correctness of the dynamic model and the effectiveness of the geometrically exact beam model in analyzing the large deformation of the geometrically nonlinear blade and its nonlinear dynamic effects were verified by the simulation analysis of the standard geometric nonlinear beam model and the dynamic characteristics of a 10 MW flexible wind turbine blade. The results of the modal analysis of the blade at rest and rotation conditions showed that the natural frequency of the blade increased with the increase of the rotational speed under the dynamic stiffening effect, and the dynamic stiffening effect was more obvious in flapwise direction than in edgewise direction, and more obvious in the low order modal than in the high order modal.
wind turbine blade; geometrically exact beam; dynamic stiffening; modal analysis
2095-560X(2022)03-0203-06
TK83;O313.7
A
10.3969/j.issn.2095-560X.2022.03.003
2022-03-11
2022-04-06
李德源,E-mail:lidey@gdut.edu.cn
谢 浩(1997-),男,硕士研究生,主要从事基于几何精确梁模型的风力机叶片研究。
李德源(1965-),男,教授,硕士生导师,主要从事大型风力机气动与结构分析、风力机系统测试和计算机软件的开发与应用等方面的研究。

