一种改进的GSC自适应波束形成的语音增强方法
常雅婷 于玲


摘要:传统的广义旁瓣抵消(Generalized Sidelobe Canceller,GSC)算法中,由于主通道采用的算法是固定波束形成(Fixed Beamformer,FBF)算法,其权值不随语音信号的改变而变化,导致算法适应性较差,因此,干扰和噪声在固定波束形成类算法中抑制效果不明显。针对这一问题,该文将传统的GSC算法中主通道的固定波束形成模块改为自适应LCMV波束形成模块,并引入对角载入量的控制,通过调整对角载入量,使其可以自适应输出最优权值,有效地抑制干扰和噪声。得到的剩余带噪语音信号经过辅助通道的阻塞矩阵和自适应噪声抵消模块进行噪声的二次估计,从而得到目标语音;再针对非相干噪声,采用维纳后置滤波算法进行降噪处理,通过这两步处理,获得更具鲁棒性的GSC-LCMV自适应波束形成算法。仿真结果表明,该文算法对噪声和干扰的抑制效果更优,波束图可以形成更低的旁瓣,输出具有更高信噪比的语音信号。
关键词:语音增强;麦克风阵列;自适应波束形成;对角载入量;维纳滤波
中图分类号:TP18 文献标识码:A
文章编号:1009-3044(2022)15-0068-04
近年来,语音增强方法[1-2]在语音交互中具有十分重要的角色。语音增强技术分为三大类[3-5],其中,多通道语音增强利用麦克风阵列[6-8]获取空域信息,再利用自适应滤波或波束形成[9-11]等算法对语音信号进行处理,抑制噪声和干扰,从而达到增强目标语音信号的目的。波束形成准则使其在理想方向形成一个增益最大的波束。自适应波束形成算法因可以根据语音信号的变化而自适应更新权值,更受学者们青睐。自适应波束形成算法的两个典型原型为线性约束波束形成(LCMV)算法和广义旁瓣相消(GSC)算法[12]。其中GSC结构主要由固定波束形成模块,阻塞矩阵模块以及噪声抵消模块构成。
在噪声抵消模块中,最小均方算法方法简单,便于实现,最为常见。但由于其稳态误差与收敛速度相互影响,算法的性能有待提高;固定波束形成中固定不变的权值对噪声和干扰抑制能力不足。针对以上问题,本文将固定波束形成模块改为自适应的LCMV波束形成模块,引入对角载入量,提出GSC-LCMV波束形成算法;在辅助通道的噪声抵消模块中采用新的变步长lms算法。仿真结果表明,本文算法可以有效抑制噪声和干扰信号,波束图中形成更低的旁瓣,输出更高的语音信噪比,提高后续基于语音的应用效果。
1麦克风阵列语音信号模型
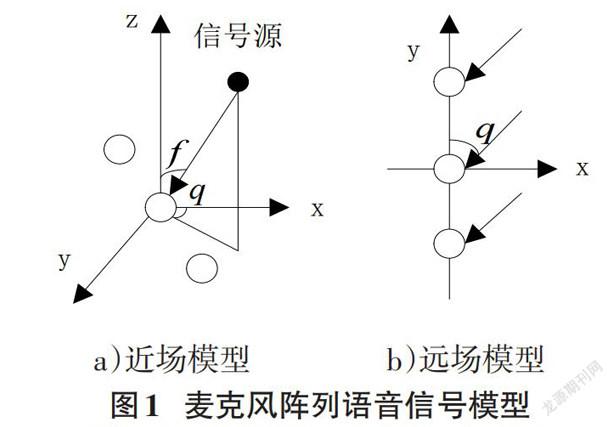
麦克风阵列的语音信号处理中,首先要明确语音信号为何种模型。其判断准则为:
[L>2d2λ,符合远场模型L≤2d2λ,符合近场模型] (1)
其中[L]为声源到参考阵元的中心点距离,[d]为阵列的总间距,[λmin]为当前语音波长。图1为麦克风阵列语音信号的远场模型与近场模型。
在a)近场模型中,语音信号被看作球面波入射,计算过程中需要计算各麦克风之间的信号幅度差问题。
在b)远场模型中,语音信号的传播看作平面波信号,信号传播过程中产生的幅度衰减可以忽略不计,只需考虑每个麦克风间的时延差值。
对于2N+l个麦克风构成的均匀直线麦克风阵列,语音信号的入射方向与y轴的夹角为[θ],两个相邻麦克风间的距离为D,时延为零的参考麦克风为阵列最中心的麦克风,则第n个麦克风的时延为:
[τn=nDcos(θ)c,n∈0,1,2,3...] (2)
2 自適应波束形成语音增强算法
2.1 传统的广义旁瓣抵消算法
传统的广义旁瓣抵消算法主要由三个模块组成:固定波束成形模块,阻塞矩阵模块和噪声抵消模块。
如图2所示为传统的GSC算法结构图,假设信号的入射角为[θ],麦克风数量为[N],固定波束形成主要采用延迟相加波束形成算法(DSB),主通道采用的算法为固定波束成形算法,权值不因语音信号的变化而自适应改变,但对于语音信号的到达方向的估计,影响着语音信号的增强方向,若目标语音信号进入阻塞矩阵中,则形成语音失真。因此,传统的GSC算法并不完善,对于噪声的抑制效果也不理想。
2.2 LCMV自适应波束形成算法
线性约束最小方差(LCMV)波束形成器的约束方程表达式为:
[Wopt=argminwWHRxW] (3)
[s.t.WHC=f] (4)
其中:C——约束矩阵;f——约束矢量。
假设[x1(n),x1(n),…,xN-1(n)]是阵列的采样快拍,则信号的联合概率密度表达式为:
[p(x1(n)…xN-1(n))=n=1Nexp[-xH(n)R-1xx(n)]πdet(Rx)] (5)
对于协方差矩阵的最大似然估计的求解,第一步对联合概率密度函数取对数,第二步求矩阵梯度,又称为采样协方差矩阵:
[Rx=1Kn=1Kx(n)xH(n)] (6)
利用拉格朗日算法解得最优权矢量:
[wLCMV=RxC[CHRxC]-1f] (7)
若信号为统计独立同分布的高斯白信号:
[wq=C[CHRxC]-1f] (8)
经过LCMV波束形成器输出的语音信号:
[b(n)=wqx(n)] (9)
2.3改进的GSC-LCMV波束形成器
Tian等利用 RLS 算法在高斯噪声下实现了二次不等式约束的 LCMP 波束形成[13]。受文献[13]的启发,为提高算法的抗干扰能力和降噪能力,本文将LCMV最优波束形成器通过GSC结构实现,采用LCMV波束形成器代替传统GSC结构中的固定波束形成器,同时引入对角载入量,将合适的正数添加在协方差矩阵的对角线上,以得到较小的特征值分散程度,对LCMV波束形成器的权值进行二次约束,输出最优权值,同时降低波束形成的旁瓣。图3为改进的GSC-LCMV波束形成结构图。
如图3所示,假设[θ]为信号的入射角度,阵列由[N]个阵元组成,[[x0(n),x1(n),...xN-1(n)]]为阵列接收到的信号,信号首先通过时延估计计算出每个麦克风的时延,接下来,通过时延补偿将信号对齐;信号经过主通道的自适应LCMV波束形成器求得可以自适应更新的最优权矢量:
[wq=C[CHRxC]-1f] (10)
加入对角载入量,得到较小特征值的分散程度,降低波束形成的旁瓣,得到新的表达式:
[wq=C[CH(Rx+λI)C]-1f] (11)
[wHqwq=CHfH[CH(Rx+λI)C]-2f] (12)
关于[λ] 求导:
[ddλwHqwq=-2CHfH[CH(Rx+λI)C]-2f] (13)
因此[ddλwHqwq<0],[wHqwq]关于对角载入量是单调递减,此时随着对角载入量[λI]的改變,[wq]的模值发生改变,使得自适应权值满足二次约束,通过调整对角载入量可以得到最优权矢量。
主通道得到语音的参考信号表达式为:
[ys(n)=wq⋅x(n)] (14)
下通道阻塞矩阵B表达式:
[B=1-10…01-1⋱⋮⋱⋱⋱0…010⋮0-1] (15)
则经过阻塞矩阵处理后的信号为:
[z(n)=BH⋅x(n)] (16)
经过阻塞矩阵输出的信号[z(n)]只包含噪声信息,进入噪声抵消部分[14]的自适应滤波器过滤掉阻塞矩阵中的目标语音,对于滤波器系数的求解,使用一种新的变步长LMS算法[15]进行迭代求解。其具体如下:
[y(n)=WT(n)X(n)e(n)=d(n)-y(n)=d(n)-WT(n)X(n)α(n)=e(n)e(n-1)2β(n)=λβ(n-1)+(1-λ)Δe(n)μ(n)=β(n)1+e-α(n)e(n)-0.5 W(n+1)=W(n)+μX(n)e(n) ] (17)
式(17)中,[μ]是迭代步长,[X(n)]是输入的信号,[e(n)]是误差信号,由期望信号与输出信号相减得到,[W(n)]为当前时刻下滤波器的权系数,[W(n+1)]是下一时刻滤波器的权系数。
经自适应滤波器得到的噪声信号表达式:
[y1(n)=W(n+1)*μ(n)] (18)
改进后的算法主通道LCMV波束形成器输出的信号与噪声抵消部分得到的噪声估计作差,最终得到目标语音信号:
[y(n)=ys(n)-y1(n)] (19)
2.4后置维纳滤波算法
GSC算法对于非相干噪声的处理效果有限,将GSC算法与维纳滤波器结合起来,针对非相干噪声的处理本文采用维纳滤波器:
[W(ω)=2N(N-1)Rei=1N-1j=i+1Nϕxixj(ω)1Mi=1Nϕxi(ω)] (20)
式中:[ϕxixj]——表示第[i]个阵元和第[j]个阵元接收到的信息的互功率谱;[ϕxi]——第i个阵元接收到的信息的自功率谱;[N]——阵元个数。
互功率谱与自功率谱的求解表达式为:
[φxixj(ω)=FFT(xi(n),N)FFT∗(xi(n),N)2/N] (21)
[φxi(ω)=FFT(xi(n),N)2/N] (22)
式中:[FFT(xi(n),N)]——对第[i]个麦克风的数据作N点FFT运算;*——共轭运算符。
相关系数由求解Wiener-Hopf方程得到:
[n∈lw(n)Rxx(l-n)=Rss(n),l∈I] (23)
式中[Rxx(n)]——阵列接收信号的自相关函数;[Rss(n)]——语音信号在阵列接受信号中的自相关函数。
3算法仿真与分析
为验证本文算法的语音增强性能,本文选取均匀直线分布的麦克风构成麦克风阵列。麦克风个数N为8,相邻麦克风间距D为0.5m,语音信号的入射方向为[40∘],干扰信号方向为[-40∘],干噪比30db,语音信号的采样频率8kHz。
如图4为原始语音信号波形图:
将5dB的信噪比和零均值的高斯白噪声加入原始语音信号中后,得到带噪语音信号波形图,如图5所示。
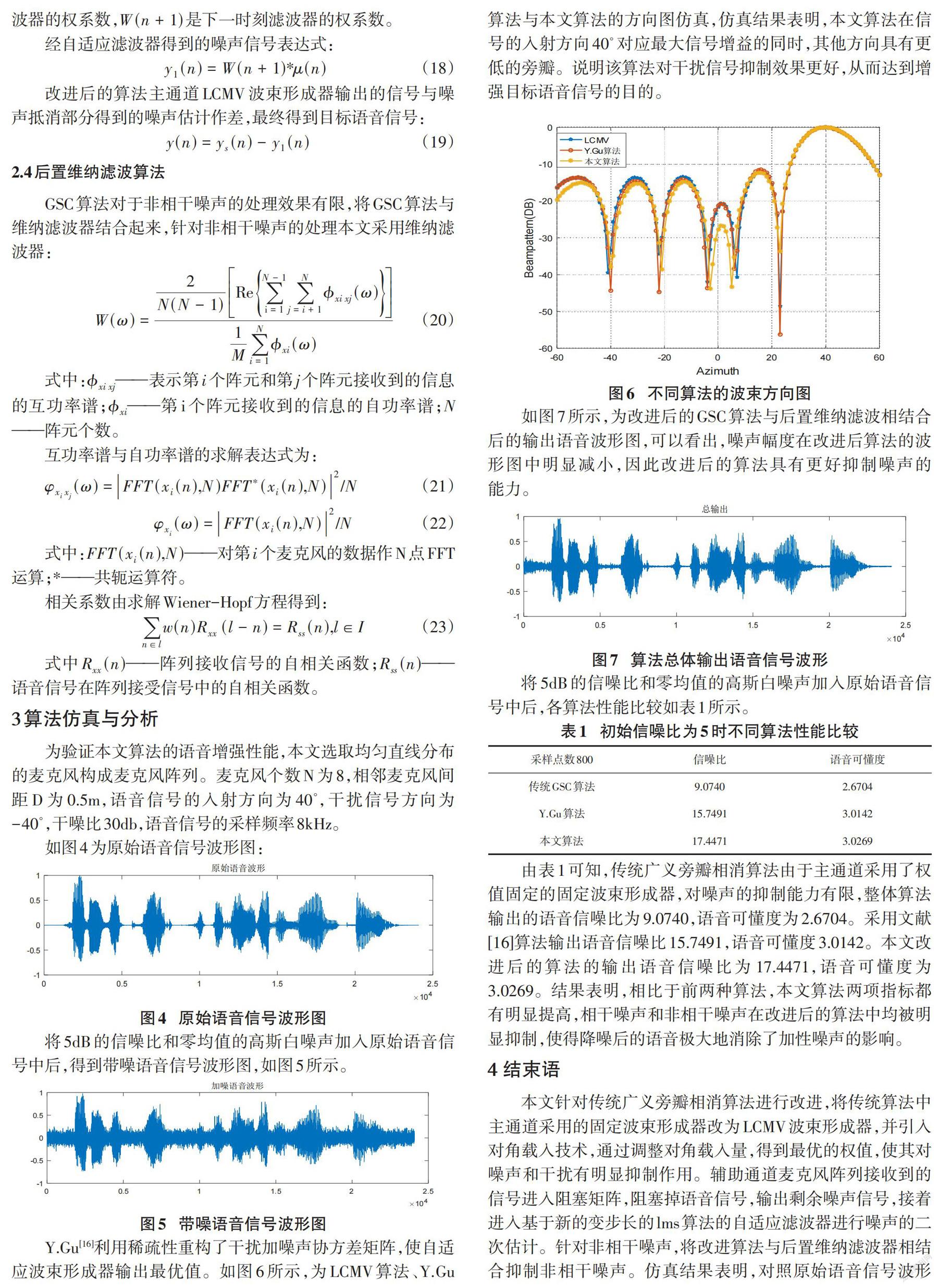
Y.Gu[16]利用稀疏性重构了干扰加噪声协方差矩阵,使自适应波束形成器输出最优值。如图6所示,为LCMV算法、Y.Gu算法与本文算法的方向图仿真,仿真结果表明,本文算法在信号的入射方向[40∘]对应最大信号增益的同时,其他方向具有更低的旁瓣。说明该算法对干扰信号抑制效果更好,从而达到增强目标语音信号的目的。
如图7所示,为改进后的GSC算法与后置维纳滤波相结合后的输出语音波形图,可以看出,噪声幅度在改进后算法的波形图中明显减小,因此改进后的算法具有更好抑制噪声的能力。
将5dB的信噪比和零均值的高斯白噪声加入原始语音信号中后,各算法性能比较如表1所示。
由表1可知,传统广义旁瓣相消算法由于主通道采用了权值固定的固定波束形成器,对噪声的抑制能力有限,整体算法输出的语音信噪比为9.0740,语音可懂度为2.6704。采用文献[16]算法输出语音信噪比15.7491,语音可懂度3.0142。本文改进后的算法的输出语音信噪比为17.4471,语音可懂度为3.0269。结果表明,相比于前两种算法,本文算法两项指标都有明显提高,相干噪声和非相干噪声在改进后的算法中均被明显抑制,使得降噪后的语音极大地消除了加性噪声的影响。
4 结束语
本文针对传统广义旁瓣相消算法进行改进,将传统算法中主通道采用的固定波束形成器改为LCMV波束形成器,并引入对角载入技术,通过调整对角载入量,得到最优的权值,使其对噪声和干扰有明显抑制作用。辅助通道麦克风阵列接收到的信号进入阻塞矩阵,阻塞掉语音信号,输出剩余噪声信号,接着进入基于新的变步长的lms算法的自适应滤波器进行噪声的二次估计。针对非相干噪声,将改进算法与后置维納滤波器相结合抑制非相干噪声。仿真结果表明,对照原始语音信号波形图,本文改进后的算法语音波形图与其基本保持一致,输出的语音信噪比也有明显提高。证明改进后的算法具有更好地抑制噪的能力,为语音增强算法提供了新的思想。
参考文献:
[1] Griffiths L,Jim C.An alternative approach to linearly constrained adaptive beamforming[J].IEEE Transactions on Antennas and Propagation,1982,30(1):27-34.
[2] Ali R,van Waterschoot T,Moonen M.Correction to:an integrated MVDR beamformer for speech enhancement using a local microphone array and external microphones[J].EURASIP Journal on Audio,Speech,and Music Processing,2021,2021:15.
[3] Sun J Y,Sun C L,Hong Y.A new speech enhancement method based on nonnegative low-rank and sparse decomposition[J].Journal of Physics:Conference Series,2021,1848(1):012090.
[4] Kammi S.Single channel speech enhancement using an MVDR filter in the frequency domain[J].International Journal of Speech Technology,2019,22(2):383-389.
[5] Wang X F,Guo Y M,Fu Q,et al.Speech enhancement using multi-channel post-filtering with modified signal presence probability in reverberant environment[J].Chinese Journal of Electronics,2016,25(3):512-519.
[6] Nossier S A,Wall J,Moniri M,et al.An experimental analysis of deep learning architectures for supervised speech enhancement[J].Electronics,2020,10(1):17.
[7] 续娇.基于自适应波束成形的语音增强算法研究与实现[D].北京:北京交通大学,2019.
[8] 王兆阳.基于波束形成算法的麦克风阵列语音处理研究与实现[D].哈尔滨:哈尔滨工业大学,2015.
[9] 郑毅豪.基于差分麦克风阵列的波束形成技术研究[D].武汉:湖北工业大学,2020.
[10] 闫姝,权建军.基于麦克风阵列的语音增强算法研究[J].自动化仪表,2019,40(9):59-62.
[11] 张蒙.室内环境下基于麦克风阵列的语音增强算法研究[D].深圳:深圳大学,2016.
[12] 李连,李铌.基于麦克风阵列的嘈杂环境下的鲁棒语音增强算法[J].电子制作,2020(15):51-53,46.
[13] Tian Z,Bell K L,van Trees H L.A recursive least squares implementation for LCMP beamforming under quadratic constraint[J].IEEE Transactions on Signal Processing,2001,49(6):1138-1145.
[14] Wang R G,Wang Y X,Han C,et al.Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation[J].2021 IEEE International Conference on Signal Processing,Communications and Computing (ICSPCC),2021:1-5.
[15] 景源,汪洪涛.一种新的变步长LMS算法及在自适应波束形成中的应用[J].辽宁大学学报(自然科学版),2018,45(4):326-330.
[16] Gu Y J,Leshem A.Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation[J].IEEE Transactions on Signal Processing,2012,60(7):3881-3885.
【通聯编辑:唐一东】

