CIPP视域下基于组合赋权法的创新创业教育评价研究

王 静， 王美骄， 张 妍

(1.辽宁师范大学 数学学院，辽宁 大连 116029；2.辽宁师范大学 外国语学院，辽宁 大连 116029)

自国家明确提出开展创新创业教育以来，我国高校的创新创业教育己经走过了10多年的历程.尽管我国高校创新创业教育已经取得了众多研究成果，但与创新创业教育先行者的西方国家相比，我国对创新创业教育体系的构建和评价尚未成熟，仍处于探索阶段.

众多学者对高校创新创业教育评价体系展开了相关研究.谭晋钰分别从教学体系、制度保障、文化氛围和组织运行以及评价反馈四个角度，提出构建高校创新创业教育评价体系[1].徐英等从政府、学校、学生、社会四个维度构建了“四位一体”的创新创业教育评价指标体系[2].周燕等认为，创新型人才培养是高校创新创业教育的主要任务，高校应从教育政策、课程体系、教育平台和师资队伍等方面构建创新创业教育评价体系[3].周风等从教育背景、教育投入、教育过程、教育成果4个方面分别建立了高校创新创业教育评价体系的各层级指标，利用层次分析法给各层级指标赋予相关比例权重[4].

在文献[4]中，作者使用层次分析法对评价体系中各层次指标赋权.层次分析法属于主观赋权法，其优势在于缺少样本数据的情况下仅凭主观经验即可赋权，缺点在于该方法完全依赖主观性，从而可信度受到影响.本文采用CIPP准则建立高校创新创业教育评价体系中的各层次指标因素，然后通过组合赋权法计算确定各层级指标权重，将层次分析法的经验优势和熵值法的客观质量优势相结合，进而构建相对合理的创新创业评价指标体系.

1 创新创业教育评价指标体系构建

高校创新创业教育培养是一个“全员、全过程、全视角”的“三全育人”生态系统.而创新创业教育评价则是针对创新创业教育改革所进行的“全口径、全流程、全视角”的“三全育人”质量评价.因此，高校创新创业教育评价体系属复杂系统，选择评价指标时应遵循全面性、科学性、可操作性、动态性原则.CIPP评价原则主要从背景评价、输入评价、过程评价和成果评价等不同视角出发，不仅着重于终结性评价，最可贵的是将过程性、形成性、诊断性评价有机结合，突出教育评价的持续改进作用.CIPP 教育评价准则4个环节的内涵和意义参见文献[5].根据CIPP评价原则, 选择四大类14个子项指标，如表1所示.

表1 创新创业教育评价指标体系

2 指标权重的确定

2.1 权重判断矩阵

首先，根据各个指标之间的重要性关系建立权重判断矩阵.权重判断矩阵是指对于上一层次因素，本层次各因素之间相对重要性的比较.设目标层为A，准则层的各因素为U={U1,U2,U3,U4}，确定每两个因素之间对A的影响程度，用aij表示Ui与Uj对A的影响之比：

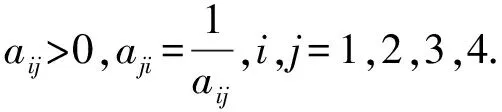
设B=(aij)为权重判断矩阵，赋值主要通过咨询相关专家的方式获得.对于出现差异大的指标，可采用德尔菲法重新咨询并做相应调整，如表2所示.

表2 判断矩阵标度及含义

由所建立的指标权重判断表，可以构造一级指标，二级指标，三级指标权重判断矩阵，如表3～表8所示.

表3 一级指标A-U判断矩阵

表4 二级指标U1-X判断矩阵

表5 二级指标U2-X判断矩阵

表6 二级指标U3-X判断矩阵

表7 二级指标U4-X判断矩阵

表8 三级指标U-X判断矩阵

2.2 层次分析法计算指标权重

层次分析法是将定性分析和定量分析有机结合起来的分析决策方法，已经被广泛应用于决策、预测、评价等方面.这里在推算一、二级指标权重时采用层次分析法.具体步骤如下：

首先，用方根法计算出某层次因素相对于上一层次中某一因素的相对重要性，计算判断矩阵每一行元素的乘积：

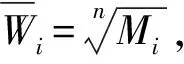
则W=(w1,w,…,wn)T即为所求权重向量.计算判断矩阵的最大特征根为

其中，(BW)i表示BW的第i个元素.

然后进行一致性检验，一致性指标和随机一致性比率分别为

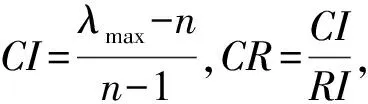
其中，RI为平均随机一致性指标，如表9所示.当CR<0.10时，通过一致性检验即确定权重向量为W=(w1,w2,…,wn)T.

表9 随机一致性指标RI的数值表

对于A-U判断矩阵，经计算得最大特征根λmax=4.14，权重向量ξ=(0.151 7，0.198 9，0.408 6，0.240 9)，一致性指标CI=0.02，随机一致性比率CR=0.019，通过一致性检验.

按上述办法，计算确定各二级指标相对于一级指标的最大特征值和权重向量为

由上可知，均通过一致性检验.在对高校创新创业教育评价时，对上述各层指标对权重进行合成运算，最终得到14个指标对目标层的合成权重为

W=(0.033 4, 0.094 2, 0.015 6, 0.008 4,0.129 1, 0.055 5, 0.014 3, 0.072 8, 0.307 1, 0.028 8,0.010 2, 0.020 5, 0.140 3, 0.069 9)T.

2.3 熵值法计算权重指标

熵是系统状态不确定性的度量，应用熵可以度量评价指标体系中指标数据所蕴含的信息量，并依次确定各指标的权重.应用熵值法计算权重的步骤如下：

计算第i项指标下，第j个评价对象标值xij的比重pij，

再计算第j项指标的熵值ej：

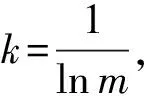
计算第j项指标的差异系数gj=1-ej,j=1,2,…,n, 确定指标权重：

则V=(v1,v,…,vn)T即为所求权重向量.按照上述步骤，计算确定三级指标判断矩阵X的权重向量，其中,m=4,n=14.每个评价标值比重为

计算各项指标的熵值：

[e1,e2,…,e14]T=[0.896 2，0.774 4，0.678 4，0.603 8，0.774 4，0.896 2，0.678 4，0.603 8，0.896 2，0.678 4，0.678 4，0.896 2，0.774 4，0.896 2]T.

计算各项指标的差异系数：

[g1,g2,…,g14]T=[0.103 8, 0.225 6, 0.321 6, 0.396 2, 0.225 6, 0.103 8, 0.321 6, 0.396 2, 0.103 8, 0.321 6, 0.321 6, 0.103 8, 0.225 6, 0.103 8]T.

最后确定指标权重向量为

V=[0.031 7, 0.068 9, 0.098 2, 0.121 0, 0.068 9, 0.031 7, 0.098 2, 0.121 0, 0.031 7, 0.098 2, 0.098 2, 0.031 7, 0.068 9, 0.031 7]T.

2.4 组合赋权法计算权重指标

层次分析法考虑了专家的知识和经验，虽然指标权重的排序往往具有较高的合理性, 但可能会形成主观偏差.熵值法充分挖掘了原始数据本身蕴涵的信息，通过决策矩阵客观计算权重，但无法反映专家的知识和经验.为了均衡主观与客观的优势与缺陷，将层次分析法的经验优势和熵值法的客观质量优势相结合是一种有效的赋权方法，而且该方法在不同领域都得到了很好的应用[6-8].组合赋权有多种计算方式，这里采用文献[7]中的方法，即根据拉格朗日乘数法求解相对信息熵最小化问题得到的最优组合赋权权重为

将2.2节采用层次分析法和2.3节采用熵值法计算的权重按照上述公式合成最终得到:

ω=[ω1,ω2,…,ω14]T=[0.040 4，0.099 9，0.048 6，0.039 6，0.117 0，0.052 0，0.066 0，0.076 4，

0.122 4，0.086 5，0.039 3，0.031 6，0.122 0，0.058 4]T.

3 结果分析

从2.4节组合赋权法获得的权重向量看到，按照CIPP评价原则构建的创新创业评价体系，准则层中各指标权重从大到小依次为创新创业过程、创新创业成果、创新创业投入和创新创业背景.其中，创新创业过程在创新教育指标体系中所占比例为0.285 3，在很大程度上直接影响高校创新创业教育的质量和发展水平.创新创业课程为学生提供了相对全面和系统的理论知识，而通过创客空间、孵化基地、校企合作企业等实践平台实施创新创业实践活动.只有这样，才能提升学校创新创业教育成果及实效.

创新创业教育成果在创新创业教育指标体系中所占比例为0.250 9，排在第二位.作为高校创新创业教育活动成效的体现，创新创业教育成果如学生创业率、创业立项数目、科研项目、专利授权项目等，综合反映了高校创业活动的水平和层次.

创新创业投入在创新创业教育指标体系中所占比例为0.235，排在第三位.创新创业投入是高校开展创新创业教育所需的资源投入及运行效率，更是高校创新创业教育质量的保障.

创新创业背景在创新创业教育指标体系中所占的比例为0.228 5，虽然这个比例相对较小，但在推进高校创新创业教育发展过程中，高校开展创业教育的内外部环境对创新创业成果的取得也起着非常重要的作用.

在方案层中，所在城市创新创业活跃度起关键作用，因此要加强城市创新创业理念和环境氛围；创新创业投入评价要素中，创新创业人力投入有重要地位，因此要加强创新创业的师资建设和投入；创新创业过程评价要素中，理论教学所占比重较大，所以要提升学校创新创业理论课程教学质量；创新创业成果评价要素中，创业率和就业率具有重要地位.