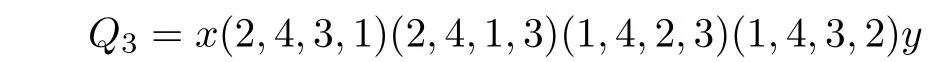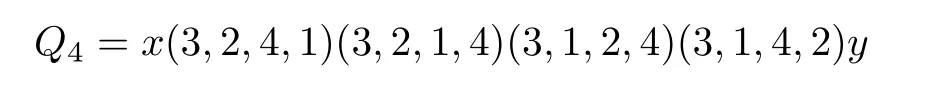由单圈图生成的凯莱图的广义3 连通度
王燕娜 周波
(1. 广东交通职业技术学院基础教学部,广州,510650;2. 华南师范大学数学科学学院,广州,510631)
1 Introduction
As usual,we denote byV(G)andE(G)the vertex set and edge set of a graphG. For a connected graphGand an integerkwith 2≤k ≤|V(G)|,the generalizedkconnectivity of a graphGis defined as[2,3,8]
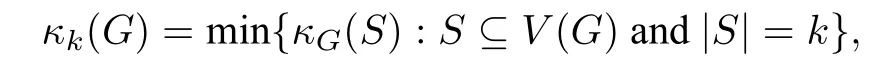
whereκG(S)is the maximum numberℓof edge disjoint treesT1,··· ,TℓinGsuch thatV(Ti)∩V(Tj)=Sfor every pair of distinct integersi,jwith 1≤i,j ≤ℓ. In the following,we call suchℓtrees asℓinternally disjoint trees connectingSinG.
Ifk=2,thenκk(G)is the smallest value of the maximum number of pairwise vertex disjoint paths between any vertex pair ofG,which is the ordinary(vertex)connectivity ofG[1]. Ifk=|V(G)|,thenκk(G)is the maximum number of pairwise edge disjoint trees ofG[9,10]. The generalizedkconnectivity may be used to measure the reliability and security of a network in whichknodes are users and other nodes are switchers.
LetXbe a group with identitye, and lete/∈S ⊆X, whereSis closed under inversion. The Cayley graph Cay(X,S) is a graph with vertexXsuch thatgandhforg,h ∈Xare adjacent if and only ifh=gsfor somes ∈S. We say Cay(X,S) is a Cayley graph onXgenerated byS. Denote Sym(n)the group of all permutations on[n] ={1,··· ,n}. By(p1,··· ,pn),we denote the permutationσsuch thatσ(i) =pifori ∈[n], and by [i,j] with 1≤i which swaps the objects at positionsiandj. LetTbe a set of transpositions from[n]. The(transposition)graph ofT, denoted byG(T), is the graph with vertex set [n] such that, fori,j ∈[n], verticesiandjare adjacent if and only if [i,j]∈T.It is known that the Cayley graph Cay(Sym(n),T) is connected if and only ifG(T) is connected. IfG(T) is the star, then Cay(Sym(n),T) is called a star graph, denoted bySn. IfG(T) is the path, then Cay(Sym(n),T)is called a bubble sort graph,denoted byBn. IfG(T)~=Cn(thenvertex cycle),then Cay(Sym(n),T)is called a modified bubble sort graph,denoted byMBn. IfG(T)is a general tree,then we denote by Tnthe graph Cay(Sym(n),T). IfG(T)is a general unicyclic graph,then we denote by Unthe graph Cay(Sym(n),T). In this case,we also say that Unis generated byG(T). The generalized 3 connectivities of various Cayley graphs,for example,the star graph,the bubble sort graph,the modified bubble sort graph and even Tnfor any general treeG(T)have been determined,see,e.g.,[7,6,11,12],to mention just a few. In this article, we show that the generalized 3 connectivity of Unfor any general unicyclic graphG(T)isn −1 forn ≥3. We use the techniques developed in the above papers,especially in[6]. Forv ∈V(G), denote byNG(v) the set of neighbors ofvinG, and letδG(v) =|NG(v)| andNG[v]=NG(v)∪{v}. For a subsetS ⊆V(G),denote byG[S]the subgraph ofGinduced byS. Forx,y ∈V(G),a path fromxtoyinGis called an(x,y) path. Forx ∈V(G)andY ⊂V(G),an(x,Y) path is an(x,y) path inGfor somey ∈Y,and any other vertex of the path(if exists any)are not in{x}∪Y. Lemma 2.1([1]) LetGbe akconnected graph, and letx ∈V(G) andY ⊆V(G){x}with|Y|≥k. Then there arekinternally vertex disjoint(x,Y) paths whose terminal vertices are distinct inY. Lemma 2.2([4])LetGbe a connected graph with minimum degreeδ. Thenκk(G)≤δfor 3≤k ≤|V(G)|. Furthermore,if there exist two adjacent vertices of degreeδinG,thenκk(G)≤δ −1. Lemma 2.3([4])LetGbe a connected graph withnvertices. Ifκ(G) = 4k+r, wherekandrare two integers withk ≥0 andr ∈{0,1,2,3},thenκ3(G)≥3k+. Moreover,the lower bound is sharp. Lemma 2.4([7]) Forn ≥3,κ(Tn)=n −1. Lemma 2.5([6]) Forn ≥3,κ(MBn)=nandκ3(MBn)=n −1. Suppose thatn ≥3. Recall that Un= Cay(Sym(n),T) whenG(T) is unicyclic. Obviously, Unis ann! vertex regular graph of degreen. Suppose thatG(T) ≇Cn. ThenG(T)has a leaf(a vertex of degree one),and we assume thatnis a leaf ofG(T)withn −1 being its unique neighbor. Fori ∈[n],let Symi(n)denote the set of all permutations of[n]{i}. Let Similarly, ifG(T) is a tree, then we assume thatnis a leaf ofG(T) withn −1 being its unique neighbor,andV(Tn)can also be partitioned intoV1,··· ,Vnand~= Tn−1,where= Tn[Vi]fori ∈[n]. IfQ=v1···vris apathinagraphG, thenQ−denotes thepathvr···v1. Foredge disjoint treesT1,···,Ts,if thegraph with vertexsetV(Ti)andedgesetE(Ti)isatree,thenwe denote this tree byT1+···+Ts. Lemma 2.6LetGbe a graph obtained from two vertex disjointkconnected graphsG1andG2by addingtedges betweenG1andG2such that any two edges are not adjacent. Ift ≥k ≥1,thenκ(G)≥k. ProofLetv1andv2be any two vertices ofG. It suffices to show that there arekinternally vertex disjoint paths betweenv1andv2. Ifv1,v2∈V(G1) orv1,v2∈V(G2), this is obvious asGiiskconnected fori=1,2. Assume thatv1∈V(G1)andv2∈V(G2). Denote thetedges betweenG1andG2byxiyifori=1,··· ,t. Note thatt ≥k. LetS={x1,··· ,xk}andS∗={y1,··· ,yk}. Obviously,|S|=|S∗|=k. AsG1iskconnected,we have by Lemma 2.1 that ifv1̸∈S,there arekinternally vertex disjoint(v1,S) pathsL1,··· ,Lksuch thatxi ∈Lifori= 1,··· ,k. Ifv1∈S,sayv1=x1,then there exists a(v1,S) path of length zero. So, there arekinternally vertex disjoint (v1,S) pathsL1,··· ,Lksuch thatxi ∈Lifori= 1,··· ,k. Similarly, there arekinternally vertex disjoint (v2,S∗) pathsQ1,··· ,Qksuch thatyi ∈Qifori=1,··· ,k. Now we can obtainkinternally vertex disjoint(v1,v2) paths:Li+xiyi+fori=1,··· ,k. Remark 2.1Suppose that{i,j} ⊂[n]withn ≥3. Note that Tn[Vi ∪Vj]may be obtained fromandby adding (n −2)! edges betweenand, in which any two edges are not adjacent. By Lemma 2.4,κ() =κ() =κ(Tn−1) =n −2. As (n −2)!≥n −2, we haveκ(Tn[Vi ∪Vj])≥n −2 by Lemma 2.6. On the other hand,the minimum degree of Tn[Vi ∪Vj]isn −2,soκ(Tn[Vi ∪Vj])≤n −2. Thus,κ(Tn[Vi ∪Vj])=n −2,see[7]. We need some lemmas that are used in the proof. Lemma 3.1κ(U4)=4. ProofIf U4~=MB4,then by Lemma 2.5,we haveκ(U4) = 4. Suppose that U4≇MB4. As the minimum degree of U4is 4,κ(U4)≤4. In the following,we show thatκ(U4)≥4. Letxandybe any two vertices of U4. It suffices to show that there are 4 internally vertex disjoint paths betweenxandy. Case 1xandylie in the same main part of U4. Assume thatx,yare in. Note that~=MB3. By Lemma 2.5,κ(MB3) = 3. Thus there are 3 internally vertex disjoint (x,y) paths, sayL1,L2,L3, in. As U4[V(U4)V1] is connected, there is an(x′,y′) pathQin U4[V(U4)V1]. It thus follows thatL1,L2,L3,xx′+Q+y′yare 4 internally vertex disjoint(x,y) paths. Case 2xandylie in different main parts of U4. Assume thatxlies inandylies in U23. Case 2.1x′∈V2andy′∈V1. Note thatx= (3,4,2,1)or(4,3,2,1), andy= (3,4,1,2)or(4,3,1,2). Suppose without loss of generality thatx=(3,4,2,1). Ify=(3,4,1,2),thenQ1=xy,Q2=x(4,3,2,1)(4,3,1,2)y, and are 4 internally vertex disjoint(x,y) paths. Ify=(4,3,1,2),thenQ1=xx′y,Q2=xy′y, and are 4 internally vertex disjoint(x,y) paths. Case 2.2x′∈V2andy′/∈V1,orx′/∈V2andy′∈V1. Assume thatx′∈V2andy′/∈V1. Assume thaty′∈V3. Thenx= (3,4,2,1)or(4,3,2,1), andy= (1,4,3,2)or(4,1,3,2). Suppose without loss of generality thatx= (3,4,2,1). Ify= (1,4,3,2),then are 4 internally vertex disjoint(x,y) paths. Ify=(4,1,3,2),then are 4 internally vertex disjoint(x,y) paths. Case 2.3x′,y′∈V3orx′,y′∈V4. Assume thatx′,y′∈V3. Thenx= (2,4,3,1) or (4,2,3,1), andy= (1,4,3,2) or (4,1,3,2).Suppose without loss of generality thatx=(2,4,3,1). Ify=(1,4,3,2),then are 4 internally vertex disjoint(x,y) paths. Ify=(4,1,3,2),then are 4 internally vertex disjoint(x,y) paths. Case 2.4x′∈V3andy′∈V4,orx′∈V4andy′∈V3. Assume thatx′∈V3andy′∈V4. Thenx= (2,4,3,1) or (4,2,3,1), andy= (1,3,4,2) or(3,1,4,2). Suppose without loss of generality thatx=(2,4,3,1). Ify=(1,3,4,2),then are 4 internally vertex disjoint(x,y) paths. Ify=(3,1,4,2),then are 4 internally vertex disjoint(x,y) paths. Thus there are 4 internally vertex disjoint paths betweenxandyin all cases. The result follows. Lemma 3.2Forn ≥3,κ(Un)=n. ProofBy Lemma 2.5,it is true forn=3. Suppose thatn ≥4. We prove the result by induction onn. By Lemma 3.1,it is true forn=4. Suppose thatn ≥5 and it is true for Un−1. If Un~=MBn, then by Lemma 2.5, we haveκ(Un) =n. Suppose that Un≇MBn. As Unisnregular, we haveκ(Un)≤n. So it suffices to show thatκ(Un)≥n, or equivalently, for any two verticesxandyof Un,there areninternally vertex disjoint paths betweenxandy. Case 1xandylie in the same main part of Un. Assume thatx,ylie in. Note that~= Un−1. By the induction hypothesis,κ() =n−1,so there aren−1 internally vertex disjoint(x,y) paths in,sayL1,··· ,Ln−1. As Un[V(Un)V1] is connected, there is an (x′,y′) pathQin Un[V(Un)V1]. It thus follows thatL1,··· ,Ln−1andxx′+Q+y′yareninternally vertex disjoint(x,y) paths in Un. Case 2xandylie in different main parts of Un. Assume thatxlies inandylies in. Note that(n −2)!≥n −1 forn ≥5. Case 2.1x′/∈V2andy′/∈V1. We may choosen −1 vertices,sayz1,··· ,zn−1,ofV1such that∈V2fori=1,··· ,n −1. LetS={z1,··· ,zn−1}andS∗={,··· ,}. Clearly,|S|=|S∗|=n−1. By the induction hypothesis,κ()=n −1,so by Lemma 2.1,there aren −1 internally vertex disjoint(x,S) pathsL1,··· ,Ln−1insuch thatzi ∈Lifori= 1,··· ,n −1. Similarly, there aren −1 internally vertex disjoint(y,S∗) pathsQ1,··· ,Qn−1in,such that∈Qifori=1,··· ,n −1. As Un[V(Un)(V1∪V2)]is connected,there is an(x′,y′) pathQin Un[V(Un)(V1∪V2)]. ThenLi+zi+fori=1,··· ,n−1,andxx′+Q+y′yareninternally vertex disjoint(x,y) paths in Un. Case 2.2x′∈V2andy′∈V1. We may choosen −2 vertices different fromy′, sayz1,··· ,zn−2, ofV1such that∈V2fori=1,··· ,n−2. LetS={z1,··· ,zn−2,y′}andS∗={,··· ,,x′}. Clearly,|S|=|S∗|=n−1.By the induction hypothesis,κ()=n−1,so by Lemma 2.1,there aren−1 internally vertex disjoint(x,S) pathsL1,··· ,Ln−1insuch thatzi ∈Lifori= 1,··· ,n −2,andy′∈Ln−1. Similarly,there aren −1 internally vertex disjoint (y,S∗) pathsQ1,··· ,Qn−1in, such that∈Qifori=1,··· ,n−2,andx′∈Qn−1. ThenLi+zi+fori=1,··· ,n−2,xx′+andLn−1+y′yformninternally vertex disjoint(x,y) paths in Un. Case 2.3x′∈V2andy′∈/V1,orx′∈/V2andy′∈V1. Assume thatx′∈/V2andy′∈V1. We may choosen −2 vertices,sayz1,··· ,zn−2,ofV1different fromy′such that∈V2fori=1,··· ,n −2,and choose a vertex,sayw,ofV2such thatw′∈/V1. LetS={z1,···,zn−2,y′}andS∗={··· ,,w}.Clearly,|S| =|S∗|=n−1. By the induction hypothesis,κ()=n−1,sobyLemma2.1,therearen −1internallyvertex disjoint(x,S) pathsL1,··· ,Ln−1insuch thatzi ∈Lifori=1,··· ,n −2,andy′∈Ln−1. Similarly,there aren −1 internally vertex disjoint(y,S∗) pathsQ1,··· ,Qn−1insuch that∈Qifori=1,··· ,n−2,andw ∈Qn−1. As Un[V(Un)(V1∪V2)]is connected,there is an(x′,w′) pathQin Un[V(Un)(V1∪V2)].ThenLi++fori= 1,··· ,n −2,Ln−1+y′yandxx′+Q+w′w+areninternally vertex disjoint(x,y) paths in Un. The result follows by combining the above cases. Now,we are ready to prove the main result. Theorem 3.1Forn ≥3,κ3(Un)=n −1. ProofIt is true forn=3 by Lemma 2.5. Suppose thatn ≥4. We prove this statement by induction onn. By Lemma 3.1,κ(U4) = 4. So, by Lemma 2.3,κ3(U4)≥3. Asκ(U4) is 4 regular, we haveκ3(U4)≤3 by Lemma 2.2. Thusκ3(U4)=3. That is,the statement is true ifn=4. Suppose thatn ≥5 and the statement is true for Un−1. If Un~=MBn,then by Lemma 2.5,we haveκ3(Un)=n−1. Suppose that Un≇MBn. As Unisnregular,we haveκ3(Un)≤n−1 by Lemma 2.2.So it suffices to show thatκ3(Un)≥n −1. LetSbe an arbitrary vertex subset of Unwith|S| = 3,sayS={x,y,z}. Then it suffices to show that there aren −1 internally disjoint trees connectingSin Un. Case 1x,yandzlie in some common main part of Un. Assume thatx,y,zlie in. By the induction hypothesis,κ3()=n −2,so there aren −2 internally disjoint trees connectingS,sayT1,··· ,Tn−2,in. As Un[V(Un)V1]is connected,there is a spanning treeTin Un[V(Un)V1]. ThusT1,··· ,Tn−2andT+x′x+y′y+z′zaren −1 internally disjoint trees connectingSin Un. Case 2x,yandzlie in two different main parts of Un. Assume thatx,ylie in U1n−1andzlies in U2n−1. Recall thatκ() =n −1. So there aren −1 internally vertex disjoint(x,y) paths,sayL1,··· ,Ln−1,in. Choosen −1 distinct verticesx1,··· ,xn−1fromL1,··· ,Ln−1such thatxi ∈V(Li)fori= 1,··· ,n −1. Note that at most one of these paths has length one. If there is indeed such a path of length one,sayL1,then in this case,we choosex1=x. LetZ={,··· ,}. Obviously,|Z|=n −1. Asκ(Un[V(Un)V1])≥n −1,we have by Lemma 2.1 that there aren −1 internally vertex disjoint(z,Z) pathsQ1,··· ,Qn−1in Un[V(Un)V1]such that∈Qifori= 1,··· ,n −1. NowTi=Li++Q− ifori= 1,··· ,n −1 aren −1 internally disjoint trees connectingSin Un. Case 3x,yandzlie in three different main parts of Un. Assume thatxlies in,ylies inandzlies in. Evidently,we have eitherx′/∈V2orx′/∈V3. Assume thatx′/∈V2. Recall thatκ(Un[V1∪V2])≥n −1. So there aren −1 internally vertex disjoint (x,y) paths, sayL1,··· ,Ln−1, in Un[V1∪V2]. Asx′/∈ V2, all neighbors ofxinL1,··· ,Ln−1are in neighbors,which are denoted byx1,··· ,xn−1. LetZ1={,··· ,}. Assume that 2 appears in thejth position ofx. Clearly,j ̸=n −1. Ifx[j,n −1] is a neighbor ofx, then(x[j,n −1])′∈V2, and thus|Z1∩V2| = 1. Ifx[j,n −1] is not a neighbor ofx, then/∈V2fori=1,··· ,n −1,and thus|Z1∩V2|=0. It thus follows that|Z1∩V2|≤1. Assume that{··· ,}/∈V2. LetZ2={x′,,··· ,}. Clearly,|Z2| =n −1. Asκ(Un[V(Un)(V1∪V2)])≥n −1,by Lemma 2.1,there aren −1 internally vertex disjoint(z,Z) pathsQ1,··· ,Qn−1in Un[V(Un)(V1∪V2)]such that∈Qifori=1,··· ,n −2,andx′∈Qn−1. NowTi=Li++fori=1,··· ,n −2,andQn−1+x′x+Ln−1formn −1 internally disjoint trees connectingSin Un. The result follows by combining the above cases. Remark 3.1This note shows that the generalized 3 connectivity of the Cayley graph Unon symmetric group of ordern ≥3 isn −1 if the transposition graph is any unicyclic graph,that is,there aren −1 internally disjoint trees connecting any three vertices in Un. So the upper bound forκ3(G)in Lemma 2.2 when there exist two adjacent vertices of minimum degree inGis attained.
2 Preliminaries
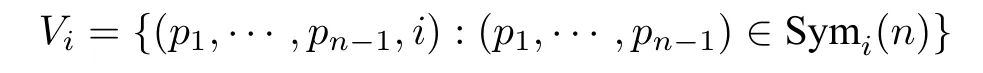
3 Main result