多尺度随机系统的渐近行为

李楠楠 解龙杰

(江苏师范大学,数学与统计学院,徐州,221000)

1 引言

自然界中的许多现象都具有多尺度特征或多尺度效应,并且,人们对这些现象的观察及测量也常在不同尺度（分辨率）下进行(参见[3,13,16,21,24,26,30]).数学上,多尺度系统能够很好地将这些现象的本质特征反映出来.近年来,多尺度问题及相关理论被广泛应用于海洋大气、复合材料、生命科学和金融等领域,其研究热度不断上升.

多尺度系统往往比较复杂,处理起来也相对困难.平均化方法是处理多尺度问题的一个强有力的工具,它通过构造一个“平均化方程”来简化原系统,使化简后的方程不再涉及尺度的分离.本文首先介绍快慢随机系统的平均化原理的强、弱收敛,特别侧重于噪音所带来的正则化作用.然后,介绍原系统与其平均化方程的波动估计.这两个方面分别对应于或类似于概率论中的大数定律与中心极限定理.而对于更一般的多尺度随机系统,我们将介绍其扩散逼近,这一问题与偏微分方程中的同质化有紧密联系.最后,我们考虑一类特殊的系统: 随机Langevin 方程,分别给出由布朗噪音驱动和Lévy 噪音驱动的随机Langevin 方程的Smoluchowski Kramers 逼近.

2 平均化原理

考虑如下的随机微分方程:

其中,d≥1 为空间维数,F:Rd×Rd →Rd为可测函数（称为漂移系数）,Wt为定义在某概率空间(Ω,F,P)上的d维标准布朗运动,X=(Xt)t≥0为一个给定的遍历马氏过程,参数0<ε ≪1 代表了时间尺度的分离:以正常的时间尺度t变化,而X以时间尺度t/ε变化.因此,在方程(2.1)中,通常称为慢变量,用来代表实际中可以观测到的量,也是人们更关心的量;而X称为快变量,通常用来描述系统所处的快速变化的外界环境或者其他相关的影响因素.

因为方程(2.1)中涉及到两个时间尺度,所以直接研究(2.1)比较复杂.我们希望寻找一个简单的方程来近似地代替该方程. 由于在大多实际问题中,ε>0 非常小,因此问题即转化为研究该系统当ε →0 时的渐近行为.对于方程(2.1),可以比较直观地推测出其ε →0 时的极限: 假设X的唯一不变测度为µ(dx),则形式上,当ε →0 时,Xt/ε将收敛到其不变测度µ(dx),代入到方程(2.1)中,即可得将收敛于,其中满足

这里新的漂移系数为

这一结果称为平均化原理,方程(2.2)称为(2.1)的平均化方程, ¯F称为平均化系数.

一般地, 平均化原理的证明需要假设原方程的系数满足一定的正则性条件. 经典的平均化原理由前苏联数学家Bogoliubov (参见[6]) 对确定性的常微分方程首先建立. 这一理论后来被Khasminskii[17]推广到随机微分方程.在随机的情形,从概率的角度来说,可以按照多种方式收敛到. 这里我们主要介绍两种:

(i)强收敛(p阶矩收敛):对任意的p≥1,

(ii)弱收敛(依分布收敛):对任意的φ ∈Cb(Rd),

从结果上看,强收敛可以直接推出弱收敛.但强收敛往往需要更强的假设条件,并且强收敛的收敛速度也慢于弱收敛.在下面的定理中我们会具体介绍.

方程(2.1)相对来说仍然比较简单: 其快变量X不依赖于慢变量Y.然而,在描述一个复杂系统时,快、慢变量会完全偶合在一起.因此,我们需要考虑如下更一般的随机微分方程:

相比于(2.1),方程(2.4)由可乘噪音驱动,并且其快变量X会依赖于慢变量Y. 此时,仍然像之前那样直接推测其平均化方程不再可行.直观上,推导方程(2.4)的平均化方程可分为两步:

(1)当观察快变量时,慢变量几乎保持不动;

(2)当观察慢变量时,快变量几乎已经达到其平稳状态.

具体地,我们先来看快变量. 观察快变量合适的方式是对其做时间变换.令:=(以时间尺度tε来观察快变量),则可以验证满足如下方程:

这里,平均化漂移系数为

平均化的扩散系数为

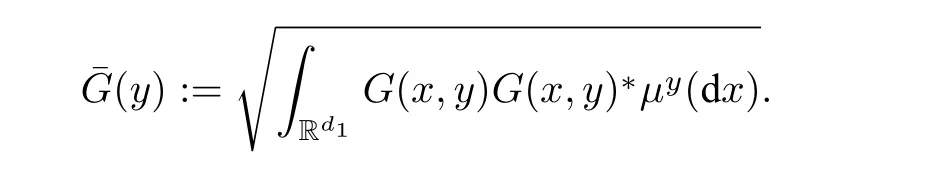
注1 需要指出的是,尽管平均化方程(2.2)和(2.6)中平均化系数的形式类似,但方程(2.4)的研究远比(2.1)复杂.实际上,对于强收敛,通常需要证明平均化后的系数满足Lipschitz 条件以保证平均化方程的强适定性.对于(2.3),我们只需要假设原方程(2.1)中的漂移系数F(x,y)关于y变量满足Lipschitz 连续性的条件,则容易验证¯F也满足Lipschitz 条件.但(2.7)中¯F的Lipschitz 连续性的验证要困难的多: 其涉及到不变测度µy(dx)关于参数y的正则性的研究.

目前,随机系统的平均化原理已经得到非常深入地研究.关于由布朗运动驱动的随机微分方程的平均化原理,可参见[11,18,20,25,35];关于由Lévy 噪音驱动的随机微分方程的平均化原理,可参见[4,31,34];关于随机偏微分方程的情形,可参见[7,10]及其中的参考文献. 下面,我们分别介绍两个具体的平均化原理强、弱收敛的结果,并给出其与经典结果的比较.这里,我们主要关心不规则系数的情形,从而体现出噪音对系统的正则化作用.在此之前,我们做一些基本的假设:

(Hσ) 扩散系数a=σσ∗一致非退化,即存在常数λ>1,使得对任意的x ∈Rd1和y ∈Rd2,有

(HG) 扩散系数G=GG∗一致非退化,即存在常数λ>1,使得对任意的x ∈Rd1和y ∈Rd2,有

(Hb) 漂移系数b满足如下的Lyapunov 条件:

假设(Hσ)和(Hb)保证凝固方程(2.5)存在唯一的不变测度(参见[29,36]).同时,假设(HG)将保证我们可以在不规则系数的条件下研究方程(2.4)的平均化原理.

我们有如下结果,参见[33,Theorem 2.1].为简单起见,以下所有结果的叙述中我们都假设系数有界.

定理1(强收敛)假设(Hσ),(HG),(Hb)成立,并且

如果σ ∈,G ∈且b,F ∈,其中δ,α>0,则对任意的T>0,有

其中,CT>0 为不依赖于δ和ε的常数.

注2 (i)假设(2.8)是必要的,因为当慢方程中的扩散系数G依赖于x(快变量)时,强收敛不一定成立(参见[22]).

(ii)虽然我们只假设了方程(2.4)中的漂移系数为Hölder 连续的,但在(Hσ)和(HG)的条件下,方程(2.4)仍存在唯一的强解.同时,也可以证明,从而平均化方程(2.6)同样存在唯一的强解,这体现了噪音的正则化作用.关于不规则系数下随机微分方程强适定性的更多介绍,可参见[40,41].

(iii)经典的平均化原理的结果都需要假设系数满足Lipschitz 连续或者局部Lipschitz 连续的条件,并且,在系数足够正则的情况下,强收敛的最优收敛速度为而估计(2.9)表明,当方程中的系数关于y变量（慢变量）为αHölder 连续时,强收敛的收敛速度为εα/2. 特别地,其收敛速度不依赖于方程中系数关于快变量的正则性.这与直观吻合: 在取极限的过程中,快变量被完全平均化,其不再出现在极限方程中.

关于方程(2.4)平均化原理的弱收敛,我们有如下结果(参见[32,Theorem 2.3]).

定理2(弱收敛)假设(Hσ),(HG),(Hb)成立. 如果σ,b,F,G ∈,其中δ,α> 0,则对任意的T>0 及φ ∈(Rd2),有

其中,CT>0 为不依赖于δ的常数.

注3 (i)对于平均化原理的弱收敛,我们只需要保证方程的弱适定性.由于噪音的非退化性,在上述系数Hölder 连续的假设条件下,原方程(2.4)及平均化方程(2.1)存在唯一的弱解.

(ii)估计(2.10)表明,当原方程的系数关于慢变量为αHölder 连续时,弱收敛的速度为α/2.特别地,当α=2 时,得最优的弱收敛速度为1.与强收敛的情形类似,上述的弱收敛也不依赖于系统关于快变量的正则性.

3 正态偏差

随机系统的平均化原理可以理解成一种泛函大数定律.其意义在于,我们可以利用平均化方程(2.6)近似地代替原方程(2.4),而平均化方程不涉及多尺度变量,从而更加简单.但极限方程(2.6)只有在ε →0 时才成立.在实际应用中,虽然ε很小,但其永远大于0,从而,会与其平均有一定的偏差.要研究其波动情况,自然地需要研究中心极限定理,即考虑标准化的过程

当ε →0 时的渐近行为.

为了更清楚地了解问题的困难所在,我们先考虑(2.4)中G=I(单位矩阵)的情况.此时,

其中, ˜Wt为一新的标准布朗运动,而新的扩散系数为

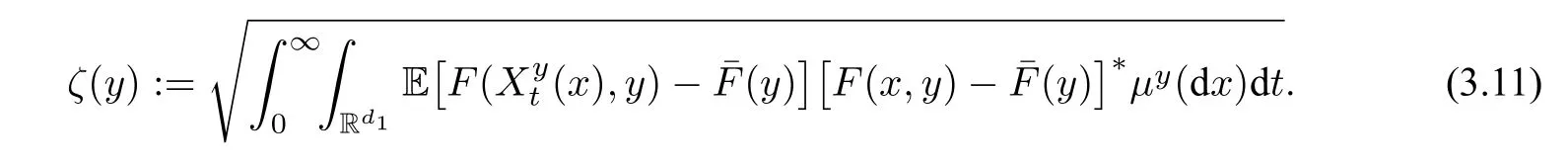
对于一般的随机系统,我们有如下结果(参见[33,Theorem 2.3]).关于多尺度随机偏微分方程正态偏差的研究,可参见[8,37].

定理3(正态偏差)假设(Hσ),(HG),(Hb)及(2.8)成立. 如果σ,b,F,G ∈,其中δ,ϑ>0,则对任意的T>0 及φ ∈(Rd2),有

CT>0 为不依赖于δ和ε的常数.

注4 特别地,估计(3.12)说明,当ϑ=1 时中心极限定理的最优收敛速度为

一个有趣的问题是: 能否找到一个分布不依赖于ε的过程,使得以ε阶强收敛到,即对任意的p≥1,存在常数Cp>0,使得

其中,扩散系数ζ由(3.11)定义. 但理论上一直没有能够给出证明.实际上,直到2004 年,Bakhtin和Kiffer[2]才证明了

其中,0<δ<(18+8d)−1.虽然得到了高于的收敛速度,但这个δ仍不是最优的.

4 扩散逼近

考虑如下多尺度随机微分方程:

其中,当ε →0 时,参数αε,βε,γε →0.特别地,当c=H ≡0,αε=时,方程(4.13)即为快慢方程(2.4). 相比于(2.4),方程(4.13)有如下两个主要特点:

(i)快方程中存在两个不同的时间尺度,分别由αε和βε刻画;

方程(4.13)的极限行为与偏微分方程中的同质化理论有密切联系(参见[14,19,23]).当αε=βε=γε=,且()的状态空间为紧集时,方程(4.13)首先由Papanicolaou,Stroock和Varadhan[27]进行了研究.而当c ≡0,αε=γε=的状态空间为全空间时,Pardoux 和Veretennikov 在一系列文章[28,29]中对(4.13)的极限进行了研究.需要指出的是,在全空间上(4.13)的研究要比紧集上困难的多,其关键在于求解全空间上带参数的Poisson 方程,并研究解的正则性.

对于方程(4.13),根据时间尺度收敛到0 的速度不同,其极限方程也不同. 具体需要分以下四种情况:当αε和收敛到0 的速度分别比γε和βεγε快时(情况1),方程(4.13)与方程(2.4)的平均化方程完全一致,也就是说,c和H变化的速度不够快,其作用并没有体现在极限方程中;当αε收敛到0 的速度比γε快而和βεγε同阶时(情况2),系数c的同质化作用将体现在极限方程中;当αε和γε同阶而αε收敛到0 的速度比βε快时(情况3),系数H的同质化作用将得以体现;最后,当所有的参数都同阶时(情况4),c和H的同质化作用将同时体现在极限方程中.

为了介绍(4.13)的极限方程,我们需要引入如下的Poisson 方程:

其中,y ∈Rd2为参数,

a(x,y) :=σσ∗(x,y).需要指出的是,虽然紧集上的Poisson 方程已经有了很深入的研究,但全空间上带参数的Poisson 方程(4.15)的研究却十分困难(见[32]).特别地,为了保证(4.15)解的存在唯一性,需要假设H满足如下条件:

在一定的正则性条件下,方程(4.15)存在唯一的解Φ(x,y). 对应于(4.14)中的情况1–4,我们分别定义平均化的漂移系数

以及平均化的扩散系数

我们有如下主要结果(参见[32,Theorem 2.3]).关于随机偏微分方程的扩散逼近,可参见[38].

定理4假设(Hσ),(Hb),(HG)及(4.16)成立,T>0 且δ ∈(0,1].

注5 上述结论中,对应于情况3 和4 的结论表明: 即使原系统中G ≡0(慢方程中没有噪音项),其极限方程中仍然会出现可乘的布朗噪音项.这主要是由慢方程中快速变化的H项的同质化导致的.

5 Smoluchowski Kramers 逼近

5.1 布朗噪音驱动

考虑一个质量为ε的小粒子在受外力、正比于速度的摩擦力及噪音作用下的运动.令表示t时刻粒子的位置,则根据牛顿第二定律,满足如下的随机Langevin 方程(参见[15]):

其中,F(x) : Rd →Rd表示外力项, ˙Wt为标准高斯白噪声,矩阵函数σ(x)代表噪声的强度,γ> 0为摩擦常数. 在一定的假设条件下,当ε收敛到0 时(即相比于惯性,摩擦力起主导作用),将L2(Ω)收敛到Xt,其中Xt满足

这一结果被称为Smoluchowski Kramers 逼近. 其意义在于: 对于小粒子, 我们可以用一阶方程(5.19)来近似代替二阶牛顿方程(5.18)来描述其运动.

然而,当摩擦常数依赖于物体的位置时,极限方程的形式将会不同.具体地,考虑如下随机系统:

其中,γ(x)为d×d矩阵值函数.此时,当ε →0 时将L2(Ω)收敛到Xt,其中Xt满足

这里的S(x):Rd →Rd被称为由噪音诱导的漂移系数,其第i个分量为

而M(x)满足Lyapunov 方程

特别地,如果γ(x)和Σ(x)可交换,即γ(x)Σ(x)=Σ(x)γ(x),则有M(x)=γ−1(x)Σ(x)/2.

关于Langevin 方程的Smoluchowski Kramers 逼近,目前已经有很多的研究结果,关于随机微分方程的情形可参见[5,12,15],而关于随机偏微分方程的情形可见[9]及其中的参考文献. 实际上,Smoluchowski Kramers 逼近的问题可以转化为扩散逼近问题.如果我们定义速度过程

则方程(5.21)可改写为:

注意到这只是方程(4.13)的一个特殊情况. 但区别在于,扩散逼近一般只能得到弱收敛(依分布收敛),而Smoluchowski Kramers 逼近的特殊之处在于,这里可以得到强收敛. 我们假设:

(A)矩阵γ(x)和σ(x)一致非退化,即存在常数λ>1,使得对任意的x ∈Rd,有

我们介绍如下结果(参见[39]).

定理5假设(A) 成立. 若γ ∈,F ∈且σ ∈, 其中0<δ,β≤1, 则对任意的T>0 及q≥1,有

其中,Xt为随机微分方程(5.21)的唯一强解,CT>0 为不依赖于ε和δ的常数.

5.2 Lévy 噪音驱动

下面,我们考虑由Lévy 噪音驱动的随机Langevin 方程的Smoluchowski Kramers 逼近.为简单起见,我们考虑一维空间的情形:

其中,Lt为旋转不变的α稳定过程,α ∈(1,2).与之前类似,我们引入速度过程

则方程(5.22)可改写为

有趣的是,与布朗噪音驱动的随机Langevin 方程不同,即使(5.22)中的摩擦常数依赖于物体的位置,其极限方程中仍不会出现新的由噪音诱导的漂移系数.

我们将证明如下结果.为了更清楚地介绍证明方法及关键技巧,我们假设系数充分光滑且有界.

定理6假设σ(x),γ(x)非退化.则对任意的T>0,有

其中,Xt满足如下随机微分方程:

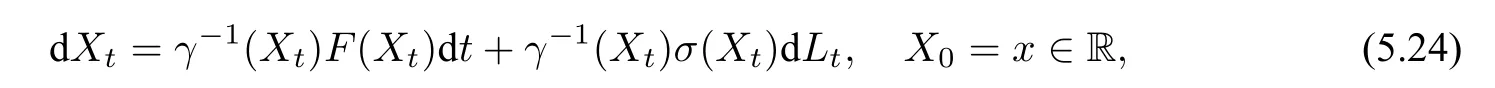
CT>0 为不依赖于ε的常数.

证明为简便起见,我们定义算子

及函数

可以验证

上式两边同时乘以ε1/α,并利用公式(5.25)可得

注意到,由Ψ(x,v)的定义我们有

且

从而,进一步有

此式与(5.24)相减并取期望,可得

其中, ˜Lt为一新的旋转不变的α稳定过程.由[40,Lemma 7.1],有

进一步有

从而可得

由Gronwall 不等式,即得(5.23).