基于非线性规划法沥青混合料配合比设计方法研究
李威
( 江苏高速公路工程养护有限公司,江苏 淮安 223001)
0 引言
国内常用的矿料级配设计理论有: 最大密度曲线理论,该理论下沥青混合料中粗颗粒少,细颗粒多,导致路面构造深度小,抗滑性差,沥青品质和含量变化对路面质量影响较大[1],基于此理论衍生的级配设计方法有:泰波改进的n 法、林绣贤的I 法等。 Weymouth 的粒子干涉理论是一种研究如何利用细颗粒填充粗颗粒之间间隙的理论, 如果粗细搭配比例不当, 则细颗粒材料将会影响粗颗粒材料之间的力的传递, 基于此理论衍生的级配设计方法有:CAVF 法[2-3]、贝雷法等。
文章将矿料组成设计进行数学模型转化,再用最小二乘法的思想数学模型进行化简, 转化为可以用非线性规划进行求解的形式, 其中结合CAVF 矿料组成设计方法,将CAVF 的结果转化为带有约束的非线性规划边界条件, 然后用非线性规划内部罚函数法将问题转化为可以进行迭代的形式,最后用最速下降法进行迭代运算。 根据计算结果来拌制沥青混合料性, 检验沥青混合料的性能,以检验方法的可行性。
1 矿料组成设计的计算方法推导
1.1 矿料组成设计的数学模型转化
矿料分档数量为n,各矿料的筛分结果以矩阵表示见式(1):

其中aij(i=1,2,…,m;j=1,2,…,n)是筛分结果中的第j 种矿料对应第i 种筛孔的质量通过百分率。
n 种矿料在沥青混合料中的质量比例组成系数,用列向量表示为:X=(x1x2… xn)T,其中Xj=(j=1,2,…,n),为第j 种矿料在混合料中所占的比例系数,满足如下条件,见式(2)~(5):
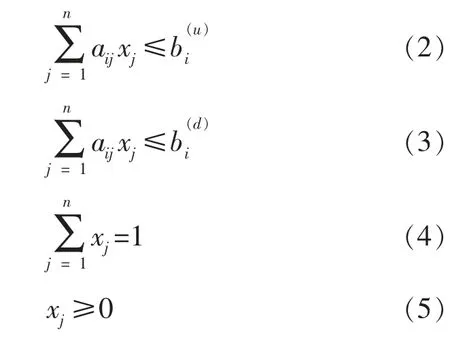
其中式(2)、(3)是沥青混合料级配上下边界,式(5)保证计算值为正,式(4)保证沥青混合料中的质量比例之和为1,当Xj=0 表示该种级料掺配比例为0,不参与混合料的组成设计。
1.2 最小二乘法和非线性规划应用
一般要求级配曲线尽量接近设计级配曲线中值,计算见式(6)。
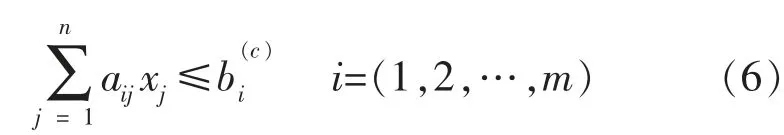
联立式(4)、(6)求解线性方程组。 筛孔孔径的个数一般大于矿料分档的个数,即m≥n,若R(A)≠R(B),其中R(A)是矩阵A 的秩,其中R(AB)是增广矩阵AB 的秩,则该方程组无解。 在这种无解的情况下,可以利用最小二乘法的思想,虽然不能完全满足条件,但可以使混合料各孔通过率与规范要求的级配曲线中值的平方和达到最小,结果见式(7)。

以式(2)、(3)、(4)、(5)为边界条件,以式(7)为目标,转化为带有约束非线性规划的问题。 带有约束非线性规划的问题可以用内部罚函数法,将通过增广目标函数而化成无约束极小化问题。
设有不等式约束问题
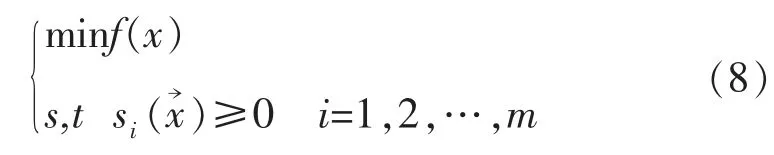
式中:si()为各类边界约束,为边界约束范围内的点;可将式(7)转化为无约束非线性规划,结果见式(9)。

1.3 最速下降法应用
式(9)的计算方法为迭代法中的最速下降法,其算法过程如下:①给定初始点X0,令K=0;②计算XK点的梯度,若梯度小于等于事先给定的非常小的正数ε 则终止, 否则, 下一步; ③令-Zk=-f′(xk), f′为一阶导数;④求使Zk=-f′(xk+λzk)最小的λ,记为λk,即最佳步长,令xk+1=xk+λkzk,转②。
1.4 CAVF 法转化为非线性规划的边界条件
CAVF 法计算公式如式(10)所示。
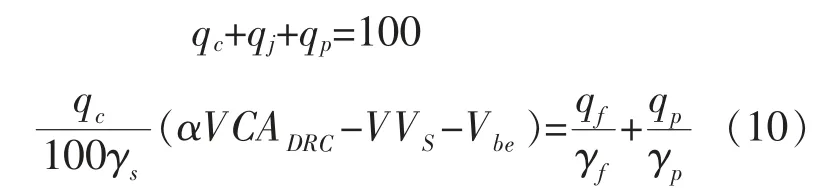
式中:qc、qf、qp、qd分别为粗集料重量%、 细集料重量%、矿粉重量%、沥青用量%;γs、γf、γp分别是粗集料毛体积密度、细集料表观密度、矿粉表观密度;VVs、VCADRC、α、Vbe分别是主骨架矿料空隙率、混合料设计空隙率、干涉系数和有效沥青体积,其中α 取0.9,Vbe取10 %。
因此只要按式(10)计算,就可以得出粗细集料的比例,并以此为边界条件,控制沥青混合料空隙率。
2 软件实例应用计算
手工迭代运算工作量大,运用软件可使混合料配合比设计事半功倍。 目前WPS 软件普及程度非常高,不仅可进行线性规划计算,还可进行表格绘图,实时将结果反映到图上,非常适合矿料组成设计。
矿料采用4 种不同的粒径, 经MPS 软件数据处理计算结果如图1 所示。
由图1 可知, 其合成级配曲线接近中值,但2.36 mm 和4.75 mm 的通过率在级配中值以下,其相关性能需进一步检测。
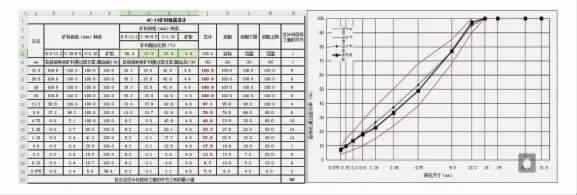
图1 矿料组成设计结果
3 路用性能分析
按图1 所示矿料组成比例拌制AC-13 沥青混合料,最佳油石比为4.9 %,并检测相关性能。
水稳定性计算结果见表1 和2。
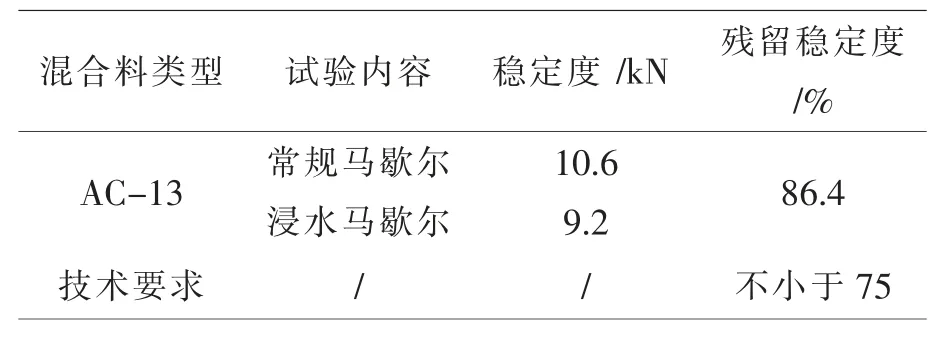
表1 沥青混合料浸水马歇尔试验结果

表2 沥青混合料冻融劈裂试验结果
低温弯曲试验结果如表3 所示。
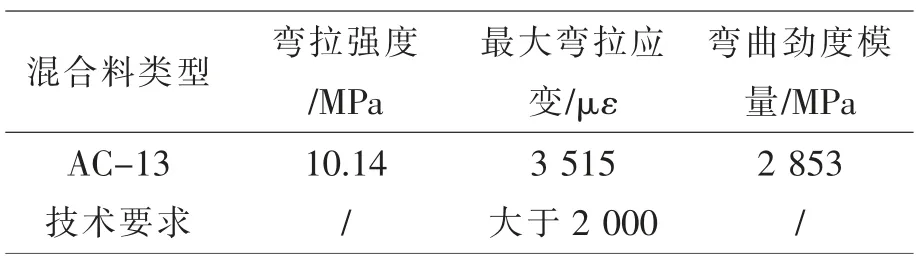
表3 沥青混合料弯曲试验结果
高温稳定性试验结果见表4 和5。

表4 沥青混合料马歇尔试验结果

表5 沥青混合料车辙试验结果
从表1~5 可以看出,沥青混合料高温性能、低温性能、水稳定性,均满足规范要求。
矿料主骨架间隙率VCADRC与混合料骨架间隙率VCAmix如表6 所示:

表6 VCADRC 与VCAmix 结果
由表6 可知,0.9 倍的VCADRC与VCAmix较为接近,但是干涉系数具体取值还需进一步研究。
4 结论
(1)通过将矿料组成设计问题用最小二乘的思想转化为非线性规划的问题,用迭代法中最速下降法来进行求解,从而找到一种快速设计矿料组成设计的计算方法, 并且与CFVA 法进行了结合,将CFVA法的计算结果转化为非线性规划的边界条件。
(2)对模拟计算出的矿料拌制混合料,检验其性能均符合规范要求,验证了WPS 矿料组成设计的可行性, 但对于其他矿料组成理论如何将其计算结果转化为非线性规划的边界条件需要进一步研究。

