多状态系统测试建模与测试点选取方法

王 鹏，于永利，李星新，刘晨光，孙也尊

(1.陆军工程大学(石家庄校区) 装备指挥与管理系，石家庄 050003;2.中国人民解放军32382部队，北京 100072;3.中国人民解放军32200部队，辽宁 锦州 121000)

测试性定义为产品能及时准确地确定其状态(可工作、不可工作或性能下降)，并隔离其内部故障的一种设计特性。需要指出的是，测试性不仅包括系统故障的测试，还包括正常和退化状态的测试。然而，对于系统可测试性的研究往往更多地关注于故障测试而在退化状态测试方面的研究较少。目前常见的测试性模型主要是在相关性模型基础上建立的，如逻辑模型、结构模型、信号流模型、多信号模型及混合诊断模型等[1]。这些测试性模型能够实现系统故障与测试相关关系的描述，但其测试分析过程均是在二态系统基础上进行的，忽略了系统的多状态特性，从而难以实现系统退化状态的测试性分析。

相较于二状态系统(只考虑正常和故障两种状态)，多状态系统(Multi-state system, MSS)考虑了系统及元件从正常到故障之间的一个或多个退化状态，能够通过定量的转移概率描述系统状态与元件状态、系统状态与系统故障之间的关系，多状态信息对揭示复杂系统潜在的失效机理和规律至关重要，有利于提高系统故障诊断与预测效率，降低诊断成本[2]。目前，在多状态系统模型的基础上，研究主要集中在多状态系统可靠性建模与分析[3-9]、可靠性优化设计[10-14]、维修管理策略[15-20]等方面，这些研究通过分析系统的状态转移关系，结合初始状态求得系统的状态分布，从而对系统的可靠性进行分析与优化设计、制定维修策略，而对多状态系统测试优化问题的研究相对较少。

针对二态系统的测试优化问题，国内、外学者进行了广泛研究并提出了许多优化方法，主要包括基于信息理论的排序方法[21-23]和基于组合优化的搜索算法[24-26]。前者主要利用信息熵来定义测试对于故障检测和故障隔离的有用程度，并以此作为测试的权重，优先选择权重高的测试，直到满足测试性指标要求为止；后者以测试代价最小为目标函数，以测试性指标要求为约束条件建立数学模型，然后采用智能优化算法求解。

由于考虑了介于正常和故障的中间状态，多状态系统测试不仅要考虑系统的故障诊断问题，还需考虑系统及元件中间状态的诊断问题。而多状态系统的测试优化问题就是通过分析系统测试与系统状态之间的关系，在满足测试性指标要求的情况下，综合权衡测试代价与系统状态信息获取问题。测试与系统状态的相关分析是进行系统测试优化的基础。因此，本文首先分析多状态系统特点，对多状态系统测试性进行建模；其次在所建模型基础上，分析了系统的状态-测试相关关系；最后提出了考虑故障检测率、故障隔离率与状态检测率的测试点选取方法。

1 状态测试相关建模

1.1 多状态系统描述

设一个多状态系统由n个元件组成，其中任意元件m具有hm+1个状态，则其状态空间按照由差到好的顺序依次排列描述为sm={0,1,…,hm} ，其中0状态为元件的故障状态，hm状态为元件的正常工作状态，其余状态介于故障与正常之间。与元件m的状态空间相对应的性能水平为gm={gm0,…,gmhm}，其中gmk为元件m处于状态k(k∈sm)时的性能水平。元件m处于不同状态下的概率可以表示为集合pm={pm0,…,pmhm} ，其中pmk为元件m处于状态k下的概率。系统的状态为S(t)={s1(t),s2(t),…,sn(t)}，其中si(t)∈si。设Ln={g10,…,g1h1}×…×{gn0,…,gnhn}为所有系统元件性能水平的组合空间；整个系统可能出现n个状态，系统处于状态i(i∈{1,…,n} )时的性能表示为vi，M={v1,…,vn}为系统性能水平空间，以Gi(t)表示t时刻元件i的性能水平，映射φ(G1(t),…,Gn(t)):Ln→M表示为元件性能水平空间与系统性能水平空间的转换关系，则系统性能水平函数描述为

V(t)=φ(G1(t),…,Gn(t))

(1)

也称为系统的结构函数，表示元件性能与系统性能之间的传递关系，它由系统的结构关系以及元件性能属性共同决定。

1.2 MSS测试建模

在二态系统的测试性建模方面，以信息流模型、多信号模型以及混合诊断模型为主的相关性模型得到了广泛应用[1]。多信号模型通过获取系统的故障-测试相关信息，以满足规定的故障检测率和故障隔离率为约束条件，进而搜寻代价最小的测试。对多状态系统测试而言，不仅需要测试能够发现并隔离系统故障，还需获取系统的状态信息。因此，在进行多状态系统测试性设计时，需要对多状态系统的状态传递过程进行分析，获得包括故障信息在内的系统状态-测试相关信息。由于多信号模型是对系统结构的建模，无法得到系统功能相关的状态信息，因此不适用于多状态系统的测试建模分析。本文提出一种基于结构和功能建模的多状态系统测试相关模型，该模型根据产品层次化结构和功能设计信息，以功能为底层建模对象，通过功能的性能指标判断各功能的状态，并以性能状态作为各单元功能相关的输入用以动态描述功能的作用关系，从而实现系统状态-测试相关关系的描述。由于认知和随机的不确定性的存在，建模过程中考虑了系统发生故障后的传播不确定性、测试的不确定性以及模型认知机理的不确定性。对于系统单元性能的故障判断问题，通过专家经验、历史数据、相似性判断3种经验知识对系统故障进行诊断。总体建模思路如图1所示。

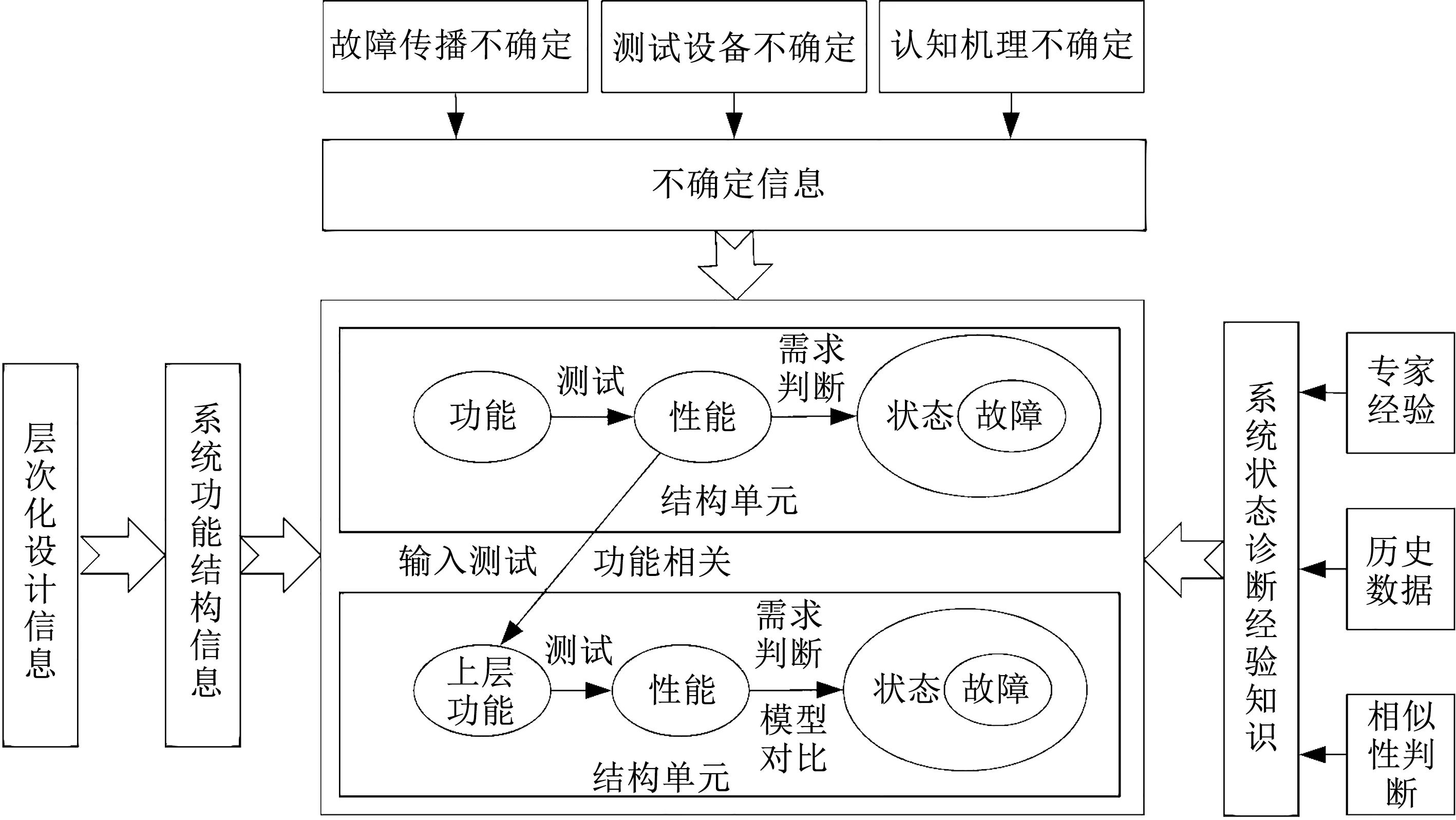
图1 建模总体思路Fig.1 General idea of modeling

系统测试模型可以描述为一个有向图G={C,CF,FM,E,T,D}，其中C={c1,…,cn}表示系统n个结构单元的有限集合；CF={cf1,…,cfr}是系统组成单元r个功能的有限集合，每个功能依赖于相应的系统组成单元；FM={fm1,…,fml}是系统l个故障模式的有限集合，每个故障模式依赖于相应组成单元的功能；E={eij}表示由功能i指向功能j的有向边的集合，描述系统功能的流向关系；T={t1,…,tk}表示系统中k个可用测试点的有限集合，测试点用于测试某个功能的输出信号；D=[dij]是单元功能-测试依赖关系矩阵，以功能为行，测试为列，若从功能i的输出信号能够经过有向边到达测试j，则dij=1，否则dij=0，在考虑到故障传播的不确定性和测试的不确定性情况下，若功能i的输出信号能够经过有向边到达测试j的概率为pij，测试tj的可靠性为σtj，则dij=pijσtj。

2 多状态系统测试选择方法

2.1 状态与测试问题考虑

系统功能的输出信号是否符合规定的性能值是判断系统是否故障的依据。因此，通过在功能输出位置加入测试点进行测试，根据得到的结果是否符合规定的性能指标即可判断系统是否存在故障。然而，虽然测试结果能够判断系统是否存在故障，却无法定位故障源。要判断单元的功能状态，不仅需要获得该功能的输出信号，还应获取相应的输入信号。要获取系统所有单元功能的输入输出，所需测试代价高昂，此外在很多情况下(限于测试所占有的空间，质量或者技术条件)，单元的功能输出信号无法获取。因此，多状态系统的测试需要考虑两方面问题：1)如何建立系统测试与单元功能状态之间的关系。2)如何选择能够满足系统要求的测试。

图2 多状态系统结构Fig.2 Multi-state system structures

通过上述分析可知，除同质系统外，仅凭系统输出测试无法确定系统的每个状态。为了确定系统状态，首先需要对系统各状态与测试的关系进行分析，其次考虑增加合理的测试，对多个测试结果进行综合分析判断系统状态。

2.2 状态-测试相关分析

为了建立测试与功能状态的关系，设系统中测试点ti相关的功能集合为RCFti={cfj|dji=1,cfj∈CF}。在这里定义系统测试点ti的测试取值空间为

H(ti)=φi(g1,…,gn)

(2)

式中φi(·)为测试结构函数，表示各单元功能的性能水平空间与测试取值空间的映射关系，与时间t无关，由各元件到测试点的结构关系及性能属性确定。若单元功能cfm处于状态smk时测试ti的取值与该功能不在状态smk时的取值空间无交集，则测试ti可以检测状态smk。则测试ti能够检测的状态集Hh(ti)满足：

(3)

式中H(ti|gmk)为功能cfm在状态smk下，测试ti的取值空间。

当测试ti=r∈H(ti)时，与其相应的功能状态组合空间为

(4)

若功能状态组合空间中的元素包含某些共同的状态，则这些功能状态可以被测试ti确定，也就是说测试ti取值r时可以确定这些功能状态组合，那么，可确定的组合功能状态集表示为

(5)

可以证明Hs(ti)⊆Hcs(ti)。设smk∈Hs(ti)，φi(gim,…,gmk,gjn)=r，则在φi(gik,…,gmx,gjp)=r的集合[gik,…,gmx,gjp]中，必有x=k。这是因为，根据Hs(ti)定义，若x≠k，H(ti|gmk)∩H(ti|gmx)=∅，即与φi(gik,…,gmx,gjp)=r矛盾，因此必有x=k。由此可得smk∈[sik,…,smk,sjp]∩[sik,…,smx,sjp]，进而可以得到Hs(ti)⊆Hcs(ti)。

为了描述测试与测试之间的关系，设RCFtj⊂RCFti，说明tj所测试的功能是ti所测试功能的低层级功能，此时测试点ti的测试取值空间可以通过H(tj)进行计算，即

H(ti)=φi-j(gcfk,…,gcfp,H(tj))

(6)

式中：cfk,…,cfp∈RCFi-RCFj，φi-j(·)为测试tj到测试ti的测试结构函数。若H(ti)取某个值时，能够确定H(tj)的取值，则H(ti)能够确定H(tj)取该值时所确定的组合状态；若H(ti)取任何值都不能确定H(tj)的取值，则H(ti)不能够确定H(tj)所确定的组合状态。当测试tj=b∈H(tj)，测试ti=a∈H(ti)能够确定cfk,…,cfp∈RCFi-RCFj中的某些状态，则在测试tj已知情况下，由测试ti所确定的组合功能状态可以表示为

∀a∈H(ti),b∈H(tj)}

(7)

测试集Ts能够确定的组合状态集包括单个测试所能确定的组合状态以及Ts中各个测试联合所能确定的组合状态，实际上对于测试集来说，由测试ti所确定的组合状态只与该测试紧邻的低层级测试有关，因为其低层级测试取值是包括了更低层级测试取值与相关功能状态的结果。因此，测试集Ts所能确定的组合功能状态集可以表示为

(8)

测试结构函数描述了测试与功能状态以及高层功能测试与底层功能测试之间的关系。多状态系统中零件、部件、子系统、系统的功能状态空间是有限离散的，因此通过结构函数能够确定低层零件功能状态与系统功能状态之间的映射关系，从而使系统低层功能状态通过结构函数往高层功能状态传递过程中是收敛的，避免了系统状态空间爆炸的问题。

2.3 测试点选择方法

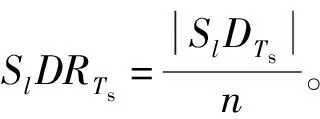
(9)

式中，p(Sl)为系统处于状态组合Sl下的概率。

(10)

式中p(sm0)为功能cfm处于0状态(即故障状态)的概率。

定义系统中与功能cfi相关的测试集RTi={tj|dji=1,tj∈T}，设测试集Ts能够隔离的功能故障集合为FITs，有FITs={cfi|cfi∈FDTs,RTi⊕RTj≠0,∀cfj∈FDTs}。则测试集Ts下，系统的故障隔离率为

(11)

(12)

2.4 MSS测试优化算法

当多状态系统包含元件数量较多时，一般需要较多的测试点以满足系统的测试要求。假设系统中有N个可用测试点，那么根据每个测试点选用与否，系统具有2N个测试组合。因此，当N值较大时，应用枚举法对每一个测试组合进行分析，将变成一个工作量巨大的NP完全问题。有必要采用一种启发式的搜索算法寻找到满足要求的测试组合。

本文以经典遗传算法为例重点说明应用启发式算法求解最佳测试点的过程。种群的选择规则即适应度函数的选择是遗传算法的核心内容。由于故障检测率、故障隔离率、状态检测率以及测试代价在不同的情况下，设计人员可能会有不同的偏重，适应度函数可由下式给出：

f(Ts)=λ1·FDRTs+λ2·FIRTs+λ3·SDRTs

(13)

可通过调整系数λ1、λ2、λ3的取值，分别实现对不同测试指标的偏重。当λ3取值为0时，测试优化仅考虑故障检测率和故障隔离率，与二态系统的测试优化相同。

算法包括如下步骤：

2)产生满足测试代价要求的初始群体。根据步骤1)随机生成一定数量的N位二进制码，使得N位二进制码所代表的相应测试集的测试代价满足CTs≤C*。组成初始群体作为进化的第一代。

3)选择种群个体。根据适应度函数判断个体优劣，具有相同适应度函数的个体以测试代价最小为最优，将种群中制定数目的最差评价个体用相同数目的最优个体取代。

4)交叉和。对选择后的种群中每一对个体以一定的概率交换他们之间的部分染色体，当交换后形成的新个体对相应测试代价满足要求时，用新的个体对代替旧的个体对；如果不满足测试代价要求则保留原来的个体对。对群体中的每一个个体以某一个概率改变其中某一些基因，只有当新的个体满足测试代价要求时，用新的个体取代旧的个体，形成下一代种群。

5)经过步骤3)、4)，判断种群中的最佳个体(适应度函数最大的个体，当适应度函数相同时，取测试代价较小的个体为最佳个体)是否满足用户对故障检测率、故障隔离率、状态检测率要求，或者达到最大进化代数，如果是就找到最优个体并结束，否则转到步骤3)。

3 模型实现与分析

本文所研究方法适用于多状态系统相关可靠性数据已知的情况，而对于系统元件多状态数据未知的系统，存在应用上的限制。在许多工程系统中多状态数据统计结果未知的情况下，本文仅做了理论上的分析。

3.1 算例说明

图3所示为某数据处理系统，该系统包含9个组成单元、15个功能及相应的15个可用测试点。每个功能包含3种状态，即si={0,1,2}，处于每个状态的概率为pi={0.1,0.3,0.6}，其中i∈[1,15]。以每个功能的数据处理能力作为其性能指标，表1列出了每个功能在各状态下的性能。

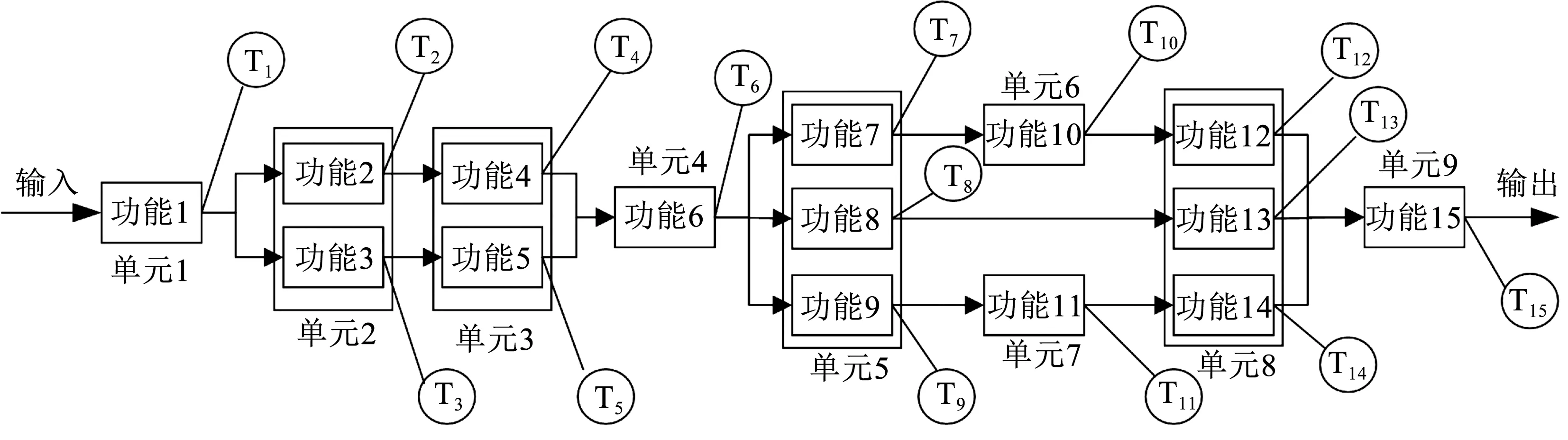
图3 某数据处理系统Fig.3 A data processing system

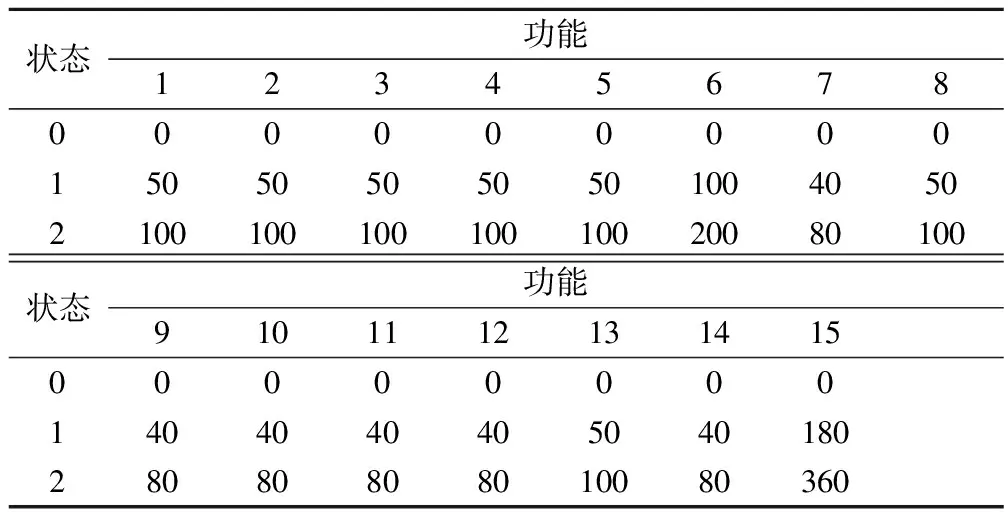
表1 各功能在不同状态下的性能Tab.1 Performance of each function in different states

由系统数据传输特性可知，由式(1)可得系统的结构函数为

V(t)={minG1(t),min[G2(t),G4(t)]+min[G3(t),

G5(t)],G6(t),min[G7(t),G10(t),G12(t)]+

min[G8(t),G13(t)]+[G9(t),G11(t),G14(t)],G15(t)}

(14)

实际应用中的不确定信息是作为已知信息输入的，为了方便计算，这里假定故障的传播及测试是可靠的，可以得到功能-测试依赖关系矩阵为

(15)

由式(2)可得各测试取值空间见表2。

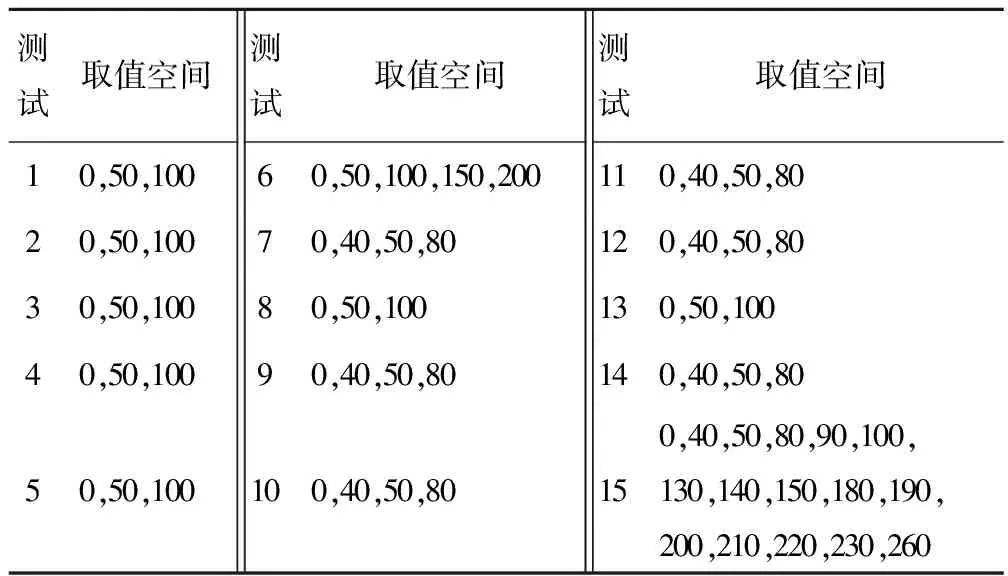
表2 各测试取值空间Tab.2 Value range of each test

由各测试的取值空间及式(4)、(5)得到各测试可确定的状态集及相应测试值见表3。

表3 各测试可确定的状态集及相应取值Tab.3 Detectable state sets of each test and corresponding values

3.2 结果分析

设适应度函数中λ1=λ2=λ3=1/3，各测试点的测试代价为cti=c=1，则对于测试集Ts⊂T，可根据式(9)～(11)分别计算出状态检测率，故障隔离率和故障检测率。根据适应度函数式(13)计算相应测试集的适应度。图4所示为不同测试代价要求下，所求得最佳测试集的测试代价、以及对应的适应度函数值、系统故障检测率、故障隔离率和状态检测率。可以看出，随着测试代价要求的增加，最佳测试集的测试代价不断增加，状态检测率不断增加，最终的FDR和FIR均为1，而SDR未达到1，说明即使选择了所有可用测试点，系统状态也不是完全可知的。

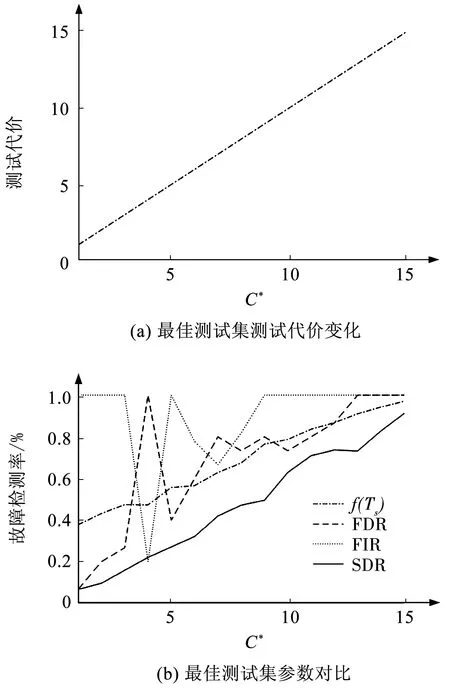
图4 多状态系统各参数随测试代价要求的变化Fig.4 Changes in parameters of multi-state system with test cost

为了对比本文方法所求最佳测试集与二态系统考虑下所求的最佳测试集，设置λ1=λ2=0.5，λ3=0时，此时由于仅考虑了故障检测率和故障隔离率，得到的最佳测试集就是二态系统下的最佳测试集，其在不同测试代价要求下的最佳测试集参数如图5所示。可以看出，系统仅需要12个测试点就能够完全检测并隔离系统故障。随着测试点增多，状态检测率基本呈正增长，而当故障检测率和隔离率逐渐收敛到最大值1后，状态检测率呈现随机波动现象，说明二态系统的测试点选取并没有考虑到状态的测试问题。

图5 二态系统各参数随测试代价要求的变化Fig.5 Changes in parameters of binary system with test cost

表4所示为不同测试代价要求下，考虑多状态系统时应用GA算法得出的最佳测试集及相应参数值。表5所示为不同测试代价要求下，考虑二态系统时应用GA算法得出的最佳测试集及相应参数值。

表4 多状态系统最佳测试集及参数值Tab.4 Optimal test set and parameter values of multi-state system

表5 二态系统下最佳测试集及参数值Tab.5 Optimal test set and parameter values of binary system

通过对比表4、5，可以发现在相同的测试代价限制下，多状态系统的最佳测试集能够获得较高的SDR值，且多状态系统与二态系统的FDR和FIR之和相差不大。对比表4、5的最后一列说明，在测试代价无限制的情况下，本文方法所得的最佳测试集在保证测试性指标(FDR和FIR)的情况下，能够获取更高的系统状态检测率。

4 结 论

1)在分析现有二态系统测试模型基础上，结合多状态系统相关理论，对多状态系统测试性建模方法以及结构、功能和测试的相关描述方法进行了研究，实现了基于结构和功能的多状态系统测试性建模。

2)对状态测试问题进行了分析，并分别对单个测试能够检测的状态集与测试集组合能够检测的状态集的计算方法进行了研究，在此基础上提出了状态检测率的概念实现了退化状态的测试性指标量化。

3)考虑到系统测试性设计与分析中包含故障的测试性问题，因此在多状态系统测试点选取过程中综合考虑了故障检测率、故障隔离率和状态检测率，并提出了测试代价约束下的多状态系统测试点选取方法。

4)考虑到复杂系统测试点较多时，最佳测试集的搜索是一个NP完全问题，因此给出了基于GA算法的启发式最佳测试集搜索方法。应用一个数值案例说明了多状态系统测试建模与测试点选取过程，通过与二态系统测试点选取结果进行对比分析，证明了所提出的方法在系统故障与退化状态测试性分析方面的有效性。