绳系拖拽系统半物理仿真实验装置设计与控制

张世轩，王琬琪，徐志刚，杜木雄，杨明毅

(1.机器人学国家重点实验室(中国科学院沈阳自动化研究所)，沈阳 110016；2.网络化控制系统重点实验室(中国科学院沈阳自动化研究所)，沈阳 110016；3.中国科学院 机器人与智能制造创新研究院，沈阳 110169；4.中国科学院大学计算机科学与技术学院，北京 100049；5.华北计算机系统工程研究所，北京 100083)

随着空间科学的不断发展[1]，航天设备不断被送入太空，越来越多的废弃航天器停留在轨道上形成了空间垃圾，导致服役航天器与废弃航天器撞击的概率逐渐增加。2009年，美国的“铱-33” 移动通信卫星与俄罗斯已废弃的“宇宙-2251”军用通信卫星在西伯利亚北部上空相撞，引发了如何处理废弃卫星的问题[2-4]。清除地球静止轨道空间碎片[5]不但可以降低卫星相撞事故的概率，还可以节省宝贵的轨道位置资源，为今后的发展提供更多可能[6-8]。

针对空间碎片移除问题，Starke等[9]提出通过飞网和飞爪系统抓获废弃航天器碎片，并利用绳索拖拽离轨的ROGER系统，并对两种方案进行了分析。赵国伟等[10]考虑了收集飞行器与废弃飞行器的姿态运动以及系统组合体的整体运动，建立了绳系拖拽离轨系统动力学模型，分析了摆动特性与平稳控制。朱仁璋等[11]则讨论了稳定状态下绳系系统的运动中心及相关力学问题，确定了运动中心在绳系上的位置，并导出了绳系拉力的表达式。王东科等[12]则针对空间绳系机器人对目标抓捕后的复合体姿态稳定控制问题进行了研究，分析了绳系连接到目标后，由于自旋和碰撞所带来的姿态不稳定问题。

考虑到太空实验的成本和难点，大量有关全物理仿真实验、半物理仿真实验的研究逐步开展。文献[13]利用气浮台来仿真卫星在外层空间的低摩擦运动；文献[14]基于滑台式气浮台,采用回转中心与质心重合方法解决了气浮台力矩平衡难题；文献[15]以单轴气浮台作为卫星刚性主体，进行了大型挠性结构卫星全物理仿真试验的研究。全物理仿真可以将大型实物，或者较难实物试验的装置进行等效仿真试验。文献[16]利用物理建模的思想,用SimMechanics建立了空间对接地面半物理仿真台的机械系统,用Matlab/Simulink建立了控制系统模型,搭建了虚拟空间对接地面半物理仿真台，验证了试验的可行性；文献[17]基于dSPACE实时仿真机、单轴气浮转台、星载计算机及陀螺和反作用飞轮的卫星姿态控制系统，设计了半物理仿真，并对仅用反作用飞轮的卫星姿态大角度机动控制模式进行了半物理仿真验证；文献[18]针对对接机构地面测试的空间对接半物理仿真系统，提出系统的动力学解算方案，构建动力学仿真大回路,着重对大回路仿真系统的稳定性进行分析。在航天工程中，半物理实验常常结合全物理仿真与实物进行试验[19]，进行更加可靠的可行性验证。

考虑到回收拖拽过程中系绳中张力测量误差以及等效误差，本文通过半物理实验的方法，对系绳拖拽过程进行仿真验证，进行了一种绳系卫星拖拽系统的地面半物理实验。首先，设计了由半物理仿真单元和全物理加载单元组成的机械结构，分析了等效误差；然后，基于绳系卫星拖拽动力学模型，考虑到实际试验过程中存在的张力测量误差扰动，设计了基于模型预测的控制策略；最后通过仿真，验证了基于所提控制策略的试验响应误差不大于5%，张力误差不大于5%，验证了半物理实验装置的可行性。

1 绳系卫星半物理机械系统设计

1.1 绳系拖拽过程动力学建模

废星绳系拖动控制动力学模型原理如图1所示。

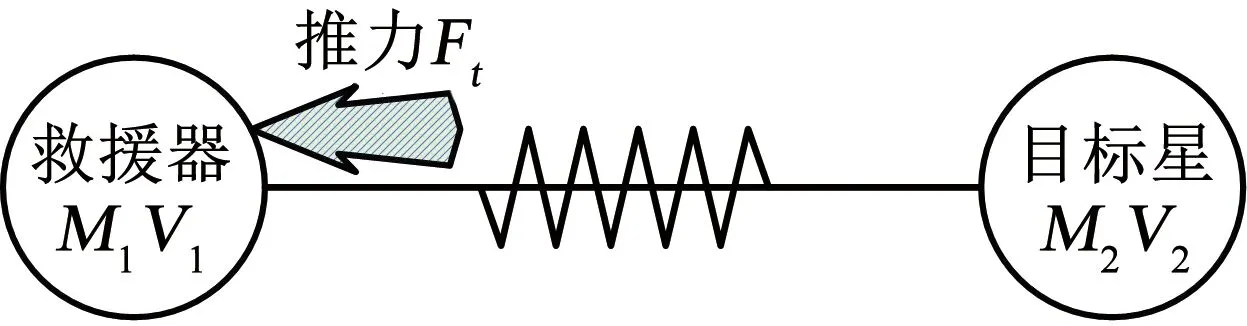
图1 绳系拖动控制动力学模型原理Fig.1 Principle of dynamic model of dragging control

(1)

(2)

(3)

(4)

(5)

实验中全物理仿真单元通过飞轮配重等效惯量实现被动加载功能，等效卫星质量；半物理仿真单元模拟目标在绳系拖拽作用下的动力学状态，测量绳系张力作为输入，实时计算不同平台质量和绳系长度下收放过程载荷，整体半物理装置如图2所示。

图2 绳系半物理系统组成图Fig.2 Tethered semi-physical system composition

1.2 全物理仿真单元等效原理及机构设计

全物理仿真单元用于被动模式下对绳系收放试验产品进行加载测试，具备全物理负载模拟与绳系卷绕等功能。其结构如图3所示。

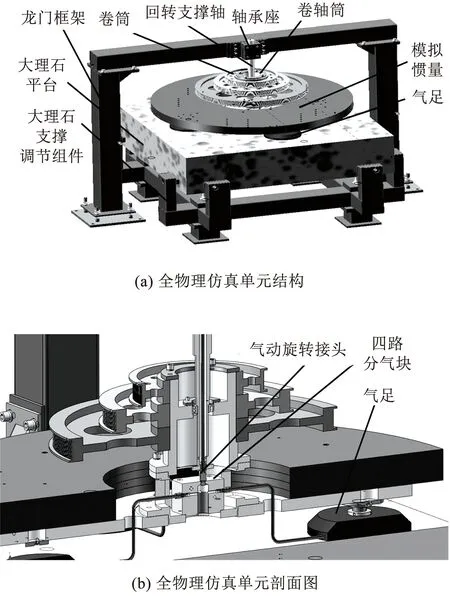
图3 全物理仿真单元机构Fig.3 Full physical simulation unit mechanism

大理石平台通过支撑调整组件安装于地面，通过气源气体节流后形成的承载气膜实现运动组件低摩擦的漂浮于大理石平台上。卷筒用于卷绕绳系，卷筒轴固定于卷筒上，与回转支撑轴通过调心球轴承实现低摩擦转动。惯量盘为全物理加载的模拟负载，其转动惯量模拟空间卫星等效质量。

为保证全物理仿真单元负载模拟的有效性和准确性，对全物理加载单元负载等效模拟进行计算。设全物理试验系统的传动效率为η，惯量盘的转动惯量和角速度分别为Js和ωs，卷筒转动惯量、直径和角速度分别为Jr、Dr和ωr，卫星等效质量为Ms，则通过等效原理可得

(6)

将上式整理可得

(7)

当星体等效质量Ms=500 kg、传动效率η=0.99、模拟转动惯量为40～260 kg·m2(其中气足安装板、气足及其他运动组件转动惯量为40 kg·m2)时，惯量盘的最大角速度为16.80 r/min。

同理，当星体等效质量为Ms=2 000 kg时，模拟转动惯量为220 kg·m2，其他不变时，惯量盘的角速度为13.18 r/min。则通过计算可得，在最大等效质量模拟工况下，惯量盘的最大直径为725 mm。

通过对等效质量模拟的极限情况分析可得，能够进行等效模拟的卫星的质量范围为：290～3 100 kg，相应的模拟惯量的旋转角速度范围分别为1.33～1.76 rad/s，经过换算得到角速度的表示方法为：76.4～100.8°/s和12.7～16.8 r/min。

1.3 半物理仿真单元设计及误差估计

半物理加载单元主要由支撑基座、绳系累计收放长度测量单元、绳系张力测量单元、张力控制单元、卷扬机构和直线移动单元组成，其结构如图4所示。

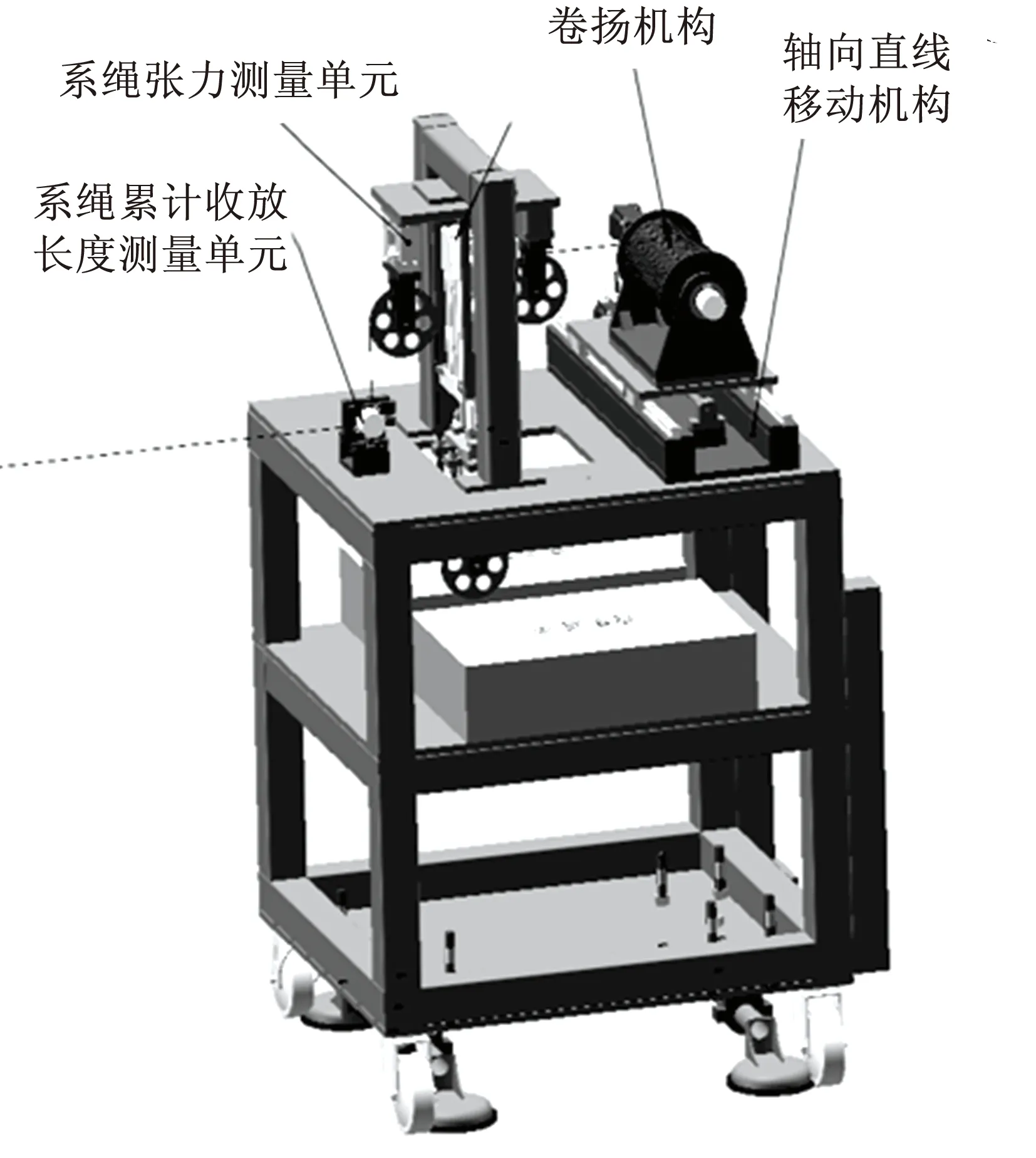
图4 半物理加载单元结构Fig.4 Semi-physical loading unit structure

图4中，半物理加载单元通过基座整体固定于加载单元试验小车上；绳通过绳系收放测量单元测量累计收放长度，并且夹轮组将绳系由水平方向换向至铅锤方向；绳穿过绳系收放长度测量单元后与张力测量单元连接，测量即时绳内张力的大小；绳通过张力测量单元的定滑轮换向后与张力控制单元连接，张力控制单元的电动缸伸缩运动调节绳系中的张力大小，从而实现张力的精确闭环控制。

1.3.1 绳系张力测量单元

绳系张力测量单元用于对绳系张力进行高精度动态测量，其主要由高精度测力传感器和定滑轮组件组成，结构如图5所示。其中，绳穿过定滑轮将运动模式和动力传递给张力控制单元。

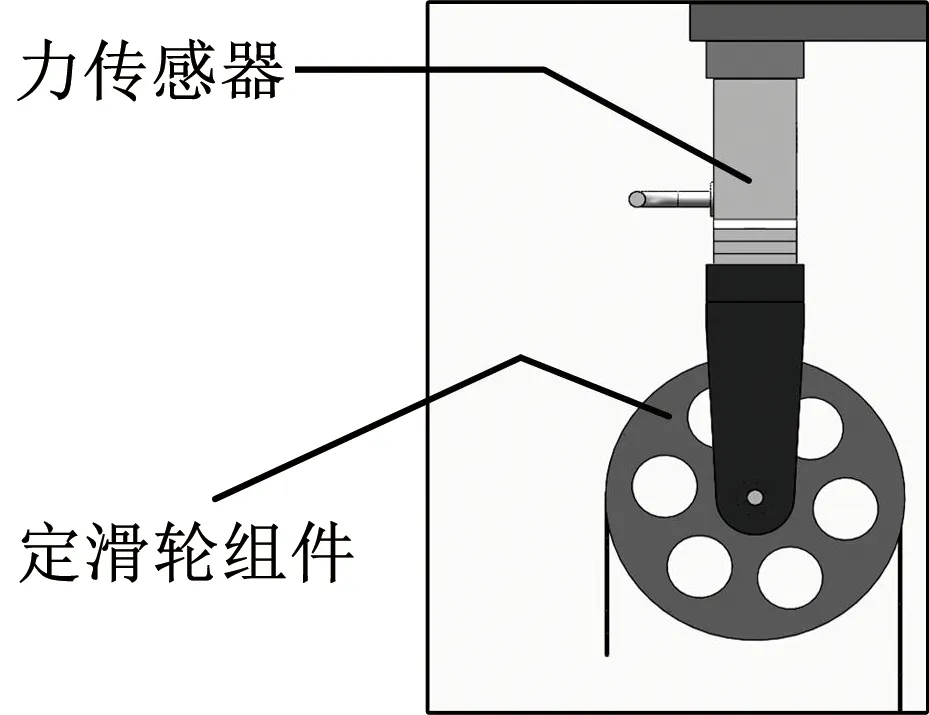
图5 张力测量单元结构Fig.5 Tension measurement unit structure

1.3.2 张力测量误差分析

由于张力测量单元的测量精度受到张力测量传感器误差、滑轮摩擦力和惯量力等因素的影响，张力测量精度要从这三方面去考察。

设收放实验产品绳系的张力为F，通过张力测量单元夹轮组后的张力为F1，通过张力测量单元定滑轮后绳系的张力为F2，张力测量单元的测量误差及张力测量值分别为uF和F′，则根据绳系传递过程可得到：

(8)

F1-F=FI1

(9)

F2-F1=FI2

(10)

式中FI1、FI2分别为绳系长度测量单元夹轮组和张力测量单元定滑轮组引入的惯性力和摩擦力，绳系张力测量表达式如下：

uF=F′-F

(11)

当绳系拖曳力的真值为10 N时，通过式(11)计算得到，张力测量值的误差为0.029 6 N；将大量程张力测量真值(10～50 N)带入式(11)中，可得到张力测量的最大误差为0.3%。

2 绳系卫星半物理仿真控制设计

2.1 控制电机建模

2.1.1 驱动电机模型

驱动电机是扭振系统及加载系统的运动输出执行环节，驱动电机一般由高速小惯量的直流电动机和减速环节等组成。驱动电机在经过减速器后，通过扭矩传感器分别与扭振系统及加载电机连接，驱动电机的模型包括电机开环模型(如图6所示)，PWM驱动器模型及电机常用的速度、电流双闭环模型。

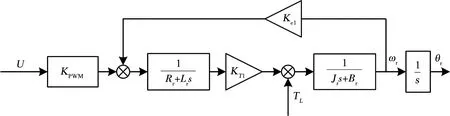
图6 驱动电机开环对象模型Fig.6 Open-loop model of drive motor

2.1.2 开环模型

从系统输入U到输出θr的开环传递函数：

(12)

式中：U为直流伺服电机电枢电压,Rr为直流伺服电机电枢回路总电阻,Lr为直流伺服电机回路总电感,θr为直流伺服电机角位移,Ke1为直流伺服电机反电动势系数,KT1为直流伺服电机转矩系数,Jr为等效转动惯量,Br为直流电机阻尼系数。

2.1.3 PWM驱动环节

PWM脉宽调节装置由脉宽调制器和PWM变换器组成，由于 PWM的变换电压要到下一个周期才能改变，因此PWM脉宽调节装置相当于延时环节。

设PWM脉宽调节装置的开关频率为fPWM，对应的周期TPWM即为延时时间，其传递函数为：

GPWM=KPWMe-TPWMs

(13)

(14)

式中：KPWM为放大系数,ud为PWM变换器的输出电压,uc为脉宽调制器的控制电压。

由于上式中包含指数函数，使得系统为非最小相位系统。为便于分析，将其按泰勒级数展开，则

GPWM=KPWMe-TPVMs=

(15)

由于PWM周期很小，常用的开关频率为10 kHz，因此忽略式(15)中的高阶项，PWM脉宽调节装置近似为一阶惯性环节，其传递函数为

(16)

2.1.4 转速、电流双闭环电机模型

电机采用转速、电流反馈双闭环控制驱动，其闭环数学模型如图7所示。其中KPWM为PWM驱动环节放大系数，TPWM为PWM驱动环节延时周期，Rr为直流伺服电机电枢回路总电阻，Lr为直流伺服电机回路总电感，θr为直流伺服电机角位移，Ke1为直流伺服电机反电动势系数，KT1为直流伺服电机转矩系数，Jr为等效转动惯量，Br为直流电机阻尼系数。

图7 驱动电机闭环对象模型Fig.7 Closed-loop model of drive motor

2.2 位置模式控制

整个系统的控制可以等效为测试加载机构的张力控制和绳系拖拽机构的位置控制实现。张力控制通过力传感器引入张力值与设定值的差值控制绳子中的张力，为位置控制提供输入。位置内环控制器由实际位置、张力测得位置变化值及给定位置三者同时确定输入值。为提高张力控制模式响应速度，系统设计一种基于位置内环的高精度张力控制单元，如图8所示。

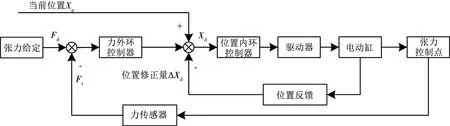
图8 基于位置内环的力控制原理示意图Fig.8 Schematic diagram of force control principle based on inner position loop

基于位置内环的张力控制策略采用用力传感器构建力外环，把力传感器的输出作为内环位置控制器输入的修正值。其控制原理示意图如图8所示，由力传感器测量实际张力Ft，并Ft将与期望力Fd进行比较，经过力外环控制器得到张力系统位置修正量ΔXd，其表达式为

(17)

式中:Kfp、KfI分别为力外环控制的比例和积分系数。从而修正后的位置控制量为

Xd=Xp+ΔXd-Xt

(18)

式中，Xt为位置反馈量，修正后的位置指令为Xd。

由于位置内环控制较为简单，采用PID控制器就可以简单的实现效果较好的稳定。控制律如下：

(19)

2.3 张力模式控制

基于张力控制的精度要求，在静态过程中，简单的PID控制器可以较有效的控制并输出力误差，用于修正位置。然而，在实际拖动过程中，由于张力测量单元的误差，若要使绳内张力始终保持在较小的动态变化中，从而使位置变化量在较小的精度范围内稳定控制，需要用到更复杂的模型预测控制。

模型预测控制采用阶跃响应模型，节省了控制器的设计时间，也同时为动态控制提供了条件。考虑到张力控制系统为SISO的定常稳态系统，通过单位阶跃输入下的输出响应{0,s1,s2,…,sN,sN+1,…}，假设系统N步后达到稳态，则系统输出可以表示为

(20)

式中，Δu(k-l)=u(k-l)-u(k-l-1)。

这样在时刻k就可以预测到未来任意时刻的输出值：

(21)

在控制时域M，预测时域N时，P时刻预测值为

sP-1Δu(k+1|k)+…+sP-M+1Δu(k-M+1|k)

(22)

式中，M≤P≤N。

在张力控制中，设定性能指标为

(23)

式中：ωi、rj都是非负的标量；e(k+i|k)=ys(k+i)-y(k+i|k)为张力误差量；ys(k+i)为未来输出的设定值。式中第1项为最小化张力误差量，第2项为抑制过于剧烈的控制增量，防止张力控制出现震荡造成控制不当。通过最小化性能指标函数J(k)，求解每一步的控制增量Δu，滚动优化到下一时刻中去。这样，由模型预测控制算法所得设计的控制框图如图9所示。

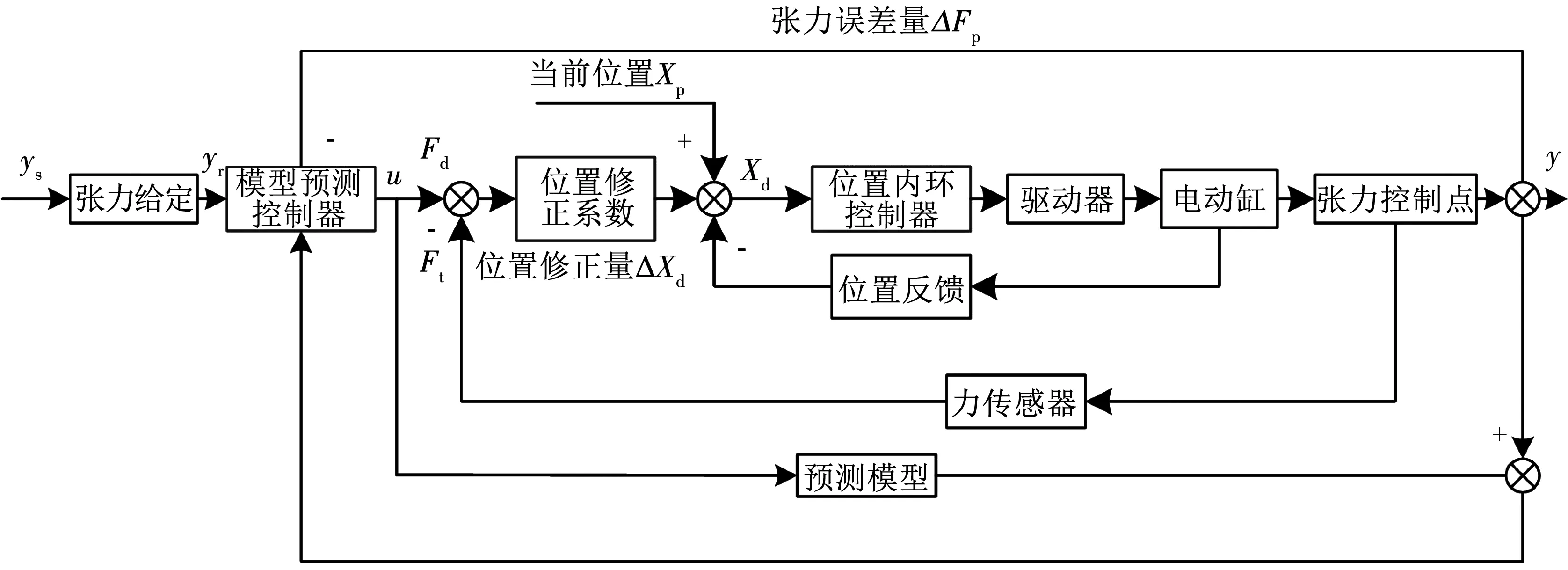
图9 模型预测控制算法框图Fig.9 Block diagram of model predictive control algorithm

2.4 稳定性分析

考虑系统的输入输出，现将系统等效为二阶振荡环节做稳定性分析。

(24)

系统经采样和零阶保持器后的Z传递函数为：

(25)

式中，p1=-2ecos 2πT，p2=e2，e=exp(-2πTs2)。根据张力模式控制中给出的控制率可知，y0(k+j)为k时刻对于Δu(k)=0的原始输出，那么令ai=1-ei(s2sin 2πTi+cos 2πTi)为系统阶跃响应采样值，在不考虑模型失配时可得系统闭环传递函数：

(26)

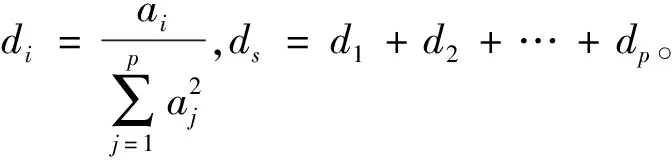
当不考虑控制权时，有下式：

(27)

其中：

根据式(26)、(27)，系统稳定性取决于分母多项式p*(z)的系数，其稳定的充要条件为

(28)

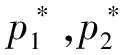
3 仿真校验

3.1 位置模式仿真分析

通过编码器测量输出端位置，利用Simulink搭建仿真模型，调节PID控制器各参数，分析系统频率响应特性及Bode图如图10～12所示。

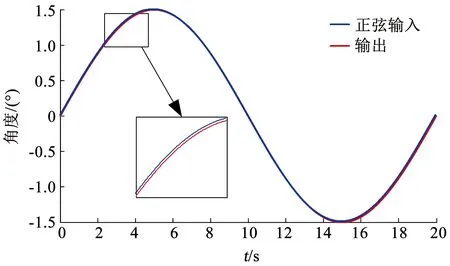
图10 频率0.05 Hz正弦输出响应Fig.10 Sinusoidal output response under 0.05 Hz frequency

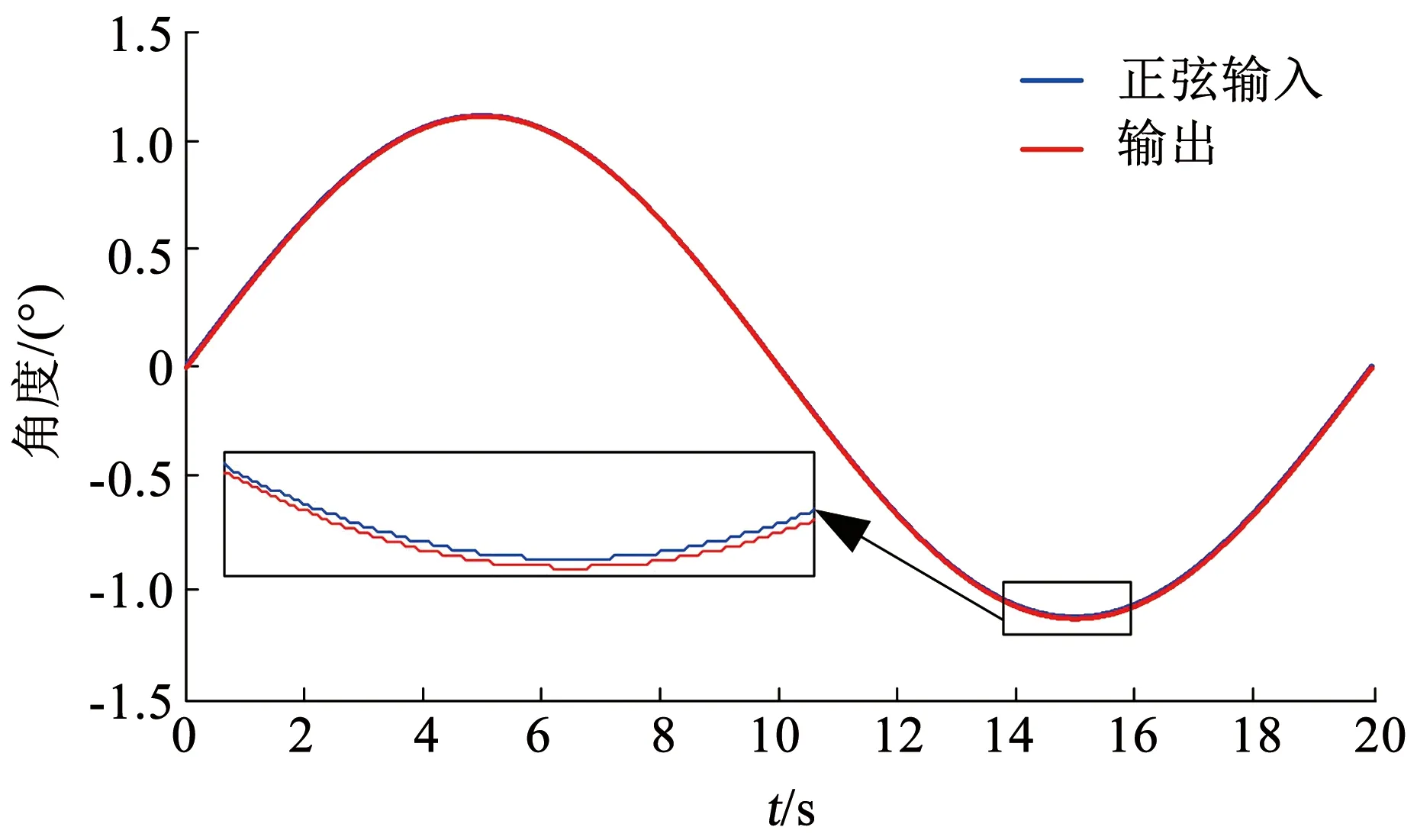
图11 频率0.20 Hz正弦输出响应Fig.11 Sinusoidal output response under 0.20 Hz frequency

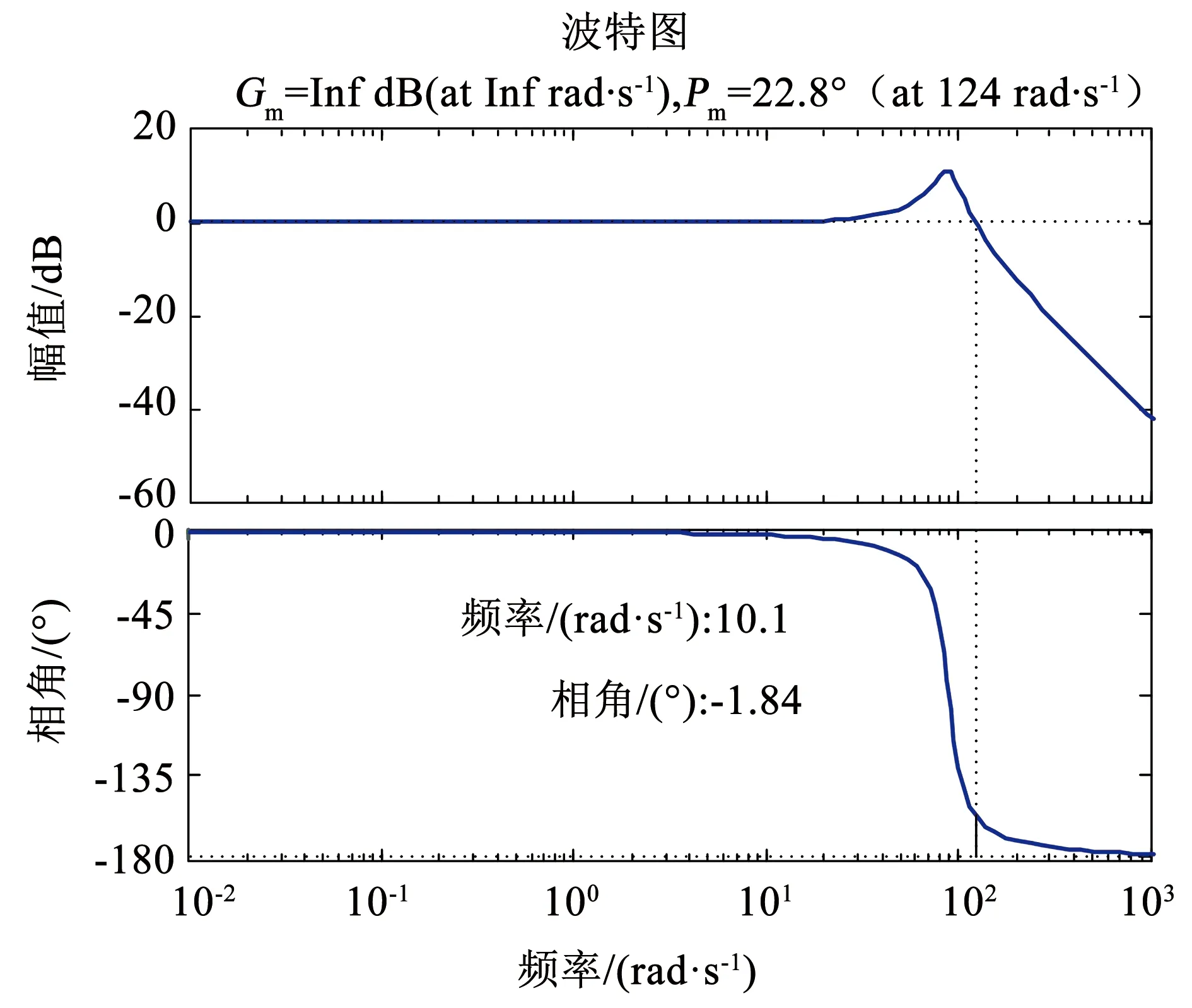
图12 系统带宽响应Fig.12 System bandwidth response

通过正弦跟踪可以看出，通过PID校正，系统的位置模式控制可以达到良好的跟踪效果。系统的相角裕度Pm=22.8°，可以看出系统的稳定的。同时，系统在10 Hz时相角位移为1.84°，系统在10 Hz以内有较好的频率响应特性。

3.2 张力模式仿真分析

外环张力控制时，由于系统仿真救援是一个弹簧系统，拖拽过程中会产生一定频率的误差；同时由于张力测量误差的存在，可将这类干扰视为有界干扰噪声。仿真过程中，在系统输入信号中加入有界随机噪声作为抖动干扰，测试模型预测控制对干扰的抑制作用。可以看到系统频率响应如图13、14所示。

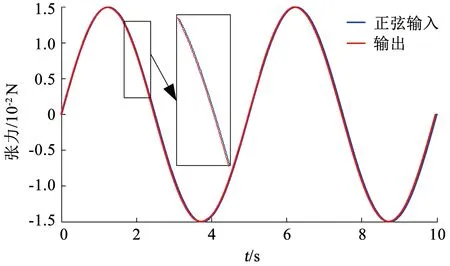
图13 0.05 Hz力载荷输出Fig.13 Force load output under 0.05 Hz

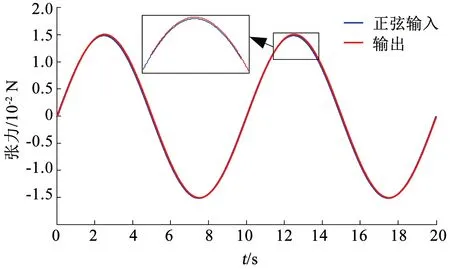
图14 0.20 Hz力载荷输出Fig.14 Force load output under 0.20 Hz

3.3 模型预测控制控制器仿真

模型预测控制器设计中，采样间隔取0.4 s，预测时域长度为30 s，控制时域长度取10 s，输入权重为0.3，输出权重为1.0，暂不考虑绳系抖动因素，不加入约束条件。则控制器设定时相关参数曲线如图15所示。

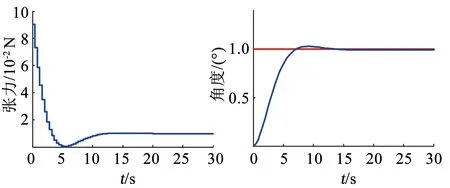
图15 预测控制控制器信号及阶跃输出曲线Fig.15 Model predictive control signal curve and step response curve

可以看出，通过设计模型预测控制器，即使加入了噪声信号，如图16所示，频率响应曲线仍可以较好的跟踪输入，为力误差反馈提供了较好的条件。

图16 加入噪声后的0.20 Hz力载荷输出Fig.16 Force load output with noise under 0.20 Hz

3.4 误差分析

通过实验测量，得到如图17、18所示张力误差曲线及联合电机阶跃响应曲线。可以看出，在实际工况中，力误差降低到了需求的5%以内，响应曲线也可以较好的满足试验要求。

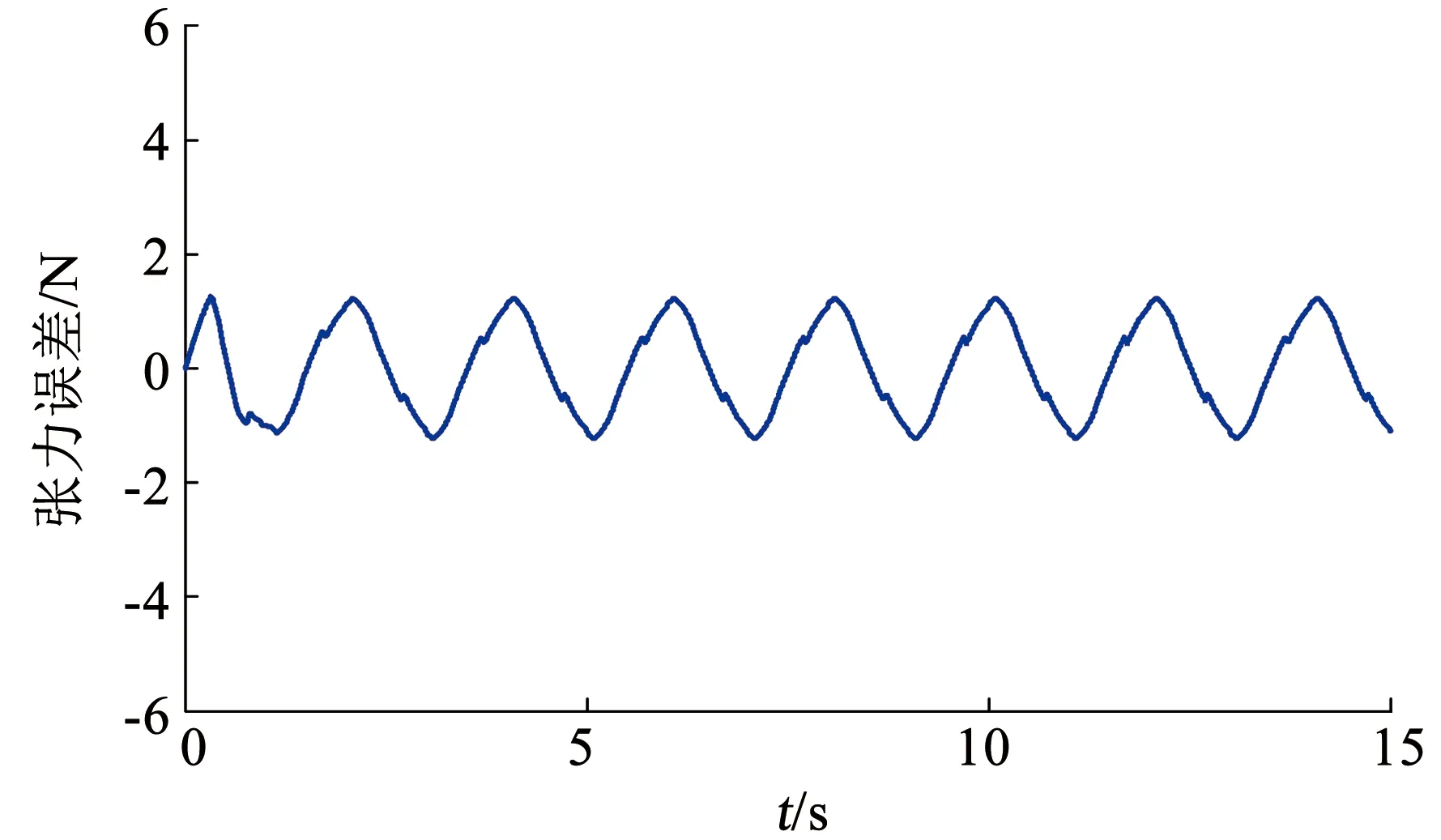
图17 0.20 Hz频率响应下张力误差曲线Fig.17 Tension error curve under 0.20 Hz frequency response

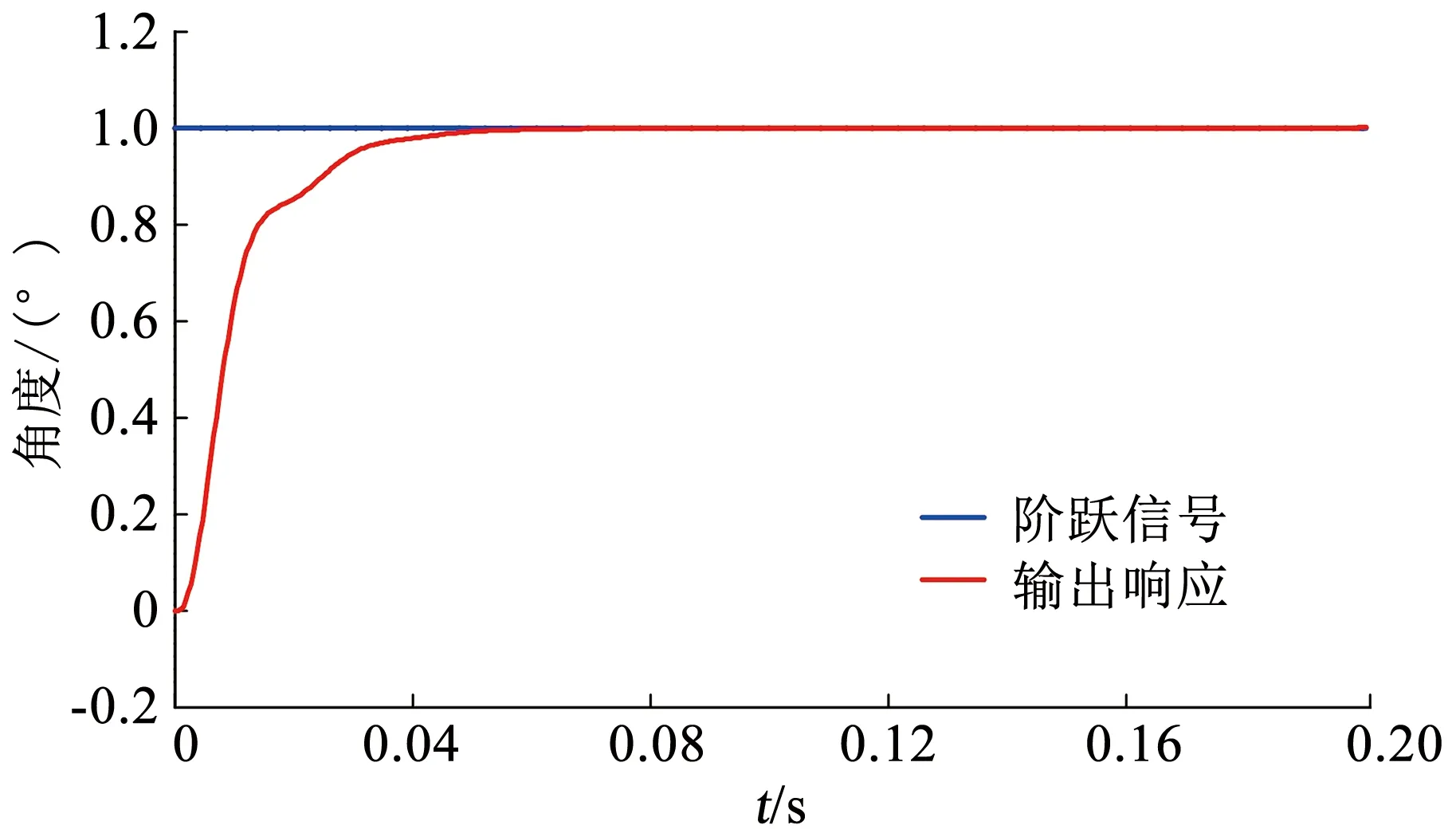
图18 联合电机阶跃响应曲线Fig.18 Combined motor step response curve

4 结 论

1)本文针对空间废弃卫星绳系系统的回收过程，采用半物理仿真实验技术设计了一种地面仿真实验装置。通过对绳系拖拽过程进行动力学建模，设计了实验装置。实验装置分为全物理加载单元和半物理仿真单元，分别用来模拟卫星等效质量和卫星在绳系拖拽作用下的动力学状态。通过对两部分实验装置的参数分析和误差估计，实现了绳系拖拽系统的机械设计。

2)为解决绳系拖拽半物理仿真实验的控制问题，建立了基于伺服系统的双电机模型。针对绳系拖拽系统的验证问题，将整个系统的控制等效为了测试加载机构的张力控制和绳系拖拽机构的位置控制，通过双闭环电机的仿真实验，验证了所设计控制系统的良好频率响应特性。

3)考虑到实际绳系拖拽过程中会出现的张力测量误差扰动，通过将张力控制性能指标设为优化函数，并进行稳定性分析，设计了可抑制扰动的模型预测控制控制器。通过等效张力误差为有界干扰噪声的方法，进行了一组仿真验证。仿真结果表明，力误差降低到了需求的5%以内，实现了较好的控制效果。