基于非线性混合效应模型分析兽药药代动力学研究进展
王建中,苏富琴,曹兴元
(1.山西农业大学动物医学学院,山西太谷 030801;2.中国兽医药品监察所,北京 100081;3.中国农业大学动物医学院,北京 100193)
兽药临床药代动力学常用数学模型分析药代动力学数据。随着分析化学技术和计算机数据分析科学快速发展,兽药药代动力学研究的复杂性也在逐渐演变[1]。传统药代动力学(Pharmacokinetics,PK)仅关注基于药代动力学参数的生理学参数,或者仅限于经典房室/非房室模型的论述。如传统药动学模型是由数据驱动的模型,其模型结构由具体参数决定的经验性模型;传统药动学模型是将浓度随时间的变化拟合为吸收、分布、代谢和消除的速率相关一系列指数项;其模型参数没有具体解剖学和生理学含义,只是简单描述以获得数据,无法外推至另一组数据。另外一种常见的分析方法,非房室模型是以概率论和数理统计学中的统计矩方法为理论基础分析相关数据,包括零间矩、一阶矩和二阶矩。最终使用整体随机变量的平均值/中值和标准值等概念体现药代动力学参数,试验设计方面需要尽量避免潜在因素影响(如协变量:动物品种、体重、年龄、疾病状态等),试验样本的同质性要求高。
随着药物检测分析技术精准量化机体内药物含量以及计算机数据分析技术的快速发展,药代动力学研究者能够计算出更精确和复杂的药代动力学模型[2]。上世纪八十年代开始,药代动力学研究者逐渐关注药动学-药效学(Pharmacokinetic(PK)-pharmacodynamic(PD), PK-PD)推理、混合效应和基于生理学的药动学模型(Physiological-based pharmacokinetic,PBPK)[3-4]。PK-PD建模则从一个描述性学科演变为使用体外和动物体内的数据预测人体内药物暴露量和作用效果转化医学科学。此外,毒代动力学学科的发展,促使一些有争议的数据、物种差异、非线性消除和二进制(有毒和无毒)来进行剂量外推[5]。近年来,数学建模和模拟等跨学科和产业研究的投入加大,加快了药物的研发进程[6]。新药研发在3R原则下建模与模拟不可或缺,在许多新药申请评价中建模与模拟已经被美国FDA接受。调查2000-2008年198份FDA新药申请案例,约70%新药申请由FDA定量药理学(非线性混合效应模型分析)部门评价,可见基于模型分析在评价药物中的作用[7]。基于非线性混合效应模型分析药代动力学的方法为新药研发策略制定以及监管部门科学评价与监管提供关键依据,逐渐成为新药研发不可或缺的研究内容[8]。美国、欧盟、日本和中国的药物管理机构先后发布了群体药代动力学的相关指导文件。美国FDA于1999年首次发表并于2019年更新了群体药代动力学研究指南[9-10]。欧洲药监局于2011年成立了建模与模拟工作组评价新药申请中有关定量药理学内容[11]。日本药品与医疗器械管理局也于2019年发布了群体药动学分析指南[12]。国家药品监督管理局(CDE)为鼓励和引导数学建模与模拟在新药研发与评价中的应用,先后在2005年发布《化学药物临床药代动力学研究技术指导原则》、2020年《模型引导的药物研发技术指导原则》和2021年《群体药代动力学研究技术指导原则》相关指导文件[13-15]。我国CDE的相关专家一直紧盯国际科研前沿,紧跟新药研发模式。在兽医领域,尽管欧洲兽医药理学联合学院院长,西班牙皇家兽医科学院外籍院士,法国图卢兹国立兽医大学著名的Toutain教授一直致力于兽药药动学的研究,但是兽药动态动力学(kinetic-dynamic)理论和应用研究的增长相对较慢。
兽药临床药物药代动力学在靶动物中(不同品种、体重、年龄、性别、病理生理状态、饲喂前/饲喂后等)变异对后续新兽药研发以及药物上市后临床安全使用和监管极为重要。评估兽药药代动力学在靶动物群体中变异,对提高药物疗效和安全性具有重要意义。传统药代动力学技术研究忽略了建模技术实践和演绎。基于非线性混合效应模型的定量药理学能够重点针对动物机体不同协变量(动物品种、体重、年龄、性别、病理生理状态、饲喂前/饲喂后等)的药代动力学与药效学数据进行建模与模拟,形成有别于生物统计学的另一种模型化数据分析法和定量设计法[16]。
1 非线性混合效应模型概念
非线性混合效应模型(Nonlinear Mixed-effects Modes, NLME)是基于动力学和动态学的一体化描述药物代谢和/或药理学反应模型,根据患病动物特征(协变量)定量分析药物代谢和药效反应,统计学分析动物个体内和个体间以及试验间差异。
“非线性(nonlinear)”指因变量(如浓度)与模型参数和自变量是非线性关系。“混合效应(mixed-effects)”是指参数化,主要有固定效应(fixed effects)和随机效应(random effects),其中固定效应是不随个体变化的参数,随机效应指随个体变化的参数。建立群体药动学模型主要五个方面:(i)数据,(ii)结构模型,(iii)统计学模型,(iv)协变量模型和(v)建模软件。群体药动学模型包含三个子模型:结构模型、统计学模型和协变量模型。结构模型是描述群体内典型的浓度时间过程,用固定效应参数描述数据整体走势。统计学模型是用来解释群体内浓度“无法解释”的变异(如个体间变异、不同试验、残差变异等)。协变量模型解释由个体特征(协变量)预测的变异,即协变量和模型参数的关系。非线性混合效应建模软件将数据和模型结合在一起,最终确定描述数据的结构模型、统计学模型和协变量模型参数[17]。非线性混合效应模型的原理示意图如下(图1)[18]。

图1 非线性混合效应模型的原理示意图[18]
非线性混合效应模型主要是鉴别和定量靶动物群体中的药动学参数变异来源。其优点不仅可以每个个体取样少,并且多个体(或组别)也可同时纳入研究,以及将影响药物代谢和/或药理学作用的协变量(如性别,年龄,体重和肌酐水平和其它生物指标变量)都可被鉴别和整合到模型。此外,模型不仅可以处理稀疏数据,也可处理密集数据[5]。同时,非线性混合效应模型也可将临床前研究获得的数据应用到个性化给药(如患肿瘤宠物精准给药和优化抗生素优化临床给药剂量等)[19]。
2 非线性混合效应模型建模原理
Sheiner and Ludden分别在1977和1992年提出了非线性混合效应模型概念[18],由如下公式表示:DV=IPRED+εij。公式中,IPRED=PRED+ni;IPRED=F(φi,tij)φi=μ+ni; DV(Observations)表示第i个个体在tij时刻的观察变量(如:血药浓度);PRED(Populations Predictions):群体预测值;IPRED(Individual Predictions):个体预测值表示某个体在tij时刻参数为φi时的观察变量的值;
个体数学(随机)模型由公式表示:IRRED=yij=F(Dose,φi,tij)+G(Dose,φi,tij,β)·εij,F(Dose,φi,tij)是药动学参数为φi,tij时刻的个体观察值;G(Dose,φi,tij,β)是测量误差在tij时刻的标偏差;群体药动学模型中F(Dose,φi,tij)称为结构模型;G(Dose,φi,tij,β)表示残差模型;φi表示个体参数的向量(如:kai,Cli,Vdi);个体参数φi的变异来源由群体特征(如协变量)来解释。φi=μ·eηi,μ是模型参数的典型值(如kapop,Clpop,Vdpop)。
εij独立的随机变量,表示误差(个体内/实验间的变异);随机变量εij以0为中心,分别以σ2标准差的正态分布或lognormal分布,标记为ε(0,σ2)。
ni:独立的随机变量,表示个体参数φi与中值μ之间无法阐明的差异(个体间随机变异)。随机变量 以0为中心,以ω2标准差的正态分布或lognormal分布,标记为(0,ω2)。随机变量εij和ni是0为中心,分别以σ2和ω2为标准差的正态分布。DV和φi通常是正态分布或lognormal分布。
3 非线性混合效应模型的评估
模型基于最大似然函数(SAEM)算法评价非线性混合效应模型中固定效应和随机效应参数。拟合优度(Good-of-fit,GOF)诊断个体预测vs观察值,加权残差分布(Distributions of Weighted Residuals,IWRES)和正态分布预测误差(Normalized Prediction Distribution Errors,NPDE)等指标评价最优和最合适模型。蒙特卡洛模拟(Monte Carlo Simulations)评价最终模型重现观察药动学参数的变异性。使用直方图、分位图(Quantile-Quantile Plots,Q-Q)、权重残差等条件性分布相关性评价残差条件性和正态性。拟合的模型都是基于贝叶斯信息标准(Bayesian Information Criteria, BIC)和精确的模型参数估值评价。BIC根据AIC(Akaike Information Criterion),选择最简单最准确模型[20]。
4 非线性混合效应模型分析在兽医临床研究进展
目前,NLME在兽药领域未被充分应用。NLME的建模最初分析人用窄治疗窗药物寻找最佳临床治疗剂量。NLME特别对个体间变异大或者药动学参数受疾病和药物本身等影响较大的药物评价有着不可替代作用[21]。由于NLME仅需较少血浆样品或数据(稀疏数据)即可建模和模拟[22],近年来逐渐被兽医药理学家用来探索年龄、性别和疾病状态等协变量对药动学影响[23]。
Martin-Jimenez 和 Riviere(1998)[23]首次应用NLME模型分析监测庆大霉素在马体内药动学,发现庆大霉素在马体内的药动学参数变异60-70%来自体重和血清肌酸酐浓度。当动物个体之间变异性较大时(品种、体重、年龄、性别、病理生理状态、饲喂前/饲喂后等),NLME模型可根据采取蒙卡特罗模拟整合药动学参数、细菌敏感性和靶位点计算抗菌药物最佳给药剂量,并根据各种协变量如体重、肝脏或肾脏功能调整剂量,减少药物过度暴露危害(或治疗失败)。Sheiner等[24]在1977年使用NLME分析了影响地高辛在人体内分布和清除的因素。20年之后,Whittem等[25]研究分析地高辛在全体内分布和清除因素,发现犬存在两个亚群导致地高辛的吸收速率有十倍的差异,住院给药的犬比居家给药的犬会明显推迟地高辛的吸收,可能由于生理应激影响肠道排空。Warrit等[26]通过研究确认住院给药的犬胃排空时间(71.8 h)明显比在家居住犬的时间长(17.6 h)。近来,NLME被应用到许多伴侣动物的治疗适应症(如心脏疾病和疼痛)。Mochel等研究肾素-血管紧张素-醛固酮体系、血压和尿液电解质的时间生物学,来探索犬血管紧张素转换酶抑制剂的最佳给药时间[27]。同时Mochel等通过收集稀疏数据和建立PK/PD NLME模型找到最佳的晚上给药方案,研究结果与在人医临床研究一致[28]。
过去十五年,NLME分析的兽医药理学文章陆续发表。NLME分析患骨关节炎犬和猫中NSAIDs的剂量选择和协变量甄别[29-30]。Sliber等[31]研究发现robenacoxib在健康犬中的清除率比在患骨关节炎犬中要高75%。Pelligand等[29]应用NLME模型分析robenacoxib在83只猫体内药动学,评价其痛觉缺失效果和最佳给药剂量[29]。在mavacoxib一项研究中,使用NLME PK模型模拟显示 2 mg/kg的剂量足以维持犬体内的有效浓度,促使官方4~2 mg/kg推荐剂量降低[30]。此外,国外研究者应用NLME研究分析topiramate在患癫痫犬体内药动学[32], tobramycin在马体内药动学[33], 青霉素G在牛和猪体内药动学[34]等。
笔者应用NLME模型分析选择性COX-2非甾体抗炎药维他昔布片在犬和猫体内的药动学特征,分别建立维他昔布在犬和猫体内的非线性混合效应模型,发现体重影响模型的中央室体积(V1):log(V1i)=log(V1pop)+βV1WT0·WT0i+ηV1i(其中,V1pop为中央室分布容积的群体典型值,βV1WT0为体重对V1影响效应,WT0i为个体体重,ηV1i个体随机效应),应用非线性混合效应模型和维他昔布片对环氧化酶(COX-1和COX-2)药效学试验结果(IC80/20),结合PKPD模型理论蒙特卡洛模拟优化了给药剂量并应用模型评价和模拟最优给药剂量(如图2)[35-36]。此外,笔者应用非线性混合效应模型发现头孢噻夫钠在药动学特征有雌雄差异(图3),并应用蒙特卡洛模型模拟不同给药剂量和给药间隔(图4)研究头孢噻夫钠在犬体内药动学[37]。

图2 非线性混合效应模型药动药效学联合模型蒙特卡洛模拟不同给药剂量维他昔布对猫COX-1(IC10& IC20)和COX-2(IC80& IC90)的时间-有效血药浓度关系图[35, 36]
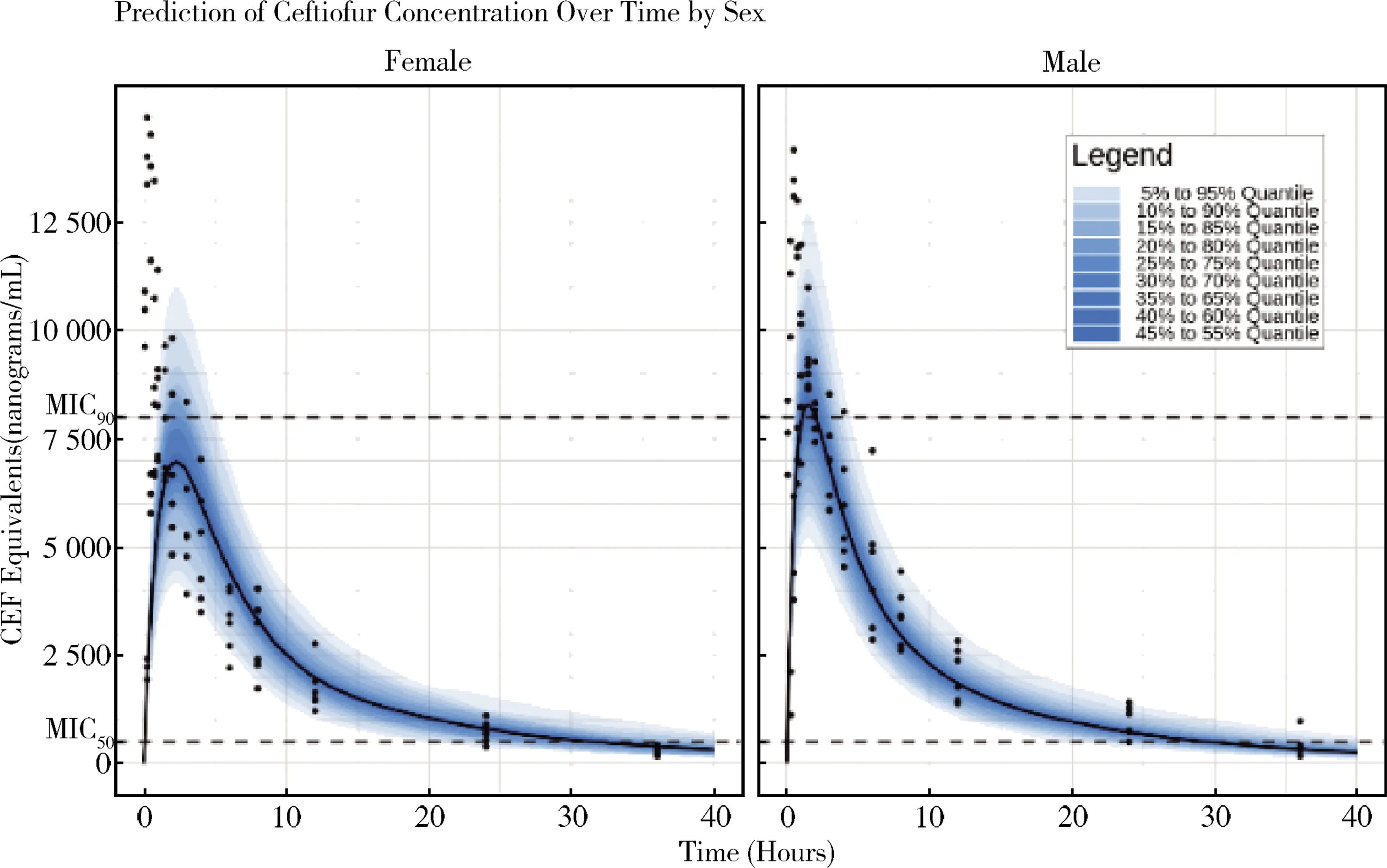
图3 头孢噻夫钠在健康比格犬内的药动学(左:雌性犬;右:雄性犬;虚线为头孢噻夫钠对呼吸道分离的大肠杆菌MIC90[37]

图4 基于非线性混合效应药动药效学联合模型蒙特卡洛模拟的不同给药剂量有效浓度持续时间(左:雌性犬;右:雄性犬)[37]
5 结 语
随着我国兽药企业自主研发水平不断提高,新批准的化药一类新兽药逐渐增多,如喹烯酮(2003)、紫锥菊(2012)、维他昔布(2016)、沙咪珠利(2020)等。非线性混合效应模型在新药研发与评价阶段的应用将对企业高效的研发与药物评价、及临床科学安全合理用药,特别是根据临床靶动物群体的不同点,优化抗菌药物临床给药剂量,防治细菌耐药性等具有重要意义。

