考虑AGC调节大容量风电波动性的机组优化调度

周博然，尚 洁，王 琪，冷传珏

(1.国网大连供电公司，辽宁 大连 116001；2.中国农业银行大连市分行甘井子支行，辽宁 大连 116021)

电力系统调度由机组组合(unit commitment，UC)、经济调度(economic dispatch，ED)和自动发电控制(AGC)相互衔接,构成了基本调度运行框架,为电网的安全稳定提供了可靠的保障[1]。其中UC作为3种方法中时间尺度最长的问题，其优化的结果直接影响接下来的ED和AGC。因此UC结果对电力系统的安全稳定起着重要的作用。

传统的UC模型不考虑其与经济调度之间的衔接关系，即不考虑网络的安全约束。为了更好的衔接UC与ED，网络安全约束被加入到UC中，建立安全约束机组组合(security-constrained unit commitment，SCUC)模型，增强UC结果在实际中的可行性。SCUC模型较好的衔接了UC与ED，但是SCUC模型中没有考虑UC与AGC之间存在的衔接关系。近年来随着风力发电大量接入电网，其出力调节性差、变化速度快、预测误差大等特性给电网运行调度带来了新挑战。AGC作为一种快速调节系统功率平衡的手段，在应对风电出力快速变化造成系统功率不平衡问题上发挥重要的作用。AGC相关约束一般单独考虑而不在UC中考虑。当AGC需求容量不大时，通过重新调度现有在线机组，可以满足系统需求。随着风电大规模接入，系统的波动性显著增大，AGC需求也在增大。如果在UC中不考虑AGC约束，很可能出现在线运行机组无法满足AGC需求或者需要大幅度调整在线机组出力而增加运行费用的情况。因此，本文将UC与AGC之间的衔接关系以约束的形式添加到UC模型之中，提出了考虑AGC调节的安全约束机组组合模型(AGC-SCUC)，使用Benders分解方法，减小计算规模，加快计算速度，有效地将机组组合、经济调度和自动发电控制之间的衔接关系通过约束条件表达，增强机组组合结果的实际可行性和经济性。

1 机组组合模型

1.1 考虑AGC约束的机组组合模型

AGC-SCUC模型优化的目标函数为

(1)

式中：Nt为总时段数；Ng为发电机数；NAGC为可提供AGC服务机组数；Pi,t为机组i在时刻t的有功出力；Fi为机组i的发电成本函数；STi为机组i的启动费用;CAj为AGC机组j的AGC服务费。

满足以下约束：

a.功率平衡约束

(2)

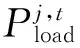
b.系统备用约束

(3)

式中：t=1,2,…，Nt；Pi,max为机组i的有功出力上限；Rt为系统t时刻的备用百分比，Rt设为20%。

c.机组出力上下限约束

Pi,minui,t≤Pi,t≤Pi,maxui,t

(4)

式中：t=1,2,…，Nt；i=1,2,…,Ng；Pi,max、Pi,min分别为机组i的有功出力上、下限。

d.最小启停机约束

(5)

式中：Ti,on为机组i的连续在线时间；Ti,off为机组i的连续离线时间；Ti,up、Ti,down分别为机组i的最小连续在线、离线时间。

e.机组出力爬坡约束

(6)

f.线路潮流约束

(7)

式中：t=1,2,…，Nt；l=1,2,…，NL；NL为线路总数；T为节点有功功率输入对线路的转移分布系数矩阵；FLl为线路l的功率输送上限。

g.AGC容量约束[2]

(8)

(9)

式中：AUj,t为AGC机组j在时刻t的上调容量；ADj,t为AGC机组j在时刻t的下调容量；SUt,SDt为系统时刻t的AGC上下调节容量需求。

h.AGC爬坡速率约束[2]

(10)

(11)

式中：VUj,t，VDj,t为AGC机组j在时刻t的上下爬坡能力；SVUt，SVDt为系统在时刻t的AGC上下爬坡能力最小需求。

将目标函数中的发电成本函数、启动费用函数和约束条件中的最小启停机约束进行线性化。

1.2 AGC约束的线性化表达

假设1台机组可以进行AGC调节，其机组的正常出力上下限为[Pmin,Pmax]，对应的AGC调节出力范围[Amin,Amax]，通常Pmin≤Amin≤Amax≤Pmax，如图1所示。这意味着如果这台机组作为AGC调节机组，其出力范围就要相应缩小为[Amin,Amax]，机组将无法满发。这带来了经济上的损失，因此对参与AGC调节的机组要进行经济补偿，即目标函数(1)中的CA项。本文把每台AGC机组的费用固定为常数，即系统安排1台AGC机组在一个时段参加AGC调节，系统就要补偿给该机组对应的AGC调节费用。AGC容量和爬坡速率约束中的AU,AD,VU,VD相关约束的线性表达式如下：

图1 AGC机组出力范围

Xj,t≤uj,t

(12)

Pj,t≥Pj,minuj,t+(Aj,min-Pj,min)Xj,t

(13)

Pj,t≤Pj,maxuj,t-(Pj,max-Aj,max)Xj,t

对表2 的数据进行分析归纳整理，改进企业领导人员网络培训的意见建议主要有五个方面：一是研究和探索互联网下，干部培训模式变化规律和趋势；二是加快网络培训平台建设，推进移动学习平台；三是资源共建共享（课程资源），搭建共建共享平台；四是现代化教育培训手段和培训方式的应用，培训方式方法创新，探索线上线下混合式教学；五是化解工学矛盾，满足培训需求。

(14)

AUj,t≤Aj,max-Pj,t+(1-Xj,t)Pj,max

(15)

ADj,t≤Pj,t-Aj,min+(1-Xj,t)Aj,min

(16)

AUj,t≤(Aj,max-Aj,min)Xj,t

(17)

ADj,t≤(Aj,max-Aj,min)Xj,t

(18)

VUj,t≤VUPjXj,t

(19)

VUj,t≤Aj,max-Pj,t+(1-Xj,t)Pj,max

(20)

VDj,t≤VDPjXj,t

(21)

(22)

式中：j=1,2,…，NAGC；t=1,2,…，Nt；Xj,t表示AGC机组j在时刻t是否参加AGC调节；Aj,max为AGC机组j的AGC出力上限；Aj,min为AGC机组j的AGC出力下限；VUPj，VDPj分为别AGC机组j的AGC调节的上下爬坡速率限制。

约束(12)保证只有在线运行的AGC机组能进行AGC调节；约束(13)—(14)保证进行AGC调节的机组出力只能在[Amin,Amax]的范围之内；约束(15)—(18)限定了提供AGC服务的机组能提供的容量大小；约束(19)—(22)限制了每台机组提供的AGC爬坡能力大小，至此，所有相关约束均以线性化表达。AGC-SCUC问题可以表示为目标函数为(1)，满足约束(2)—(22)的混合整数线性问题。

2 模型的解法

Benders分解作为一种求解线性规划问题的方法被广泛应用。该方法可以将一个大规模的线性规划问题分解为几个规模相对较小的线性规划问题，从而减轻计算负担，加快计算速度。

根据上述的Benders分解方法，本文的解法整体框架如图2所示。使用Benders分解方法将原问题分解为不考虑网络约束的机组组合问题和网络安全检验两个问题。这种分解方法能有效地减小问题的计算规模，加快问题的计算速度。

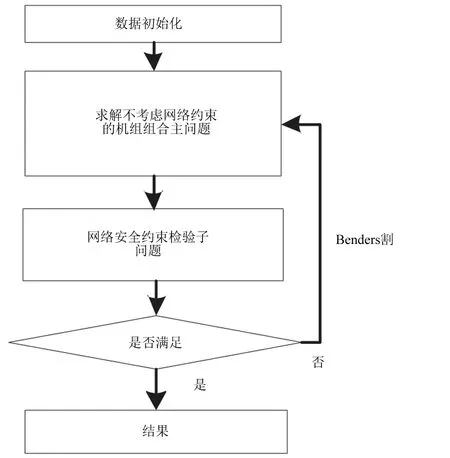
图2 整体解法框架

2.1 不考虑网络约束的机组组合主问题

因为网络约束(7)NL×Nt个不等式约束，约束数量很大，因此在本文在主问题中不考虑网络约束(7)。不考虑网络约束的机组组合主问题的目标函数为方程(1)，约束条件为方程(2)—(6)，(8)—(22)以及由于网络安全约束不能满足时产生Benders割(25)。

2.2 网络安全约束检验子问题

网络安全约束检验子问题实际上是检验上一步的不考虑网络约束的机组组合主问题求出的结果能否满足网络安全约束(7)。这个检验子问题可以表达为一个优化问题，其目标函数为

(23)

满足约束条件：

(24)

如果目标函数(23)的值为0，说明主问题的机组组合结果能满足所有的网络安全约束条件；否则产生Benders割(25)，作为新的约束加入主问题，重新计算主问题。

(25)

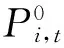
主问题和子问题迭代求解，直到机组组合结果能够满足所有的网络安全约束条件。

3 算例分析

本算例使用IEEE 30节点系统为测试系统，以1 h为1时段，将日前机组组合问题分为24个时段。系统未来24 h的负荷预测值和对应的风力发电预测值如图3所示；机组的特性见表1，机组发电费用F=a·P2+b·P+c；机组的AGC特性见表2，其中机组4不能进行AGC调节。

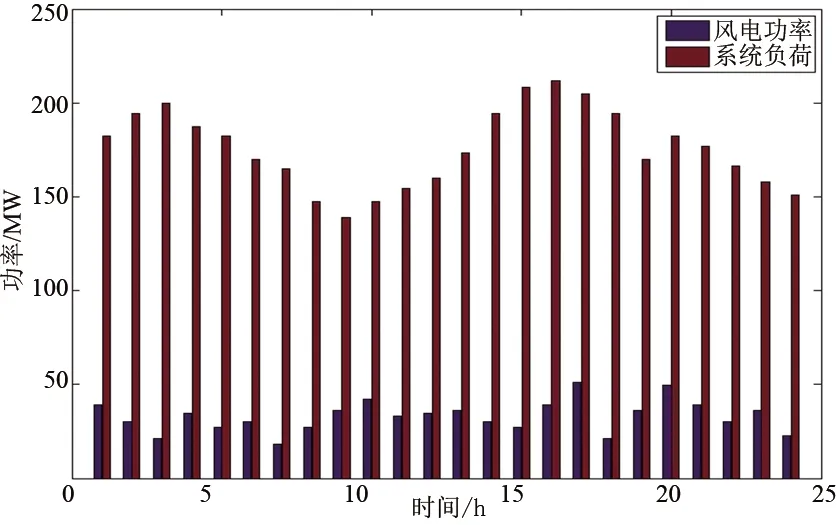
图3 系统负荷与风电出力

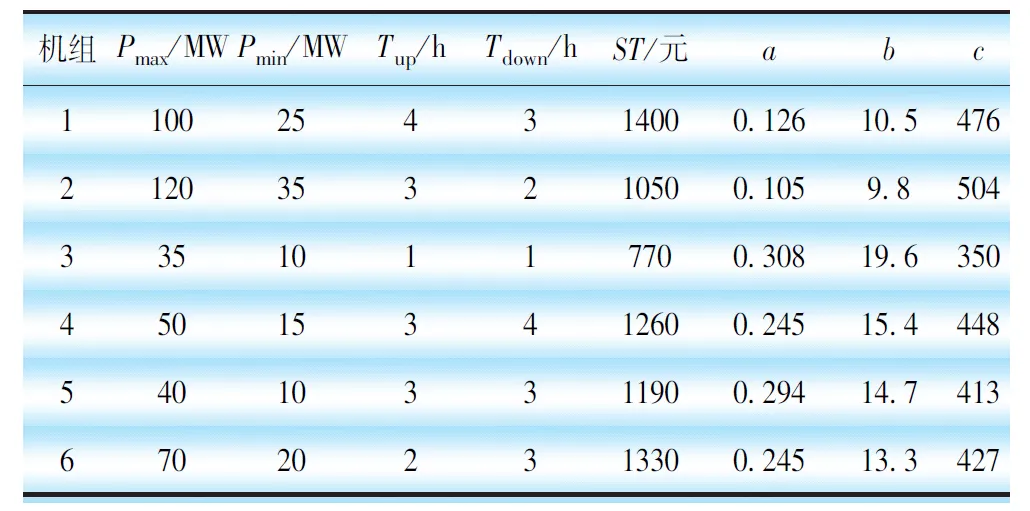
表1 机组特性

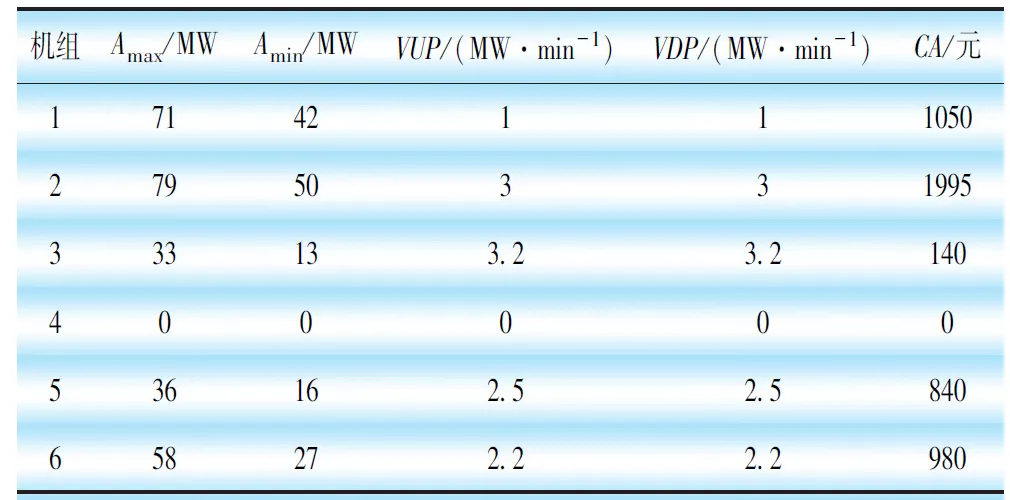
表2 机组AGC特性

3.1 AGC容量约束对于系统的影响

电力系统需要的AGC容量主要受系统负荷的大小以及类型的影响[3]，随着风电的大规模接入，其更强的波动性需要大量的辅助调节手段，因此AGC容量的确定要考虑风电的波动性。参照文献[4]，本文定义电力系统AGC容量需求为式(26)，其中Pwind为系统的风量发电容量，Pload为系统的负荷容量，α为相关系数。

SU=αPwind+0.05Pload

SD=αPwind+0.05Pload

(26)

系统的AGC容量需求受风电的波动性影响，α的取值代表风电的波动范围。下面分别将α取不同值来对比2种模型满足系统AGC容量需求的能力和系统整体经济性，对比结果见表2。

从表2中可以发现，随着系数α的增大，系统的AGC容量需求不断增大，传统的不在机组组合中考虑AGC的UC-ED-AGC模型开始不能通过在线机组AGC重调度满足系统AGC需求，这是因为UC-ED-AGC模型在机组组合阶段没有考虑AGC容量约束，导致安排的在线机组即使改变运行点也无法提供足够的AGC容量满足需求。AGC-SCUC模型由于在机组组合阶段考虑了相关约束，因此一直能满足系统AGC容量需求。从表3中还可以发现，即使UC-ED-AGC模型能满足系统AGC需求，其费用也高于AGC-SCUC模型。其原因可以解释为UC-ED-AGC模型的系统成本优化是分为SCUC和AGC这2个阶段进行的，但是不考虑2个阶段之间的联系，其优化不是从整体进行的，因此其优化结果较差。

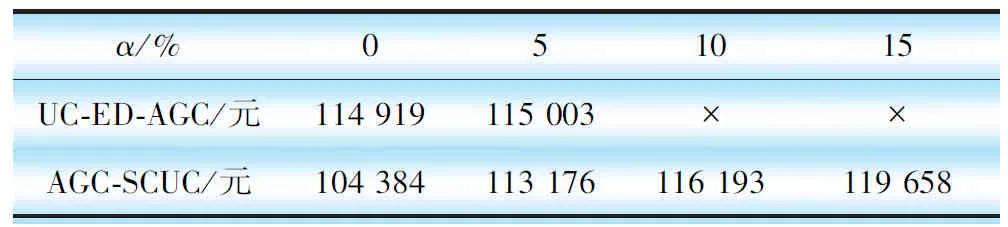
表3 考虑AGC容量约束的系统成本

表4—表6的结果是在在α取0%时得到的，表4是UC-ED-AGC模型的机组启停结果，其中1代表启动，0代表停止；阴影部分为与AGC-SCUC模型结果的不同部分。可以看出，2种模型的开停机结果不一样导致最终系统成本不一样。表5是UC-ED-AGC模型选定的AGC调节机组，其中阴影部分为与AGC-SCUC模型结果的不同部分。表6具体对比了2种模型各部分费用的大小，可以看出UC-ED-AGC模型虽然发电成本较低但是AGC费用很高，这是因为UC-ED-AGC模型在机组启停机固定的情况下，为了满足系统AGC需求，只能采用AGC费用较高的机组作为AGC调节机组，而使AGC调节费用很高。AGC-SCUC模型从整体上进行优化，虽然其结果发电成本较高但通过选择合适AGC机组，使系统的总成本降低。

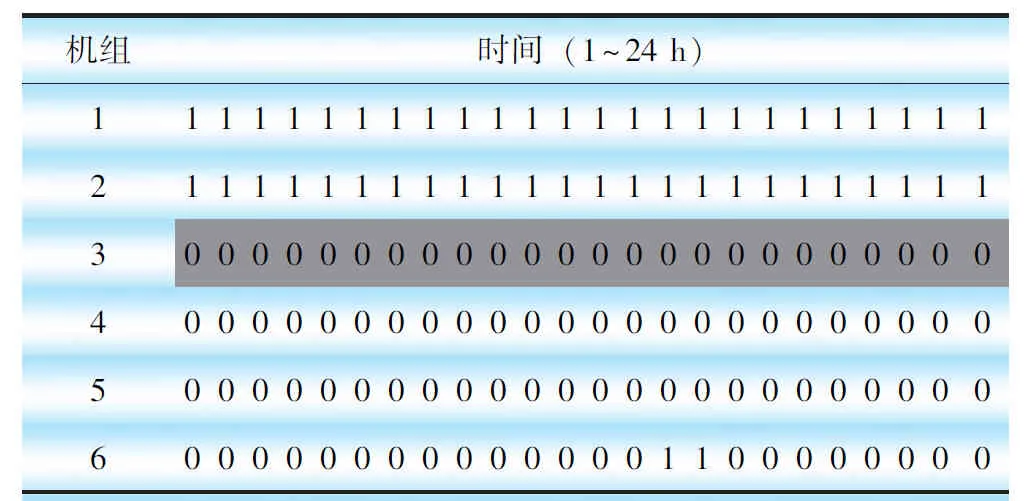
表4 UC-ED-AGC模型优化的机组启停结果

表5 UC-ED-AGC模型选定的AGC调节机组

表6 系统成本分析 单位：元

3.2 AGC爬坡能力对于系统的影响

传统的经济调度一般每5～15 min进行一次，但是风电在5～15 min之内的波动性仍然会很大，因此就需要AGC在此时间段内进行多次辅助调节。风电功率的波动速度、范围大，其对于AGC调节的能力要求更高，体现为系统需要的AGC爬坡能力增强。风电功率在2次相邻的AGC调节过程中的波动大小与风速变化大小和风电容量有关，AGC需要有足够的爬坡能力跟踪风电出力波动，维持系统功率平衡。本文定义系统AGC爬坡能力需求为式(27)，即每分钟的AGC爬坡能力能够满足风电出力的爬坡需求，其中β为一个反映风速变化的系数，将β取不同的值代表每分钟风速不同的变化，对比2种模型的结果，见表7。

SVU=βPwind

SVD=βPwind

(27)

表7 考虑AGC爬坡约束的系统成本

从表7中可以看出，随着风电波动爬坡速率的增加，系统需要的AGC爬坡能力增强，由于UC-ED-AGC调度模型不在机组组合阶段考虑相关约束，导致安排的在线机组不能提供足够的AGC爬坡能力，从而造成系统AGC爬坡能力不足。从表7中还可以看出，即使UC-ED-AGC模型能够满足系统AGC爬坡能力需求，其费用也要明显高于AGC-SCUC模型。

3.3 同时考虑AGC容量和爬坡的影响

表8对比2种调度模型在同时考虑AGC容量和爬坡约束时的系统费用。对比表3、表7和表8可以发现，当只考虑AGC容量约束时，α取0时UC-ED-AGC模型能够满足系统AGC容量约束；当只考虑AGC爬坡约束时，β取0.05，UC-ED-AGC模型也能够满足系统AGC容量约束；但是当同时考虑AGC容量和爬坡时，UC-ED-AGC模型却不能在α取0，β取5%时满足AGC容量和爬坡约束，说明机组的AGC容量和爬坡是互相影响的。具体解释如下，如果有2台机组在线，机组A的AGC容量较大但是AGC爬坡能力较小，而机组B的AGC容量较小但是AGC爬坡能力较强，如果只考虑AGC容量约束，那么机组A参加AGC调节能够提供足够的AGC容量，这时机组B不参加AGC调节，其出力区间较大，能够平衡系统功率；当同时考虑AGC容量和爬坡能力约束时，由于机组A的爬坡能力不强，无法满足系统需求，这就需要机组B也参加系统AGC调解，这样机组B的出力区间会相应减小，此时2台机组的出力区间之和就会减小，造成无法平衡系统功率，从而使系统无法求出可行解，因此可以看出AGC容量和爬坡约束之间是相互影响的。

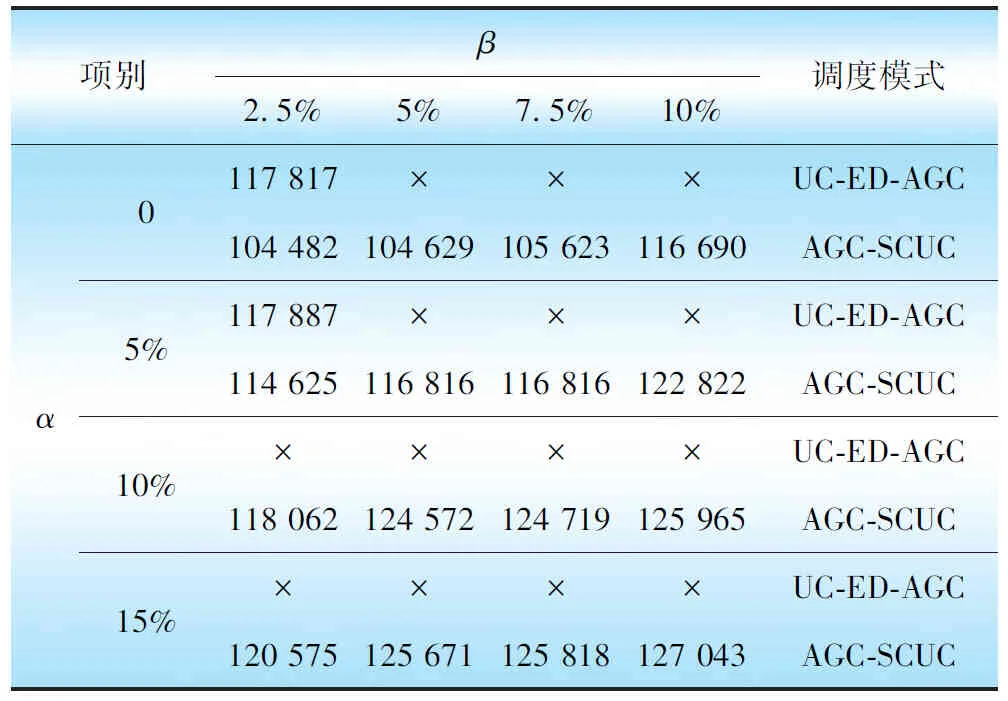
表8 系统费用 单位：元

AGC-SCUC模型在机组组合阶段就考虑了AGC相关约束，综合考虑了AGC容量和爬坡互相影响，因此能够保证系统预留足够的AGC容量和爬坡能力，并提高系统整体的经济性。

4 结语

本文提出了考虑AGC调节大容量风电的机组组合模型，该模型将机组组合、经济调度和自动发电控制这3种调度调节方法紧密联系到一起，在机组组合阶段就将AGC约束考虑进来，保证了机组组合方案能预留出足够的AGC容量和爬坡能力，满足系统在接入大容量风电后的AGC需求。通过与传统的UC-ED-AGC调度模型的比较，说明了考虑AGC调节大容量风电快速波动性的机组组合模型在安全性和经济性两方面的优势。