某边坡爆破施工对既有隧洞影响数值分析

罗卫华，陈彩苑

（1.广东省建筑设计研究院有限公司，广东 广州 510010；2.华南农业大学水利与土木工程学院，广东 广州 510642）

0 引言

爆破施工是目前工程施工中常采用的施工方法，但爆破产生的冲击波和动荷载对附近构筑物和建筑物的安全影响较大，尤其是爆破点距离建(构)筑物较近，且建（构）筑物是砖混，并年代久远时[1～9]。所以，为了研究爆破施工过程中的对既有建（构）筑物的影响，深入研究爆破动荷载作用下建（构）筑物的动力响应问题是十分重要和必要的。例如广州某大型垃圾填埋场的工程，在设计时根据地质资料，库区开挖需采用爆破，而邻近有新建的过水隧道，必须分析爆破时对既有隧道的安全影响进行分析。本文以边坡爆破施工工程为背景，应用有限元软件分析了某边坡爆破施工对既有供水隧洞安全影响，主要分析了不同深度、不同位置处爆破荷载产生的动力响应大小，并评估其对供水隧洞安全的影响，根据影响成果给出具体的减振措施，可为类似工程提供借鉴。

1 工程概况

拟施工边坡场地位于东莞市樟木头镇樟洋社区“石山排”，土石方爆破工程施工作业区域西侧约75 m(平行距离)为供水隧洞，隧洞顶标高约30 m，爆破位置处整平标高约70 m，隧洞比爆破地平线低约40 m。现状航拍图，见图1。

图1 现场航拍图

爆破工程施工作业区域与周边环境相互位置关系，见图2。

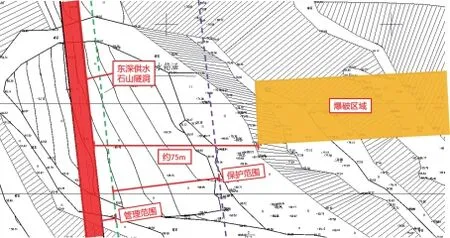
图2 爆破工程施工作业区域与隧洞平面位置关系

本次评估影响范围隧洞位于中风化花岗岩层，围岩等级III级或IV 级围。隧洞断面为城门洞形，过水断面尺寸为6.4 m×7.2 m（宽×高），2019 年年度检查未发现病害。III级围岩衬砌边墙及底板厚400 mm，顶拱厚400 mm，锚杆长2.5 m，间距1.2m×1.0 m；IV级围岩衬砌底板厚400 mm，边墙及顶拱厚500 mm，锚杆长3 m，间距1.2 m×1.0 m。

2 爆破施工振动效应的数值模拟分析

2.1 爆破施工方法

根据工程量、业主对工期的要求、工程现场的实际情况和工程特点，拟采用露天台阶深孔爆破为主，辅以浅孔台阶爆破的施工方案：

（1）台阶5 m以下区域采用浅孔台阶爆破法；

（2）台阶5 m以上采用深孔台阶爆破法；

（3）边坡采用预裂爆破法。

2.2 爆破安全评定依据

目前，评价爆破震动荷载作用下对邻近建筑物的影响，主要是以质点振动速度作为爆破地震效应的衡量指标。我国颁发的《爆破安全规程》（GB 6722—2014）[4]规定了质点振动速度作为安全判据，并根据萨道夫斯基经验公式给出了爆破地震波在不同性质的岩石中传播的相关系数的参考值。

爆破施工组织设计中爆破振动频率50 Hz 左右，综合设计参数与实际情况可能存在一些差异，根据《爆破安全规程》（GB 6722—2014）规定，水工水洞的安全振速为8～10 cm/s。鉴于供水隧洞的特殊性，本工程爆破隧洞振速按2.0 cm/s 进行控制。

2.3 爆破分析方法

此处采用M idas/G TS NX 有限元软件进行边坡爆破施工对既有供水隧道安全影响的仿真分析。利用有限元法求解爆破动力问题时，原理是把单个单元的质量平均分配在该单元结点上，形成整体质量矩阵，这样就形成了多质点振动体系，然后构建多质点振动体系的动力方程，最后依照多质点振动体系动力方程的求解方法，求出结构在爆破振动作用下的反应(位移、速度、绝对加速度。

首先需对模型进行特征值分析，求解整体模型各振型振动周期。在得到模型振型周期后，进行时程分析，求解结构在爆破振动作用下的反应。

在特征值分析中，利用弹性边界定义模型的边界条件，弹簧系数根据地基反力系数计算，其中：

竖直地基反力系数：

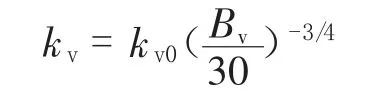
水平地基反力系数：

在时程分析过程中，采用了Lysm er（1969）提出的黏性边界条件，且需计算x，y，z 方向上的阻尼比，具体计算公式如下[2]：

P 波：

S 波：

式中：λ 为体积弹性系数，kN/m2；为弹性系数，kN/m2；G 为剪切弹性系数，kN/m2；A 为截面积，m2；v 为土体泊松比；γ 和ρ 取值按照供水隧道处的围岩级别取。

对于一般的爆破弹性分析爆破压力都是作用在孔壁的垂直方向上，此时的荷载用美国N ational H ighw ay Institute 里提及的公式。每1 kg 的爆破荷载如下。

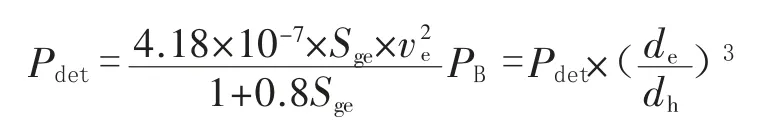
式中：Pdet为爆破压力，kPa；PB为孔壁面上的压力，kPa；de为火药直径，m m；Ve为爆破速度，m/s；Sge为比重；dh为孔眼直径，m m。

上式决定了爆破时发生的空气动压力的大小，作用在孔壁上的动压力随时间发生变化，经过对比分析，取常用的Statfield 提出的有关时程的动压力[2]：

这里，B 是荷载常量，每1 kg 装药量的动压力，即将装药量设为1.0 kg 后按照一种工况来计算爆破荷载。

设计每排爆破孔5～10 个，为了保证最靠近隧洞区域爆破面积最大，取每排炮孔10 个，即单段最大爆破范围4 排。爆破炮孔布置见图3。

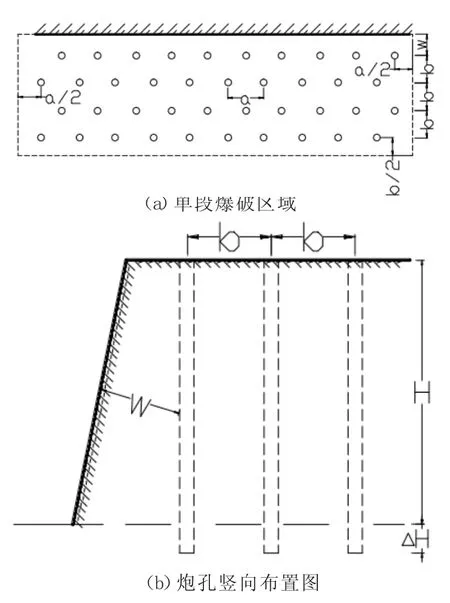
图3 炮孔布置图

根据《爆破设计》，炮眼距离：a=1.2 m；排距：b=1.0 m。可以取单段最大爆破范围为12.6 m×4 m。

2.4 计算模型及参数选取

土石方爆破区域距离隧洞最近距离约75 m，单段最大爆破范围为12.6 m×4 m。由此建立三维分析模型见图4。

图4 整体计算模型图

其中，图4 为整体计算模型，模型尺寸为166 m×100 m×90 m（长×宽×高），图5 为爆破区域与隧洞相互位置关系。

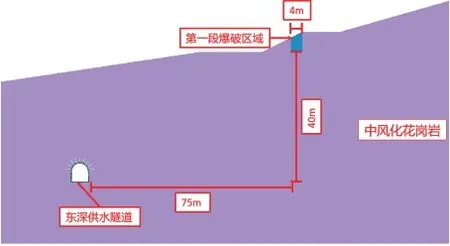
图5 爆破区域与供水隧洞相互位置关系图

根据《爆破设计》，4 m台阶爆破炮孔直径42 mm，炸药直径32 mm。由罗阳等人《相邻隧道围岩爆破振动影响规律研究》文献，乳化炸药爆压为0.32 G Pa，炸药密度为1.3 g/cm3，爆速为0.55 cm/μs。

依据前面计算爆破分析方法公式可得，Pdet=805.78 MPa，Pb=356.38 MPa，则每1 kg 乳化炸药爆破压力时程曲线见图6。

图6 爆破荷载时间历程曲线（炸药量为1 kg）

本次分析根据圣维南原理，主要分析爆破荷载对供水隧道的影响，距离离爆点有一定距离，将爆破孔聚集到一处后假定此压力同时作用在爆破的假想面上进行计算。

建模时候岩土层及结构材料参数取值见表1。

表1 岩土计算参数表

其中，混凝土用于模拟输水隧洞结构及挡土墙和桩基础结构，金属用于模拟输水隧洞锚杆结构。

3 计算结果

假定68kg 乳化炸药爆破所产生的荷载作用断面上，特征值分析中得到整体计算模型第一、二振型周期为24.57 s、23.127 s。时程分析时长设定为1 s，时间间隔设定为0.001 s，结果输出间隔10 步。

在最靠近爆破区域位置的隧洞顶部、肩部、底部共设立5 个观测点，观测点设置位置见图7。

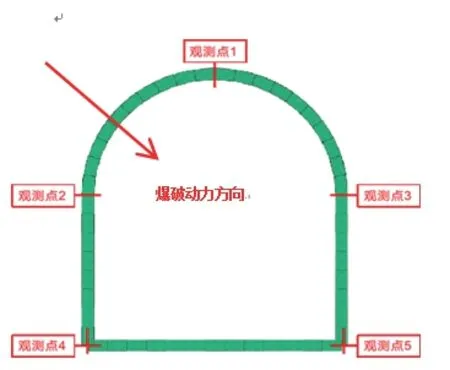
图7 观测点位置

各测点计算结果绘制成曲线见图8 和图9。

图8 测点速度-爆破时间曲线

图9 测点位移-爆破时间曲线

根据速度计算结果：各测点速度随着时间呈现出先增大后减小，最后趋于零的趋势，测点1 最大速度0.24 cm/s，测点2 最大速度0.22 cm/s，测点3 最大速度0.23 cm/s，测点4 最大速度0.21 cm/s，测点5最大速度0.21 cm/s，各测点速度均小于规范允许值2 cm/s。

根据位移计算结果：各测点速度随着时间呈现出先增大后减小的趋势。测点1 最大位移0.600 mm，测点2 最大位移0.546 mm，测点3 最大位移0.576 mm，测点4 最大位移0.499 mm，测点5 最大位移0.526 mm，各测点位移均较小，爆破对隧洞变形影响较小。

各时间段爆破振速云图见图10 和图11。

图10 爆破产生0.01 s 时刻地层振速反应图

图11 爆破产生0.10 s 时刻地层振速反应图

隧洞不同时间段振速云图见图12 和图13。

图12 爆破产生0.01 s 时刻隧洞振速反应图

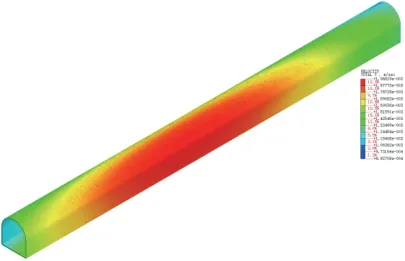
图13 爆破产生0.10 s 时刻隧洞振速反应图

隧洞不同时间段位移云图见图14 和图15。

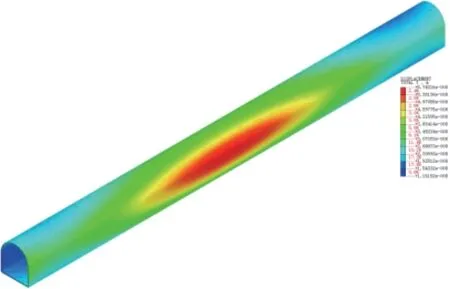
图14 爆破产生0.01 s 时刻隧洞位移反应图

图15 爆破产生0.10 s 时刻隧洞位移反应图

4 对隧洞影响的安全评估

根据数值模拟计算结果：各测点速度在0.21～0.24 cm/s 范围内，小于规范允许值2 cm/s。各测点位移0.499～0.600 mm 范围内，各测点位移均较小，爆破对石山隧洞变形影响较小。

综上所述，道路土石方爆破对东深供水工程石山隧洞有一定的影响，但影响在石山隧洞安全状态允许范围内，不会危及石山隧洞的安全和正常使用。计算得到的最不利工况下爆破荷载引起的隧道安全影响振速可知，爆破施工引起最大振速均小于安全振速控制标准（2.0 cm/s），说明爆破施工产生的振动对隧洞影响在相关规范允许范围之内。

5 优化爆破方案、采取减振措施

通过数值模拟分析，虽爆破施工期间对供水隧道的安全影响在可控范围内，但复杂岩土工程问题受计算参数、模型边界条件、爆破参数与实际爆破存在一定的差异，考虑供水隧道的重要性，为降低爆破施工对隧洞的影响，建议采取如下减少影响的措施：

（1）建议大范围施工前开展试爆破，并进行相应的监测，根据实测数据进一步优化爆破参数，并验证数值模型计算结果的合理性；

（2）如果施工期间，在爆破振速较大区域，可通过设置2～3 排减震孔或减震沟来降低爆破振动产生的影响和破坏；

（3）本次爆破的周围环境复杂，为了既能确保周边建筑物和构筑物的安全，建议对隧洞的监测（包括沉降位移、振速），动态监测，及时反馈结果，利用目前隧洞已经布置的健康监测系统（地面沉降、隧洞沉降和位移），在爆破施工前确定现有初读数，并可以为施工参数的调整、修正提供重要依据。

6 结语

本文结合具体工程，用三维实体数值模型计算分析了某边坡爆破施工对既有隧洞的安全影响，分析结果不仅指导了现场施工，可为爆破振动动力问题数值分析提供了借鉴作用。