基于K-means聚类的计算机视觉下杨梅水果图像识别
卢 巍
(昆明文理学院信息工程学院,昆明 650222)
0 引言
随着人工智能在工业和农业中的逐步运用,传统的手工业行业都在探索机器视觉下的自动控制技术,计算机视觉下的水果采摘也在如火如荼的研究当中。目前大多数计算机视觉下的水果采摘研究,关注点都放在水果品种和大小分类的算法研究上,而对直接进行果树上水果和背景分离的计算机视觉算法研究不多。这主要是当前市场对分链需求的导向所致。但是,从长远人工智能发展角度来看,机械采摘技术也会不断发展和运用。云南有着大量的大树杨梅种植,传统人工采摘技术耗工耗时,机械臂采摘可以解决这一问题。要研究机械臂采摘,就要解决计算机视觉下的水果和背景分离,使机械臂能准确定位水果,完成采摘。
1 K-means聚类基本原理
K-means 聚类是这样一种聚类算法,它用质心定义数据原型。算法开始时,将数据根据其到初始质心的距离不同随机指派到一个最近邻的质心形成簇。为了将数据指派到最近邻的质心,就需要一个邻近性度量来量化所谓数据的“最近”概念。在聚类算法中,通常使用欧几里德距离并同时对数据文档使用余弦相似性进行度量。可是,由于K-means聚类所使用的邻近性度量非常简单,因为算法要不断地重复计算每个数据点与质心之间的邻近度。考虑邻近性度量为欧几里德距离的数据。所以使用误差的平方和(sum of the squared error,)作为度量聚类质量的目标函数。也称为散布。换言之,计算每个数据点到近邻质心的欧几里德距离,也就是每个数据点的误差,然后计算误差的平方和。给定由两次运行后产生的两个不同的,我们更喜欢误差的平方和最小的那个,因为它说明聚类的质心可以更好地代表族的中心。的定义如式(1)所示:
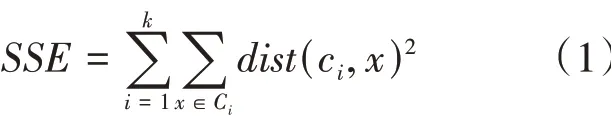
其中,是欧几里德空间中两个对象之间的标准欧几里德距离。对于给定一个,可以把聚类问题看为优化问题。更确切的说是可以看为一个全局最优问题,解决这个问题的一种方法是穷举法,即找到将所有数据点划分成簇的所有可能方法,然后选择最好的满足目标的一个。这种方法可以保证实现误差最小化算法,可是,在实际运用中,这种方法没有计算可行性,因此,需要寻找一个更加实际的方法,在数据挖掘领域一种常用的解决这个问题的方法是梯度下降法。这个方法虽然无法保证实现最优解,可是它却是实际可行的。对于这种方法,只需要选择一个初始解,然后重复计算最好的优化目标函数的解的改变和更新解这两个步骤。将其运用到要解决的问题中,现假定数据是一维的,即满足式(2):
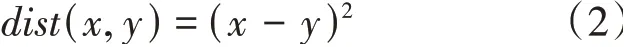
这个假设没有改变任何东西,但是可以大大地简化所需要的论证过程。现在的目标是最小化,因为最小化就可以得到K-means的最优化质心。对于式(1),当数据是一维数组的时候,可以简化为式(3):
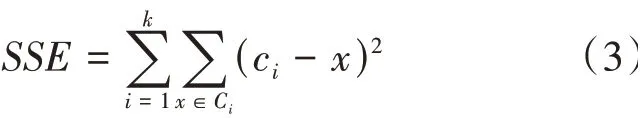
其中C是第个簇,是C中的点,c是第个簇的均值。
对第个质心c求解,最小化式(3),也就是对求导,求导过程如下所示,得到式(4):
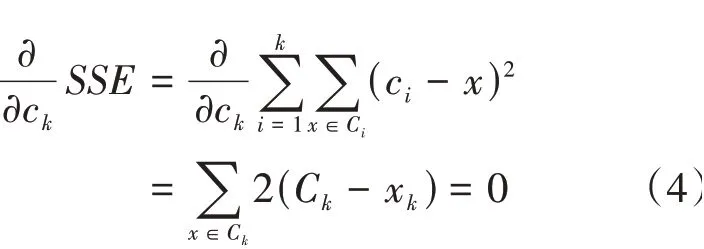
将式(4)进行进一步化简,可以推导得到式(5):

并最终推导得到式(6):
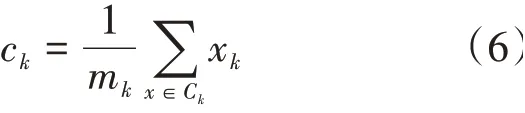
从式(6)可以看出一个重要的结论,簇最小化的最佳质心是簇中各点的均值。至此,证明了质心的最优取得是各点的均值。可是,同时也带来另外一个问题,这样的质心是否可以运用于各种不同的目标函数。这个问题在数学上可以表示为将数据划分为个簇,使得数据点到其簇中心的曼哈顿距离()之和最小。即把目标转化为寻求最小化,式(7)给出了的绝对误差和。
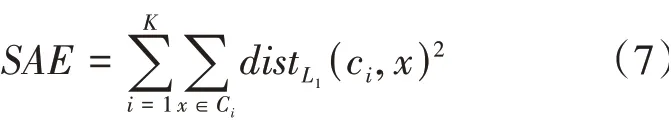
其中dist是的距离。为了简单起见,再次使用一维数据,即dist= ∣c-∣。
可以对第个质心c求解,最小化式(7),即对求导,令导数等于0,并求解c,得到式(8)。

对c求解,可以发现求解结果就是各点的中位数。同时,这也为计算带来方便,因为一组点的中位数的计算是简单明了的,而且受到离群点影响较小。以上解释了算法中用均值作为质心,同时,证明了这样的质心具有普适性。根据式(6),定义第个簇的质心(均值)为式(9):

K-means 算法接下来的步骤是最小化,这个步骤是通过将数据中每个点指派到最近邻的质心形成簇,判断是否达到局部最优,若没有,就更新质心,重新指派,直至达到局部最优。
总体来说,K-means 是以局部最优为原则,通过不断更新质心的迭代手段来实现对数据的聚类。其适应性较强,对数据所服从的分布没有任何依赖,为聚类一些服从复杂分布的数据开辟了一个新的空间。
模仿机械臂安装后计算机视觉成像距离进行图片拍摄,将拍摄好的大树杨梅图片先进行灰度化处理,处理后的数据进行拟合优度检测,运用柯尔莫哥洛夫-斯米诺夫检验(KS 检测),来判断图像数据的统计分布特性,进一步运用拟合优度检验法对其进行参数估计,建立基础分布模型,后尝试数据聚类。
2 算法设计
根据K-means 聚类原理,将其运用到前期处理好的图像数据中,根据实际图片情况,初始选取质心时,将成熟杨梅颜色数据均值,未成熟果实和树叶颜色数据和其它杂项数据均值选取为两个质心,进行算法迭代,算法流程如图1所示。

图1 K-means聚类算法流程图
根据图1 所示算法编写算法程序,运用Kmeans聚类算法分析所采集的实验图片数据,期望能证明其分类的有效性并找出此方法在数据运用中存在的不足。笔者在实验基地运用高清照相机采集400张成熟期大树杨梅的图像进行实验,为了实验方便,采用图形图像处理软件对图片进行归一化处理,将图片像素统一成800×600,并对图像做包括尺寸裁剪、滤波、图像增强、特征抽取和分割等预处理后进行聚类实验。
3 实验和聚类结果
实验中使用的数据信息如表1所示。

表1 测试样本参数对照
表1中3个测试样本均选取图片中包含20个成熟杨梅果实图片样本。3个测试样本都是同一角度下拍摄样本,但拍摄光线不同,测试样本一是在正常自然光线下拍摄,测试样本二为正常光照不充分时拍摄样本,模拟实际采摘中晨昏或者由于栽种密集而导致光线不足情况,测试样本三为夜间人为打光光线下拍摄样本。
实验:验证K-means 聚类效果为检验Kmeans 聚类算法数据的分类效果,运用K-means聚类算法对测试样本一和测试样本二进行聚类,其聚类结果如表2所示,表中显示分类正误个数和分类正确率。

表2 K-means聚类混合K分布数据效果
从表2可以看出,运用K-means聚类算法可以较好地聚类大树杨梅图片数据,测试样本迭代5 次达到收敛。在对测试样本一中400 个样本进行聚类时,正确率93.26%,说明在光线充足的情况下,通过聚类可以很好地识别成熟杨梅果实和其他颜色背景。但是在测试样本二中400个样本进行聚类可以看出,自然光照对算法聚类的准确性有一定影响。测试样本三的聚类效果不甚理想。分析原因,光照不充足,导致照片成像色彩变化,加之前期图像处理过程中引入的误差叠加,导致边界模糊所致,特别是当人为补光时,照片色彩和自然光线下照片色彩改变较大,使得边界模糊现象更加突出。
4 结语
以具有丰富信息的彩色图像为处理对象,本文给出了运用K-means 聚类算法对云南当地农作物大树杨梅进行聚类的一种算法,算法初始选取两个质心进行迭代,经过5次迭代,可以实现将大树杨梅成熟果实和其它背景识别的目标。同时,由于K-means 聚类对异常数据的敏感性,当图片数据边界模糊时,对质心的选取提出苛刻要求。综上所述,算法可以快速、准确地对杨梅水果图像进行识别,具有较好的鲁棒性和泛化能力,可为水果采摘机器人视觉识别系统提供技术和理论支持。

