波浪参数对起重船——吊物系统耦合运动响应的影响

孙雷 林美鸿 中交四航工程研究院有限公司

1.引言

正确认识影响船舶作业安全的主要因素，是保证船舶作业安全的重要前提。由于起重船装载的特殊性要求，在极短的时间内起吊数千吨重物，排水量急剧增加；由于吊物的重心要算在吊钩以上的上滑轮心轴上，该点距水面数十米、甚至上百米，使全船的重心瞬间提高，对船舶稳性极其不利；吊物的重量与吊幅的乘积产生巨大的倾覆力矩，对起重船的浮态产生很大影响，其静横倾角可能达到7°～8°，甚至更大。因此，施工海域的波浪参数对起重船动力响应进行分析和运动响应分析，对保证起重船海上作业安全具有重要意义。

随着船舶在波浪中运动计算方法的完善及模型试验技术的发展，船舶在波浪中的动稳性也逐渐受到学界和工程界的关注，对波浪作用下起重船-吊装系统的动力响应开展了大量的研究。Schellin等建立了八自由度模型起重船动力学模型，研究波浪作用下船体的动力学问题。Chin等用多尺度方法分析吊索吊重的动力系统，结果表明两倍于固有频率的激励会导致突发的跳动作为吊索回卷的反应。王学亮应用切片理论完成了对起重船的水动力系数分析，分别计算了起重船在规则波和随机波上航行和作业的船体运动响应，并考虑了起重船作业时的定位锚钢缆系统和起吊重物对船体运动响应的影响。任会礼等基于二维平面钟摆模型，对起重船吊臂柔性对系统动力学特性的影响进行了分析。夏益美等基于稳性计算原理，分析了仿真系统并建立了浮态计算数学模型；基于冲击外力矩下的船舶横摇数学模型，对起重船作业过程中的浮态、稳性和重物跌落后的船舶横摇角进行了计算。汪娟娟利用MOSES软件对船与吊重的六个自由度的运动进行研究，分析了系泊缆预张力、吊绳长度、吊重、吊距等要素对吊物及船体运动的影响。赵景浩采用水下运载体六自由度方程建立吊装物模型，析了深水吊放系统中安装母船、缆绳及吊物的动力响应，获得了缆绳切向无阻尼动态张力的近似解析解和切向无阻尼然频率的表达式。董达善等基于多体动力学建立了刚柔耦合浮吊作业的虚拟样机模型，获得得出浮吊在海上补给作业的相关动力学特性。

目前国内外对于起重船的作业安全的研究主要聚焦于作业耐波性能研究、水动力耦合定位性能分析、稳性分析等。本研究拟对起重船—吊物系统进行水动力建模，分析起重船——吊物耦合系统在不规则波中的运动响应，并分析波高、波周期和遭遇角等波浪参数对起重船-吊物系统的耦合运动响应的影响。

2.势流理论

在不可压缩的理想流体中，无旋场中的速度势应满足拉普拉斯方程：

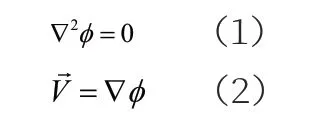
势函数分为入射势、衍射势和散射势，具体的效应产生的力可由对应波势进行计算。作用在浮体上的波浪力认为是波浪激发的力，通常可以分为两部分：波浪主干扰力和绕射力；浮体的运动使得流体作用在浮体上产生辐射波应力，这些力用附加质量和波浪阻尼系数来表示。

考虑衍射辐射的一阶波浪力的势函数可写为：

式中，φ为入射波势；φ为衍射波势；φ为j自由度运动产生的波势；x为j自由度运动；ω为入射波频率。

无扰动三维入射波势可以表示为：

式中，d为水深；k为波数；θ为波浪入射角（与x轴夹角）。

当势函数求解出来后，一阶水动压力分布可根据线性伯努利方程求解：

根据压力分布，各种流体力可以通过对压力在湿表面的积分得到一阶波浪力：

式中，F为j自由度运动激发的力；n为表面法向量；S为浮体湿表面。

波浪对浮体产生的力（入射力）可表示为下面两部分：

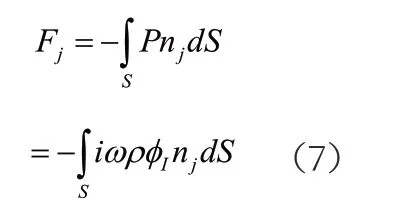
由运动产生的辐射力可表示为：

获得浮体在频域下的一阶运动方程，即浮体在波浪下的的运动响应：

其中，M(s)为结构质量矩阵；M(a)为附加质量矩阵；C为系统线性阻尼矩阵；K(s)为系统总刚度矩阵；F为单位波高时系统所受的波浪力；X为幅值响应算子。

3.耦合系统的水动力建模

ANSYS AQWA基于三维势流理论而开发，由于仅在结构与水体的接触面进行离散，计算总未知数相对较少，求解效率很高，并考虑了邻近浮体的流体动力学相互作用。可考虑包括风、浪、流、缆索拖曳等各种荷载的综合作用，可以对各种施工工况进行组合，更适用于工程计算。

3.1 模型参数

起重船的主要参数见表1；系统系泊选用四点八字系泊，系泊缆与船长方向呈30°。

表1 起重船的主要参数表

3.2 水动力建模

使用AQWA软件，建立起重船主船体的三维的模型，依次建立其上层建筑和臂架等结构。以水线面为界，将其分成上下两个部分，对其进行网格划分，建立起重船水动力模型。以一长方体模拟实际吊物，赋予其重量和转动惯量等物理属性，通过四根吊缆将其与臂架相连，使用线性缆索单元模拟吊缆，起重船-吊物耦合系统水动力模型如图1和图2所示。

图1 起重船-吊物耦合系统水动力模型

图2 起重船的系泊建模

4.数值分析及验证

4.1 数值求解

在AQWA中设置外部环境的水深20m、海水密度1025kg/m、重力加速度为9.806m/s，以及水动力模型的质心、质点、惯性半径，由AQWA自动控制计算水动力模型的重量和惯性质量。取波浪周期分别为5s～20s（共计16个周期）；波浪遭遇角分别为0°、30°、45°和90°。对该耦合系统的水动力模型进行LINE模块的分析；用JONSWAP谱密度模拟不规则波，使用DRIFT模块对起重船和吊物（箱梁）的耦合模型进行时域下的水动力分析，设置计算时间为3200s（迭代步长为0.04s，总计算步数为80000步）。计算起重船和吊物耦合系统的六自由度运动。

4.2 水动力计算和验证

以波高为1.0m、波浪周期6s的不规则波，吊物重量1500t，波浪遭遇角为45°，系泊缆的预张力为170kN的工况作为标准工况。以目标吊物作为荷载条件，施工海域环境为外部边界条件，研究起重船-吊物系统在海况作用下的姿态及吊物摆动。选取起重船和吊物定常运动的六自由度运动姿态作为施工和对比的时间窗口（基本是1500s的运动），获得起重船和吊物的运动。起重船和吊物的六自由度运动能在400s～500s内稳定到定常运动。水动力计算和现场测试对比结果表明，起重船的横摇和纵摇的幅值与姿态仪实测的数据相吻合，横摇的幅值在0.1°范围内，纵摇的幅值基本是0.2°-0.3°之间。

5.波浪参数对耦合系统运动的影响

5.1 波高的影响

分别计算起重船-吊物系统在波高1.0m、1.5m、2.0m和2.5m工况下起重船和吊物系统的的六自由度运动。不同波高工况下的起重船和吊物的垂荡、横摇和纵摇的运动时历曲线分别见图3和图4。图3起重船的运动表明，在周期为6s以内的常见波中，随着波高的增加，起重船运动的幅值均变大，运动幅值与波高呈线性关系；图4吊物的运动表明，随着波高的增加，运动幅值与波高也呈线性关系。此外，波高的变化并不影响起重船和吊物的运动周期。

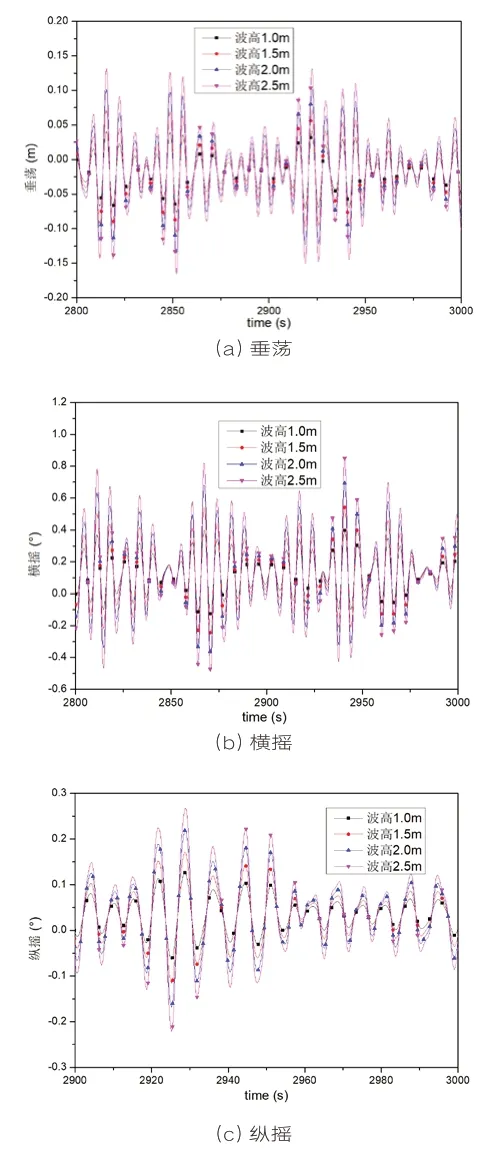
图3 不同波高下起重船运动时历曲线

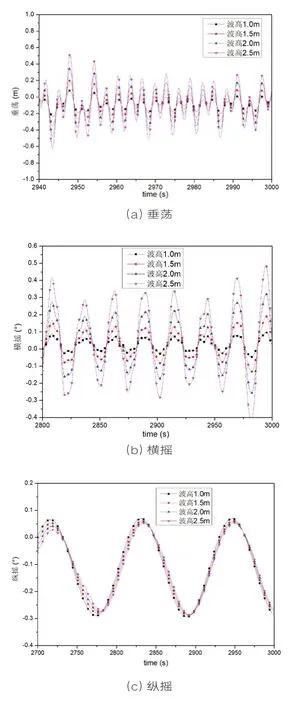
图4 不同波高下吊物的运动时历曲线

5.2 波浪周期的影响

分别计算起重船——吊物系统在周期为6s、10s、12s和16s的JONSWAP不规则波谱中的起重船和吊物系统的运动。不同波浪周期下的起重船和吊物垂荡、横摇和纵摇时历曲线分别见图5和图6。图5起重船的六自由度运动表明，在周期为6s～16s的范围内，随着波浪周期的增大，起重船的运动幅值均有不同程度的增大；但是其横摇和纵摇的运动的幅值并不是随着波浪周期的增大呈增函数的形式，而是在周期10s左右达到峰值，因为起重船-吊物系统的横摇和纵摇固有周期分别为8.98s和9.67s，起重船在周期10s 左右的波浪中会发生谐摇，吊装作业时应尽量避开周期为9s-10s左右波浪。图6 吊物的运动表明，除吊物的纵摇运动以外，吊物的运动幅值均有不同程度的增大。

图5 不同波周期下起重船运动时历曲线

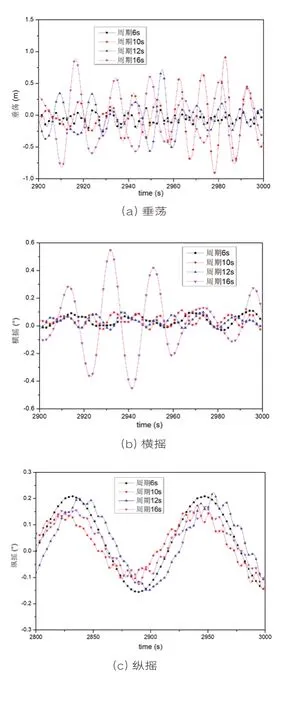
图6 不同波周期下吊物的运动时历曲线

5.3 波浪遭遇角的影响

分别计算起重船与波浪的遭遇角为0°、30°、45°和90°工况下起重船和吊物系统的运动。不同波浪遭遇角工况下的起重船和吊物垂荡、横摇和纵摇运动时历曲线分别见图7 和图8。图7起重船的运动表明，起重船的运动随着遭遇角的增加而变得剧烈。图8吊物的运动表明，在0°～90°的范围内，吊物运动随着遭遇角的增加而变的更加剧烈；除纵摇外，90°遭遇角时，吊物的运动幅值是0°时候的10倍以上。综合起重船和吊物的运动响应受到波浪遭遇角的影响，建议吊装作业时，起重船与波浪的遭遇角选为0°或180°。

图7 不同遭遇角下起重船运动时历曲线

图8 不同遭遇角下吊物的运动时历曲线

6.结论

本文基于水动力学势流理论的计算方法，使用ANSYS AQWA软件对起重船——吊物系统进行了水动力建模，包括起重船、吊物、系泊系统和吊装系统，对起重船-吊物系统在不规则波中的耦合运动响应进行了分析。对比分析了波高、波周期和遭遇角等波浪参数对起重船-吊物系统的耦合运动响应的影响，为起重船吊装作业时海况窗口期的选取和运动姿态的控制提供支撑。获得主要结论如下：

（1）在周围为6s以内的常见波中，随着波高的增加，起重船的起重船和吊物的运动与波高呈线性关系，但对吊物的纵摇影响不太显著。

（2）在周期为6s～16s的范围内，随着波浪周期的增大，起重船和吊物的运动幅值均有不同程度的增大，但吊物的纵摇运动除外；起重船横摇和纵摇固有周期分别为8.98s和9.67，在周期10s的波浪中，起重船横摇和纵摇响应最为剧烈。

（3）在波浪遭遇角0°～90°的范围内，遭遇角对吊物的纵摇运动不大，起重船和吊物其他自由度的运动随着遭遇角的增加而变的更加剧烈。