基于统一强度理论的螺纹桩承载力计算方法

螺纹桩是一种由桩芯和连续螺牙组成的异形截面桩，因形似螺丝钉而得名.其前身包括螺旋钢桩(螺牙为分离式，一般为1～3片)、预制螺纹桩、Atlas 桩等，最初由吴敏等借鉴国外相关桩型设计而成，具有良好的承载性能.

近年来，螺纹桩凭借其承载力高、沉降较小、施工效率高、经济环保等优点在房建及交通工程基础设施建设领域中得以广泛使用.然而，目前关于螺纹桩承载机理的研究却主要集中在数值模拟、模型试验及现场试验等方面，倾向于从宏观角度分析螺纹桩承载机理.李成巍等通过模型试验和数值分析，研究了螺纹桩的竖向承载机理，发现影响螺纹桩竖向承载力的关键因素为土体抗剪强度指标、螺距及螺牙高度.王国才等通过Abaqus对螺纹桩竖向承载特性及影响因素进行研究，发现螺纹桩极限承载力随(为螺距，为外径)先增大后减小，并在处于0.5～2时达到最大值.孟振等通过室内模型试验对比分析发现在相同条件下，螺纹桩的极限承载力约是普通桩极限承载能力的1～4倍，而蒋鹏程发现螺纹桩极限承载力比普通桩单桩提高了67%.

在螺纹桩极限承载力计算方面，常规方法仍以混凝土圆桩承载力计算方法为基础进行适当修正，主要包括将螺纹桩极限侧摩阻力乘以一定放大系数、将桩土极限侧摩阻力替换为土体抗剪强度或者将螺纹桩简化为多支点的摩擦端承桩等.这类方法忽略了螺牙与桩间土的局部相互作用，承载机制不清的同时阻碍了计算精度的提高，易造成工程实践浪费或安全隐患.因此，若要实现螺纹桩承载力的准确计算，必然要明确螺牙与桩间土的相互作用规律，尝试基于解析手段揭示螺纹桩的承载机理.

综合当前国外螺纹桩破坏机制的研究成果可以发现，关于螺纹桩破坏机制的研究尚不多见，且主要集中于螺纹桩的前身螺旋钢桩.有关螺旋钢桩的研究最早开始于20世纪60年代，已提出了多种破坏模型：叶片支撑破坏模型、圆柱破坏模型、单层叶片对数滑裂面破坏模型等.然而，螺纹桩在构造特点上与螺旋钢桩具有较大差异，相关理论的普适性尚有待商榷.国内关于螺纹桩破坏机制的研究处于起步阶段，目前关于这方面的报道为数不多.董天文等认为桩受荷载后桩顶处螺牙下方地基出现压密区，继而压密区向外挤出产生滑裂面，最终形成梨形滑裂面破坏区，螺牙端阻力达到极限；继续加载则螺牙间土柱被剪切破坏，下级螺牙开始承载，直至整个桩体发生破坏.孟振提出极限荷载下螺纹桩的两种破坏模式，即“单独承载破坏”与“圆柱形剪切破坏”，并分别讨论了两种模式下的承载力计算方法及破坏模式的判别方法.

然而，上述理论计算方法采用的屈服准则一般为单切应力屈服准则——Mohr-Coulomb(M-C)屈服准则，忽略了中主应力对土体屈服与破坏的影响既有研究表明，往往对材料的强度起到提升作用，而M-C屈服准则推导的地基承载力显然不能反映地基实际情况，结果偏于保守，具有一定不足.

鉴于此，本文拟基于双剪统一强度理论，以太沙基极限平衡理论为基础提出螺纹桩的承载力计算公式，通过工程实例验证计算公式的准确性及适用性，进而讨论了统一强度理论参数(该参数反映了中间主切应力对材料屈服的影响)及螺纹桩关键参数对螺纹桩承载力的影响，以期进一步完善螺纹桩承载理论体系.

1 双剪统一强度理论的M-C表述

双剪统一强度理论数学表达式为

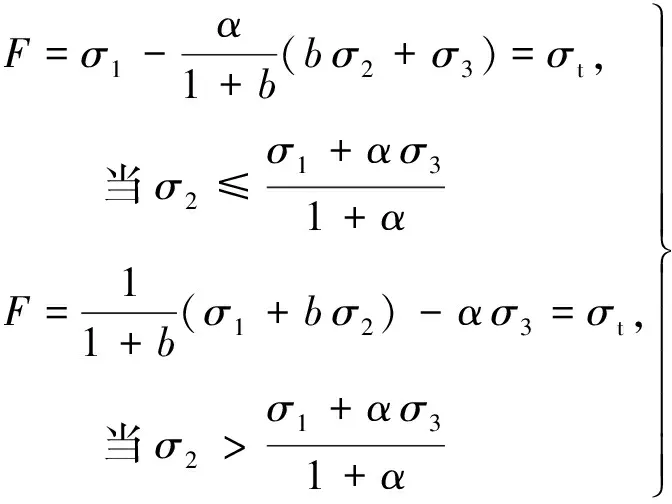
(1)

根据既有研究，当采用土体黏聚力与内摩擦角作为基本参数时，可转换为M-C屈服准则形式：

假定螺纹桩穿过层土体，第层土体厚度为，内摩擦角及黏聚力分别为t、t，重度为，则螺牙产生的竖向承载力之和为

=+tan

其中：、分别为屈服面上正应力与切应力；、分别为统一黏聚力与统一内摩擦角.

该准则具有与M-C屈服准则同样的表达形式，却可以合理考虑中主应力效应.极限平衡状态时计算表达式为

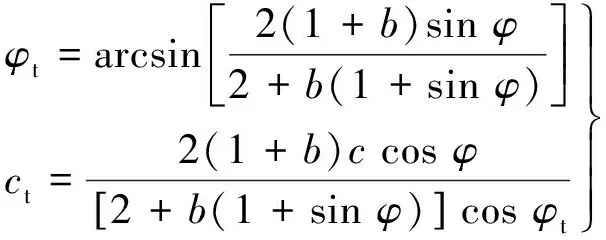
(2)

2 螺纹桩承载力推导

2.1 极限平衡理论及假定

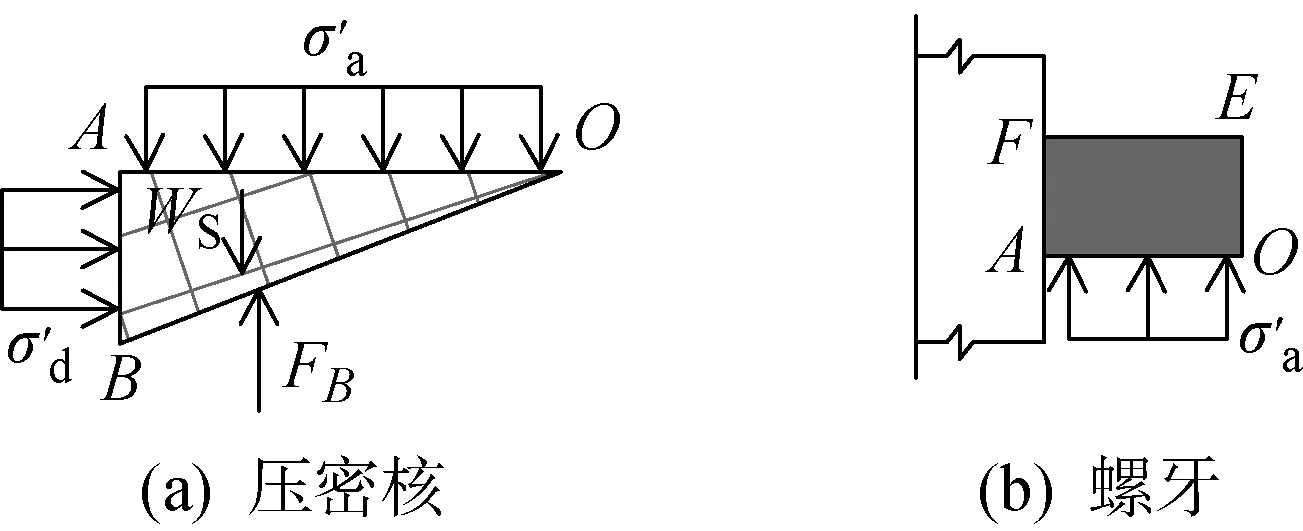
对于单独承载破坏模式的螺纹桩，根据太沙基地基极限承载力计算方法，螺牙下土体分为3个区域，如图1所示.图中：面为螺牙底部；面为螺牙顶部；π4-2为朗肯被动状态区面与水平面的夹角；为面上的均布压力3个区域包括弹性压密区、辐射向剪切区、朗肯被动状态区，曲线为对数螺旋曲线，形式为=etan ，其中为旋转半径，为初始半径，为旋转角.本文在推导螺牙极限承载力时，基于太沙基极限平衡原理的假定，同时结合工程实际对计算模型进行了一定的简化，作出如下假定：

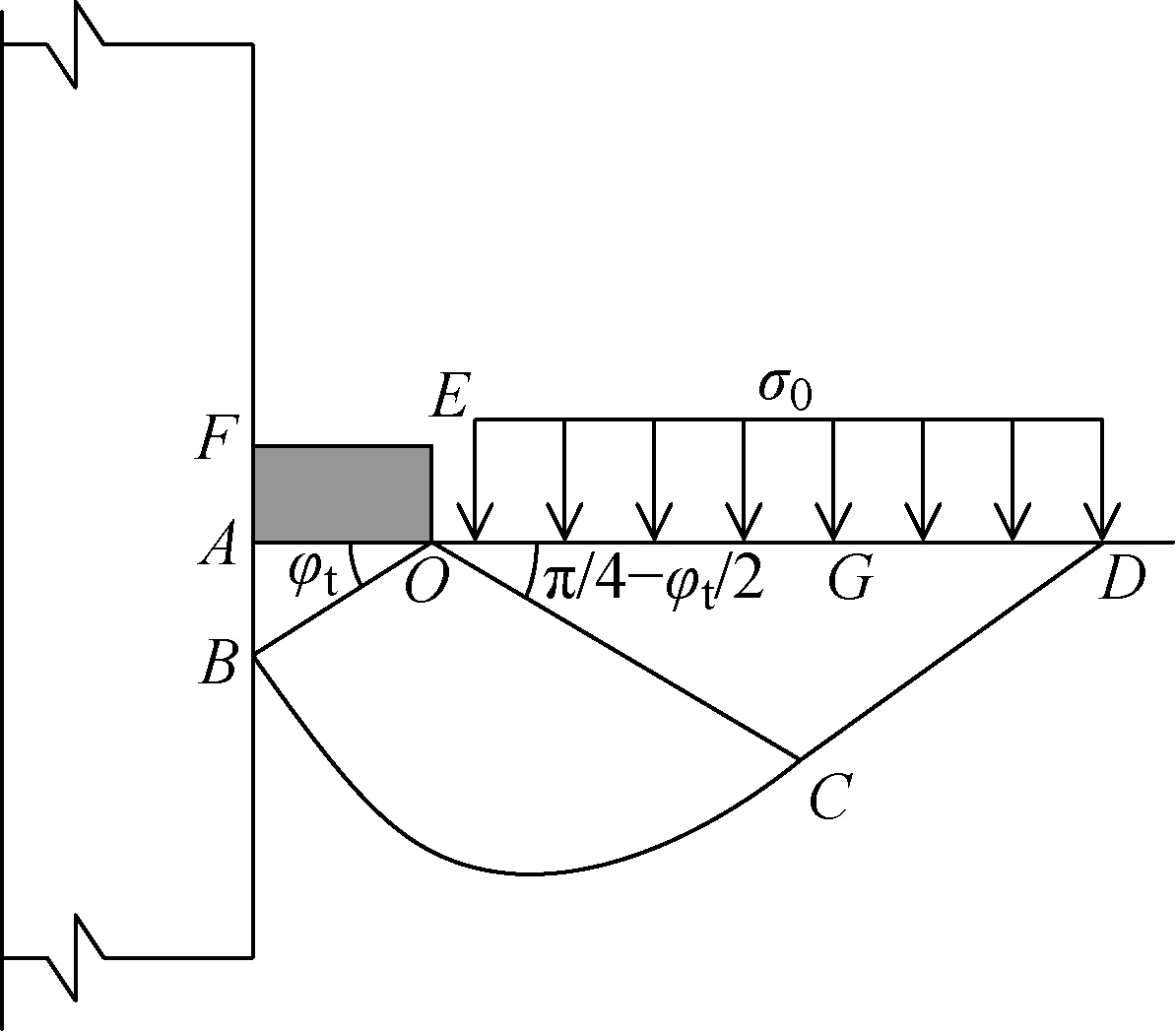
(1)考虑到实际工程中灌注桩与土体的摩擦及咬合作用，假定螺牙下底面完全粗糙，压密区与螺牙下底部夹角为，螺旋线中心为点，同时假定计算由滑动区自重引起的承载力时螺旋中心线也是点

马来西亚测绘局（JUPEM）为了推进马来西亚空间数据基础设施（MyGDI）建设，于2002年12月设立了马来西亚地理空间数据基础设施中心（MaCGDI），归马来西亚自然资源与环境部（NER）领导，取代了之前的土地信息系统国家基础设施秘书处（NaLIS）。MaCGDI负责协调各级政府部门的地理空间信息存取与分发工作，确保能不间断地存取和使用最新的、最精确的地理空间数据。

基础医学“整体功能”立体教学模式的实施是一项系统工程，它涉及到教学理念、教学管理、教学模式、教学内容以及教材等多方面的改革。以提高医学生岗位胜任力为目标的“三导向”培养模式下，专业素质培养过程中构建了具有我院特色的基础医学整体整合课程体系，在实践中我们将加强对教师和学生的全方位评价，随着经验的积累，我院的“整体功能”立体教学模式必将不断地发展与完善，并将为兄弟院校的教学模式改革提供有益的指导和借鉴。

在社会工作专业教育的“非传统”视角下，上述机构所需的人才培养完全是可以嵌套在已有的社会工作硕士项目的培养环节之中，而社会公益高端人才的培养也是属于社会工作专业教育与培养范畴内应该关照的重点。遗憾的是，我国第一个旨在培养具备社会责任感、创新意识、管理能力和实践能力，并致力投身于社会公益事业的高级管理人才或社会企业家的社会公益管理硕士项目(Master of Social Enterprise Management，简称MSEM)，却是由上述的传统意义上只关注于市场或企业领域经管人才培养的北京大学光华管理学院与中国银泰投资有限公司、北京银泰公益基金会发起和推行的。

(3)假定边上竖向力均匀分布且仅考虑土体自重，即=

上述3个假定中，实际上面上的侧摩阻力略大于tan，这里主要忽略了极限承载状态下桩土界面间残余黏结力，考虑到该值与侧摩阻力相比较小，故而未计入此外，面上竖向应力取时忽略了土体之间抗剪强度提供的竖向应力，小于实际值，然而该面上的竖向应力分布形式及数值的选取一直未得到精确解答本文参考太沙基推导地基极限承载力时所作假设，假定面上的竖向压力为均匀分布，其值取

2.2 螺牙极限承载力计算

根据太沙基研究成果，从实际工程要求的精度出发，计算基础极限承载力时可将其分为3种原因引起的极限承载力的总和：① 土体无质量，有黏聚力和内摩擦角，无超载，即=0，≠0，≠0，=0；② 土体无质量，无黏聚力，有内摩擦角，有超载，即=0，=0，≠0，≠0；③ 土体有质量，无黏聚力，有内摩擦角，无超载，即≠0，=0，≠0，≠0本文将前两种原因归为一类进行计算.

美方语料在构建IDC元素时，大量应用指示“特朗普”的名词词组及辅助词项“特朗普政府”“USTR”，突出特朗普及本届政府推行的政策与往届政府不同，宣称其更符合美国人民利益，试图增强特朗普的声望，赢得选民支持。因而，“美国人民”“我们”都成为IDC的重要元素，努力构建特朗普亲民的形象，通过人民的支持获得其政策的合法性。复数名词“农民们”“工人们”“消费者们”通过转喻机制指代美国人民，但将其具体化的话语优势在于引导民众相信总统在给予人民真切的人文关怀。

(3)螺牙竖向应力.

(1)面上的应力.

对于螺旋过渡区(区域)，滑动面上土体正应力与切应力之间关系为=tan+，其中正应力与其产生的摩阻力tan的合力与滑面法向夹角为，即指向螺旋线的中心，如图2所示图中：为螺旋曲线的最大旋转角；为螺旋曲线的旋转半径；、分别是面上的正应力、切应力；为面上的正应力；指数螺旋线的方程为

=etan

滑动面上取微段d对点求力矩，则d=dcos=d，其中为滑动面长度，为弯矩由点力矩之和为0可得(不计入滑动区重力)：

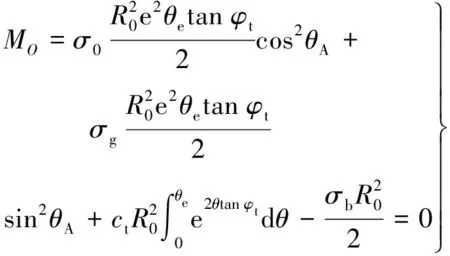
(3)

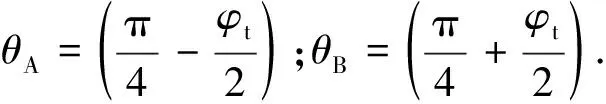
由式(3)解得：

=(cos+tansin)+

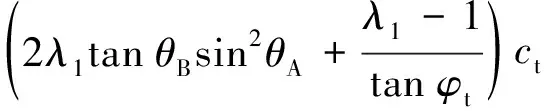
(4)

=tan+

(5)

(2)面上应力.

对于弹性压密区，假定螺牙达到极限承载力时，面上只有正应力，而无切应力，如图3(a)所示.图中：为螺牙底面与土体之间的法向应力；为表面与压密核之间的法向应力.则由方向力系平衡关系可得：

∑=

sin+cos-cos=0

(6)

式中：∑为方向的合力.

解得：

(2)假定承载极限时面正应力为=，其中为静止土压力系数，为土体重度，为埋深；切应力=tan，为桩土界面摩擦角，取065，面上土体与螺牙分离，二者相互作用为0

=+tan

(7)

..由埋深、黏聚力、摩擦角产生的承载力

对螺牙受力分析，假定螺纹桩在达到极限承载力时，面与土体脱空，二者之间无相互作用，此时螺牙上受到的竖向力除之外，还包括，如图3(b)所示.因此螺牙上平均竖向应力为

有涂层的原始样品表面和截面的扫描电镜图如图4所示.图4(a)显示，样品表面有起伏不平的扁平凸起，没有孔洞.图4(b)显示，涂层和碳钢基底之间结合紧密，看不到缝隙，涂层内部干燥后没有裂纹.将有涂层的样品在500 ℃加热8 h后，其表面和截面扫描电镜图如图5所示.图5(a)显示，样品表面基本上是平坦的，依然看不到孔洞.图5(b)显示，涂层和碳钢基底之间结合紧密，看不到缝隙.

式中：为螺牙厚度；为螺牙高度；为与黏聚力相关的承载力系数；为与埋深相关的承载力系数.

哄的一声，人群突然散开，把我挤在了前面，两副担架被人抬了出来。从身材的魁梧程度看，第一个抬出的应该是二狗子，只见那露出的胳膊，密密麻麻布满了针眼。

..螺距大于临界螺距 若上下螺牙塑性区不相互影响，二者之间的距离必然要大于某一数值，将其命名为临界螺距.根据Rao等的研究，若螺旋钢桩(螺纹桩前身)达到极限承载力时产生圆柱形剪切破坏，/的值需小于3，考虑到螺旋钢桩外径一般为其内径的数倍，因此/的值实际由叶片的螺距与悬臂端长度(对应于螺纹桩的螺牙高度)的比值来决定.因此，确定混凝土螺纹桩临界螺距时，需对上述方法进行一定的修正.结合《螺纹桩技术规程》，本文建议当与的比值/<6时，计算螺纹桩极限承载力采用圆柱形剪切破坏模型；当螺距/>6且>时，采用单独承载破坏模型，即此时>.

面上的侧向压力呈三角分布，切应力为0，则其合力作用于距离点3处，块体受力如图4所示而面上反力作用于距离点23处，并且与面法向夹角为，其方向为竖直向下.

对于区域，面上反力正指向点，对点取矩为0同时，取面积微元d，该微元土体到点的水平距离为，假定微元位于点左侧时为负，右侧为正，则=-cos(+)，微元重力对点力矩为

d=d=-ddcos(+)

式中：为面积微元到点的距离由点力矩为0可得：

乍见此人，老太医和乔十二郎都大吃一惊，此人竟是刑部赵大人。乔十二郎刚想喊一声“赵伯伯”，赵大人却不看他一眼，微笑着径直走向老太医。

(5)“有效氯含量”可用来衡量含氯消毒剂的消毒能力,其定义是:每克含氯消毒剂的氧化能力相当于多少克Cl2的氧化能力。NaClO2的有效氯含量为____。(计算结果保留两位小数)

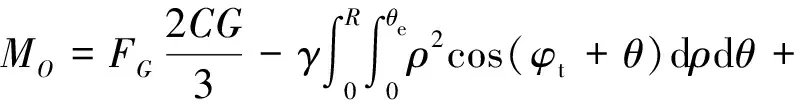
(9)

式中：为面上的合力；为土块的自重.

解得:

译文二：是不是他的太太有私房钱？瞎掰！弗林特小姐出身于白金汉郡的一个小地主家庭，兄弟姐妹连她共有十一个人。

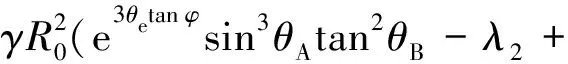
e3tan sincos)2cos

对于承台受力，内力控制截面为XY截面Z向压力，在左线隧道掘进后0#承台变化量为0.14%，1#承台变化量为1.1%；弯矩控制截面为YZ截面Y向弯矩，0#承台变化量为-2.4%，1#承台变化量为-7.6%，由此可见隧道掘进引起的承台内力变化较小。

(10)

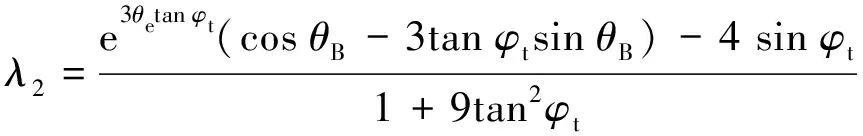
(2)块受力.

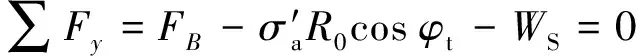
(11)

式中：为压密核自重.

解得：

(12)

即由土体自重引起的螺牙上平均竖向应力为

式中：为与土体重度相关的承载力系数.

综上，螺牙达到极限承载阶段时所受的竖向压力为

目前，GLP-1对β细胞的保护作用已经得到证实。其对β细胞的保护作用，主要是在促进β细胞增殖、诱导β细胞再生以及抑制β细胞消亡等方面发挥其作用。GLP-1对β细胞的保护作用机制尚未十分清楚，可能与以下几个方面的因素有关：①GLP-1受体激活后主要通过T细胞核因子或β连锁蛋白所依赖的Wnt信号系统，调节β细胞增殖和胰岛素生成的关键因子，从而刺激β细胞的增殖，促进β细胞的生存；②在体外β细胞系，GLP-1受体的激活能够保护β细胞细胞功能，免受各种损伤因素的影响。此外，有多种证据表明GLP-1可以诱导胰腺细胞、小肠表皮细胞以及胰腺中胰岛来源的前体细胞分化成为β细胞或具有分泌胰岛素功能的细胞[9]。

(14)

2.3 螺纹桩极限承载力计算

(1)块受力.

当>时，螺纹桩承载力由螺牙承载力、桩芯侧摩阻力、桩底承载力3部分组成.

(1)螺牙承载力.

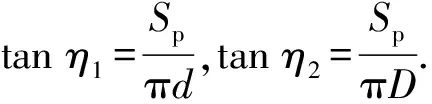
d高度内，螺牙竖向投影面积为

式中：为埋深.

式中：Bd —燃料消耗量（kg/h）；ey —空预器出口空气 （kJ/kmol）；e0—空预器入口空气（kJ/kmol）；—燃烧和脱硫当量理论空气量（m3/kg）；eCO2—炉膛出口二氧化碳 （kJ/kmol）；—环境温度下二氧化碳 （kJ/kmol）；—烟气中二氧化碳体积（m3/kg）—烟气中过量空气体积（m3/kg）；ekl —炉膛出口空气 （kJ/kmol）。

“在雪夜晒月亮，我们都快冻成四根凌冰挂树上了，你们两位就披一件葛布的袍子，不冷吗？乌有先生你还摇着你的纸扇子，会伤风的啊！”上官星雨说。

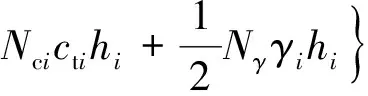
(15)

式中：、分别为土层编号；为第层土体厚度；为第层土体重度；q、c、γ为第层土体承载系数.

(2)桩芯侧摩阻力.

螺牙下土体受力状态复杂，压密核附近的竖向承载力主要由螺牙提供，本文在计算桩芯侧摩阻力时不计入压密区的摩阻力，上下螺牙间有效桩芯摩擦高度为

=--

(16)

式中：为螺牙下侧滑动边界与点的最大竖向距离.

螺旋线边界上任意一点与点的竖向距离为

=etan sin(+),+⊂(0，)

(17)

对求的导数，令其等于0，得：

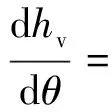
etan [cos(+)tansin(+)]=0

(18)

..由滑动区自重产生的极限承载力

因此：

(19)

螺纹桩桩芯有效摩擦区展开后如图7所示，图中(=0,1,…,)为第层土体底部埋深，为螺牙旋转周数取微元面积d，则d=ddtan，考虑到埋深远大于，忽略土体高度引起的侧摩阻力，故而微元面上的极限摩阻力为

式中：为桩芯侧摩阻力；为第层土体静止土压力系数；()为埋深处的土体自重应力.

桩芯极限侧摩阻力为

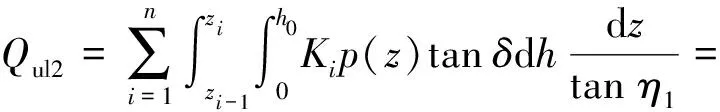
(20)

(3)桩端承载力.

计算桩端承载力时，桩端面积按桩芯底面积来计算，即=π/4，根据《建筑桩基技术规范》，极限端阻力标准值为

=

(21)

式中：为端阻力标准值.

综上，螺距大于临界螺距的螺纹桩极限承载力计算公式如下：

=++=

(22)

..螺距小于临界螺距 当≤时，上下螺牙之间作用交叉明显，太沙基极限平衡理论不再适用于螺纹桩极限承载力的计算.根据既有研究及《螺纹桩技术规程》，螺纹桩达到极限荷载时沿桩体外径呈圆柱形剪切破坏，如图8所示，图中、分别为圆柱剪切面上不同位置的极限切应力.此时螺纹桩的极限承载力计算方法如下：

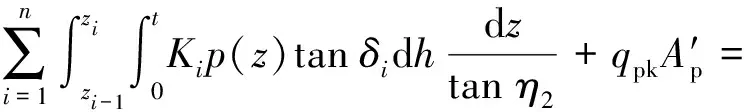
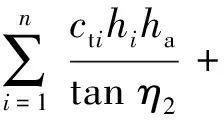
(23)

3 实例验证及参数讨论

某工地现场试验的桩型中，灌注螺纹桩的内径为400 mm、外径为560 mm、螺齿宽为80 mm、螺距为700 mm、桩长为8 m、宽厚比为1，干作业钻孔桩.现场试验场地工程地质条件如表1所示，所在土层为粉质黏土，土体重度平均为19 kN/m.

螺纹桩参数/>6且>，采用式(22)对螺纹桩承载力进行计算，螺纹桩极限端阻力标准值根据《建筑桩基技术规范》取 1 000 kPa.当取0时(即按M-C屈服准则计算)，螺纹桩承载力计算结果如表2所示.

可以发现，螺纹桩极限承载力理论值为 1 475.3 kN，螺牙提供的承载力达到了螺纹桩极限承载力的85%左右，而同外径混凝土圆桩极限承载力约为 1 100 kN，侧摩阻力占总承载力的77%.可以看出，螺牙的存在不但改变了桩体的承载特性，而且大大提高了承载力.同时发现，螺牙提供的极限承载力主要由土体、及桩体埋深决定，而滑块自重(非土体自重)引起的承载力仅占螺牙承载力的1%左右，因此忽略滑块自重对滑动面的影响，假定对数螺旋线的中点为点是合理的.

图9所示为螺纹桩承载力现场实测与理论值对比图，图中为桩所受荷载，为桩体沉降可以发现，螺纹桩沉降曲线可以分为3个阶段：直线增加段(包括与，下同)、过渡段及迅速沉降段，本文推导的极限承载力下限值正好位于过渡段与迅速沉降段的过渡点点附近.根据《建筑基桩检测技术规范》规定，对于缓变型-曲线，取沉降值达到40 mm时对应的荷载为极限承载力，对于陡降型-曲线，取拐点处荷载为极限承载力.本文中螺纹桩-曲线属于二者之间的过渡型，在判定极限承载力时徐春华等选择沉降40 mm时的荷载为极限承载力，分别为 2 000 kN及 2 100 kN，但是考虑到过渡点以后桩沉降速率明显过大，对工程的安全性极为不利.因此，本文认为选取点或者点与40 mm之间的某个点对应的荷载为极限承载力更为合适，即螺纹桩极限承载力在 1 500～2 000 kN之间.从图9中可以看出，当从0增大到1时，本文方法推导的螺纹桩极限承载力从 1 475 kN增加到了 2 187 kN，增幅约48%，说明极限承载力随着的增大而显著提高，计算过程中考虑该值的影响能更好发挥土体的承载潜能.当值取值合适时，本文方法计算结果与螺纹桩实际极限承载力将更加接近.

从前文推导中可以发现，除桩径等常规参数外，影响螺纹桩承载力的主要参数包括、及.图10所示为螺纹桩在=0时满足单独承载破坏条件下极限承载力随其关键参数的变化曲线，图中为参数尺寸.可以发现，对螺纹桩承载力影响最为明显，当从0.06 m增加到0.15 m时，螺纹桩承载力随之增加了约2倍，从 1 129 kN增加到了 3 096 kN，即较小螺牙高度的增加即可带来明显的承载力提升.然而，考虑到当螺牙高度较大时，螺牙悬臂端过长，容易产生冲剪破坏，而且螺牙下土体塑性区的发展受到限制，当螺牙高度超过到某一数值时，反而可能造成螺纹桩承载能力下降，这也是设计人员在螺纹桩设计过程中需注意的问题.

同时可以看出，螺牙厚度对螺纹桩承载力几乎没有明显影响，这是因为螺纹桩的承载力主要由螺牙下土体提供，而螺牙侧面面积较小，提供的承载力有限，故在螺纹桩设计过程中，在满足螺牙抗剪强度的前提下，可适当减小螺牙厚度，为螺牙间土体提供更多的塑性变形空间.当螺牙满足单独承载破坏条件时，随着螺距的增加，螺纹桩承载力先迅速降低.这是因为当螺距增加的时候，与螺旋线倾角相关的系数非线性降低，进而使得螺牙受力总面积迅速减小，极限承载力锐减.之后当螺距增加到一定范围时，承载力下降趋于平缓，这时螺牙提供的承载力仅占桩体的总承载力的一小部分，螺纹桩朝着混凝土圆桩的方向“退化”.因此，在保证螺牙下土体塑性区能充分发展的前提下，若要提高螺纹桩承载力，可适当减小螺距，使得螺牙下土体尽可能多的产生塑性破坏.

4 结论

针对螺纹桩承载机理不清、既有极限承载力计算不准确等问题，基于统一强度理论与太沙基极限平衡理论，推导了螺纹桩极限承载力计算公式，提出了螺纹桩不同模式下临界螺距的确定方法和极限承载力计算方法，并讨论了螺纹桩各参数对其承载力的影响，得出以下结论：

(1)螺纹桩极限桩承载力是同外径圆桩的 1.5～2倍，螺牙提供的承载力主要由土体黏聚力、内摩擦角及埋深决定，滑块自重贡献的承载力相对较小.

(2)统一强度理论参数从0增加到1时，螺纹桩极限承载力理论值约增大48%，取值合适时可以更准确地预测螺纹桩实际承载力，具有较好经济性、合理性.

(3)螺纹桩关键参数中，螺牙高度对其极限承载力影响最大，二者基本呈线性相关，而螺牙厚度对承载力基本不产生影响.

(4)在保证螺牙抗剪满足要求时，可适当增加螺牙高度，减小螺距，使得螺纹桩桩侧土体最大限度进入塑性变形，以提高螺纹桩极限承载力.