多层箔片超声焊接的摩擦能量耗散机理及影响因素研究
在金属超声波焊接中,焊头在一定的焊接力下压紧并抓持被焊金属箔片.焊接开始后,焊头沿水平方向发生频率为20 kHz的振动,振幅通常在20 μm左右.由于焊头上凸起的焊齿嵌入被焊金属箔片中,所以各层箔片会随焊头发生水平振动,接触面则产生剧烈的高频摩擦,并伴随温度升高.已有研究中,关于超声焊接的主要接合机理有两点:① 接触面附近的材料受到高温软化和声致软化的共同影响,在外载荷作用下发生塑性变形,进而形成机械嵌合;② 高温加快了金属原子的运动速率,相邻被焊箔片之间原子互相扩散,形成原子键合.在此过程中,温度始终未达到金属的熔点,因此非常适合焊接多层、薄片和异质金属.例如,在锂电池的极片和极耳连接、太阳能电池以及微细电子元件的制造中均有广泛应用.但是,由于超声能量自上至下传递并逐层衰减,当焊接对象层数较多时,各接触面的受载情况、摩擦行为以及各界面摩擦耗散能量差异显著.接触面的摩擦耗散能量直接影响接触面的产热和材料软化,不一致的摩擦能量耗散会导致各界面的固相连接程度不同,无法达到较高的焊接质量一致性.因此,有必要研究多层箔片超声焊接过程中各界面的受载状态和摩擦行为,分析各接触面的摩擦能量耗散情况,为工艺优化和调控提供理论依据.
根据上述过程,建立反冲质子磁谱仪中子能谱测量的带电粒子输运计算模型和程序。反冲质子磁谱仪性能模拟流程,如图2所示。
粗糙接触面滑动摩擦能量耗散的研究表明,接触面的摩擦能量耗散与法向载荷(焊接力)、切向载荷(超声振动)均存在显著相关性.郭利等将黏着剪切强度引入分形理论,利用有限元研究了界面滑动速度、法向载荷对摩擦能量耗散的影响,结论表明法向载荷的增大会增加能量耗散,而切向滑动速度会影响界面黏着效应,间接影响能量耗散.在超声焊接中,焊接力通过焊齿加载在试样上表面,各接触界面上出现集中分布的法向压应力,随后焊头产生切向的超声振动,带动最上层的试样发生切向运动,并通过试样间的相互摩擦力将切向运动向下传递.在此过程中,两种载荷在多个接触面呈现不均匀的分布,使得各接触面的摩擦行为变得复杂.且由焊齿产生的应力集中会使粗糙弹性体发生退让接触,载荷作用位置以外的弹性体会发生翘曲,进而分离,将影响接触面的摩擦状态,需在摩擦能量耗散的计算中给予考虑.根据Cattaneo-Mindlin接触理论,法向加载在引起接触面积改变的同时,也会使接触界面上形成切应力,接触界面的部分区域的切向力大于最大静摩擦力,将发生相对滑移;部分法向受载较大的区域,切向力小于最大静摩擦力,处于黏结状态,接触界面各处所能承受的最大静摩擦力由此处的法向应力和摩擦因数决定.多数学者采用有限元仿真法(FEM)研究接触界面的摩擦行为.Ahn等初步研究了循环载荷下两弹性体的单一接触界面黏结-滑移状态转化规律,利用FEM模拟了法向载荷循环加载、卸载下的接触界面摩擦行为,将接触界面分为黏结、滑移、分离三类区域,并且分析各区域面积随载荷的变化.Lee等进一步引入切向的循环力载荷以模拟超声波焊接过程中的金属箔片受力状态,利用FEM对比分析不同法向力、切向力组合下的界面黏结、滑移区域改变以及能量耗散情况,发现法向载荷对接触界面的摩擦能量耗散有显著影响.在超声马达研究中,Qu等利用MATLAB对界面黏结-滑移特征进行建模,仿真分析超声马达中的高频摩擦行为.但目前研究的对象集中于单一接触界面,被抽象为弹性体和刚性体接触,没有考虑塑性变形引起的接触状态变化.而在多界面摩擦中,各接触面上的黏结-滑移状态存在复杂的动态变化,仍有待进一步研究.
本文采用FEM对多层金属箔片的超声波焊接过程进行数值仿真研究.首先,建立多层金属箔片受法向、切向综合载荷作用下发生摩擦的简化二维模型,对比分析法向加载和切向循环加载时不同接触面的摩擦行为,仿真计算多种载荷工况下各接触界面的黏结-滑移区域分布及转化规律.然后,利用 Python 和MATLAB对FEM结果进行后处理,提取、计算各接触界面的摩擦能量耗散及其在各界面中的占比,分析影响摩擦能量耗散和各接触面占比的因素,为多层超声波焊接的过程调控提供初步的理论支撑.
1 有限元建模
1.1 几何建模
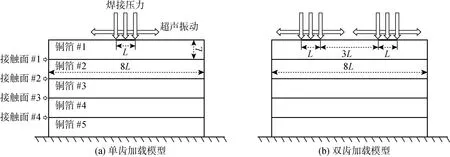
以5层0.2 mm厚的T2紫铜为研究对象,基于Abaqus 6.14建立二维力学模型.由于焊齿是重复结构,所以模型只需对部分焊齿下的局部区域建模,图1(a)为单齿加载的局部模型,分析加载宽度对金属箔片受载和摩擦状态的影响;图1(b)为双齿加载的局部模型,分析焊齿间距对载荷传递和摩擦状态的影响,并与单齿加载情况下金属箔片的受载和摩擦状态进行对比.模型中的各尺寸均参考实际焊接工况下焊头和金属箔片的尺寸,其中=0.2 mm.为提高仿真精度,金属箔片划分为尺寸为0.01 mm的均匀正方形细密网格,所有网格的网格类型均为CPS4R,共 16 000 个,每个接触界面上均有161对在初始时刻重合的节点.分析接触界面上节点的应力、位移、分离状态和滑移状态,并以此计算分析各界面的摩擦能量耗散.
一是把自己的思想装进别人的脑袋,二是把别人的钱装进自己的口袋。前者成功了叫老师,后者成功了叫老板,两者都成功了叫老婆。
1.2 材料及接触属性
考虑室温下材料的弹性和塑性属性:前者用弹性模量()和泊松比()定义,其中=129 GPa,=0.33;后者需要同时考虑应变强化和应变率强化特性,采用Johnson-Cook(J-C)模型,定义为
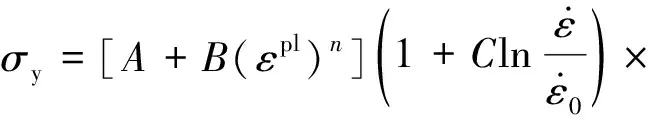
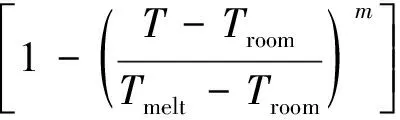
(1)
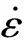
双齿加载时,接触面的压应力存在两处峰值,分别对应两齿的中心位置,如图6所示.和单齿加载相同,随着远离加载区域,压应力逐渐减小,但是在接触面的中心位置,压应力仍大于0,说明此处未出现界面分离,且3种载荷情况下,除了接触面#1在=±0.75 mm处出现了分离区域,其余各接触面均未出现分离现象.接触面积大小受法向载荷影响,随着法向载荷的增大,接触面#1的退让接触现象愈加明显,实际接触面积减小,下方各接触面的实际接触面积有增大趋势.

采用“面对面接触”设置接触面.外载荷自上至下传递,因此将每个接触对中的上表面设置为接触主面,下表面设置为接触从面,各接触面均为“硬接触”,并允许界面在接触后发生分离.采用恒定的摩擦因数反映粗糙界面,参考Lee等的研究结果,将铜箔之间的摩擦因数设为定值0.3;接触面中,并非所有区域都发生滑动摩擦,而是存在部分“黏结”区域.接触面各处的黏结-滑移状态可通过该处材料的屈服状态判断.若接触面上某微元发生屈服,则切向加载会使其产生塑性变形,位移为0,因此该处的接触面处于“黏结”状态;反之,若某处的材料未发生屈服,切向加载会使其发生滑动,则该处接触面处于“滑移”状态.材料的屈服状态可根据Von-Mises屈服准则判断:
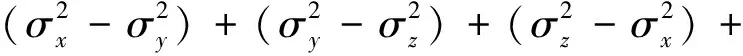

(2)
式中:下标int表示第个接触界面对应的能量或功率.

(3)
①过流标准确定。泄流渠的过流标准根据下游的防洪标准、现场施工能力、上游的库容大小和上游水位的上升趋势等因素确定,在保证下游安全的前提下,应尽可能选用较大的过流流量,以尽快降低湖内水位并减少水量。
综上所述,采用PS联合BiPAP治疗NRDS患儿 后,可有效提高临床疗效并降低不良反应发生率,并可有效改善患儿血清中TGF-β1及BMP-7水平。但本研究临床样本数较少,并未对患者长期疗效进行追踪。
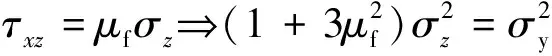
(4)
式中:为接触面的摩擦因数.
根据上述推导,若接触面的某处应力满足:

(5)
则该处未发生屈服,处于滑移状态.若接触面的某处应力满足:

(6)
则该处发生屈服,处于黏结状态.
1.3 外载荷设置
模型主要考虑法向的焊接力加载和切向的超声振动位移加载,两者均通过焊齿加载于顶层板的上表面,加载面积等于焊齿顶部面积,在模型中为顶面中间位置宽度为的区域(见图1).其中,焊接力沿接触面的法向,加载区域的线均布载荷设置为20~60 N/mm,对应加载区域所受的面均布载荷为 100~300 N/mm,实际工况下的焊接力为720~2 160 N;超声振动沿接触面的切向,均匀施加在与法向载荷相同的作用区域,超声振动可用正弦函数表示,角频率为2π,正弦振动的幅值参考超声焊接参数,设置为23 μm.仿真共设置两个加载步,分别进行法向加载和切向加载.第一个分析步时长设置为=1 s,在该分析步中,焊接力从0开始线性增大,在分析步结束时达到最大值,表示为

(7)
式中:为焊机设定的焊接力;为加载步1内的时刻.在第二个分析步中,法向压力保持恒定,切向载荷开始施加,焊头的横向位移可表示为
=sin 2π
(8)
式中:为振幅最大值;为加载步2内的时刻.
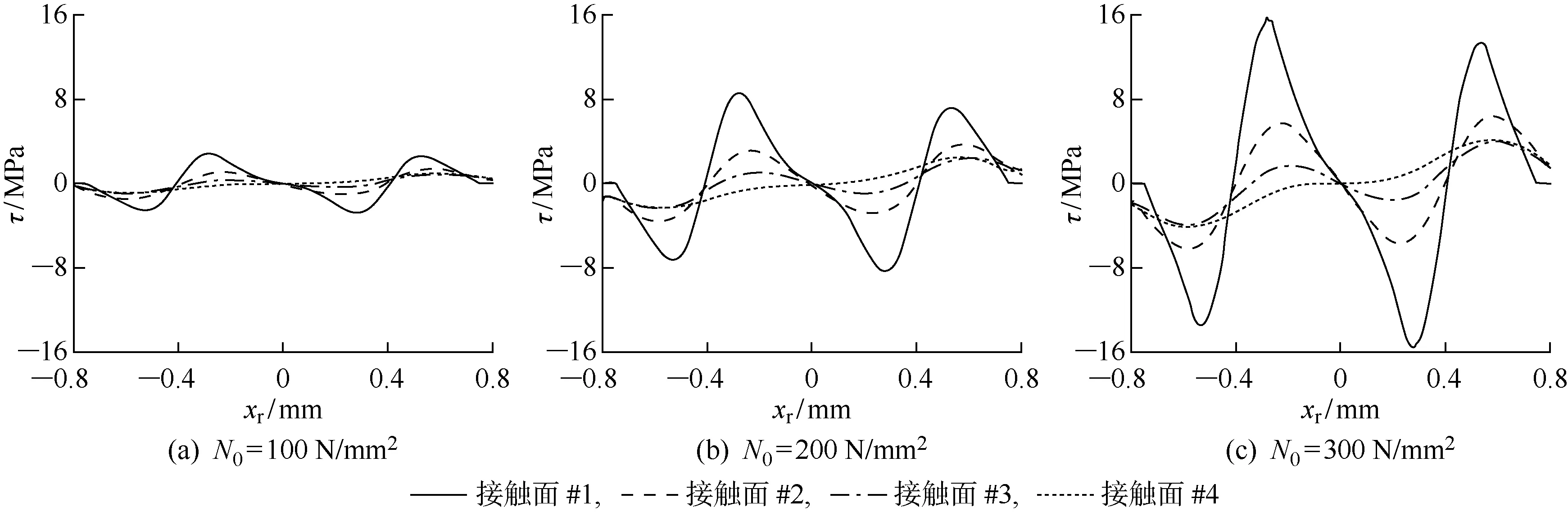
法向载荷集中加载在顶层板上表面的中心区域,引起接触界面的变形,并在接触面上产生切应力.图7为单齿加载状态下,=1 s时刻的接触面切应力分布.各接触面中心位置的受力对称,所以=0;随着远离接触面中心,切应力逐渐增大并在某处达到峰值,此后便不断减小至0,两侧=0的位置对应实际接触区域的边界.切应力的绝对值关于位置零点对称,峰值位置随着接触面靠下而向接触面的外侧移动.
加载曲线如图2所示.其中,为时间.最下层金属箔片在实际工况下与带有焊齿的基座接触并被基座抓持,在整个焊接过程中不发生切向位移,因此本模型中限制最下层板下表面节点的6个自由度为0.模型的增量步设为 0.031 25 s,即两个分析步中各均匀地分布着32个增量步.

2 仿真数据处理
2.1 黏结-滑移状态判断
在Abaqus的后处理过程中,可通过提取各节点的COPEN状态量,表征从面节点相对于主面的分离距离;提取各节点CSLIP状态量,表征从面节点相对于主面的滑移距离.通过提取各从面节点在每个增量步的两个状态量,即可计算并判断各时刻节点的黏结-滑移状态.基于Python 2.0,批量提取大量节点数据,主要提取每个增量步下,所有从面节点的COPEN和CSLIP数值,对相邻增量步的数据作差可以获得相对位移增量Δ和Δ,从而判断接触对所处状态.
式中:Δ为微元的面积,在本模型中指各单元的宽度.任意时刻总的摩擦能量耗散为
随着我国社会及经济的不断发展,商品外包装已经不再是单纯的包装作用,还应能通过商品外包装体现出商品自身的文化特质、质量特点等,进而确保这些商品能更好的在市场上占据一席之地。陶瓷在现代酒类包装设计中的应用将能更好的提升商品包装的价值。使用陶瓷作为酒类产品包装容器,消费者不需要将商品包装作为废品进行处理,陶瓷器具本身具备非常高的艺术欣赏价值。结合这些内容来说,除了提升商品质量之外,保证商品外包装的价值和品质也是非常重要的,因此,在现代酒类包装设计过程中,相关设计人员应能将陶瓷器具及陶瓷元素等灵活的应用起来。
Δ,=,,u-,,d
(9)

(10)
Δ,=,,u-,,d
(11)
具体判定依据可参见表2.

2.2 黏结-滑移状态图
为更直观地展示接触面的黏结-滑移转化规律,借鉴文献[19]的表示方法,绘制各界面的黏结-滑移状态图.图3为单齿加载在=100 N/mm时,最上层接触界面的黏结-滑移状态图.图中对应了法向加载分析步1 s的时间,为从面上节点的相对位置,零点为从面的中心位置;当前节点的状态包括:① 黏结状态,节点和主面接触且没有相对滑动;② 向右滑动状态,该节点接触主面且偏离原始位置向右发生滑移;③ 向左滑动状态;④ 分离状态,该节点未接触主面.

2.3 摩擦能量耗散占比
在接触界面摩擦因数恒定的前提下,界面上各处摩擦做功的功率主要由该位置的局部法向压力()、切向相对滑动速度()和决定模型中,节点任意时刻的摩擦做功功率为
1)γNa/γCl系数。γNa/γCl系数为地下水的成因系数,标准海水的γNa/γCl系数为0.85,低矿化度水的γNa/γCl系数大于0.85,高矿化度的γNa/γCl系数小于0.85[12]。由榆林市矿区离子系数统计表可知,γNa/γCl系数大于0.85的数量有31个,γNa/γCl系数小于0.85的数量有11个,说明榆林市矿区42个水样中绝大部分样品的TDS均较低。这主要是因为榆林市矿区潜水主要接受大气降水补给,排泄至周边河流的径流路径短,滞留时间短,水量交换循环积极,更替较快。
f,=,,Δ
(12)
定义,,u和,,u分别为第个增量步第个接触对从面节点的和向位移,,,d和,,d分别为第个增量步第个接触对下表面节点的和向位移,则

(13)
在Abaqus仿真软件中,可通过ALLFD状态量提取模型整体任意时刻的摩擦能量耗散值,但无法分别获取各接触界面的独立值.由下式可知,当摩擦因数为定值时,各节点的局部摩擦能量耗散正比于局部压力和滑移速度的乘积,分别计算获得各接触界面任意时刻的摩擦做功功率比率,可表示为


(14)
式中:、、和、、分别为微元所受的3向正应力和切应力在超声波焊接中,外载荷主要包括焊头向的压紧力和向的超声振动,因此接触面上各处仅受向的压应力和平面的切应力,则式(2)可简化为
实验教学是高等工程教育中的一个重要环节,对培养学生的动手能力、加深学生对知识的理解有着不可替代的作用。在“3+4”中职-本科衔接的课程体系中,实验教学内容和模式的衔接是至关重要的一环。我校机械工程学院从2017年开始接收中职转段学生。这部分学生的理论基础知识薄弱,所以要着力培养提高他们的动手能力和实践能力,提高专业素养,激发学生的学习兴趣和主动性。强化工程意识,使学生具有扎实的实践技能和创新能力。因此在这部分学生的人才培养方案中强化和加大了实践教学环节,目的使学生从基础知识到创新思维等各方面得到全方位的培养和提高。为此课题组着力进行了以下方面的实验教学改革:
每个增量步的时间极短,可认为在每个增量步中系统均处于准静态,各节点的摩擦能量耗散功率保持恒定,因此各接触界面的总摩擦能量耗散比率可表示为
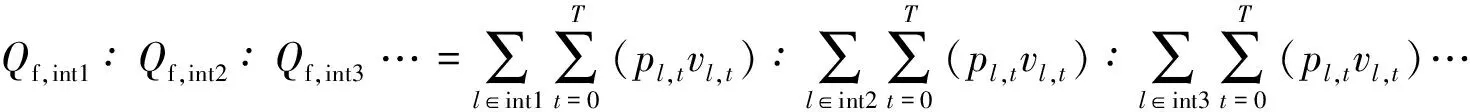
(15)
在进行后处理时,首先利用Python提取各接触对从面上的每个节点在每个增量步下的,值和,值,其中,可以通过时刻与-1时刻切向滑移距离计算得到,即,=,-, -1随后利用 MATLAB 计算得到每个时刻下各界面摩擦能量耗散功率的比率,以及时刻之前各界面摩擦能量耗散的比率.
3 分析与讨论
3.1 有限元仿真模型验证
通过实验获取5层铜箔的焊接变形,以验证模型的准确性.实验用铜箔为0.2 mm厚的T2紫铜,上下表面均镀有2 μm镍,镍镀层可在微观照片中清晰地显示各接触位置.实验用焊头由4×9阵列分布的金字塔状焊齿组成,如图4(a)所示.焊机压力设置为250 kPa,通过压力传感器测量,实际作用在试样上的焊接力为 1 642 N,振幅为23 μm,焊接时长为0.4 s.在焊头的压痕处,沿超声振动方向切割焊接试样,制备成金相试样,试样和切割位置如图 4(b)所示.
在D-Met组中,以2.5 mmol/L组的生物膜总生物量最高,分别于10、25、50 mmol/L组相比均有统计学差异(P<0.05),而10、25、50 mmol/L组间相比则无统计学差异(P>0.05)(图2a);各浓度组的生物膜清除率为:10、25、50 mmol/L组>2.5 mmol/L 组(P<0.05)(表1)。
在模型中带入高温软化后的材料属性,以仿真焊接最终时刻的金属箔片变形,具体属性选择参考文献[22],仿真模型中的焊接力选择和实验保持一致.选择焊齿下方各层铜箔的减薄率为比较对象,如图4(c)所示.可知,实验和仿真中各层铜箔的厚度基本一致,表明仿真模型可以真实地反映焊齿下方各层铜箔和接触面的应力以及应变分布情况.

3.2 接触面载荷传递规律
提取法向载荷加载结束时刻,即=1 s时各界面的压应力()和切应力(),以分析载荷在多界面中的传递特征.单齿加载时,接触面中心压应力最大,向两侧不断减小,并在滑移区域和分离区域的边界处达到0,越靠下的接触面压应力峰值越小且接触面积越大,如图5所示.

是的,我把持不住了。男女间的那些事,我明白,又不明白,现在,就要捅破那层窗户纸,知道女人是怎么回事了,就在这紧要关头,我爆炸了。爆炸过后,我舒畅了,疲倦了,也知道自己丢人丢到家了。

充分提供情节背景下的学习是最有效的,语文学习的外延与生活的外延相等,生活的范围有多大,学习语文的范围就有多大。我们常常说的“生活即语文”正是这样的道理。

双齿加载时,各界面的切应力分布发生变化,如图8所示.两处加载位置沿界面中心对称,因此切应力的绝对值关于零点对称,但是切应力的绝对值不再关于载荷施加中心(=±0.6 mm)对称,而且切应力峰值由2个变为4个.以左侧加载区域为例,从=-0.8 mm至接触面中心的切应力是由左侧加载引起的,然而在=-0.6 mm处,≠0,这与单齿加载不同,说明在双齿加载下,两处法向加载所引起的变形会产生相互影响,导致加载区域正下方的接触面发生相互滑动;并且由于加载区域左侧为自由端,所以左侧的切应力峰值显著低于右侧的切应力峰值.
此外,压应力和切应力遵循库伦摩擦定理,因此式(3)可变换为
3.3 接触面的黏结-滑移状态转化
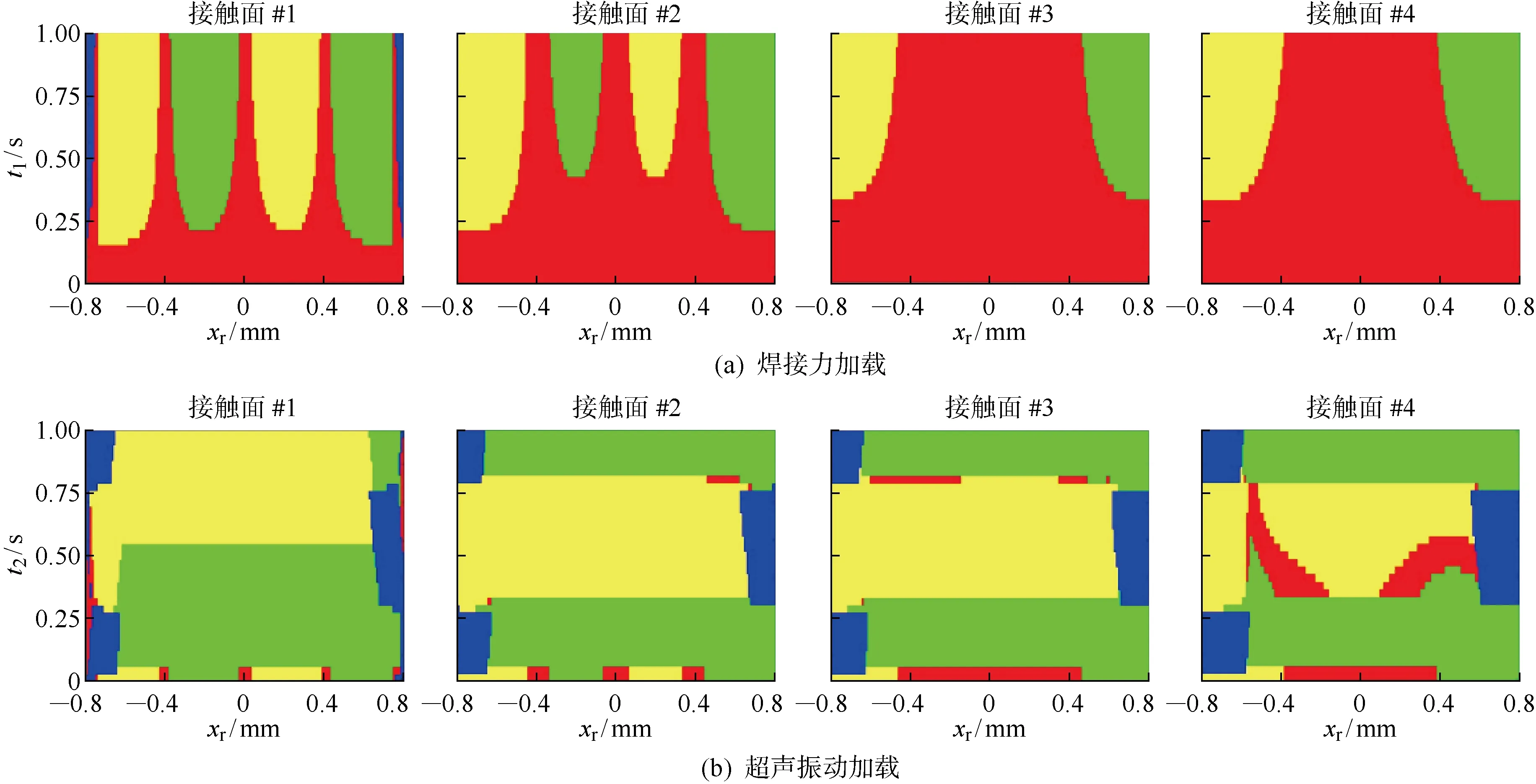
根据前文后处理方法,制作=100 N/mm时的界面黏结-滑移转化图,如图9所示.在单齿加载时,4个接触面上均出现明显的退让接触现象,并且在切向加载和法向加载阶段,各接触面的两侧均存在分离区域.此外,上层箔片接近焊齿、变形量更大,导致上层接触面的分离区域也明显更大,在切向加载阶段更为明显,从图中可以明显看出下层接触面的滑移面积更大.当切向载荷方向改变时,滑移区域的滑动方向随之改变,并且滑移区域的位置也随着载荷方向产生位移,在下层界面中,滑移区域的位移更大.

对接触面的滑移面积进行定量分析,分别提取不同法向载荷下各接触面的滑移面积占总面积的比率(),如图10所示.随法向载荷的增大,接触面的最大静摩擦力增大,各接触面的滑动面积减小.并且由于退让接触现象,法向载荷增大还会导致各接触面的实际接触面积减小,从而进一步减小滑移面积.其中,最上层界面的退让接触最为明显,因此滑动面积的减小量最大.
本文主要分析了双绕组电力变压器集总参数模型,构建了串联阻抗支路矩阵和并联导纳支路矩阵,再基于基尔霍夫电流和电压定律来获取支路电流与节点电压之间的关系;同时分析了变压器绕组径向变形和轴向位移故障时的主要影响参数,以期为后续系统研究变压器绕组故障提供相关的理论基础。
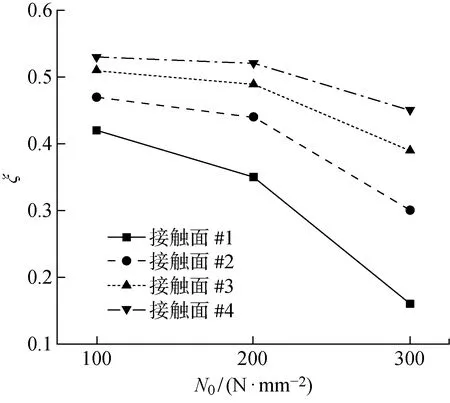
图11为=100 N/mm、双齿法向加载时的接触面黏结-滑移状态转化图.由于总加载宽度增大,所以接触面的分离面积均减小,仅出现在加载结束时接触面#1的两侧.在法向加载阶段,接触面 #1和#2上分别出现了3个黏结区域,其中左右两侧的黏结区域出现在载荷正下方,其形成机理和单齿加载时相同;而上层接触面的退让接触现象明显,因此接触面#1和#2加载区域的两侧均出现滑移区域.但接触面的中心位置切向受力平衡、=0,接触面中心出现了第三个黏结区域.在滑移阶段,接触面#1滑移方向的转变在=0.5 s附近,而其余3个接触面分别存在2次滑移方向转变,可以认为接触面#1的滑动与其余3个接触面存在一定相位差.
3.4 接触面的摩擦能量耗散
基于仿真得到的接触面节点相对滑动速率和法向压应力,计算各接触面摩擦耗散能量占比,如图12所示.其中,≤1 s为焊接力法向加载阶段,>1 s为切向位移加载阶段.在法向加载阶段,接触面的摩擦均来源于退让接触带来的滑移,接触面#1由于直接接触焊齿,其变形量和切应力最大,所以接触面#1的摩擦能量耗散占比最高.随着界面靠下,摩擦能量耗散的占比逐渐变小,与3.1节中的结果相符.在切向加载阶段,接触面#1的摩擦能量耗散占主导地位,其余3层摩擦能量耗散几乎为0,但随着法向载荷的增大,接触面#1的摩擦耗能占比减小.结合3.2节中的结果,可知当法向载荷增大时,在切向加载阶段,接触面#1的滑移区域减小但分离区域增大,而其余各界面滑移面积的变化并不明显,以上原因共同导致接触面#1的摩擦能量耗散相对较小.
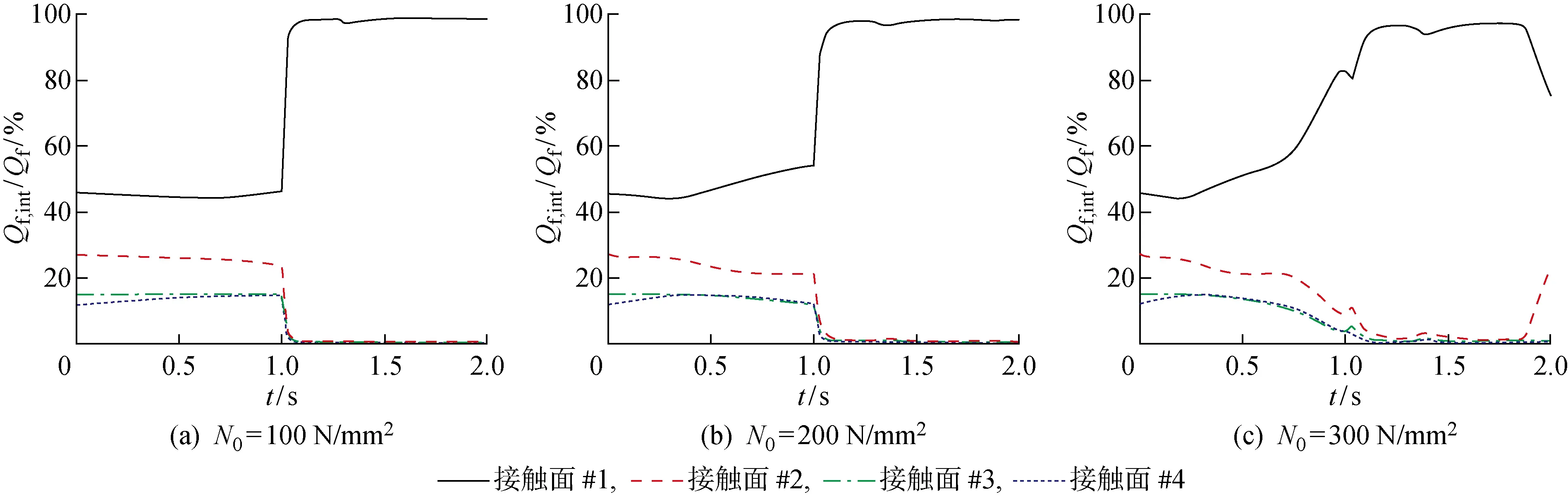
根据分析,受集中加载的影响,随着法向载荷的增大,单齿加载的接触面发生较大变形,导致分离区域增大,进而使接触面#1的摩擦能量耗散占比减小.但是双齿加载的载荷分散、加载面积大,接触面的分离面积几乎为0,因此各界面摩擦能量耗散占比受法向载荷大小的影响减小.如图13所示,随着法向载荷增大,各接触面摩擦能量耗散占比几乎不变.然而各接触面实际的摩擦耗散能量在不同法向载荷下却存在显著差异.提取并绘制切向加载阶段摩擦能量耗散随时间增长的曲线,如图14所示.可知,随法向载荷的增大,任何时刻的摩擦能量耗散均随之增大,较之=100 N/mm时,=200 N/mm和=300 N/mm时的摩擦耗散能量分别提高了0.499 mJ和0.307 mJ;而在双齿加载工况下,=200 N/mm和=300 N/mm时的摩擦耗散能量分别提高了0.526 mJ和0.509 mJ,均大于单齿加载工况.各接触面的实际摩擦耗散能量均增大,各接触面的能量比值变化不明显.

在相同法向载荷下,对比单齿和双齿两种不同工况的摩擦耗散能量,如图14所示.双齿加载工况下的摩擦能量耗散在任意时刻均大于单齿工况,并且两者之间的差值随着法向载荷的增大而不断增大.当=100 N/mm和=200 N/mm时,双齿下的摩擦耗散能量较之单齿加载时分别提高了0.006 mJ和0.032 mJ,升高比率为1.15%和3.12%;而当=300 N/mm时,双齿下的摩擦耗散能量提升最大,为0.233 mJ,升高比率为17.4%,这是由于单齿加载状态下各接触面存在明显的退让接触、边缘位置发生分离(见图9),而双齿加载则几乎不存在上述问题(见图11),所以在较大法向载荷下,双齿加载能使更大的分离区域发生接触,摩擦耗散能量的增量也更大.

3.5 摩擦能量耗散的影响因素分析
在多层超声焊接中,最上层接触面的摩擦耗散能量占比过大会导致下层接触面得不到足够的超声能量形成接合,因此提高整体的摩擦耗散能量,特别是提高下层接触面的能量占比是工艺优化的主要方向.分别从改变焊齿尺寸和分布,以及改变法向载荷大小两个方面讨论摩擦能量耗散的影响因素和改进思路.
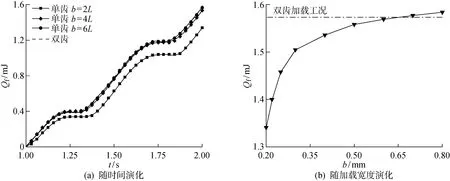
由上述分析可知,双齿加载时接触面的分离区域被消除,应力分布也更均匀,使得各界面的摩擦能量耗散量增大,该效果接近于增大单齿加载区域面积.通过增大单齿加载区域的面积,对比摩擦耗散能量值可知,随着加载面积的增大,切向加载阶段各时刻的摩擦耗散能量均有所增大,如图15(a)所示.其中,为加载宽度,=6为双齿加载时的齿间距.并且在=0.6 mm时,摩擦耗散能量大小接近双齿加载.建立单周期总摩擦耗散能量与加载宽度的函数,可知,摩擦耗散能量和加载宽度正相关,并且随着加载宽度的增大,摩擦耗散能量的增长速度减小,如图15(b)所示.图中,双齿加载的摩擦能量耗散与单齿加载=065时基本相同,可知当加载区域的边界位置相同时,双齿分散加载和单齿加载不会对摩擦能量耗散产生影响.考虑超声波焊接实际情况并结合上述结论,可知当焊齿间距足够近,则接触面不会产生退让接触,此时具有焊齿的焊头与平面焊头具有相同的摩擦耗散能量.并且配备焊齿的焊头可以极大地减小顶层金属箔片的滑动,将更多超声能量向下传递.但是在多层焊接中,则需要利用退让接触带来的摩擦能量耗散占比向下偏移趋势,提高接触面的退让接触程度.
焊接力对系统整体的摩擦能量耗散规律和各界面占比均有显著影响,因此在超声振动阶段,对焊接力增加一个正弦项,从而调节摩擦能量耗散及其在各界面中的分布情况:
按照多年的培训新进检验员的实践经验,我们把新进检验员一年的岗前培训和成长过程分为科室社会化适应期、胜任力扩大期、工作丰富化期、逐渐独立期四个阶段,科室主任和带教老师通过目标管理的方式,于四个阶段分别有意识地对新进检验员进行培养。
前文也提到事件营销具有深度传播性,一旦形成热度,便容易成为人们经常讨论的话题。一般的“事件”,关注的人群是局限的。人们通常都是关注自己关心的东西,例如饭圈女孩关注的都是明星,爱好运动的运动迷关注的当然都是各大体育赛事等,人们不会花费心力在不感兴趣的事上。但事件营销带来的热度会使得传播的人群不再仅限于专注于该类新闻事件的群体,从而形成二次传播。由此,对品牌形象在消费者心中的固化,培育品牌忠诚有很重要的影响。
=(1+sin 2π)
(16)
式中:∈[0, 0.4]为正弦项幅值.
通过调节超声振动加载阶段的焊接力,同样会对摩擦能量耗散产生显著影响.随着值增大,一个振动周期内的总体摩擦能量耗散呈现先减后增的趋势,如图16(a)所示.当没有正弦振荡加入时,系统的摩擦耗散能量最大,随着值增大,系统总摩擦耗散能量快速减小,并在=02时,达到最小值;随后,随着值增大,总摩擦耗散能量再次缓慢增大.附加正弦项的焊接力对各接触面的滑移面积占比同样有显著影响,且存在和总摩擦耗散能量相似的规律,如图16(b)所示.在=0时,接触面#1的摩擦能量耗散占主导地位,随着值增大,接触面#1的摩擦能量耗散占比快速减小,同时接触面#2的摩擦能量耗散占比增大,并在=02处同时达到极值;随着值继续增大,接触面#1的摩擦耗散能量占比缓慢增大,而接触面#2的摩擦耗散能量占比开始减小.

4 结论
(1)在法向加载阶段,各界面均会出现退让接触,在接触面上分别出现黏结、滑移和分离现象,其中,接触面分离现象在单齿加载时较为显著,双齿加载时则几乎消失;在超声振动加载阶段,各接触面的滑动面积增大,下层接触面的滑移面积明显高于上层接触面.
(2)法向载荷大小对各接触面的滑动摩擦面积和摩擦耗散能量均有直接影响,法向载荷增大会提高总摩擦耗散能量,减小各界面的滑移面积;单齿加载时,上层接触面的滑移面积减小量大于下层接触面,接触面#1的摩擦耗散能量占比有所减小.
(3)单齿加载时,增大加载区域宽度可以提高总摩擦耗散能量;双齿加载时,增大两齿间距也可以提高总摩擦耗散能量;当单齿加载的宽度等于双齿加载时的齿间距时,两者的总摩擦耗散能量相近.
(4)对法向载荷增加正弦变化可以提高下层接触面的摩擦耗散能量占比,但是会降低摩擦耗散能量总量;该变化受正弦项幅值影响:当=0时,总摩擦耗散能量最大,接触面#1的摩擦能量耗散占比最高;当=0.2时,总摩擦耗散能量最小,接触面#2的摩擦能量耗散占比最高.

