同步实施的相邻基坑相互作用机理

随着我国城市化进程的不断加快和地下空间的大规模开发利用，基坑工程作为城市建设的重要手段，数量越来越多，面积越来越大，施工越来越复杂.一方面，由于基坑数量增多，城市用地紧张，许多基坑不得不与其他基坑相邻；另一方面，为了减小超大基坑的变形及其对周围环境的影响，需要将超大基坑划分为相邻基坑进行施工.因此，相邻基坑工程日益增多.许多相邻基坑工程往往采用同步实施的施工方法，从而加快建设进程，而同步实施的相邻基坑的受力变形特性与单个基坑存在较大差异，这一问题引起了学者们的广泛关注.

理论研究方面，岳树桥等采用薄层单元法，推导了相邻基坑间有限宽度土体的主动土压力计算公式.陈小雨等根据极限平衡理论，得到了相邻基坑相互影响的临界间距表达式.现场实测方面，Zeng等根据监测数据，对相邻基坑的围护墙水平位移、墙顶垂直位移及地表沉降等变形特性进行了研究.李成巍等则提出了相邻基坑同步实施的总体思路和技术措施，并通过实测数据验证了方法的可行性和有效性.数值分析方面，李明广重点关注开挖方式和基坑间距等因素对相邻基坑的影响.叶建峰等对相邻基坑的失效机理和破坏模式进行了分析.尽管许多学者从多种角度对同步实施的相邻基坑展开了研究，但相邻基坑的相互作用机理尚不清晰，阻碍了工程实践的发展.

本文采用数值方法，首先通过工程实例对计算方法进行验证，在此基础上建立起基于小硬变硬化(HSS)本构模型的相邻基坑理想模型，通过对比单个基坑模型和不考虑墙土摩擦的相邻基坑模型，得到了同步实施的相邻基坑的受力变形特性.基于土拱效应原理，揭示了相邻基坑相互作用机理，并研究了基坑间距对基坑受力变形的影响规律.

1 计算方法验证

1.1 工程概况

在上海世界博览会B片区地下空间工程中，基坑C1和基坑D被一条道路分隔而形成相邻基坑，剖面如图1所示.基坑C1的开挖深度为15.45 m，其地下连续墙长31.9 m，厚0.8 m；基坑D的开挖深度为18.50 m，其地下连续墙长40.9 m，厚1 m.基坑C1和基坑D分别设置3道和4道钢筋混凝土支撑，并分4层和5层开挖.两基坑几乎同步实施，并在基坑开挖前中间道路的施工已完成.Zeng等对该工程进行了详细报道，本文不再赘述.

1.2 数值模拟

为了消除边界对基坑的影响，墙A至模型左侧边界的距离和墙D至模型右侧边界的距离均超过5倍开挖深度.围护墙和道路板采用板单元模拟.混凝土支撑采用点对点锚杆模拟.在Plaxis 2D中点对点锚杆无重度，所以未模拟立柱.钻孔灌注桩采用嵌入式梁单元模拟.混凝土的弹性模量取25 GPa，泊松比取0.2.为考虑汽车荷载、材料堆积荷载等因素的影响，在两基坑中间和基坑D右侧施加20 kPa的竖向荷载.

根据实际施工过程确定施工步：首先开挖基坑C1的第1层土，再开挖基坑D的第1层土，之后依次同步开挖两基坑的第2、第3、第4层土.由于基坑C1和基坑D为基坑群中的两个子基坑，两基坑在其第4层土开挖结束后受到了周围基坑开挖的显著影响，故本文不考虑基坑D第5层土的开挖.

1.3 结果验证

图2所示为分别位于墙A、墙B和墙D上的3个测点的实测数据与相应数值模拟结果的对比，图中为水平位移，C1-3表示基坑C1开挖第3层土，其余类似.由图2可以看出，数值模拟结果与实测数据整体吻合较好，验证了本文建模方法和模型参数的合理性和准确性.

当=05时，土体宽度进一步减小，由墙体不均匀变形引起的土拱效应进一步减弱，墙B上部向坑外的位移对土压力的影响越来越大，因此墙B上部所受土压力并未减小，反而因承受被动土压力而增大.在考虑墙土摩擦的情况下，由于基坑间距减小，坑间地表沉降增大，由墙土摩擦引起的土拱效应增强，所以开挖面附近墙B所受土压力减小，而当不考虑墙土摩擦时，墙B在开挖面附近所受的土压力增大.

2 理想模型及其变形特性

对于由墙土摩擦引起的土拱效应，Handy提出了小主应力拱迹线理论，墙后土体的应力状态可用图6(a)所示的莫尔圆表示.图中，为大主应力，为小主应力，为切应力，为水平正应力，为竖向正应力，为墙土摩擦角，为大主应力与水平方向的夹角.由此可知小主应力迹线为一条向下弯曲的曲线.对于由墙体不均匀变形引起的土拱效应，根据Handy的小主应力拱迹线理论，最后一道支撑处土体的应力状态可用图6(b)所示的莫尔圆表示.图中，为土体内摩擦角，为小主应力与竖直方向的夹角.由此可知大主应力迹线为一条凸向坑外稳定土体的曲线.因此，主应力旋转角能够直接反映土拱效应的变化.在最后一道支撑附近，上下土层之间发生土压力转移，主应力旋转明显，因此选择9 m深度处观察坑间土体主应力旋转角的变化，如图7所示.图中，为点到墙B的距离，为主应力旋转角，规定主应力顺时针旋转为正，逆时针旋转为负.由于主应力旋转角成中心对称，所以只取=(0～05)进行分析.

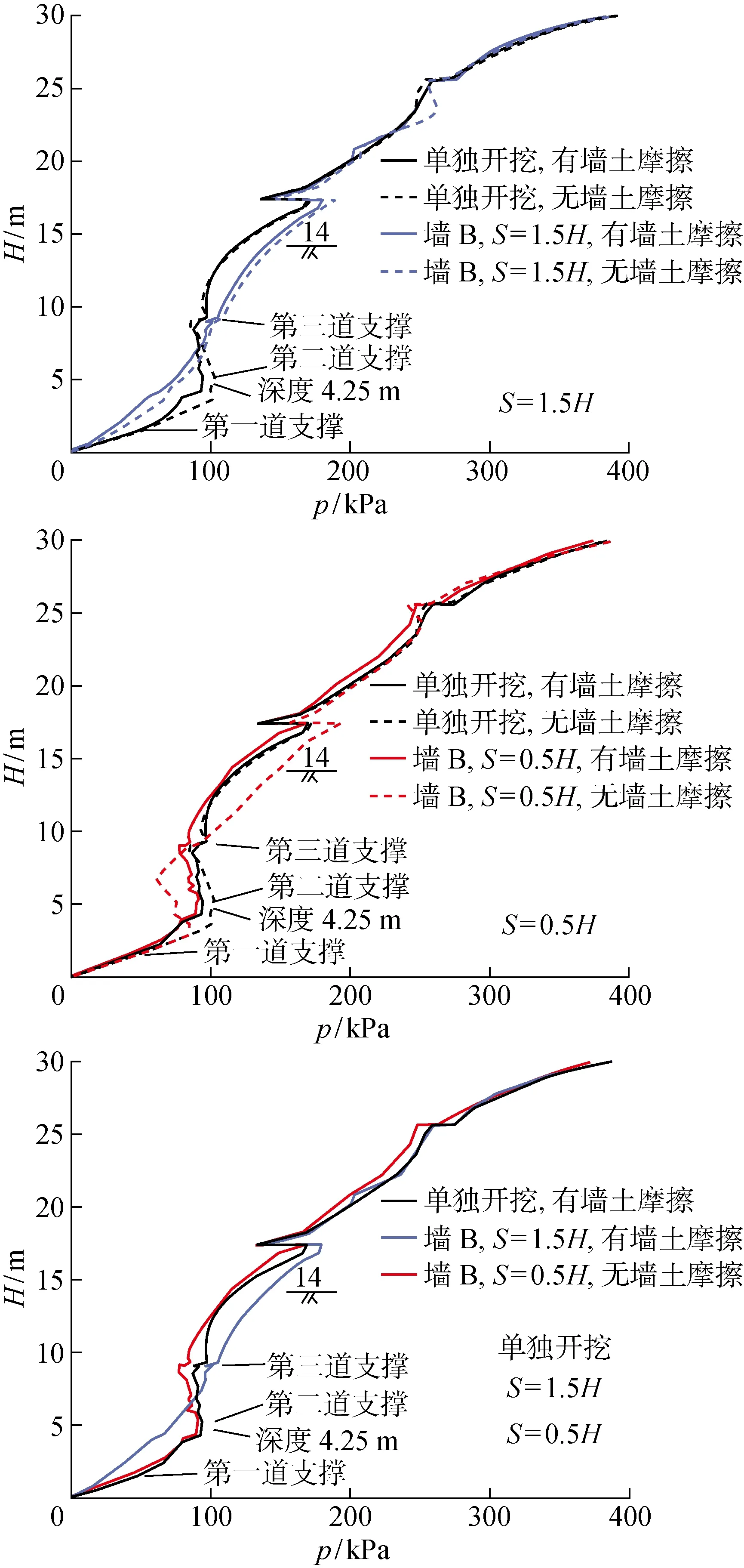
Zhang等认为同步实施的相邻基坑不存在相互影响的临界间距约为1.7，陈小雨等则认为土压力的临界间距约为2，墙体变形的临界间距约为3.基于此，本文选取单独开挖、=15和=05共3个代表工况分析基坑的受力变形特性.图4所示为开挖至坑底时围护墙的水平位移，规定向基坑内的变形为正，向基坑外的变形为负.当=15时，墙A和墙B的水平位移最大值均大于单独开挖时的水平位移最大值，墙A顶部向基坑内移动，墙B顶部向基坑外移动，从基坑变形的角度看，两基坑向中间倾斜.当=05时，墙A的水平位移最大值进一步增大，而墙B的水平位移最大值减小，并且小于单独开挖时的水平位移最大值，两墙的墙顶位移与=15时的墙顶位移大致相同.

经过不断优化调整，去年装置产出合格的HVIⅡ10号重质加氢基础油。8月，装置具备稳定生产重质加氢基础油的能力，在满足市场需求的同时，实现了装置产品多样化差异化。

3 相邻基坑相互作用机理

3.1 土压力分布

由图5(b)可知，当=05时，在考虑墙土摩擦的情况下，土压力并没有进一步向线性分布发展，而是回到R型分布.在不考虑墙土摩擦的情况下，墙B上部所受土压力减小，开挖面附近所受土压力增大.

图5所示为3个代表工况下围护墙所受土压力的分布图.由图5(a)可知，在考虑墙土摩擦的情况下，单独开挖时，围护墙所受土压力呈R型分布.当=15时，与单独开挖相比，墙B上部所受土压力减小，开挖面附近所受土压力增大，土压力分布由R型分布向线性分布发展.在不考虑墙土摩擦的情况下，单独开挖和=15时的土压力均大于相应的考虑墙土摩擦时的土压力.

图5(c)为在考虑墙土摩擦时单独开挖、=15和=05的土压力对比.可见，随着基坑间距的减小，土压力分布先由R型分布向线性分布发展，再回到R型分布.

3.2 土拱效应对土压力的影响

图9所示为水平位移最大值随间距的变化，图中为不同间距下的水平位移最大值，为单独开挖时的水平位移最大值.可知，随着基坑间距减小，墙B的水平位移最大值先增大后减小，墙A的水平位移最大值不断增大.两墙水平位移最大值的变化规律与其在14 m深度处所受土压力的变化规律基本一致.

当=15时，与单独开挖相比，作用在墙B上的土体宽度减小，导致土层之间的摩擦力减小，由墙体不均匀变形引起的土拱效应减弱，被支撑土体和开挖面附近土体之间的土压力转移减弱，所以土压力趋近于呈线性分布.在考虑墙土摩擦的情况下，土体中的部分应力向墙体转移，因此单独开挖和=15时的土压力均小于相应的不考虑墙土摩擦时的土压力.

利用AS-4光电分析程序对比赛的录像进行分析，特别是对每个运动员的弹跳参数进行测定。表2列出的是5名排球运动员跳跃的平均高度与最大高度的百分比关系，跳跃动作的参数选取比赛中的进攻、拦网、发球、传球四个技术动作。

一是实施意识领先方略，强化水安全意识。充分重视水在社会经济中的重要基础地位，提高水作为资源要素、环境要素、生态要素、安全要素的基本认识，统筹谋划水资源开发利用与社会经济发展。进一步落实领导责任，尤其是地方政府责任，把水安全责任落实作为干部政绩考核、选拔任用的重要依据。建立健全节水社会动员参与机制，充分利用各类媒体，全面客观介绍水资源危机、节水常识，保护水文化遗产，提高公众节水意识。高度重视和发挥非政府组织在水安全中的积极作用，营造企业履行社会责任的社会环境。

3.3 主应力旋转

根据实际工程建立的数值模型存在许多干扰因素，因此本文以上述模型为基础，通过适当调整参数建立如图3所示的理想模型.在该模型中，两侧边界为法向约束，底部边界为全约束.左右两基坑完全相同，宽度为100 m，开挖深度为14 m.分4层同步开挖，每层分别开挖2、4、4及4 m.设置3道支撑，3道支撑所在深度分别为1、5及9 m.围护墙深度均为30 m，厚度均为0.8 m，非相邻围护墙称为墙A，相邻围护墙称为墙B，基坑间距记为.为了研究相邻基坑相互影响机理，本文还建立了单独开挖的基坑模型，并且通过控制围护墙界面单元摩擦角为0°，建立了不考虑墙土摩擦的基坑模型.后文中若无特别说明，分析均针对考虑墙土摩擦的情况.

在考虑墙土摩擦的情况下，当=15时，紧靠墙B处墙土摩擦导致主应力顺时针旋转，主应力旋转角为正值；随着的增大，墙土摩擦作用减弱，土层之间的摩擦作用导致主应力逆时针旋转，因此在01范围内，主应力旋转角强烈变化，由正值变为负值；在01～05范围内，随着的进一步增大，上下土层之间的摩擦作用逐渐减弱，主应力旋转角逐渐减小为0°=05时，由墙土摩擦引起的土拱效应较强，主应力旋转角主要为正值且大致成线性变化不考虑墙土摩擦的情况下，=15和=05时，紧靠墙B处主应力旋转角明显减小，而=05时主应力旋转角依然为正，可能是因为受上部土体大主应力为水平方向(90°)的影响.

偏瘫性肩关节周围炎属于常见的骨科疾病之一，主要的临床症状为行动不便、剧烈疼痛等，男性患者人数多于女性患者人数，但是近年来，女性患者人数在逐渐提高，并且开始向年轻化方向发展，患者发病年龄主要在50岁左右[7-9]。目前，临床上尚未总结出引发肩痛穴平衡针灸的病因，这极大程度上增加了疾病的治疗难度，疾病发作机理如下：患者的中枢系统受到肩周炎的影响，导致患者的神经中枢功能出现了下降，肌肉出现萎缩且肌肉张力下降，在影响患者正常活动的同时增强患者的疼痛感。

4 基坑间距影响分析

建立多个不同间距的相邻基坑模型，研究基坑间距对基坑受力变形的影响.4.25 m位于第一道支撑和第二道支撑之间且靠近第二道支撑(见图5)，14 m 为最终开挖面所在的深度.取两处作为典型深度研究墙A和墙B所受土压力随间距的变化，如图8所示，图中为单独开挖时的土压力.可知，随着基坑间距的减小，墙B在4.25 m深度处所受的土压力先减小后增大，在 14 m 深度处所受的土压力先增大后减小.由墙体不均匀变形引起的土拱效应的减弱和由墙土摩擦引起的土拱效应的增强导致了墙B在两典型深度处所受土压力的变化.随着基坑间距的减小，墙A在4.25 m深度处所受的土压力略有增大，在14 m深度处所受的土压力先减小后略有增大，墙A所受土压力的变化则是两墙变形协调的结果.

土拱效应是影响土压力大小和分布的重要因素.文献[11]认为土拱效应是土工试验中最普遍的现象之一.基坑围护墙后也存在土拱效应.当围护墙由静止状态向主动极限状态发展时，墙后土体相对于围护墙和滑裂面向下运动，墙土摩擦角和土体内摩擦角的发挥导致应力重分布.此外，Hashash等发现，对于设置内支撑的柔性围护结构，墙体的不均匀变形和围护墙侧向刚度的变化，被支撑土体和其下方土体之间也存在土拱效应，支撑下方土体的部分应力会转移至被支撑土体.因此，单独开挖时围护墙所受土压力呈R型分布.对于围护结构为柔性的相邻基坑，在坑间土体中会出现两种土拱效应的叠加.

可将变化曲线大致划分为3部分：当≥25时，墙A和墙B水平位移最大值基本不变；当10≤<25时，两墙水平位移最大值均大于单独开挖时的水平位移最大值，但变化量较小；当<10时，水平位移最大值发生显著变化，并且与单独开挖相比，墙A水平位移最大值增大，墙B水平位移最大值减小.

5 结论

本文依托实际工程，采用数值模拟的方法，得到了同步实施的相邻基坑的受力变形特性，揭示了相邻基坑相互作用机理，研究了基坑间距对基坑受力变形的影响规律，得出以下主要结论.

另外，纸基地膜的纤维素材料具有一定的吸湿性能，不但具有调节土壤湿度的作用，而且空气湿度也有一定的调节作用，可以有效抑制大棚中因过度潮湿而带来的菌核病和灰霉病等病害的发生和传播。

语篇衔接与人际意义——以外媒一篇关于“网络战争”的新闻评论为例 ………………………… 戴祯琼（6.41）

(1)坑间土体中存在两种土拱效应，一种是由墙体不均匀变形引起的土拱效应，另一种是由墙土摩擦引起的土拱效应，两者共同影响作用在围护墙上的土压力.随着基坑间距的减小，由墙体不均匀变形引起的土拱效应减弱，导致开挖面附近土体向被支撑土体的土压力转移减弱.由墙土摩擦引起的土拱效应增强，导致作用在相邻围护墙上的土压力减小.

(2)可能偏差。对于精煤段，这两种旋流器5个粒级的可能偏差各有不同，但50～0.5 mm综合粒级的可能偏差，三产品重介质旋流器为0.022 kg/L，而主再选两产品重介质旋流器为0.033 kg/L，显然前者优于后者。对于矸石段，50～0.5 mm综合粒级三产品重介质旋流器的可能偏差为0.034 kg/L，主再选两产品重介质旋流器的可能偏差为0.035 kg/L，从各粒级的情况来看，除了13～6 mm粒级以外，前者的可能偏差均优于后者。

(2)在两种土拱效应的作用下，随着基坑间距的减小，作用在相邻墙体上的土压力先由R型分布向线性分布发展，再向R型分布发展.非相邻墙体水平位移最大值增大，相邻墙体水平位移最大值先增大后减小，两基坑向中间倾斜.

(3)水平位移最大值随基坑间距的变化可以分为3部分：当≥25时，相邻和非相邻墙体的水平位移最大值基本不变；当10≤<25时，与单独开挖相比，两墙水平位移最大值均增大，但变化量较小；当<10时，水平位移最大值发生显著变化，并且与单独开挖相比，非相邻墙体水平位移最大值增大，相邻墙体水平位移最大值减小.