城市物流无人机起降点布局规划研究

张洪海，冯棣坤，张晓玮，刘皞，钟罡，张连东

(南京航空航天大学，民航学院，南京 211106)

0 引言

自2020年新冠疫情爆发以来，无人机作为运输载具凭借无接触、全天候、高灵活性等独特优势在物流配送领域展现出强大的竞争力[1]。物流无人机起降点布局规划是构建城市无人机物流配送体系的重要环节，是实现大规模无人机物流的第一步，因此，研究城市物流无人机起降点布局规划方法具有现实意义。

目前，国内外无人机起降点布局规划研究较少。SHAVARANI等[2]认为无人机物流是缓解地面交通拥堵的重要途径，建立以总成本最小为目标的选址模型，并以旧金山为场景开展验证；钱欣悦等[3]引入了空域环境限制条件，建立末端起降点选址分配模型；VENKATESH 等[4]采用混合整数规划方法分别优化验证有容量和无容量限制的机场选址；DASKILEWICZ 等[5]面向城区居民通勤需求，考虑区域人口分布因素，探讨城市起降场分配问题，并以实际场景进行验证；HONG 等[6]为扩大无人机飞行覆盖范围，提出建立无人机充电设施优化选址模型，以菲尼克斯为例，采用混合整数规划和启发式算法求解；陈刚等[7]针对配送中心不同类型和需求点的不同需求，建立了以总里程最小为目标的无人机配送中心选址模型。纵观已有研究成果，部分研究考虑单一影响因素，忽视实际禁飞区限制，忽视实际物流配送中的容需匹配问题；少数研究虽提出充电桩等设施概念，但未明确划分起降点规模和等级，易造成供给侧资源短缺，影响服务质量。

本文面向城市区域的末端物流配送需求，从经济和效率的角度出发，考虑禁飞区限制、无人机性能条件、容需匹配等约束，建立城市物流无人机起降点布局规划模型，设计人类学习优化算法进行求解，确定满足需求的最佳起降点布局规划。

1 模型构建

1.1 问题描述及相关假设

本文城市物流无人机起降点布局规划面向高密度、短运距、高重复性、分布较为不均的城市末端物流配送需求，旨在完成对城市区域内具有物流集散属性的起降点布局规划，实现末端物流配送需求的精准覆盖。已知城市区域末端物流需求分布，包括所有需求点的坐标及具体需求量，需求量即所需配送业务量(单位：单)，现以垂直起降旋翼无人机为运输载具，执行“点对点”物流配送，完成配送任务后直接返回原起降点，不考虑无人机中转问题；为保证城市区域内所有物流需求得到满足，需考虑城区末端物流需求特征，对城区内物流无人机起降点进行布局规划。

为简化计算过程，本文作以下假设：

(1)物流无人机仅执行直线“点对点”的物流配送任务且每次仅能配送一单，且货物的体积、重量等属性不超出物流无人机性能限制。

(2)不考虑物流配送过程中的无人机冲突问题及延误问题。

(3)所有备选点均具备垂直起降能力的无人机及其配套保障设施。

(4)考虑到城市区域末端物流需求量分布不均，为合理布局规划，将物流无人机起降点等级划分为3 级，其规模由大到小依次为1 级、2 级、3 级，分别承担大规模物流需求区域、中等规模物流需求区域、小规模物流需求区域的物流配送任务。相应地，无人机起降点的成本投入、容量、服务范围有所区分。

1.2 多目标规划模型

1.2.1 模型重要符号说明

表1为模型重要参数及符号说明。

表1 符号说明Table 1 Notation summary

1.2.2 目标函数

(1)经济成本函数

以经济成本C最小为优化目标，即

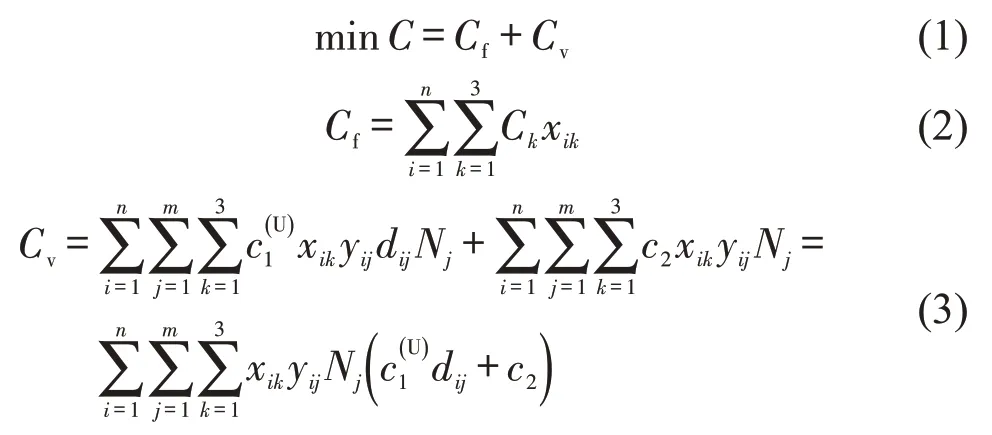
式中：Cf为固定成本，指单位时间内起降场点运行投入的必要固定成本，主要包括场地租赁或使用费用等；Cv为变动成本，指单位时间内起降点运营所投入的变动成本。

(2)客户满意度函数

本文参考了客户时间满意度思想，以总客户满意度最高为优化目标，即

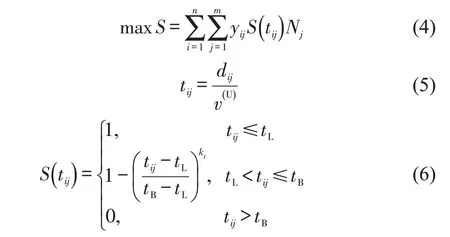
式中：S为总客户满意度，本文采用凹凸时间满意度函数计算客户时间满意度；kt为客户时间敏感系数。客户时间满意度变化曲线如图1所示。

图1 时间满意度曲线Fig.1 Time satisfaction curve

1.2.3 约束条件

(1)起降点数量约束

起降点布局总数不能超过备选起降场址的数量，即

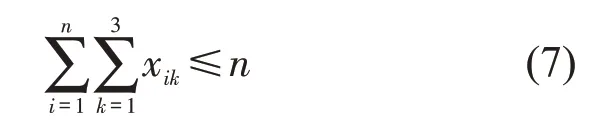
对于任意备选起降点i，不允许设置多个级别的起降点，即

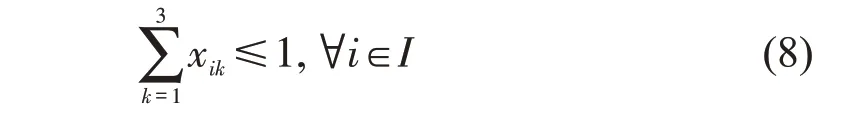
(2)供需点匹配约束

对于任意需求点j，有且仅有1 个起降点负责配送，不允许存在需求点不被配送或多供给点配送的情况，即

(3)容需匹配约束

对于任意备选起降点i，若i被选中，其容量必须满足需求量(配送业务量)，即

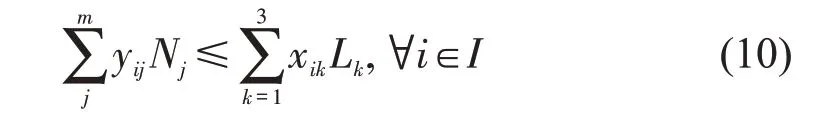
(4)禁飞区约束

对于任意备选起降点i与需求点j，若两点之间直线飞行路径跨越禁飞区，则配送关系不成立，即

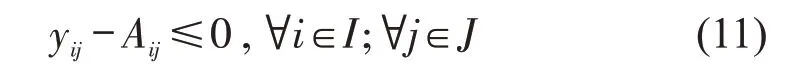
(5)起降点服务范围约束

起降点仅能配送以起降点为圆心，半径为Rk的服务范围内的需求点，即

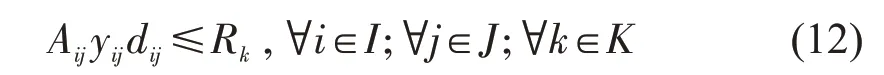
(6)物流无人机性能约束

物流无人机实际航程不得超过其最大航程，即

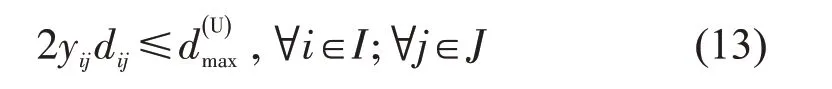
(7)配送关系约束

当点i被选为起降点时，起降点i与需求点j之间可能存在配送关系，即

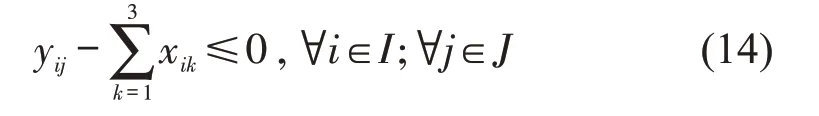
(8)变量取值范围

2 算法设计

本文通过设计人类学习优化算法(HLO)求解，计算得到基于需求分布的物流无人机起降点布局。

2.1 编码方式

初始种群编码方式为

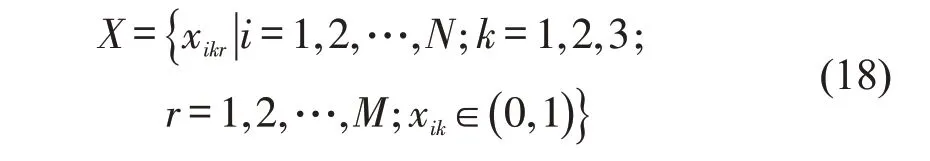
式中：N为解的维数；M为群体规模。个体编码方式示意如图2所示。已知起降点布局，根据最短路径配送原则，配送关系随之确定。

2.2 设置适应度函数

2.2.1 目标函数处理

本文所建立的布局规划模型包含最大化目标与最小化目标，为求解模型总目标函数值，对目标函数作归一化处理，即

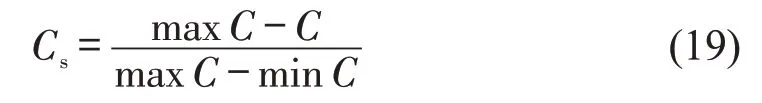
式中：成本C为逆向目标，值越小越优；maxC为所有备选起降点均建立1级起降点时的总成本，为经济总成本最大值；minC为不建设任何起降点的总成本，即为0，为经济总成本最小值；Cs∈[ 0,1)。

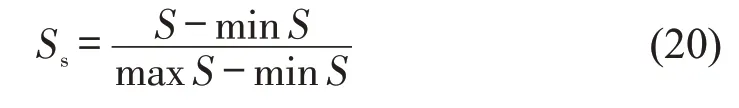
式中：满意度S为正向目标，值越大越优；maxS为每单快递的时间满意度均达到1 时的总客户满意度，为总客户时间满意度最大值；minS为每单快递的时间满意度均为0时的总客户满意度，为总客户时间满意度最小值；Ss∈[0 ,1]。

综上，模型的总目标函数设为

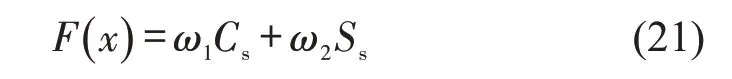
式中：ω1、ω2分别为Cs和Ss的权重，F(x)∈[ 0,1)。

2.2.2 约束条件处理

在求得F(x)基础上，执行约束条件判断，若存在任意约束不满足，适应度函数G(x)=0；若所有约束均满足，则G(x)=F(x)。

禁飞区变量Aij难以被直接计算，需进行处理，Aij计算方法如图3所示。

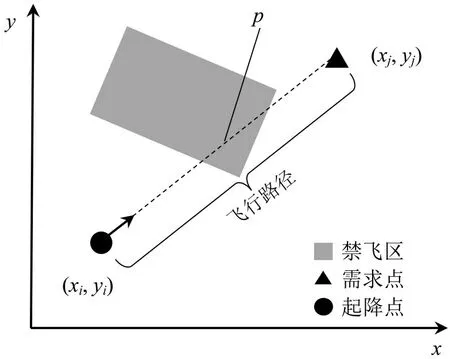
图3 跨禁飞区判断示意图Fig.3 Schematic diagram of cross no-fly zone judgment

Step 1 输入起降点坐标(xi,yi)、需求点坐标(xj,yj)以及禁飞区边界坐标集合Z。

Step 3 设置采样步长f，计算采样点个数。

Step 4 计算需求点与起降点之间的采样点集合R为

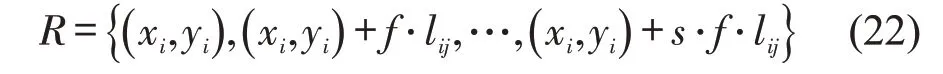
Step 5 利用MATLAB inpolygon 函数判断点p∈R是否落在禁飞区内，若存在采样点位于禁飞区内，Aij=0；否则，Aij=1。

Step 6 输出Aij。若Aij=0，则令dij=+∞；若Aij=1，则dij保持不变。

2.3 算法学习机制

人类学习优化算法作为新型智能群优化算法，由WANG等[8]于2014年首次提出，引入3种学习算子：随机学习算子、个体学习算子、社会学习算子，通过不断学习迭代生成新的解决方案。

(1)随机学习

人类学习过程包含一定的随机性，人类通常会通过随机学习探索新领域，人类随机学习行为是整个种群进步的保证。因此，设计随机学习算子为

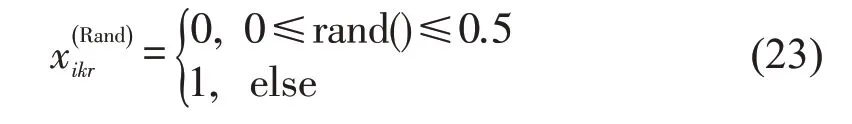
式中：rand()为在0和1区间内取随机数。

(2)个体学习

人类学习过程中通常会积累经验，构建个人知识库，依靠自身学习经验和先验知识避开错误答案。因此，设计个体学习算子为

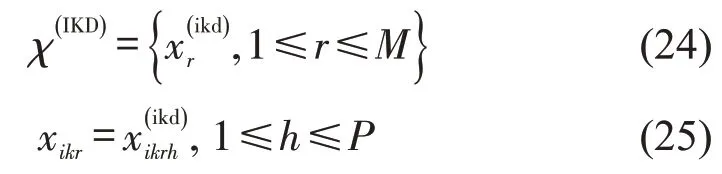
(3)社会学习

除了随机学习和个体学习外，人类会从社会集体中汲取经验，达到快速充实个人知识的目的。因此，设计社会学习算子为

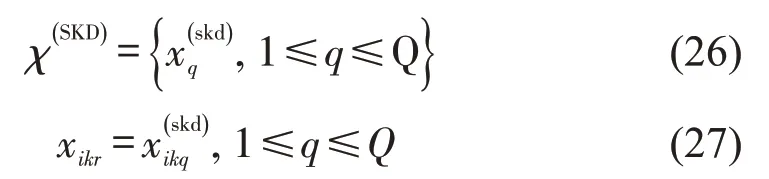
(4)人类学习操作

依概率执行人类学习操作，不断迭代产生新一代种群，即

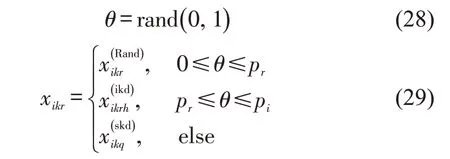
式中：θ为[0,1]区间的随机数；pr为随机学习概率；pi-pr为个体学习概率；1-pi为社会学习概率。算法流程设计如图4所示。

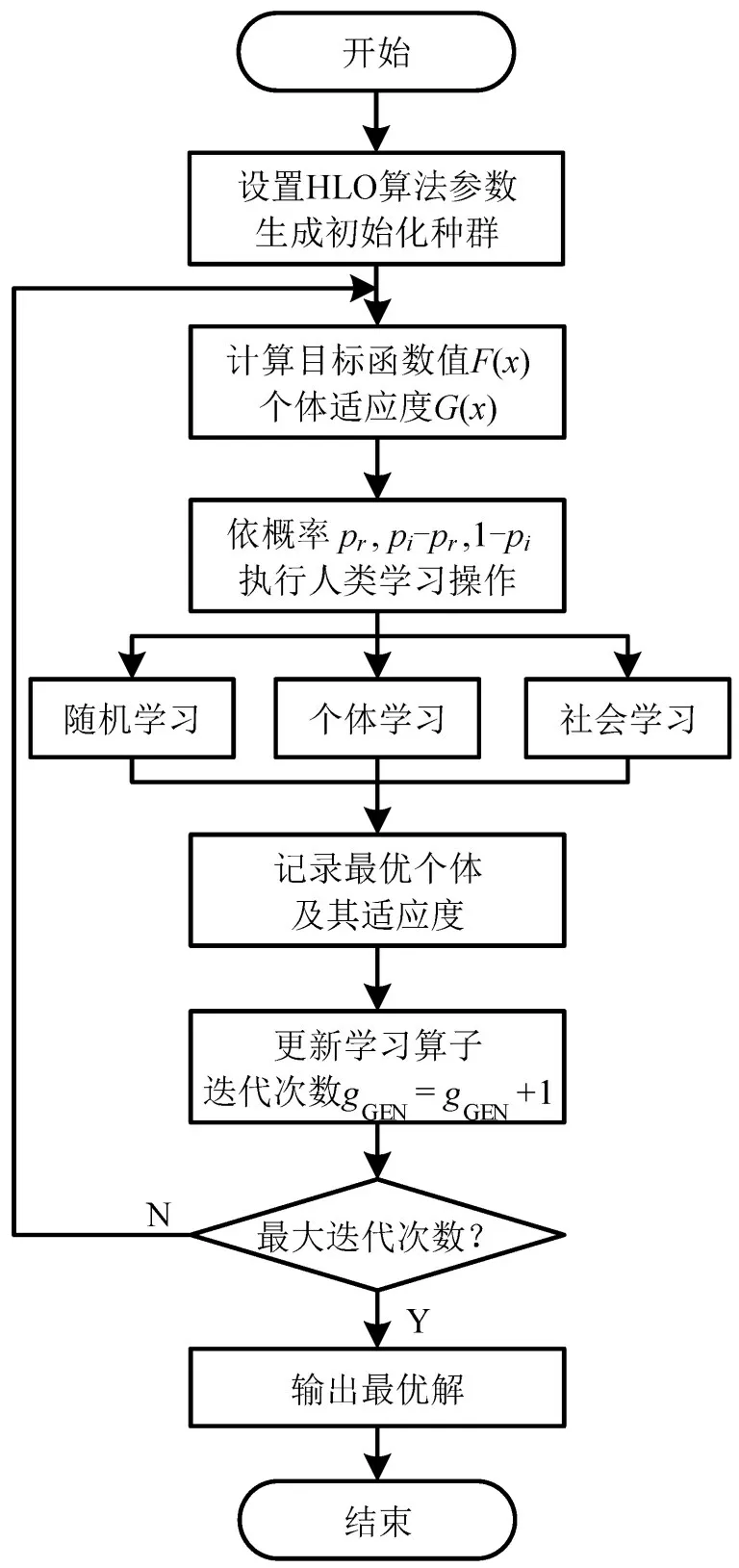
图4 算法流程Fig.4 Algorithm flow

3 算例验证

3.1 仿真环境与参数设置

为验证模型与算法有效性，使用MATLAB 进行仿真实验。引用文献[9]上海市某物流需求分布数据，如表2所示，物流需求量400单以内需求点占比约为74.26%。仿真环境如图5所示，包含上海虹桥机场禁飞区与分布在禁飞区外的202 个物流需求点，圆点大小反映了需求量。

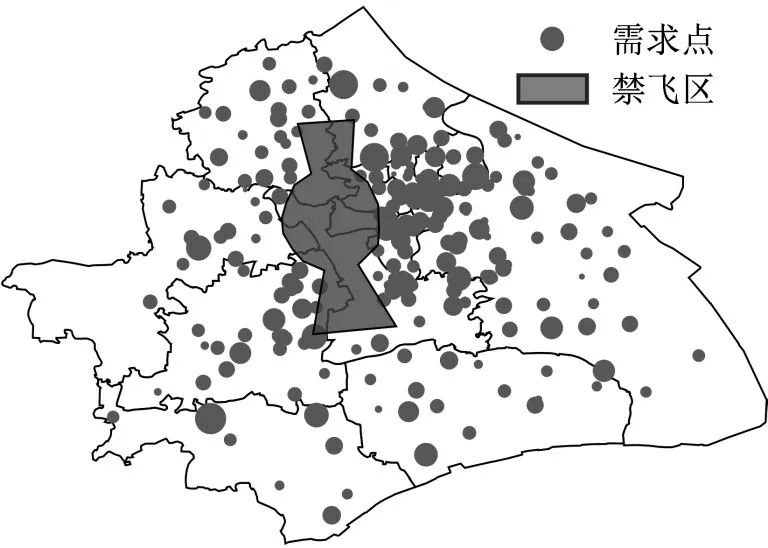
图5 仿真环境示意图Fig.5 Schematic diagram of simulation environment

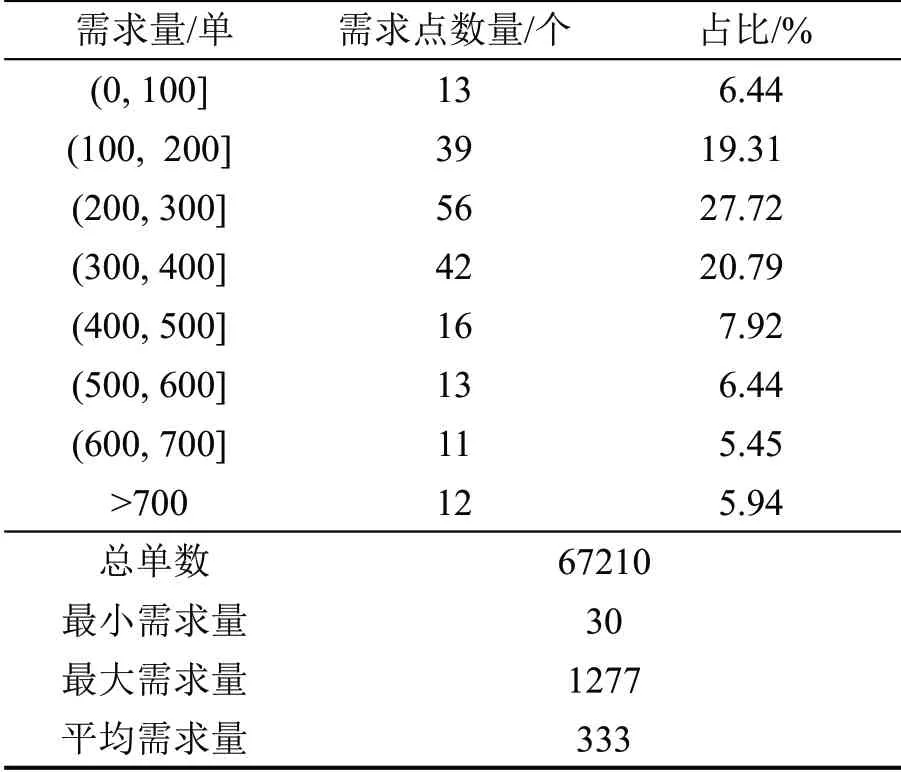
表2 上海市某物流公司物流需求量分布Table 2 Distribution of logistics demand of a logistics company in Shanghai

由图5 可见，在仿真环境内，物流需求点不均匀地分布在城市各个区域；同时，各需求点的需求量存在较大差异，城中心区域物流需求点密集且需求量较大。由于缺乏实际备选起降点相关数据，假设所有物流需求点均可作为备选起降点。

基于前期研究和需求数据分析，综合考虑文献[2,3,7]参数设计，结合亿航、顺丰、大疆等物流无人机机型技术性能参数，设置模型参数，如表3所示，本参数设置仅用于仿真，后续应用需结合实际情况酌情设计。

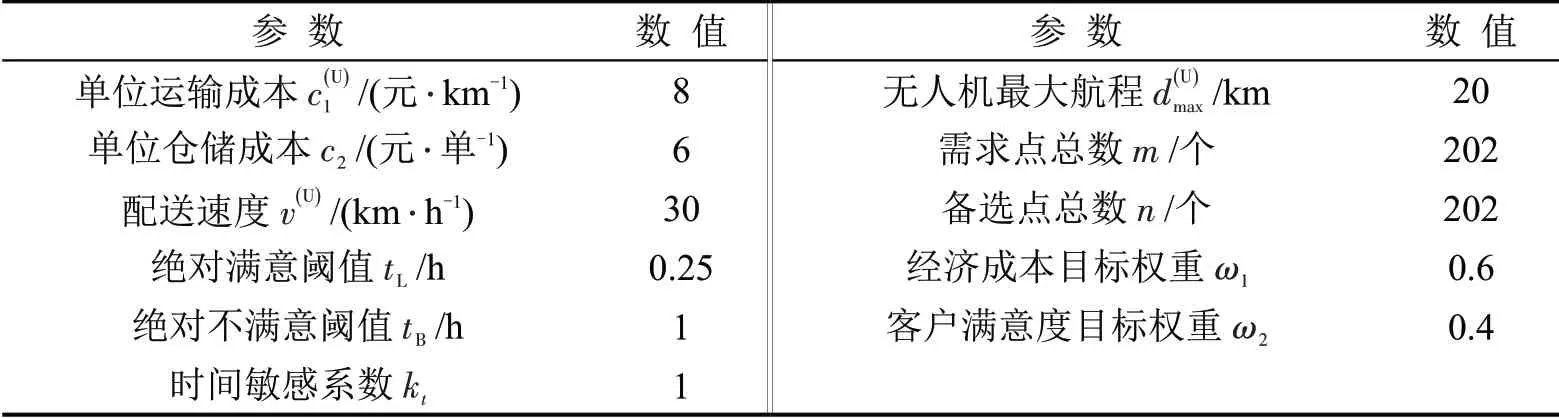
表3 模型参数设置Table 3 Model parameter setting

基于需求数据处理、结果分析，各级起降点具体参数设置如表4所示。

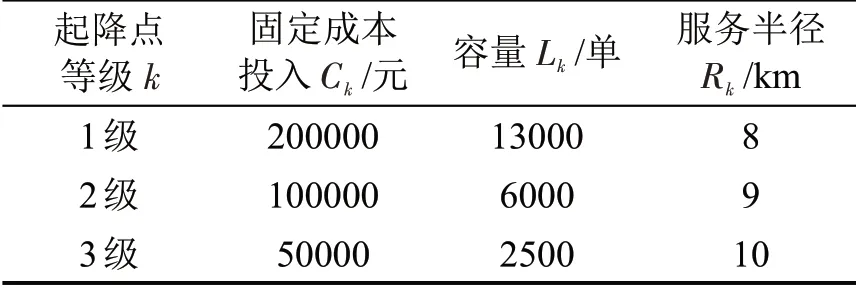
表4 起降点参数设置Table 4 Parameter setting of vertiports

3.2 结果分析

基于上述仿真环境与参数设置，通过人类学习优化算法求解模型，重复实验30组，平均成本消耗为4779603 元，平均满意度为0.9933。选取1 组较优解展示，起降点布局规划结果如表5所示。包含1个1级起降点，9个2级起降点以及11个3级起降点共21个起降点，实现了需求的全覆盖，所有起降点容量均能满足其覆盖需求点的需求量，即总供给量小于容量。基于该布局规划方案，经济成本消耗约为4664584 元，平均客户满意度为0.9950，结果良好。

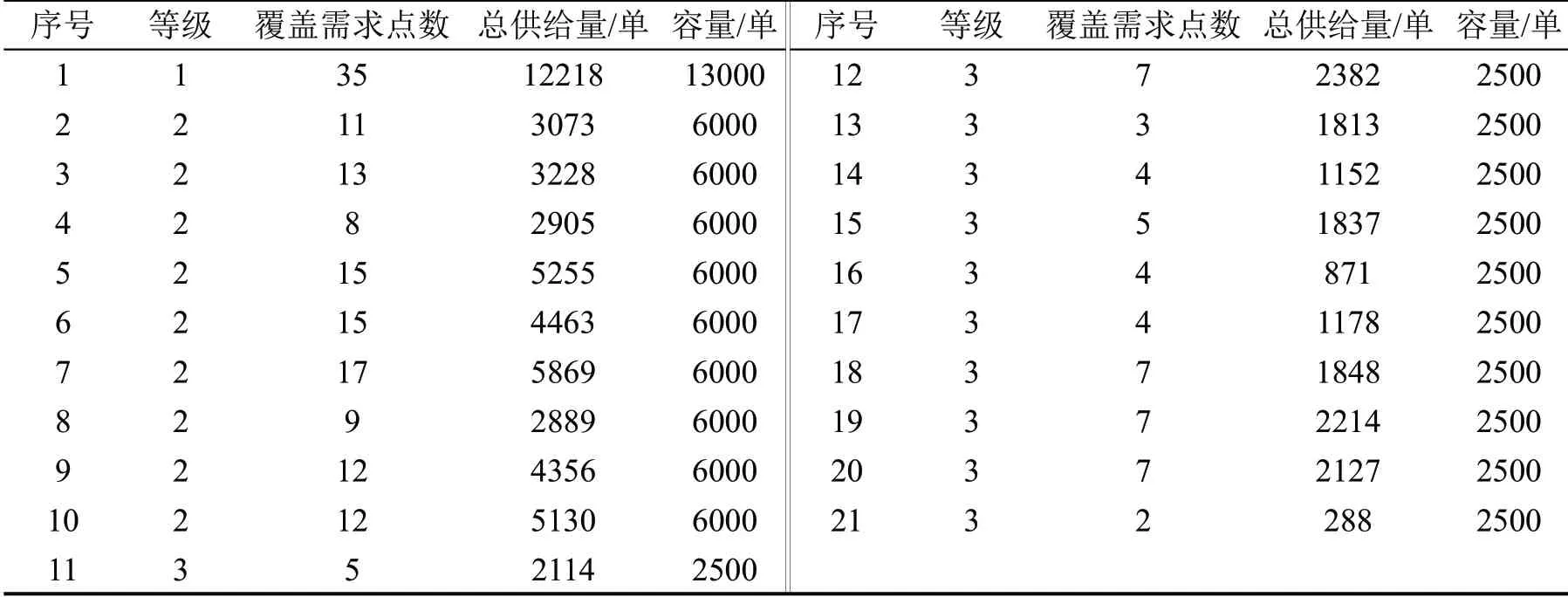
表5 起降点布局规划结果Table 5 Layout planning result of vertiports

基于当前解的起降点布局如图6所示。

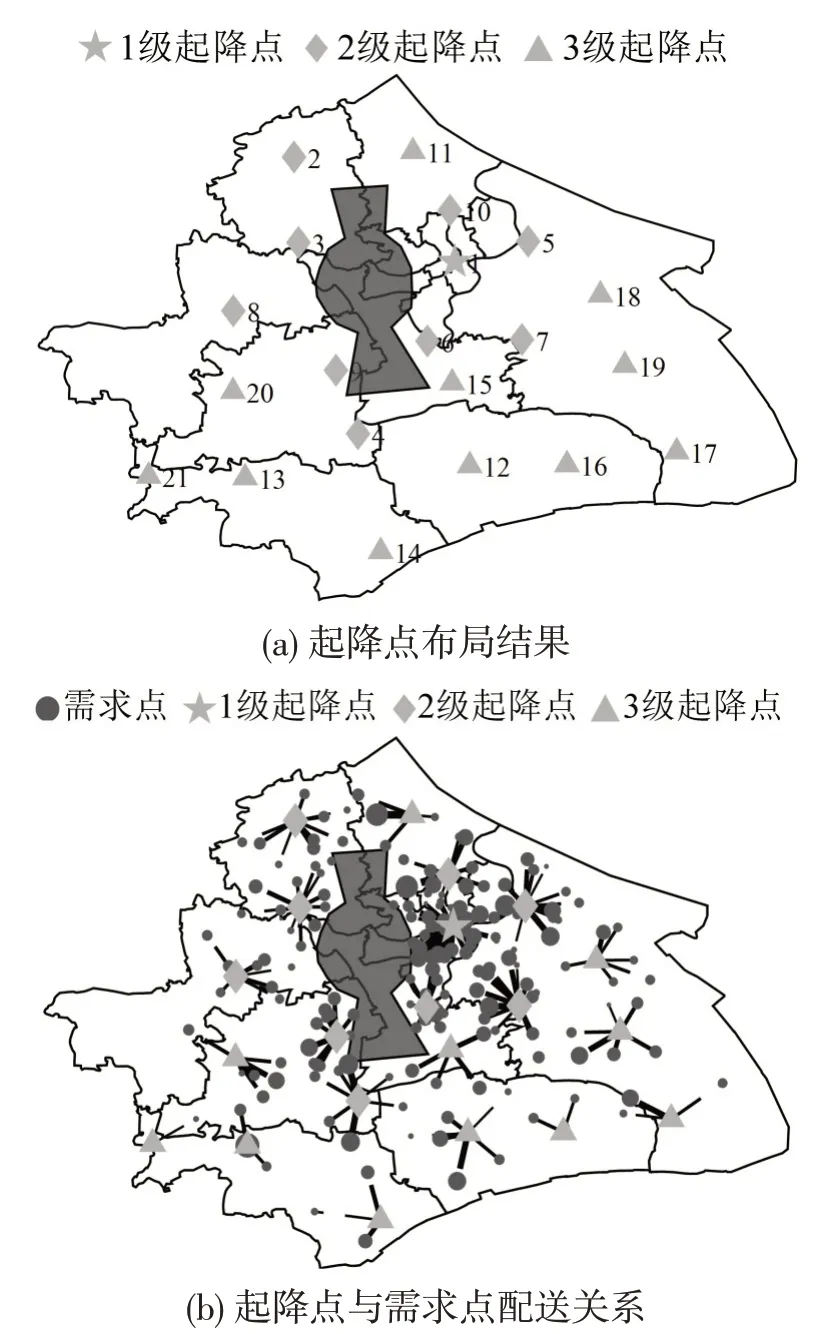
图6 城市物流无人机起降点布局Fig.6 Layout result of urban logistics UAV vertiports

由图6可知，起降点较为均匀地分布在各个区域，由虚线将起降点和需求点相连接表示具体配送关系。其中，1 级起降点主要分布在城市中心繁华区域；2级起降点分布相对偏远；3级起降点主要分布在城郊，用于弥补1级和2级起降点的覆盖空白，符合实际。

为分析算法性能，采用遗传算法求解，2种算法迭代效果对比如图7所示，相较于遗传算法，人类学习优化算法表现出更快的收敛速度并求得更高适应度值，优势显著。

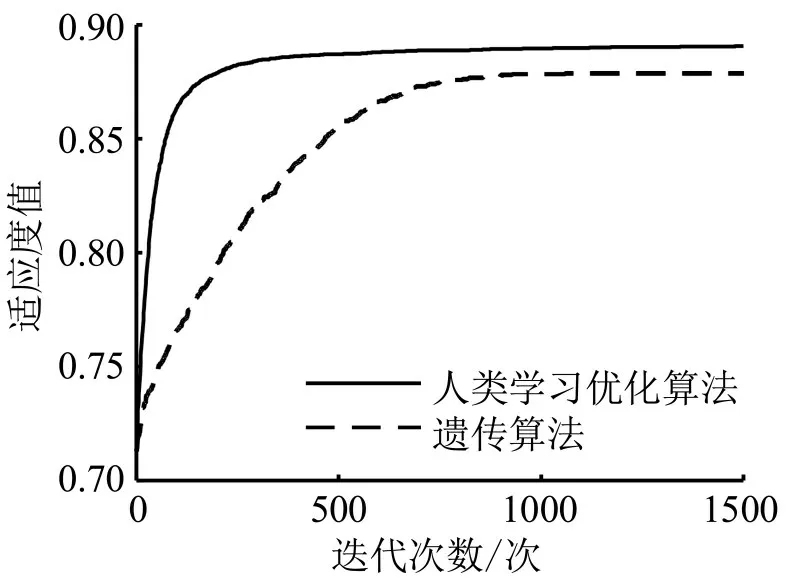
图7 迭代效果对比示意图Fig.7 Schematic diagram of iteration effect comparison

3.3 参数设置分析

目标权重{ω1,ω2} 与算法学习概率参数{pr,pi}取值对实验结果和收敛速度存在影响，因此，设计以下对照实验。

3.3.1 目标权重

起降点布局需在满足约束的前提下，尽可能缩减成本，增加满意度，为分析目标函数权重{ω1,ω2}对结果的影响，进行11组对照实验，目标函数值随权重变化如图8所示。

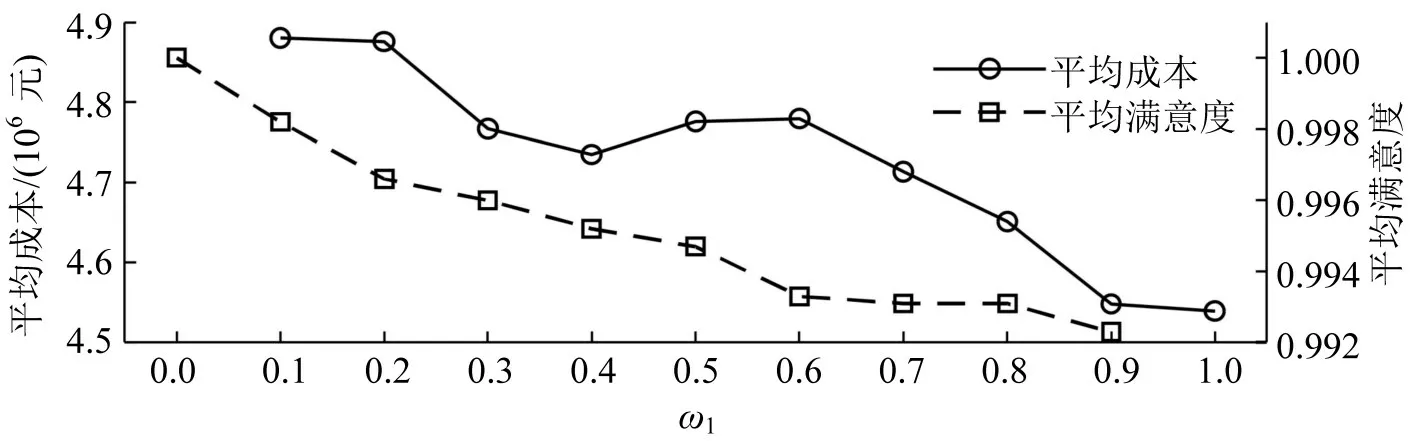
图8 目标函数值随权重变化曲线Fig.8 Change curve of objective function values with weights

由图8可知，随着成本目标权重ω1的减小与满意度目标权重ω2的增大，平均成本呈递增趋势但有所波动，同时平均满意度逐渐增大；基于构建模型的目标函数值，实验7 表现出最佳布局结果，最佳权重取值为：ω1=0.4，ω2=0.6。

3.3.2 算法学习概率参数

为分析学习概率参数{pr,pi} 对结果影响，设计9组对照实验，结果如表6所示。当pr保持不变，随着pi的增大，成本呈上升趋势，同时，满意度略有降低；当pi保持不变，pr=5/n效果较优。最优算法学习概率参数设置为pr=5/n,pi=0.80+2/n。

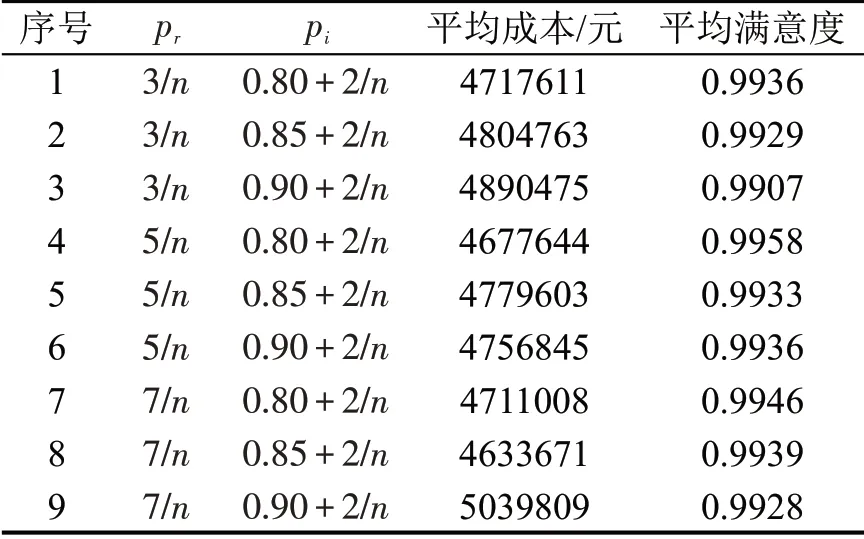
表6 算法参数对布局规划结果影响Table 6 Influence of algorithm parameters on layout planning results

4 结论

本文在考虑无人机性能约束和禁飞区约束的基础上，针对城市物流无人机起降点布局规划问题，综合考虑起降点建设经济成本和客户满意度，构建3级布局规划模型，设计人类学习优化算法进行求解。基于上海市某物流公司物流量数据和上海市地理信息数据，构建包含禁飞区和202个需求点的仿真环境进行实验。结果表明，所建模型与算法可以被用于起降点布局规划问题，针对不同需求密度片区，起降点建设等级区别明显；同时，人类学习优化算法相较于遗传算法表现更佳。本模型可用于城市物流无人机起降点布局规划，规划结果、收敛效果等受参数取值影响，在其他场景和需求下，可参考本文参数设计。

随着我国低空空域改革的推进，物流无人机相关技术的成熟，物流无人机相关配送体系的构建为期不远，由于起降点布局规划问题相关研究的实际需要，今后研究将考虑多种机型、多种配送方式，例如，空地联运等研究。