基于混合整数非线性规划的接驳公交优化模型

宋俪婧，白同舟，贺玉龙，陈艳艳，刘雪杰，马腾腾

(1.北京工业大学，北京市交通工程重点实验室，北京100124；2.北京交通发展研究院，北京 100073)

0 引言

随着我国城市轨道交通的不断建设成网，轨道交通与地面公交的协同发展已成为大城市公共交通优先发展的重要研究课题之一，因此，接驳公交线路的设计与运营方案的优化具有非常重要的意义。接驳公交线路设计与运营方案优化通常涉及线路设计、发车频率优化及时刻表编制等关键问题。

现有关于接驳公交的研究主要集中在接驳公交线路设计和运营优化两个方面。在接驳公交线路设计方面，文献[1]以最大化路径需求潜力为目标建立目标函数，兼顾路径旅行时间和圈点线路约束建立求解圈点线路的数学模型，设计路段交叉变异算法，实现模型的启发式求解。文献[2]考虑公交站点与城市轨道交通车站间的弹性客流需求，分析乘客出行选择行为与接驳公交线网规划的博弈关系，构建以管理者、出行者及社会运营成本的总费用最小为目标的接驳公交线路优化模型，采用遗传算法求解。文献[3]以出行时间和可达性为目标建立模型，分析公交乘客不同需求下的接驳公交线路设计方案。文献[4]提出接驳高铁车站的公交线路设计方法，提出接驳公交线路设计模型并设计算法求解，与城市轨道交通站点研究方法类似。在接驳线路运营方面，文献[5]以车辆满载率为约束条件，以等待时间、换乘时间及车上时间等综合成本最小为目标函数，提出为BRT走廊干线接驳的线路发车频率优化的非线性模型。文献[6]构建接驳公交运营的多目标优化模型，设计了利用产生式方法获得Pareto 解集的遗传-变邻域搜索算法，通过算例验证了模型与算法的有效性。文献[7]综合考虑乘客出行行为和出行意愿，建立了接驳公交时刻表优化模型。文献[8]以乘客出行时间延误最小为目标，以车辆容量和车队规模为约束条件，构建接驳公交时刻表优化模型，并应用遗传算法和基于Frank-Wolfe 算法并结合发车时间调整的求解算法(FWSDT)求解模型，通过实例验证模型的准确性和有效性。文献[9]以等待时间最小为目标函数，以车辆数量和车头时距为约束条件，应用启发式算法优化发车频率。上述研究中为了降低模型复杂程度，提升运算速度，大多将接驳公交网络设计与发车频率优化作为相互独立的步骤进行研究，而对于接驳公交网络设计和发车频率协同优化的研究较少，仅有文献[10]建立以乘客数最大和出行时间和运营成本最小为目标的同步协调模型，采用基于非支配排序的遗传算法求解模型。但仅假定乘客由候选接驳公交站点到达给定的1个城市轨道交通车站，客流模式为“多对一(M to 1)”。现状研究中，对于“多对多(M to M)”的研究较少，模型与实际情况的接近程度有待提升。在模型规划方法方面，主要采用多目标模型和双层规划模型等方式，线性规划模型较多。

基于上述问题，本文改进了以往优化模型将接驳公交网络设计与发车频率单独进行优化的模式，将接驳公交网络设计和运营协同综合优化；突破了以往优化模型大多考虑单一目的地(M to 1)的模式，提出的优化模型将扩展到接驳服务区域内任意轨道站点和公交接驳需求点之间的多对多(M to M)分布，优化模型更加符合现实需求分配。

1 问题描述与建模

本文基于接驳公交优化中公交网络设计和发车频率优化两个关键问题，建立接驳公交网络设计与发车频率协同优化模型。基于大城市轨道交通和地面公交功能定位、线网结构与运营标准等实际情况，综合考虑选取决策变量，构建优化目标函数和约束条件，并依据目标函数和约束条件的特点，采用混合整数非线性规划模型。同时，为更贴近接驳区域实际客流特征，将需求模式扩展为“多对多”，即每个候选接驳公交站点到研究区域内多个城市轨道交通车站均存在OD关系。

1.1 问题描述

城市轨道交通接驳公交线路具有以下特点：1条接驳公交线路服务多个需求点，例如，居住区、工作地、学校、医院及交通枢纽等主要客流吸引点；接驳公交线路由多个备选站点组成线路候选站点集，需要依据乘客出行需求从中选择若干作为接驳公交站点；选取的公交站点中最接近轨道交通站点的为换乘车站，乘客可在该换乘车站完成轨道交通与接驳公交线路的换乘，在服务区域内，多个接驳公交站点可服务多个轨道交通站点。

乘客乘坐轨道交通换乘接驳公交线路实现门到门出行，换乘时间和接驳公交的在途时间以及公交发车时刻如何与轨道交通到站时间有效衔接，是提升整个出行链出行吸引力的两个关键因素。同时，接驳公交线路运营成本也是激发运营企业提升服务的关键因素，因此，需要在综合考虑乘客出行时间和运营成本的条件下，将公交网络设计与发车频率协同优化。变量和集合定义如表1所示。

表1 变量和集合定义Table 1 Variable and collection definition

1.2 模型构建

本文选取接驳公交乘客总出行时间最小化和运营成本最小化为优化目标，构建接驳公交线路发车频率协同优化模型。以接驳公交线路发车时刻、各条接驳公交线路长度及接驳公交发车频率作为决策变量，约束函数包括：接驳线路完整性约束、“多对多”模式约束、接驳线路车辆承载能力、可使用车辆数、服务时间、发车时刻、接驳线路长度、发车频率及0-1决策变量约束。决策变量包含0-1决策变量和连续变量，因目标函数是非线性的，故所建立的优化模型属于混合整数非线性规划问题。

(1)乘客出行时间成本

乘客总出行时间Z1，包括公交需求点处车辆停顿接客时间，各公交需求点间的行程时间及轨道与接驳公交的换乘时间，即

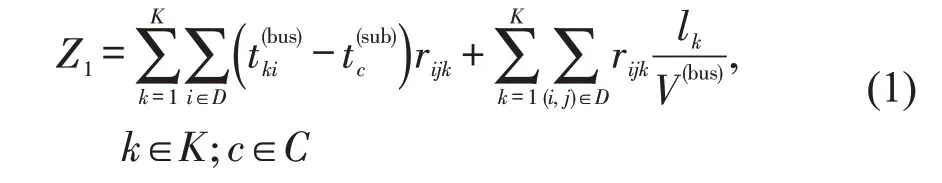
式中：i,j为路段节点编号；lk为连续变量，接驳线路k在节点i,j之间的弧段(i,j)的路径长度，根据节点i和节点j的经纬度坐标，依据三角推导计算两点间距离，获得弧段(i,j)的路径长度。当节点i,j之间存在多条弧段的时候，搜索两点之间的最短路。具体方法为，依据路径长度形成各顶点间的邻接矩阵，分别建立最短路集合和未确定最短路的点集合。从起点开始搜索，按最短路径长度的递增次序依次把第2 组的顶点加入到最短路集合中。在加入的过程中，总保持从起点到最短路集合中各顶点的最短路径长度不大于从起点到未确定最短路集合中任何顶点的最短路径长度，通过搜索计算后的起点至最短路集合中的路径即为弧段(i,j)之间的路径，其长度即为弧段(i,j)的路径长度，各弧段路径长度之和即为接驳线路k的长度lk。

(2)接驳公交线路运营成本

接驳公交线路运营成本Z2通过接驳公交总运营里程数乘以单位里程运营费用得到，即

(3)约束条件

①接驳公交线路完整性约束

路线完整性约束，即每条接驳公交线路应至少包括1个轨道站点和1个接驳公交站点，即

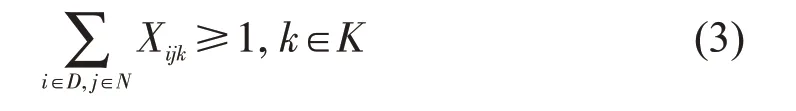
②“多对多(M to M)”模式约束

每条接驳公交线路从1个轨道站点出发，终点可返回另1个轨道站点，即

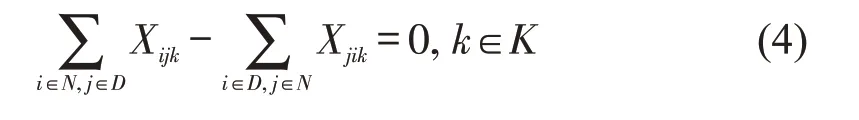
③接驳线路车辆承载能力约束

对于路线k，轨道交通换乘接驳公交的乘客数量不能超过接驳公交容量，即

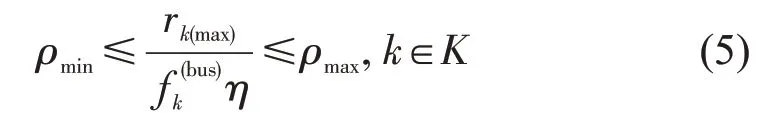
式中：rk(max)为接驳线路k最大断面客流量；η为接驳公交车辆核定载客；ρmin为最小满载率；ρmax为最大满载率。

④接驳线路可使用车辆数约束

线路发车频率受公交车辆在给定范围内的总行驶里程限制，即

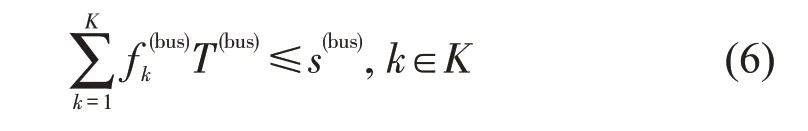
⑤接驳线路服务时间约束

对于线路k，服务时间需满足接驳服务需求，在一定的服务水平范围内，即

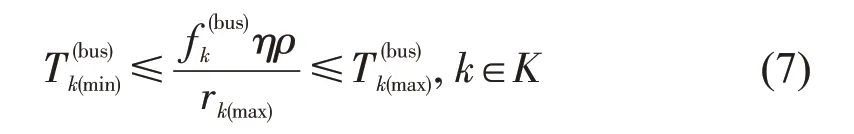
⑥接驳线路发车时刻约束

接驳线路k在需求点i的发车时刻应满足当接驳公交线路k经过弧段(i,j)时，对应的需求点i的发车时刻才不为0，即

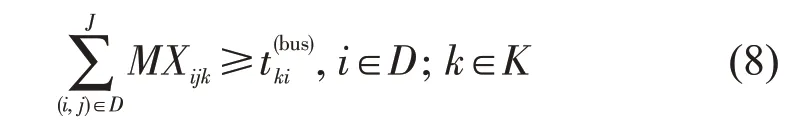
式中：M为很大的正数。

⑦0-1决策变量约束

模型中涉及的0-1决策变量需满足

⑧接驳线路长度约束

接驳线路k的长度应满足接驳公交实际运行情况，即

⑨接驳公交发车频率约束

接驳线路k的发车频率应满足接驳公交实际运行情况，即

1.3 协同优化模型

考虑乘客和运营商的利益，最大限度地减少乘客的综合旅行成本和运营商成本，接驳公交线路和运营协调优化模型为最小化Z1和Z2，即

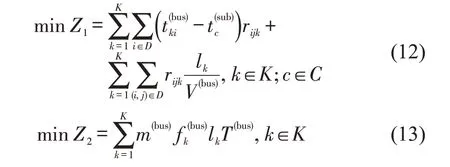
目标函数式(12)和式(13)与约束条件式(3)～式(11)构成了接驳公交协同优化模型，优化模型具有以下特点：将接驳公交线路和运营协同优化；最优目标是最小化乘客出行成本和接驳线路运营成本，兼顾乘客和公交运营企业多方需求；乘客需求不限于单一目的地(M to 1)，扩展到接驳服务区域内任意轨道站点和公交接驳需求点之间的分布(M to M)，符合现实需求分配。

2 求解算法

本文建立的协调优化模型中具有连续变量和0-1决策变量，还有非线性函数，属于混合整数非线性规划模型，因此，直接求解原模型是非常困难的。为了使模型易于求解，需要对模型进行线性化处理，将非线性函数转化成线性函数形式，将模型重构为等价的线性模型，再通过线性加权组合法将双目标函数转化为单目标函数求解。

2.1 模型重构

在目标函数Z2中，涉及两个变量乘积的非线性形式，引入变量y，即

将式(15)分段线性化，即

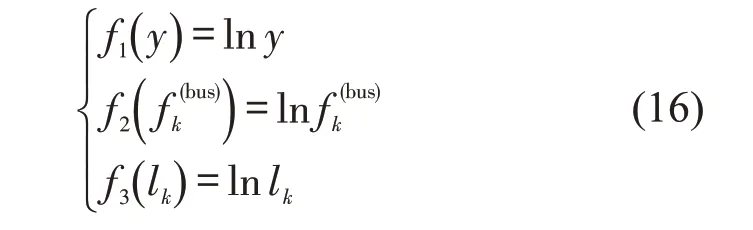
则原函数Z2中非线性形式被线性化为

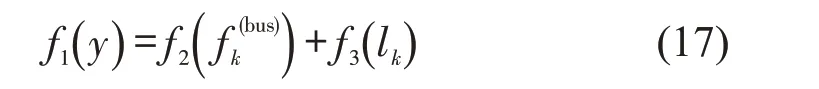
同理，约束条件按照上述方法处理。

依据上述方法，本文模型目标Z2可重构为

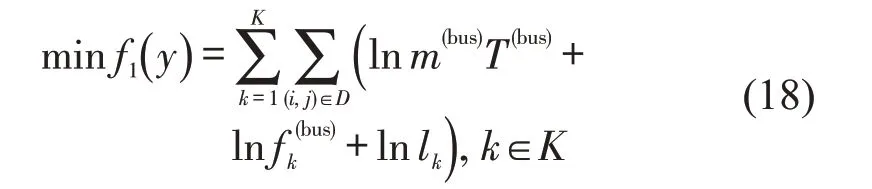
2.2 双目标函数的转化

在优化模型重构为线性模型后，为便于求解，将模型中的双目标函数转化为单目标函数，分为两个步骤。

Step 1 通过增加乘客平均出行成本F，将目标函数Z1转化为乘客出行成本(元)，与目标函数Z2的运营成本(元)量纲统一，转化后的目标函数Z1为

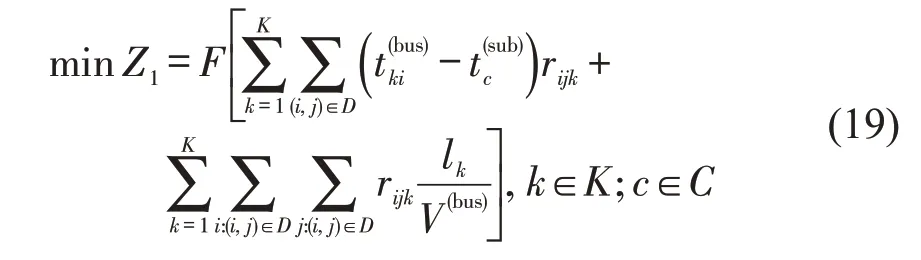
Step 2 应用线性加权组合法，即根据优化目标各影响因素的重要程度，分别赋予目标函数Z1和Z2相应的权重，将双目标函数转换为单目标函数。本文认为接驳线路主要服务乘客出行，因此，将考虑乘客出行成本的目标函数Z1的权重取值为0.6，将接驳线路运营成本权重取值为0.4。转化后的目标函数为

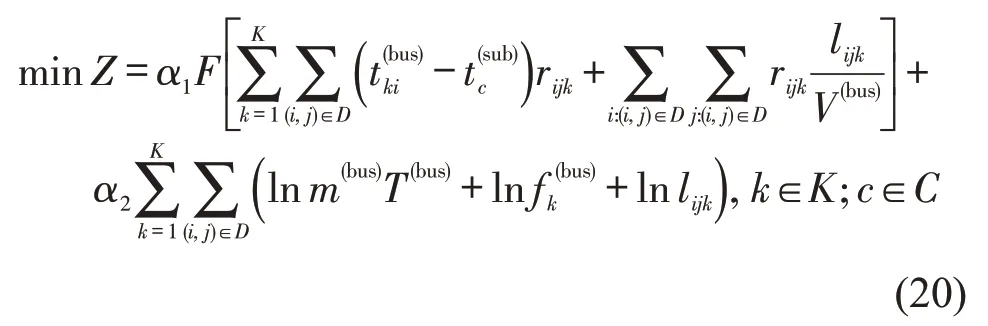
式中：α1为目标函数Z1的权重；α2为目标函数Z2的权重。

3 实例分析

3.1 实例说明及数据来源

本文以北京轨道交通7 号线垡头站和焦化厂站为研究实例分析验证模型的有效性。有轨道站点2 个(序号1 和序号2)，接驳公交需求点17 个(序号3～19)。轨道站点与公交需求站点拓扑关系如图1所示。接驳公交需求和轨道列车时刻表示例如表2 和表3所示，各需求点间路径长度如表4所示。

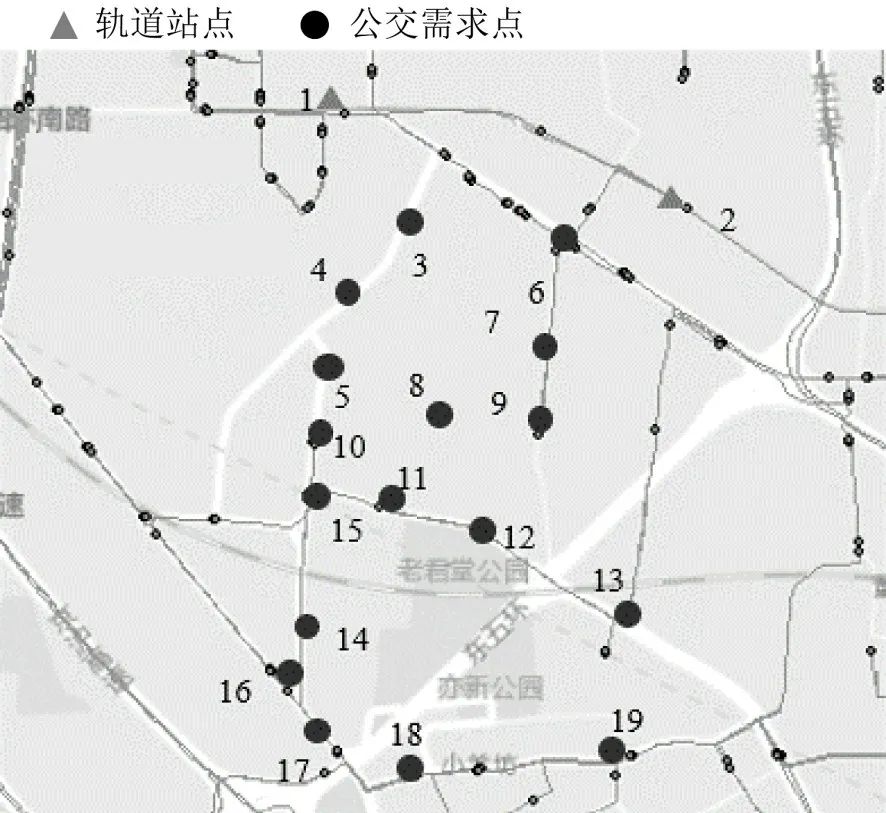
图1 7号线沿线轨道站点与公交需求站点拓扑关系Fig.1 Topological relationship between rail stations along line 7 and bus demand stations

表2 接驳公交需求示例（以部分需求点为例）Table 2 Example of feeder bus demand(人次·h-1)

表3 轨道列车时刻表示例（以垡头站为例）Table 3 Metro timetable example(Fatou station)

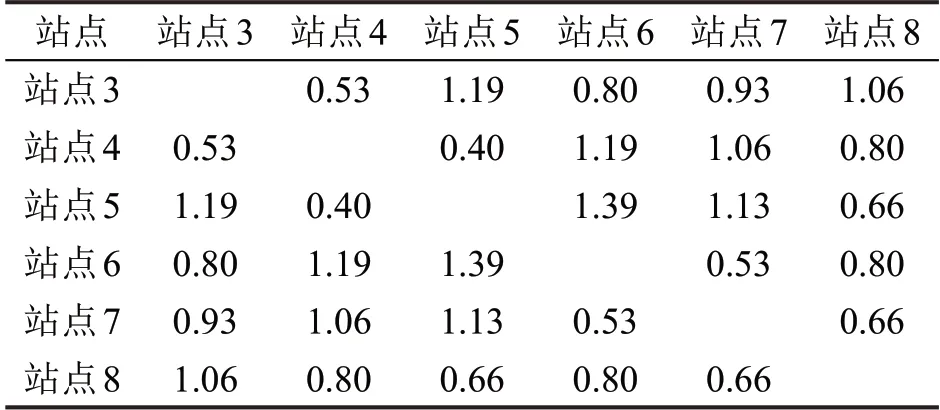
表4 各需求点间路径长度(以部分需求点为例)Table 4 Length between demand points(km)

3.2 实例结果与分析

依据本文建立的协同优化模型，获取各已知参数如下：接驳公交车辆平均运行速度15 km·h-1，接驳公交线路k每车次服务时间区间为10～20 min，接驳公交车辆额定载客40 人·车-1，接驳公交车辆满载率区间为40%～100%，接驳线路可用公交车辆10辆，接驳线路长度0～5 km，接驳线路发车频率2～60 车次·h-1，乘客平均出行成本1.5 元·人次-1。接驳公交在各弧段的客运需求通过出行需求预测并结合交通调查数据获得，轨道到站时刻通过官方发布的发车时刻表获得。

混合整数非线性规划模型重构后有35265 个约束条件，4278 个变量。调用数学规划求解器CPLEX求解模型，求解结果如图2所示。

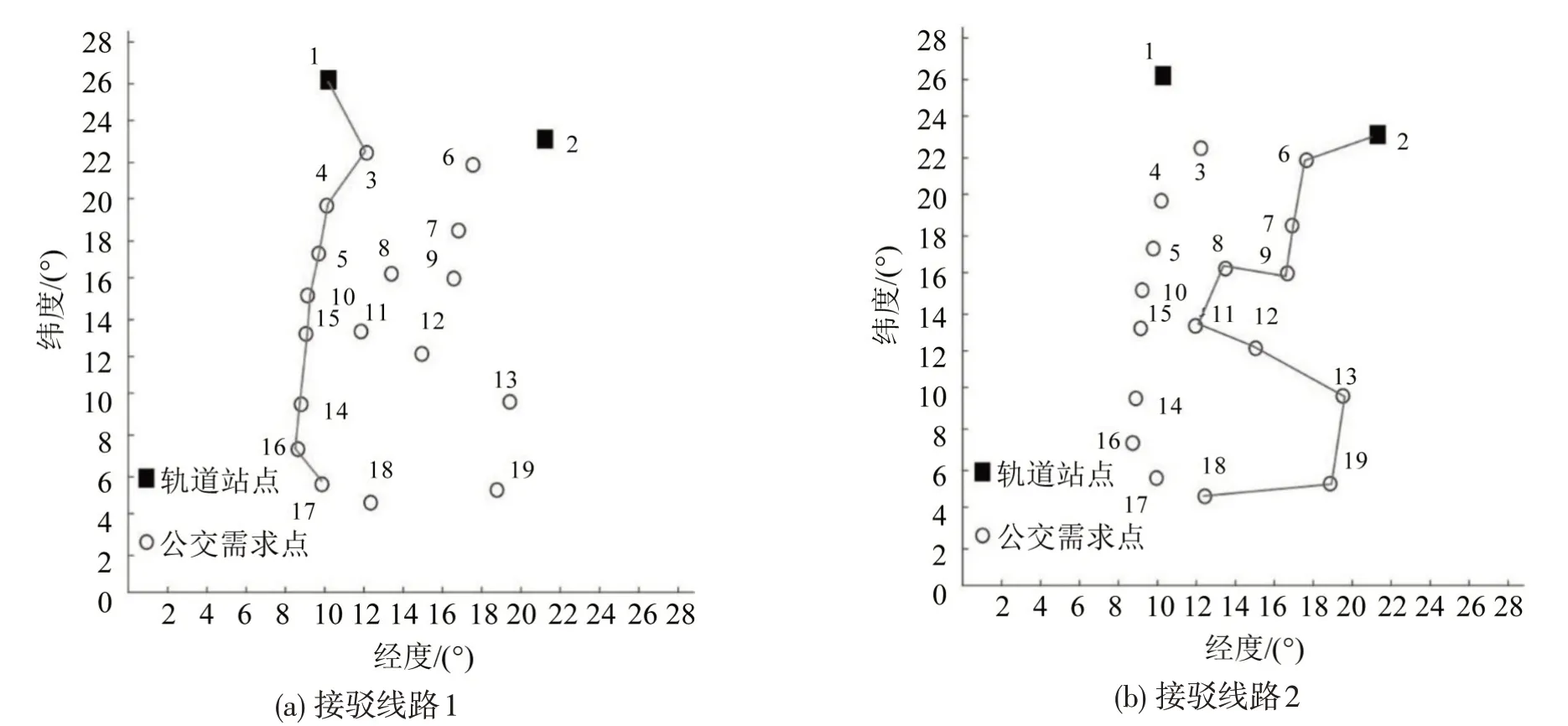
图2 模型求解结果Fig.2 Model results

根据图2求解结果绘制出接驳公交路线，最优接驳公交路线示例如表5所示。依据模型优化后的发车频率和接驳公交线路时刻表示例如表6所示。

表5 最优接驳公交线路Table 5 Optimal connection to feeder bus

表6 接驳公交线路1时刻表示例(垡头地铁站-小羊坊)Table 6 Timetable example of feeder bus route 1(Fatou-Xiao Yangfang)

从实例结果可以看出，本文所建立的协同优化模型能在满足线路完整性约束、接驳线路长度约束、多对多接驳模式约束、接驳线路发车频率及使用车辆数等约束条件下，得到满足乘客接驳需求的接驳公交线路路径和发车频率。

为证明协同优化模型所求解的可行性和准确性，在拓扑路网下应用深度优先搜索算法(DFS)[11]遍历轨道站点1的所有可行路径，生成路径302条，其中，287 条满足所有约束条件。对所有满足约束条件的路径计算其综合目标值和对应的发车频率值，选取最优综合目标值与优化模型结果进行对比分析，如表7所示。

表7 对比分析结果(以站点1为例)Table 7 Result of Comparative analysis

由表7可知，本文建立的优化模型综合目标值与DFS 算法所得值相等，且对应的最优路径相同。发车频率误差7%，符合微循环线路实际运营情况(发车频率在2～60 车次·h-1)。因此，可认为本文建立的协同优化模型可以得到最优的接驳公交线路路径和发车频率。

4 结论

通过本文分析，可以得到以下结论：

(1)既有研究关于接驳公交线路设计与运营方案优化通常涉及线路设计、发车频率优化及时刻表编制等关键问题，主要集中在接驳公交线路设计和运营优化两个方面。为了降低模型复杂程度，大多将接驳公交网络设计与发车频率优化作为相互独立的步骤进行研究。而将接驳公交线路设计与运营进行协同优化可以更全面地促进轨道交通与地面公交协同发展，且在模型构建方法和算法上是可行的。

(2)通过对以往研究的梳理分析，结合实际情况，发现乘客乘坐轨道交通换乘接驳公交线路实现门到门出行，换乘时间和接驳公交的在途时间以及公交发车时刻如何与轨道交通到站时间有效衔接，是提升整个出行链出行吸引力的两个关键因素，同时，接驳公交线路运营成本也是激发运营企业提升服务的关键因素。因此，在优化模型构建中可以选取乘客总出行时间最小和接驳公交线路运营成本最小作为模型目标函数，统筹考虑接驳公交线路设计与发车频率问题。

(3)以往研究在模型构建方面大多考虑多对一模式，即多条接驳公交线路对应1 个轨道交通站点，而在实际情况中，多条接驳公交线路可能对应多个轨道交通站点。因此，为更贴近接驳区域实际客流特征，可选取“多对多”模式作为模型约束条件之一，即每个候选接驳公交站点到研究区域内多个城市轨道交通车站均存在OD关系，使模型更接近实际情况。同时，结合相关规划和实际运营情况，接驳公交线路的完整性、长度、可使用线路条数及车辆数也是模型重要的约束条件。

(4)由于混合整数非线性规划模型中具有连续变量、0-1决策变量，同时，还有非线性函数，直接求解原模型是非常困难的。为使该模型易于求解，可通过0-1决策变量和非线性函数进行线性化处理等方式，将模型重构为等价的线性模型后再进行求解，可有效降低原模型复杂度。

(5)通过实例分析得到接驳线路和相应发车频率，与相同拓扑路网下应用深度优先搜索算法(DFS)求解结果进行对比，发现两种算法可行路径所得值相等，且对应的最优路径相同，因此，认为本文建立的协同优化模型可以得到最优的接驳公交线路路径和发车频率，模型是可行且有效的。