超大跨度自锚式悬索桥的动载试验研究

龚彦铭

(重庆市轨道交通(集团)有限公司，重庆 400000)

1 工程概况

鹅公岩轨道专用桥是重庆轨道交通环线二期工程重要的过江通道，距鹅公岩公路桥仅有45 m，是轨道环线连接主城南岸区和九龙坡区标志性工程。鹅公岩轨道专用桥为主跨600 m的双塔双索面自锚式悬索桥，全桥长1 650.5 m。主桥跨径布置为50 m+210 m+600 m+210 m+50 m，长1120 m。

主塔采用矩形双柱空心箱型结构，东、西塔高分别为163.9 m 和157.9 m，设置上、中、下3 道横梁；主梁为钢箱结构，梁高4.5 m，梁宽22 m，标准节段质量为408.6 t，共65 个节段；全桥共设两根主缆，每根主缆索由92 股φ5.3 mm×127丝平行钢丝构成。

2 试验目的

对体系转换后成桥状态下的主桥部分进行动力荷载试验，试验的主要目的：在动载试验作用下，测定桥跨结构的固有频率、振型及阻尼比，验证大桥的设计计算结果；检验桥梁在满载列车不同运行速度条件下的实际工作状态，测量在列车活载作用下桥跨结构构件控制截面的动应变，分析评价桥梁的动力系数和桥梁的刚度是否满足有关要求，为竣工验收提供重要的技术数据，为桥梁的运营及养护提供科学依据和指导[3-4]，为同类桥梁的施工、养护积累经验。

3 动力加载试验方案设计

3.1 动力荷载试验内容及其作用方式

1）动力特性试验：在桥面无交通荷载以及桥址附近无规则振源的情况下，测定桥跨结构由于桥址处风荷载、地脉动和水流等随机荷载激励而引起的桥跨结构微幅振动响应，获得桥梁结构的固有频率、振型和阻尼比。

2）无障碍行车试验：在桥面无任何障碍的情况下，采用两列山地城市As 型（7 节编组）满载列车分别以不同的速度（最大行驶速度为80 km/h）同向、对称、匀速驶过桥跨结构，测定桥跨结构在运行列车荷载作用下的动力反应。

3） 制动试验：采用两列山地城市As 型满载列车分别以30 km/h、50 km/h（根据荷载试验规范要求，制动试验的车速一般不大于50 km/h）的速度匀速行驶至测试断面时实施紧急制动，使其产生较大的制动力并对桥梁形成一定的冲击作用，以测得在制动条件下的动力响应。

3.2 测试项目及测试方法

1）固有频率、振型和阻尼比：通过拾振传感器、信号采集系统和计算机拾取并记录桥梁结构的随机振动响应[5]。

2）动应变：采用应变片及动态采集与分析系统进行测试，同时在东岸上下游阻尼器处布置位移传感，读取在不同工况下制动试验中阻尼器的纵向位移。

3.3 测试断面与测点布置

1）动力特性试验：纵桥向分别在锚跨段L/2 截面、边跨L/4 截面、中跨L/8 截面处布置加速度拾振器（L 为主桥跨径）。横桥向在每一截面的桥面上下游两侧布置竖向和纵向拾振器。测点布置如图1、图2 所示。

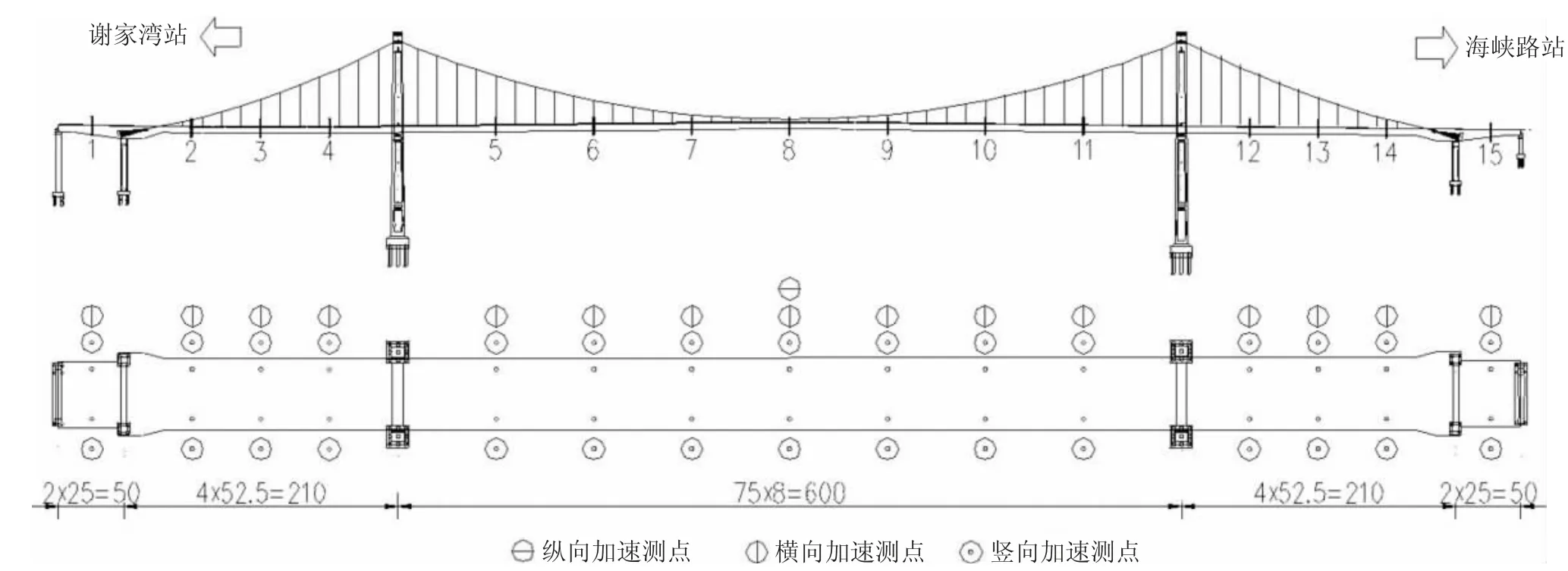
图1 纵梁测点立面、平面布置示意图

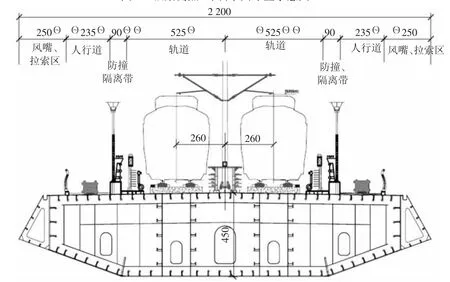
图2 纵梁测点横断面布置示意图（左侧为下游）

2）无障碍行车试验：分别在中跨A 截面（跨中）、B 截面（距东塔160 m 处）布置动应变测点，动应变测点布置如图3、图4 所示。

图4 A、B截面动应变测点布置示意图（单位：cm）

3）制动试验：本次试验用2 列满载列车分别以30 km/h 与50 km/h 的速度匀速行驶至跨中与L/4 截面时实施紧急制动，列车制动位置及阻尼器位移测点布置如图3、图5 所示。

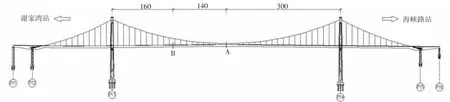
图3 主梁纵向动应变测试截面布置示意图（单位：m）

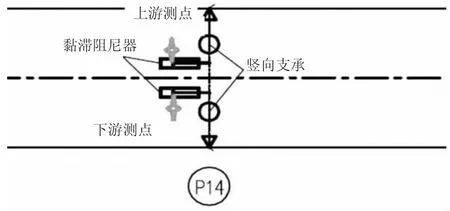
图5 阻尼器纵向位移测点布置示意图

3.4 动力特性理论分析

通过Midas Civil 建立空间有限元计算模型，如图6 所示，对鹅公岩轨道专用桥主桥进行特征值分析，考虑自重、二期恒载及相关横隔板的质量矩阵，提取前11 阶的振型及振动频率数据，如表1 所示。

表1 主桥动力特性计算值及振型图

图6 主桥空间有限元计算模型

4 动载试验结果分析

4.1 动力特性测试结果分析

通过对鹅公岩轨道专用桥主桥的模态测试数据进行时域及频域分析，得出鹅公岩轨道专用桥主桥的自振特性参数如表2 所示，结构频谱分析图形如图7、图8 所示，主桥部分实测振型如图9、图10 所示。

图7 横向频谱分析示意图

图8 纵向频谱分析示意图

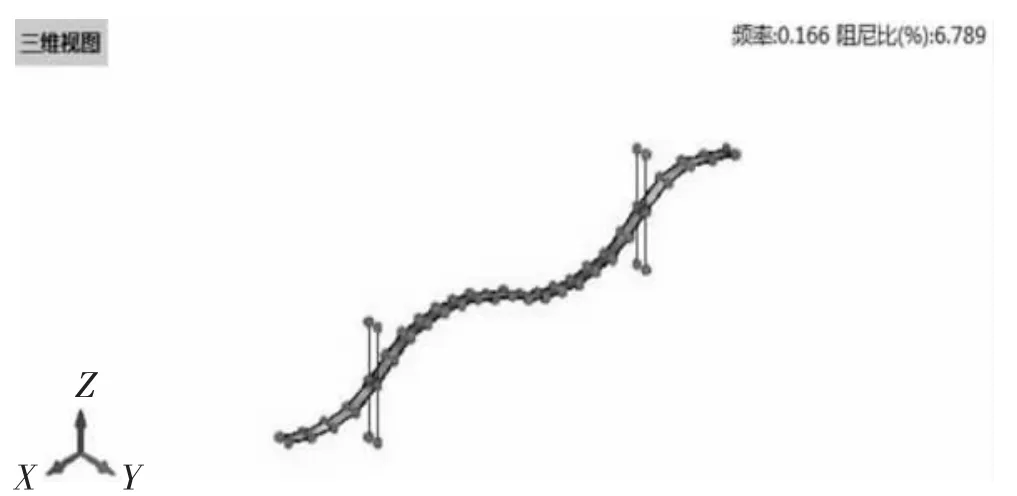
图9 主桥实测一阶竖弯振型图

图10 主桥实测一阶横弯振型图

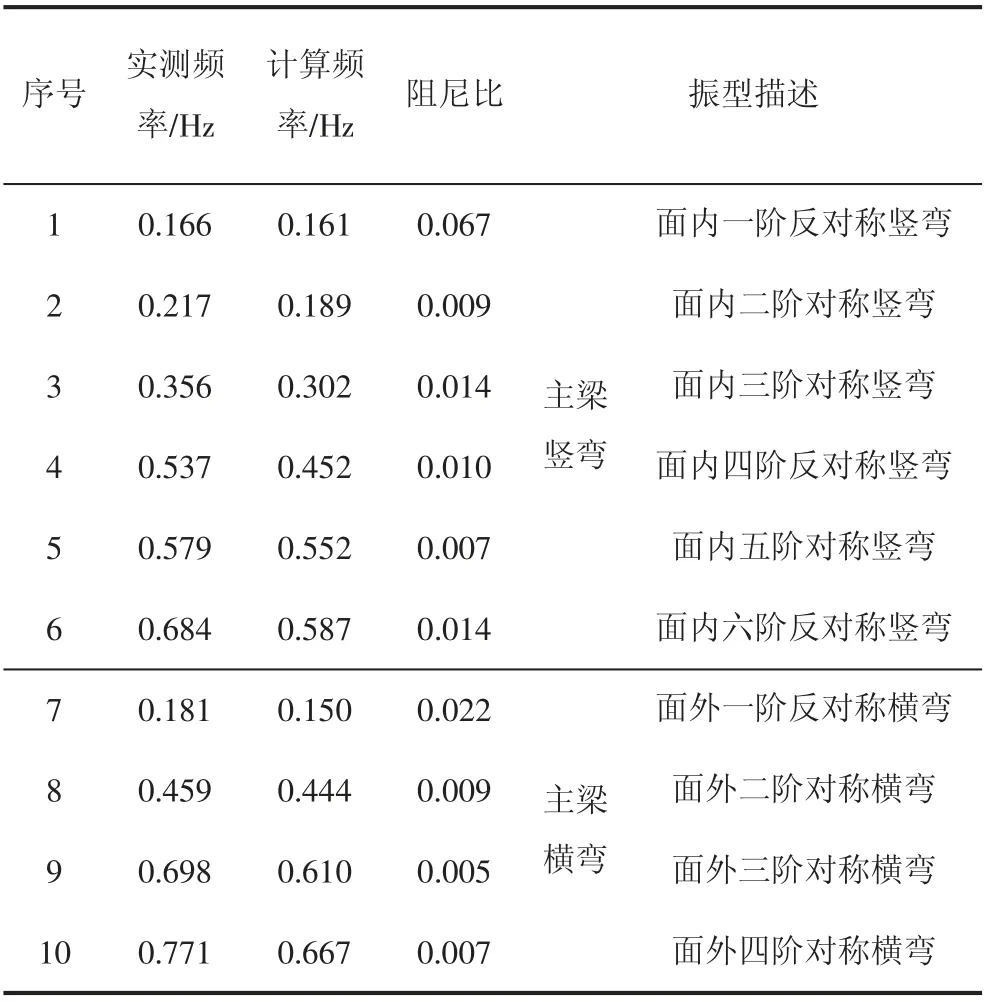
表2 主桥桥跨结构自振特性参数测试结果

从分析结果可以看出，鹅公岩轨道专用桥主桥的实测竖向基频为0.166 Hz，振型主梁面内一阶反对称竖向弯曲振动，阻尼比为0.067，计算频率为0.161 Hz；实测横向基频为0.181 Hz，振型为面外一阶对称横弯弯曲振动，阻尼比为0.022，计算频率为0.150 Hz；竖向、横向实测值均大于计算值，表明桥梁竖、横向动力刚度满足要求。

阻尼是振动系统在振动过程中由于外界作用或系统本身固有的原因引起的振动幅度逐渐下降的特性，实际结构系统的阻尼比较复杂，包括由于材料分子之间的摩擦引起的内阻尼、构件之间支承与连接部位的摩擦、振动时与周围介质(大气等)的相互作用引起的能量耗散等,实测本桥阻尼比在合理范围之内。

4.2 动力响应测试结果

4.2.1 无障碍行车试验跨中截面动应变测试结果

跨中截面动应变（测点1、测点3、测点5）峰峰值及动力系数测试结果如表3 所示，各列车激励下动应变部分时域信号曲线如图11、图12 所示。

图11 20 km/ h 跨中截面各测点动应变时域信号

图12 60 km/ h 跨中截面各测点动应变时域信号

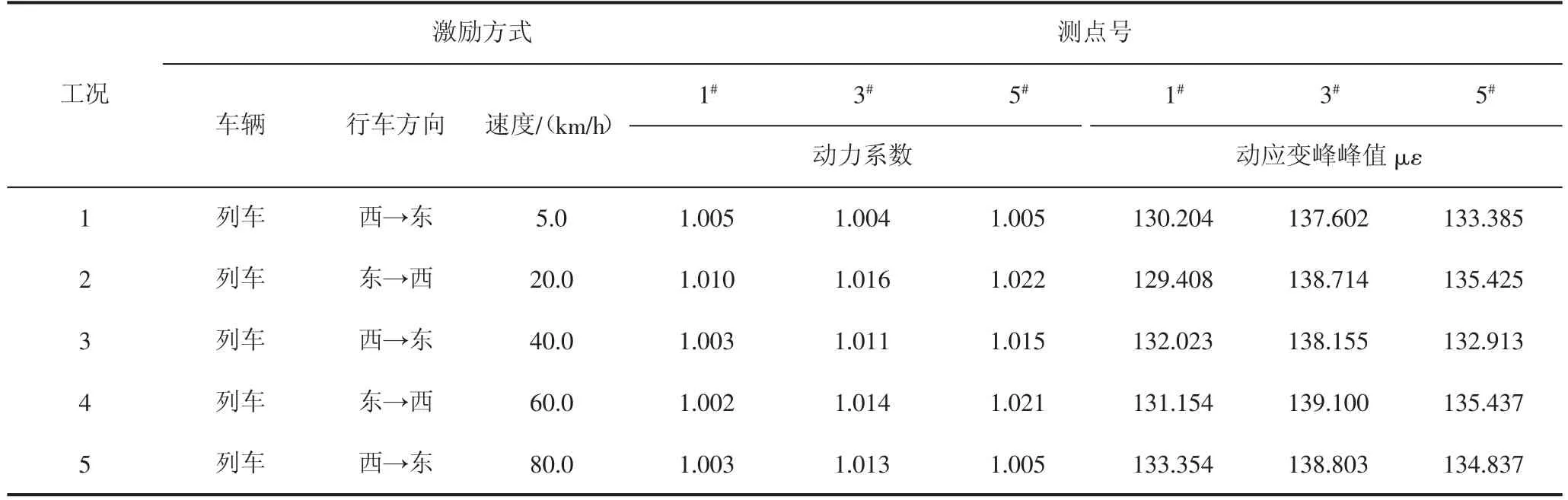
表3 跨中截面应变动力系数测试结果

由上述的跨中截面动应变测试结果表明：鹅公岩轨道专用桥主桥在以不同车速行车时，跨中截面动应变峰峰值在129.408 με~139.100 με，动力系数在1.002~1.022，平均动力系数为1.010，实测动力系数小于相应理论计算值（按规范计算的动力系数为1.035），满足规范要求。从测试结果来看，跨中截面在车速20~60 km/h 时动力系数较大。

4.2.2 无障碍行车试验L/4 截面动应变测试结果

L/4 截面动应变（测点1、测点3、测点5）峰峰值及动力系数测试结果如表4 所示，各列车激励下动应变部分时域信号曲线如图13 所示。

表4 L/ 4 截面应变动力系数测试结果

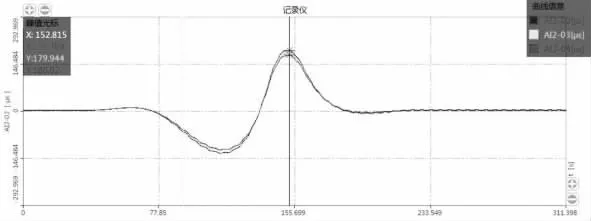
图13 20 km/ h 时L/ 4 截面各测点动应变时域信号

由上述的L/4 截面动应变测试结果表明：鹅公岩轨道专用桥主桥在以不同车速跑车时，L/4 截面动应变峰峰值在171.495 με~194.572 με，动力系数在1.001~1.011，平均动力系数为1.003，实测动力系数小于相应理论计算值（按规范计算的动力系数为1.035），满足规范要求。

从测试结果来看，L/4 截面在车速20 km/h 时动力系数较大，动力系数总体小于跨中截面。总体而言，动力系数与车速相关性不明显。

4.2.3 制动试验测试结果

本次试验用两列满载列车分别以30 km/h（自西向东）、50 km/h（自西向东）的速度匀速同向行驶至测试断面（跨中和L/4 截面）时实施紧急制动，使其产生较大的制动力并对桥梁形成一定的冲击作用，测得在制动条件下的部分动应变时域信号曲线如图14、图15 所示，测得在制动条件下的加速度时域曲线如图16~图19 所示。测得的东塔侧加劲梁底阻尼器的纵向位移见表5。

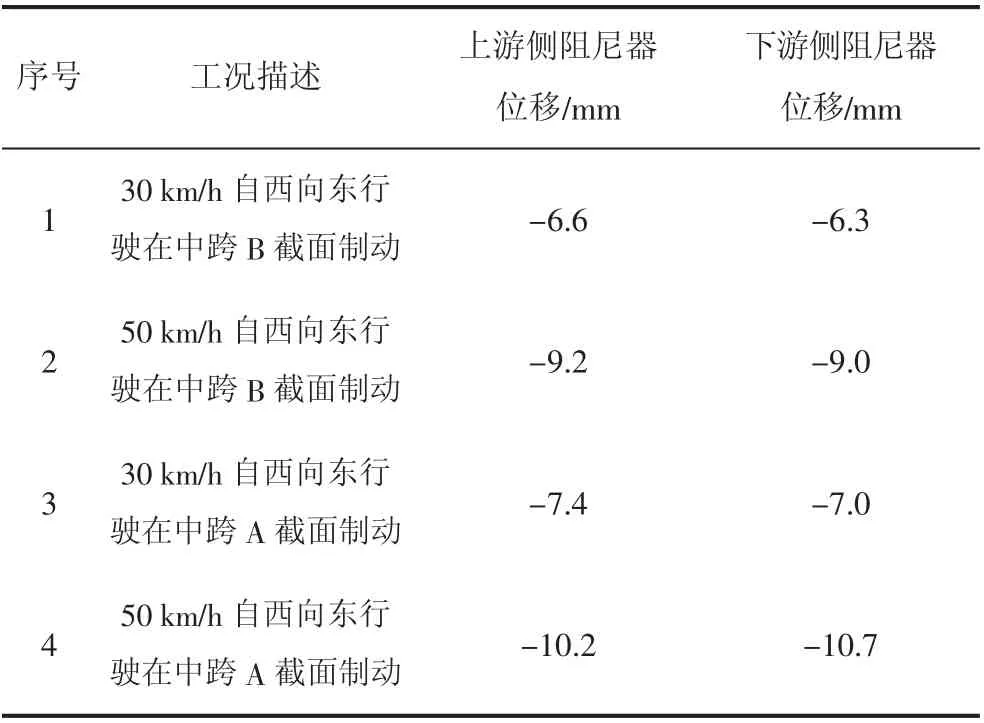
表5 制动试验的阻尼器位移量测试结果

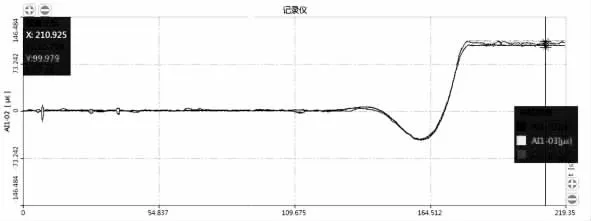
图14 30 km/ h 制动跨中截面动应变时域信号

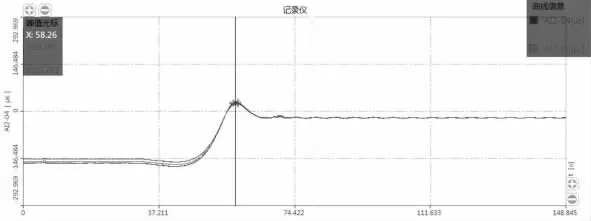
图15 50 km/ h 制动L/ 4 截面动应变时域信号

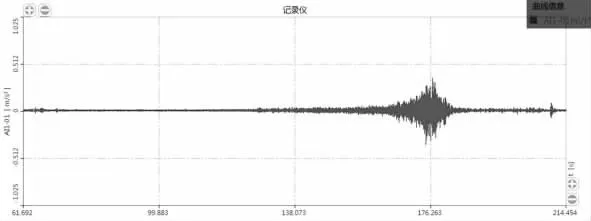
图16 30 km/ h 跨中制动加速度时域及频域信号

图19 50 km/ h 制动L/ 4 截面加速度时域及频域信号

4.3 试验前后主桥外观检查对比

通过对试验前后主桥钢箱梁、缆索系统、索鞍、主塔、支座等外观检查，未发现异常现象，结构处于稳定状态。

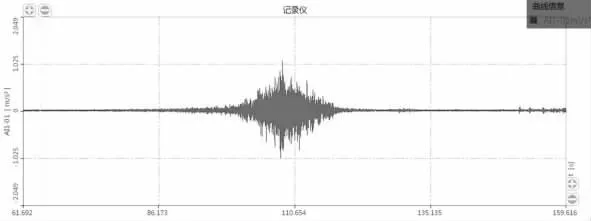
图17 50 km/ h 跨中制动加速度时域及频域信号

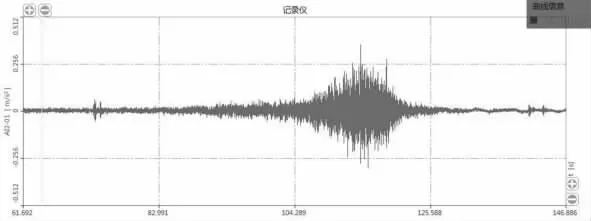
图18 30 km/ h 制动L/ 4 截面加速度时域及频域信号

5 结论

通过对鹅公岩轨道专用桥主桥进行试验模态测试获得了结构的整体振动特性参数，通过对桥梁结构及列车在多工况行车激励下的动力响应测试，获得了主桥桥跨结构控制部位动应变、动力系数、加速度时域曲线，同时对主桥的振动特性进行了有限元分析并与试验结果比较，并结合试验前后主桥各系统的外观检查，得出：

1）实测得到的主桥各阶固有振动频率均比相应模态的理论计算值大，表明桥梁实际竖、横向整体刚度优于理论刚度。

2）主桥各阶振型阻尼比为0.005～0.067，为小阻尼振动，实测阻尼比正常。

3）主桥L/4 截面在以不同车速跑车时，动力系数在1.001~1.011，平均动力系数为1.003；跨中截面在以不同车速跑车时，动力系数在1.002~1.022，平均动力系数为1.010，实测动力系数均小于相应理论计算值（1.035），实测桥梁动力系数正常。

4）行车试验及制动试验结果表明，主桥动力响应正常。