大断面矩形顶管近穿既有地铁隧道数值模拟分析

刘庆方，汪 洋，郝宇航，朱启银，况联飞

（1. 中铁隧道勘测设计院有限公司，天津 300133；2. 中铁二局第四工程有限公司，四川 成都 610306；3. 中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221116）

0 引 言

随着我国经济快速发展，城市建设步伐不断加快，城市地下空间的开发与建设需求日益旺盛。在地下管网规范化建设的大背景下，传统开挖式地下管道和人行通道施工技术难以满足日趋严格的工程建设需求。因而对地表小开挖、不影响现有交通等方面具有显著优势的顶管施工法应用日益广泛[1-3]。其中矩形顶管相较于圆形顶管可节约 20%以上空间，能更充分利用结构断面，对覆土的厚度要求更小，可降低顶管下穿时的深度和坡度，因而应用更为广泛。然而，顶管施工对周围环境的影响不容忽视，研究顶管施工对现场周围环境的影响，进而提出控制措施保证施工安全已经成为了研究热点[4]。

郭亮[5]对郑州某顶管下穿工程的土体监测数据研究发现顶管施工过程中，控制土体沉降应将进出洞区域进行土体加固同时减少停机等待时间。刘波等[6]采用微欠挖工艺保证实际出土量比理论出土量少2%～5%，有效控制了隧道隆起和地表沉降。有限元分析可在施工前对施工全过程进行模拟，对施工方案进行验证，正逐步成为辅助工程施工的重要手段。黄建华等[7]利用有限元软件模拟研究滨海软土浅埋矩形顶管施工过程，结合现场沉降观测数据获得了顶管顶进过程中地表的沉降变形以及顶管应力变化规律。叶耀东[8]利用有限元模拟软件对地铁变形控制措施进行比选，发现直接顶进稍有不慎极容易超出地铁隧道保护标准要求。赖金星等[9]利用ANSYS软件进行顶管施工模拟得出地层损失是引起土体沉降的主要原因。郝小红等[10]进行数值模拟得出顶管施工对地层土体位移的影响主要集中在顶管两侧矩形顶管截面长边两倍的长度范围内。薛青松[11]修正改进比尔鲍曼理论，推导出大断面矩形顶管掌子面推进力的新计算方法，并在实测中取得较好的效果。

然而，超大断面矩形顶管近距离上穿既有隧道时，地铁隧道变形和地表沉降控制机理，以及如何做好施工风险管控仍然是当前矩形顶管施工的重点和难点。为此，本文以无锡震泽路过街人行通道超大顶管上穿既有地铁隧道为工程背景，利用有限元程序 PLAXIS 3D对顶管施工全过程进行数值模拟分析，研究不同因素对隧道结构以及地层沉降的影响规律，为顶管施工安全管控提供指导依据。

1 工程概况

无锡震泽路过街顶管通道位于震泽路与清舒道十字路口，呈南北走向，顶管施工由南向北横穿震泽路。通道北侧为无锡太湖国际博览中心，上跨无锡地铁四号线（尚未铺轨）丰润道站—博览中心站区间隧道，南侧为一处空旷拆迁工地。其平面位置及周边环境见图1。

图1 场地平面图Fig. 1 Site layout plan

该过街通道顶管长 50.62 m，管节外包尺寸为9.8 m×5.2 m（宽×高），壁厚700 mm，采用C50/P10预制管节，管节宽度为1.5 m，重约71.4 t。顶管通道近距离上穿无锡地铁4号线地铁隧道，最近点仅为2 m，如图2所示。通道两端设置顶管始发井和接收井各一座，地铁隧道右线和左线距离始发井的距离分别为12.9 m，30.4 m，通道与四号线地铁隧道的相对位置如图2所示。

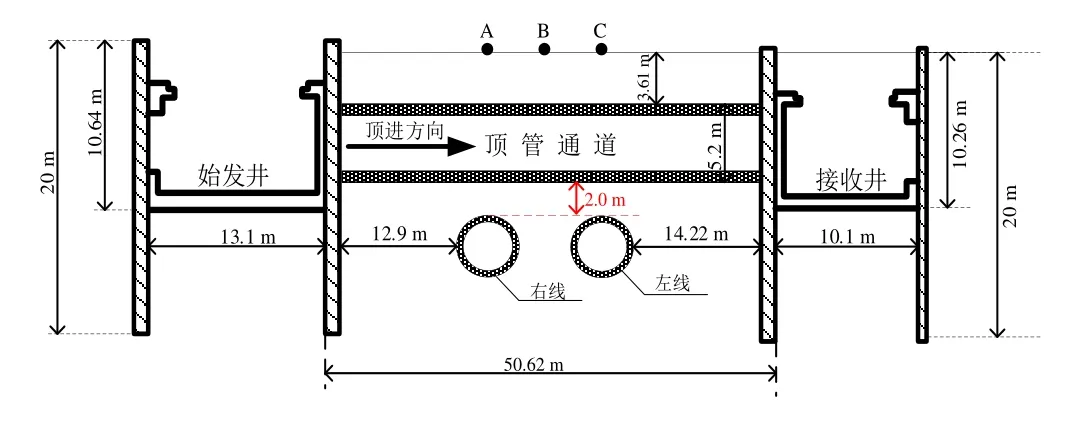
图2 顶管通道剖面图Fig. 2 Section of pipe jacking channel

2 数值模拟分析

2.1 三维模型建立

基于有限元软件PLAXIS 3D建立三维模型模拟顶管施工全过程，对施工过程中地表变形特征以及既有地铁隧道的结构变形规律进行分析。结合类似工程经验，大断面顶管施工对土体应力影响范围为顶管断面高度和宽度中较大值的 3～5倍，因此模型范围取为高45 m，宽80 m，沿轴线方向的长度为150 m。模型边界约束采用左右两侧水平方向约束，下部边界设水平、竖向约束，上部边界为自由边界。土体使用三维实体单位进行模拟，顶管和隧道使用板单元进行模拟，整个模型单元总数234 619个，节点总数365 106个。根据设计方案中土层情况、顶管施工、区间隧道分布以及荷载信息，整体模型如图3所示。

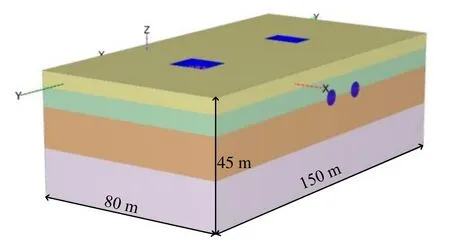
图3 模型示意图Fig. 3 Schematic diagram of numerical analysis model

2.2 模型参数选取

始发井和接收井结构采用板单元进行模拟，弹性模量取为20 GPa，泊松比取0.2。顶管和隧道管片几何尺寸与实际管片一致，材料均为C50混凝土，模拟采用线弹性模型，密度取2 500 kg/m³，弹性模量取34.5 GPa，泊松比取0.2。结合勘察报告，本工程场地内地基土属于第四系（Q4）沉积地层，涉及土层由上至下依次为：杂填土、粉质黏土层、粉质黏土夹黏质粉土层、黏质粉土夹粉质黏土层。土体模拟采用摩尔-库伦模型，各土层模型参数见表1。顶管始发加固长度和顶管接收加固长度均为6 m，加固宽度均为顶管结构每侧3 m，竖向加固范围均为地面到顶管结构底4 m，与未加固地层相比，加固体弹性模量增大一倍。顶管和隧道模拟适当简化，假设其为均质材料，忽略管间连接部位刚度弱化影响。

表1 土层模拟参数取值Table 1 Soil layer parameters in numerical simulation

2.3 顶管顶进模拟及工况条件

为保证与顶管施工的实际工作性状接近，顶管顶进过程按照实际工况条件模拟，共分为5个阶段：（1）平衡地应力；（2）生成左右线隧道；（3）生成始发井和接收井；（4）位移重置；（5）顶管开挖。顶管开挖划分为33个施工段，施工段按照1.5 m一段进行划分，模型结构示意图及对应顶管顶进工况如图4所示。顶管施工时，管片拼装在始发井中而不再掘进机尾部，故而在模拟时掘进机与后续管片为连续连接。由于模拟的施工步较多，这里仅保留关键工况的模拟结果进行分析。工况1代表顶管顶进距离6 m；工况2代表顶管顶进距离15 m，该工况完成上穿右线；工况3代表顶管顶进距离33 m，该工况完成上穿左线；工况4代表顶管顶进49.5 m，即顶管上穿隧道完成。需要说明的是，顶管顶进施工工序复杂，难以全部纳入分析，本文研究主要考虑掌子面推力（50 kPa、100 kPa和200 kPa）、地层损失率（0%，0.1%，0.2%）和顶管内部配重（20 kPa、50 kPa、100 kPa）等施工因素，其中地层损失通过Plaxis平台提供的土体收缩率来模拟[12]。

图4 顶管模型结构示意图及顶进工况Fig. 4 Pipe jacking model and conditions

3 地表沉降与隧道结构变形分析

为研究顶管顶进过程地表竖向位移和隧道结构变形空间特征，本节模拟考虑施工参数为：掌子面推力200 kPa、地层损失率0.1%和顶管内部配重50 kPa。

3.1 顶管顶进对地表竖向位移的影响

顶进模拟时既有隧道开挖及始发井、工作井施工产生的位移变形已重置为 0，因此计算结果中的变形及沉降均为顶管顶进引起。为分析不同计算工况顶管顶进过程对地表沉降的影响，选取图2所示A、B、C三点分析顶管顶进过程地表沉降特征。A点和C点位于左右线隧道正上方地表，B点位于A和C中间。图5（a）为三点沉降随顶管顶进过程的变化规律，可以看出，每一测点均经历先隆起后沉降过程，C点的最终沉降量略小于A和B点。此外，选取图1所示的横纵线a和b进行不同顶进工况下的地表沉降空间特征分析，其中纵线b为顶管顶进的中心线，长度为始发井和接收井之间距离，a线垂直于b线，为始发井和接收井的中心线。对应顶管顶进过程4个工况的地表a、b线位置地表沉降分布见图5（b）和（c）。图5（b）表明顶进过程中，顶管机刀盘前方土体受掌子面推力影响而受挤压，有较小隆起变形，隆起最大值为1.80 mm；顶管机后方因出土卸荷以及地层损失而出现地表沉降，最大沉降量达到11.40 mm。图5（c）表明顶进过程中，顶管机前方土体隆起，后方土体沉降，顶管施工对地表变形的影响由顶管中心向水平两侧递减，沉降最大值始终位于顶管掘进中心线上方。

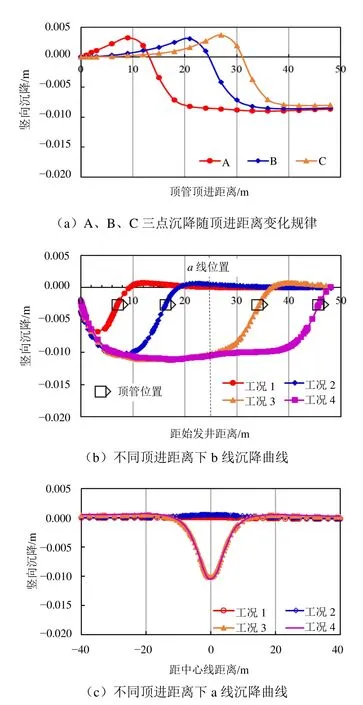
图5 不同工况下地表时空沉降特征Fig. 5 Settlement curve of cross and vertical section under different conditions

3.2 顶管顶进对既有地铁隧道的影响

顶管上穿既有地铁隧道，随着顶管通道内土体的开挖，周围土体应力场向通道内释放，进而引起隧道隆起。顶管上穿隧道后，右线和左线隧道最大隆起值分别为2.76 mm和3.97 mm，表现为后穿越的左线隧道隆起量大，这可能与先隆起的右线隧道叠加影响有关。如图6（a）所示，受影响隧道主要在顶管通道的投影区域，通道投影区域以外的隧道受影响较小，变形的影响由通道正下方向通道边线以外区域递减，距离通道的距离越远，所受的影响越小，左线和右线隧道的变形规律基本是一致的。

图6 顶管上穿既有隧道后隧道变形情况Fig. 6 Tunnel deformation after pipe jacking passes through the existing tunnel

顶管顶进过程中，既有隧道的竖向位移变形为隆起变形，水平向表现为向接收井一侧变形。管径表现为水平方向被压缩，竖直方向被拉伸，如图6（b）所示。因此，为保证隧道结构安全，探究施工参数对隧道位移的影响，并采取相应的隧道加固措施和减少隆起措施必不可少。

4 顶管施工参数影响分析

4.1 掌子面推进力的影响

大量工程实践表明，顶管掘进机正面推进力大小对地表和既有隧道变形有着重要影响[5-7]。为研究开挖面支撑力对地表和隧道变形的影响，计算了顶管刀盘前部推进力分别为 50 kPa、100 kPa和200 kPa，推进力梯度为20 kPa/m时顶管施工对地层沉降的影响。不同掌子面压力下地表b线沉降特征如图7所示。可见，随着掌子面正推力的增大，地表b线沉降呈减小趋势。根据掌子面推力的变化对地表竖向沉降的变化曲线可得在出土量相同的情况下，随着正推力的增大，地表的隆起增大，沉降减小。为进一步探究掌子面推进力对下部既有隧道变形的影响，计算出掌子面推进力在50～200 kPa的范围内，地层损失在0%、0.1%、0.2%条件下，下部既有隧道最大总位移量值变化如图8所示。可见，在保证地层损失相同的情况下，随着掌子面正面推进力的增加，隧道最大的位移量会增加，隧道受到的影响增大。由此可知，掌子面推力的大小并不是唯一的影响因素，地层损失的影响也应加以考虑。

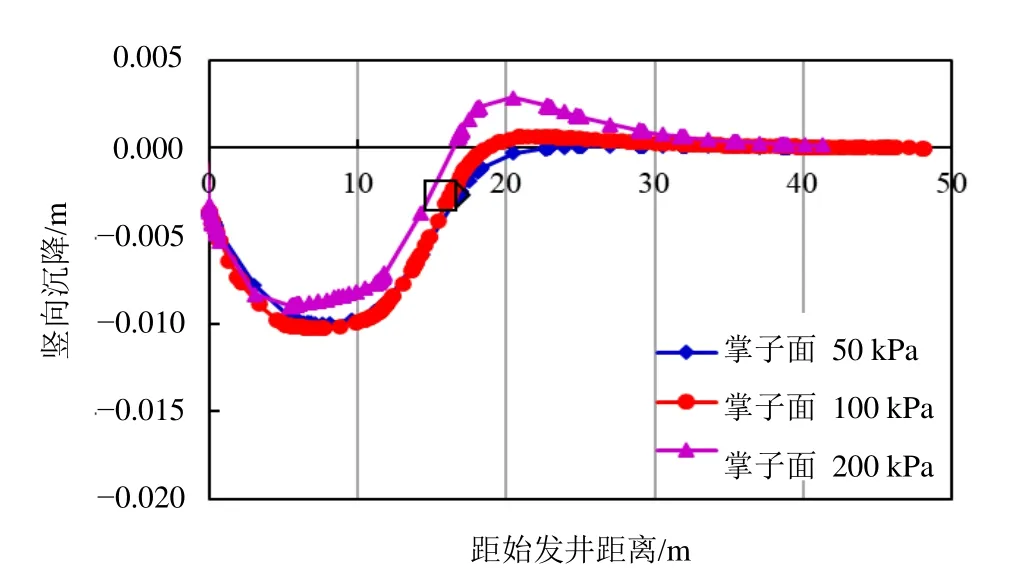
图7 正推力对b线地表沉降的影响（工况2）Fig. 7 Variation of surface settlement along the middle line of pipe jacking with propulsive force

图8 隧道最大位移随正推力变化曲线Fig. 8 Variation of maximum displacement of existing tunnel with propulsive force

4.2 地层损失的影响

地层损失是实际开挖土体体积和竣工顶管体积之差，常以占理论排土体积百分比的地层损失率表示，是顶管施工造成土体变形的根源所在。本文考虑3种地层损失率（0%，0.1%，0.2%）对地表沉降的影响规律。顶管顶进工况2下顶管中线地表b线沉降如图9所示，由沉降曲线可知，将地层损失从0%提升到0.2%，顶管掌子面前的土体几乎不受影响，但掌子面后土体的沉降会随着地层损失的增大而增加，从8.58 mm增加至11.10 mm。因此，地层损失作为影响竖向沉降的重要因素在实际施工时应加以控制，以保证地层损失率处于一个较低的水平。

为研究地层损失率对既有隧道变形的影响，同样在地层损失率在 0%、0.1%、0.2%条件下，考虑掌子面推力计算既有隧道的最大位移量，如图10所示。在掌子面推力相同的情况下，地层损失率从0%提升到 0.2%，隧道最大位移量的变化不超过1 mm，因此，地层损失率对隧道位移影响较小。

图9 地层损失对b线地表沉降的影响（工况2）Fig. 9 Variation of surface settlement along the middle line of pipe jacking with soil loss

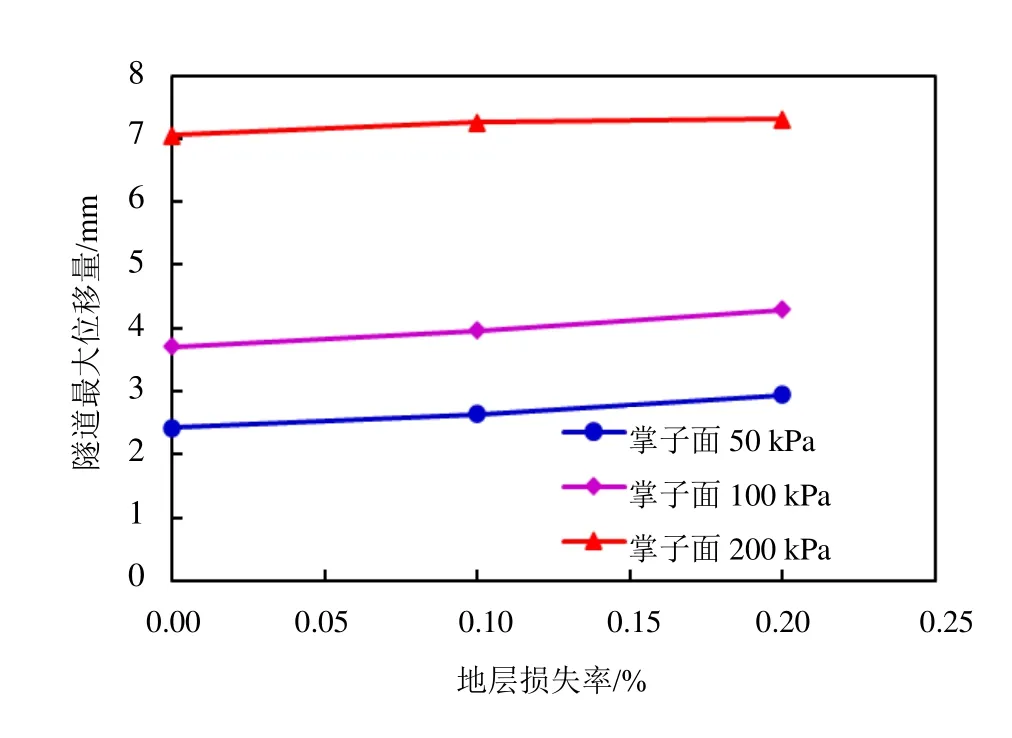
图10 隧道最大位移随地层损失率变化曲线Fig. 10 Variation of maximum displacement of existing tunnel with soil loss rate

4.3 顶管内配重的影响

由于顶管内施加配重可控制既有隧道隆起及控制顶管上浮。因此，顶管施工时通常会在顶管通道内进行堆铁配重即压重。为探究堆铁配重的影响，在20 kPa、50 kPa、100 kPa的压重条件下，提取工况2对应的地表b线竖向沉降曲线以及隧道最大竖向位移如图11和图12所示。结果表明，对于掌子面后地表土体，随着顶管内压重的增加，土体竖向沉降随之增加。而对于掌子面前的地表土体，随着压重的增加土体竖向隆起随之减小；压重达到100 kPa时，掌子面前方地表土体甚至由隆起转变为沉降。将掌子面推力从50 kPa上升到200 kPa，隧道的最大竖向位移变化小于1 mm，可见隧道的竖向位移受掌子面推力影响较小。在相同掌子面推力的情况下，压重20 kPa时隧道表现为隆起，随着压重增加隆起值不断减小；压重100 kPa情况下，隧道变形转变为沉降。

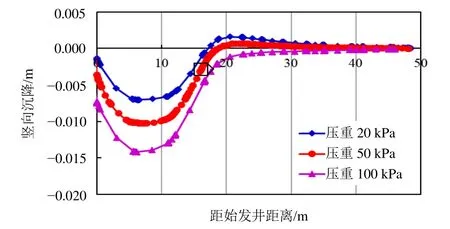
图11 压重对b线地表沉降的影响（工况2）Fig. 11 Surface vertical settlement under the action of ballast

图12 隧道最大位移随压重变化曲线Fig. 12 Variation curves of maximum displacement of existing tunnel with ballast

5 结 论

本文基于数值模拟手段，系统分析了大断面矩形顶管近距离上穿既有地铁隧道时地表及隧道结构变形影响规律，研究获得的主要结论如下：

（1）顶管顶进过程中，地表经历了先隆起后沉降的过程，隆起最大值达1.8 mm，沉降最大值始终位于顶管掘进中心线上方，最大沉降量达到11.40 mm。既有隧道的竖向位移变形为隆起变形，水平向表现为向接收井一侧位移。左右线隆起最大值介于2.76～3.97 mm之间。

（2）顶管顶进过程中掌子面推进力对地表土体以及既有隧道的影响较大。随着掌子面推进力的增大，掌子面前方地表土体隆起增大，后方地表土体沉降减小，既有隧道的位移也随之增大。因此为保证施工质量，施工时应严格控制顶管推进力。

（3）顶管顶进过程中，地层损失会影响地表土体沉降。地层损失越多，地表土体沉降越大，但地层损失对既有隧道的影响微乎其微。利用地层损失的影响规律采用合理的施工方法，如“微欠挖”可对地表沉降进行控制。

（4）顶管内压重可作为稳定顶管、防止顶管上浮的有效手段，但过大的压重会加剧地表土体以及既有隧道的沉降，因而施工时应严格控制。