基于方差分析的环境试验的影响因素分析

刘凯，刘展，石远豪，刘青林，区汝俊，马京瑞，冯达安，林丽芸

（佛山赛宝信息产业技术研究院有限公司,广东 佛山 528226）

0 引言

环境试验的目的是验证材料或产品是否达到了在研发、设计、制造中预期的目标，具体的实施方法是在试验中施加一种或几种综合性的应力来考核其对材料或产品的影响，目前环境模拟设备及方法已基本趋于成熟，可靠性模型及寿命预计也逐步地发展起来，但是，对如何分析环境试验结果的研究还相对比较少[1-2]，评价单因素及多因素对环境试验结果的影响方面还有待完善。本文通过F分布中的显著性检验，探讨单因素进而引申到多因素影响条件下的量化影响。

1 抽样分布函数

方差分析是基于统计基础之上，需要足够的数据进行支撑。在数据分析的过程中，观测到的总是样本，通过样本来推断总体是统计分析的基本特点，它不可能百分之百正确，因此存在概率问题。统计量是样本的函数，它是一个随机变量，统计量的分布被称为抽样分布，常见的有正态分布和三大抽样分布。

1.1 正态分布

正态分布又名高斯分布，两头低，中间高，左右对称；因其曲线呈钟形，常称之为钟形曲线，曲线形状如图1所示。

图1 正态分布曲线

若随机变量X服从一个位置参数为μ、尺度参数为σ的概率分布，且其概率密度函数为：

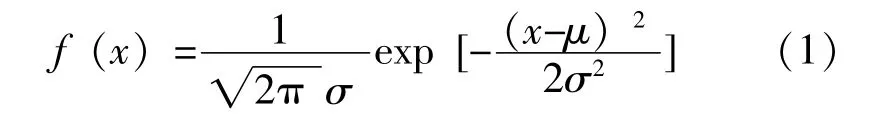
式（1）中：μ——正态分布的数学期望；σ2——正态分布的随机变量的方差；

±σ——曲线的拐点，σ越小，曲线越尖。

1.2 χ2分布(卡方分布)

设X1，X2，…，Xn是来自正态总体N（0，1）的样本，则称统计量χ2=X21+X22+…+X2n为服从自由度为n的χ2分布，其概率密度函数为：

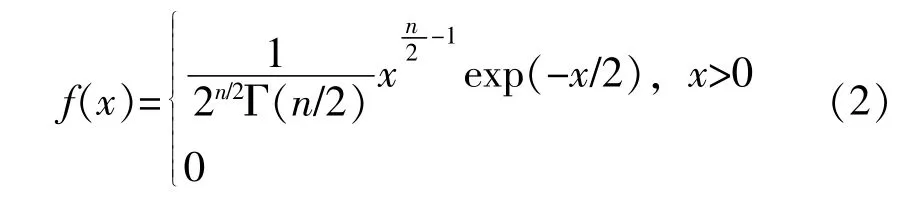
χ2（n）分布的数学期望和方差：E（χ2）=n，D（χ2）=2n。

1.3 t分布(学生分布)

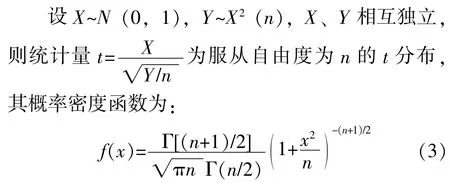
当n足够大时，t分布近似于N（0，1）分布；n较小时，两者相差很大。

1.4 F分布

对给定的α（0<α<1），称满足条件P（F>Fα（n1，n2））=α的点Fα（n1，n2）为F分布上的a分位点，如图2所示。

图2 F分布上的α分位点

2 单因素方差分析

ANOVA是由英国统计学家R.A.Fisher首创，为纪念Fisher，方差分析又被称为F检验[3]，主要是用于推断多个总体均数有无差异，即检验因素对指标是否会产生影响。

设μ1、μ2、μ3、μ4分别为某一因素水平下的指标水平，也就是检验下面的假设：

1）H0:μ1=μ2=μ3=μ4（原假设）；

2）H1:μ1、μ2、μ3、μ4不全相等（备择假设）。

检验上述假设所采用的方法就是方差分析。

设因素A有m个水平，在每个水平下，进行r次独立试验[4]，得到如表1所示的结果。

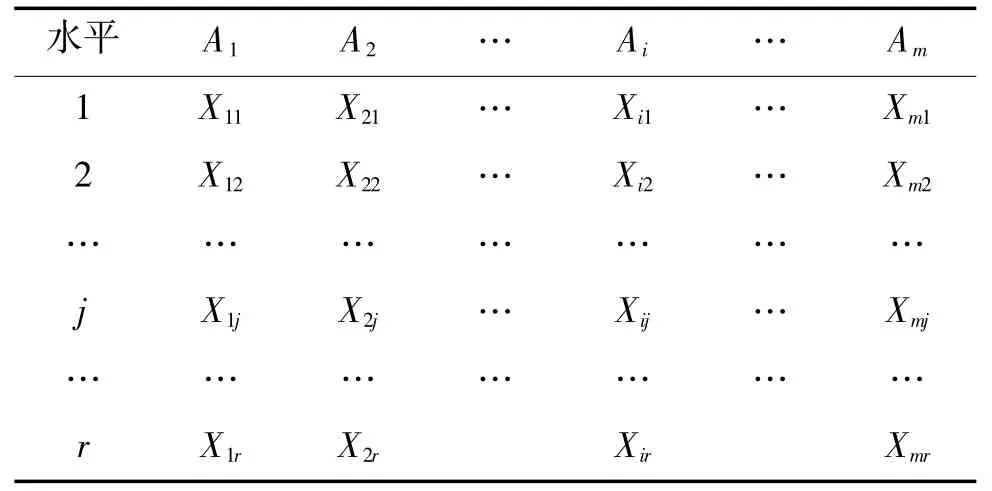
表1 方差分析结果

假设各个因素A1、A2…Am水平下的样本X1j、X2j…Xmj来自具有相同方差σ2，均值分别为μ1，μ2，…，μm的正态总体N（μj，σ2），且不同水平下的样本之间相互独立，则方差分析的任务即是检验以下假设：

1）H0：μ1=μ2=μ3=μ4（原假设）；

2）H1：μ1、μ2、μ3、μ4不全相等（备择假设）。

表格中的数据是参差不齐的，数据波动的可能原因来自两个方面：

1）由于因素的水平不同，因素的水平变化引起的试验数据波动成为条件误差；

2）来自偶然误差，由随机因素引起的试验数据波动被称为随机误差。

a）误差的表示方法

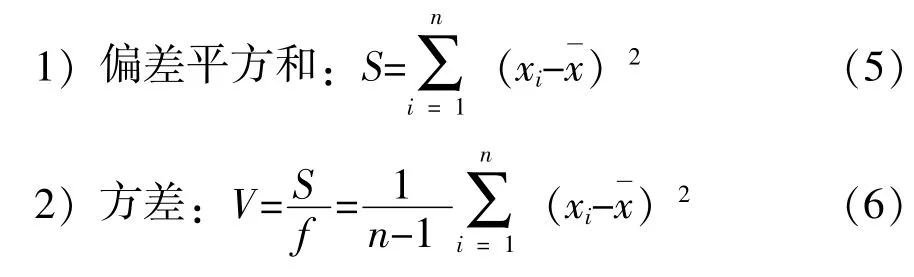
从随机因素与试验条件改变所形成的总方差中，将属于试验误差范畴的方差与由于试验条件改变而引起的条件方差分解出来，将两类方差在一定的置信概率下进行F检验，就可以确定因素效应对试验结果的影响程度。

b）计算平均值

e）F检验

均方之比FA=VA/Ve是一个统计量，服从自由度为（fA，fe）的F分布。

如果FA的值小于某一临界值，说明因素A水平的改变对试验指标的影响与试验误差对试验指标的影响接近，认为因素A水平之间没有显著的差异或因素对指标的影响不显著；如果FA的值大于某一临界值，说明因素A水平的改变对试验指标的影响显著。

显著性水平α一般取0.01、0.05、0.10，α越大，犯弃真错误的概率越大，说明H0更有可能是真的，并且因素水平之间的差异越小；α越小，犯弃真错误的概率越小，说明H1更有可能是真的，并且因素水平之间的差异越大。

α=0时，犯弃真错误的概率是0，若F非常大，H0成立的概率几乎为0，说明因素之间确定一定以及肯定有差异，即差异相当大。

若F>F0.01（f1，f2），犯弃真错误的概率小于1%，说明因素之间的差别非常大。

若F0.01（f1，f2）>F>F0.05（f1，f2），犯弃真错误的概率在1%~5%，说明因素之间的差别比较大。

若F0.05（f1，f2） >F>F0.1（f1， f2）， 犯弃真错误的概率在5%~10%，说明因素之间有差别。

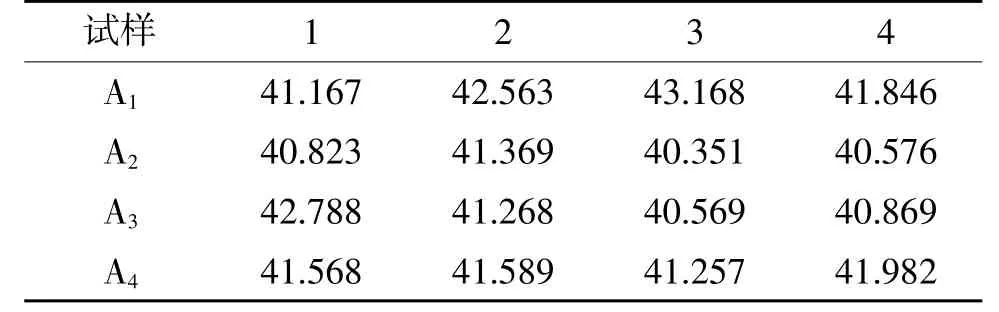
若F

α=1时，Fα（f1，f2）=0，犯弃真错误的概率是100%，说明因素之间确定一定以及肯定没有差别。

制定方差分析表，如表2所示。

表2 方差分析表

3 环境试验实例

现随机抽取厂家生产的A1、A2、A3、A44种金属片状试样，按照GB/T 10125标准进行中性盐雾试验[5]，试验条件如表3所示。

表3 中性盐雾试验条件

试验结束后，进行腐蚀产物的去除操作及试样称重，试样的质量损失如表4所示。

表4 盐雾试验后的质量损失数据单位:g/m2

数据列表计算，结果如表5所示。

表5 数据计算结果

故4种金属片状样品盐雾试验后的结果有一定差别。

4 结束语

本文以盐雾试验为例，详细地介绍了单因素方差分析方法在环境试验中的应用，将因素的影响通过量化表示出来，后续可推广到双因素及多因素下的方差分析，但是要注意的是，要考虑多因素下不同影响因素之间的交互作用，针对有交互作用的情况需要进行重复试验，运用方差分析工具可以帮助工程人员更好地分析因素对实验结果的影响，从而为研发及改进样品提供数据支撑。