基于CPSO算法的轨道交通供电系统运行优化研究

王忠有，莫 超，冯 诚，覃龙飞

0 引言

随着经济的快速发展和城市现代化水平的提高，城市居住人口逐渐增大，日益增长的城市人口一方面促进了城市建设，另一方面也增加了城市的负担[1]。寻找一种安全可靠、舒适便捷、运量大且污染小的城市交通工具，已经成为世界各国城市发展面临的主要课题。地铁正是现代化城市中最理想且能满足市民出行需求的一种重要交通工具。

但是，随着地铁的大规模建设与发展，其日常运营能耗占据城市电网能耗的较大比重，因此，已有学者将研究的重点放在轨道交通节能运行问题上[2，3]。降本增效不仅符合国家绿色发展的政策，也是轨道交通运营的主要目标之一，同时，城市轨道交通行业的节能措施在国家“碳中和”、“碳达峰”的进程中应更多地承担节能减排责任。

本文重点研究在确保系统可靠运行的前提下，通过相应的调压手段优化供电系统的电压质量，减少线路损耗，降低运行成本，提高经济效益。最后通过南宁轨道交通3号线实例分析，验证该优化策 略的有效性与经济性。

1 轨道交通供电系统建模与潮流计算分析

1.1 轨道交通中压供电系统模型

轨道交通中压供电系统由35 kV电缆线路连接构成，电缆沿轨道交通区间线路敷设，通过35 kV环网电缆将主变电所和牵混所、降压所连接成完整的供电系统，如图1所示。

图1 轨道交通35 kV环网系统

1.2 轨道交通供电系统潮流计算与分析

电力系统是一个复杂且庞大的系统，针对电力系统的分析和计算通常以交流系统潮流计算为依据，而交流潮流计算一般针对的参数是多元、多次，方程为非线性，这种多元的非线性方程给求解潮流带来了很大困难。从数学角度来解决问题可以带来不同的思路，牛顿-拉夫逊法[4]是数学上求解非线性方程式的一种最常见的有效方法，有较好的收敛性，被广泛用于电力系统潮流计算，潮流计算流程如图2所示。

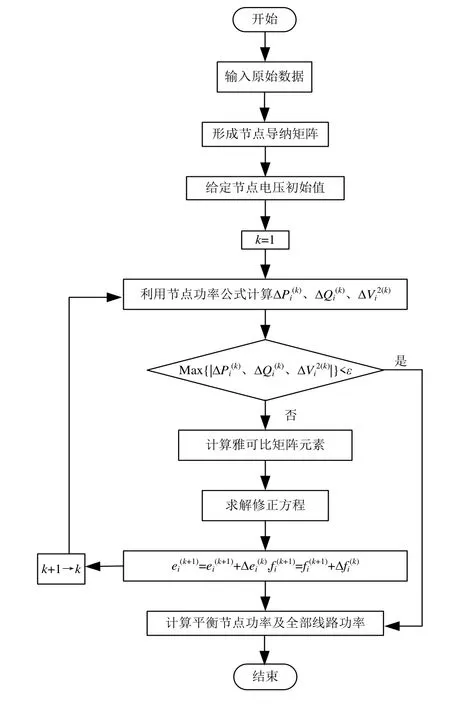
图2 潮流计算流程

2 轨道交通交流供电系统优化运行模型

2.1 目标函数

在保证电压不越限的情况下，通过采用线路损耗最小为目标函数进行优化，具体为

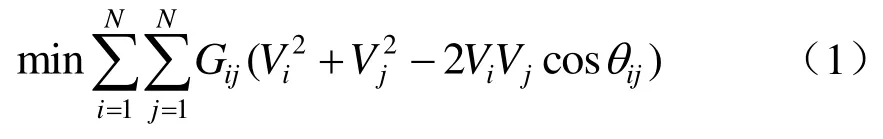
式中：Vi、Vj分别表示节点i、j的电压值；Gij为支路ij的电导；θij为i、j两节点的电压相角差。

2.2 约束条件

2.2.1 潮流约束

供电系统安全运行应满足以下潮流方程[5]：

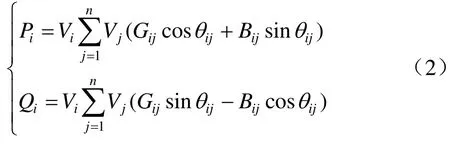
式中：Pi表示35 kV母线上的有功负荷；Qi表示35 kV母线上的无功功率；Gij、Bij分别表示i、j两节点间的电导和电纳。

2.2.2 系统安全运行约束

电压和线路电流满足：

式中：Vi.max、Vi.min分别表示节点i的电压最大和最小幅值；Iij.max为最大载流量。

2.2.3 主变压器有载调压档位约束

式中：Tmax、Tmin分别表示主变压器有载调压抽头的最高档位和最低档位。

3 求解方法

粒子群算法（Particle Swarm Optimization，PSO）算法[6]中群体的每个粒子均为问题的一个可能解，且均与相应适应度值一一对应，PSO算法中的适应度函数与优化问题的目标函数相关，其决定了算法中各个粒子位置的优劣。现记第i个粒子迄今为止搜索到的最优位置为Xp= (xpi1,xpi2, …,xpiN)，其对应的适应度值为pbesti，则整个群体搜索的最优位置为Xg= (xgi1,xgi2, …,xgiN)，其对应的适应度值为gbesti，在每次迭代过程中，粒子通过式（6）和式（7）更新自身的速度和位置。

式中：ω为惯性权重；d= 1,2,…,N；N为搜索空间维数；k为迭代次数；c1和c2为加速度因子；r1和r2为[0,1]范围内的随机数。

PSO算法的初始种群是随机的，不能保证粒子的质量，容易使算法过早收敛陷入局部最优解。本文利用混沌优化方法对粒子群算法进行改进[7]。构成混沌空间的方法中，Logistic混沌映射是典型方法之一，其混沌映射和迭代式分别见式（8）、式（9）。同时，在求解过程中，为了防止粒子陷入早熟问题，算法中设置当适应度方差小于给定方差时，随机产生一个新的起始点对种群进行混沌初始化，使其跳出局部最优解。适应度方差见式（10）。

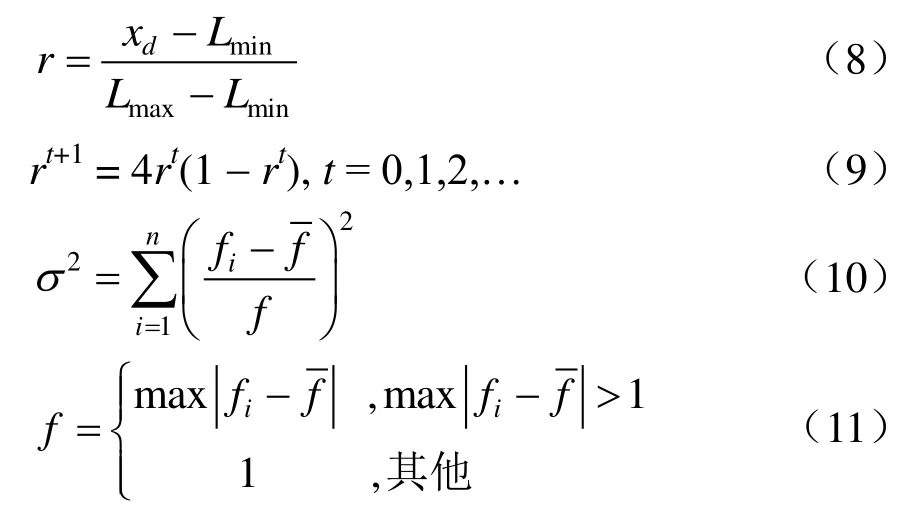
式中：fi为粒子i的适应度值；为当前粒子种群的平均适应度值；f为归一化因子；Lmax和Lmin为控制变量上下限。

混沌粒子群算法（Chaos Particle Swarm Optimization，CPSO）的具体计算流程如下：

（1）算法参数设置并初始化种群。

（2）根据式（6）和式（7）更新粒子速度和位置。

（3）Logistic混沌映射，具体步骤：

a.根据式（8）对迄今为止搜索到的最优位置xd进行混沌映射，得到混沌初始位置矢量r1。

b.根据式（9）的混沌迭代公式进行M次迭代，产生一组混沌序列R= (r1,r2, …,rM)。

c.根据式（8）再对R进行混沌逆映射，得到混沌化后的可行解序列Xd= (xd1,xd2, …,xdM)。

d.计算可行解序列中每个位置对应的适应度函数值，并保留最优值对应的位置，记作。

（5）当适应度方差值小于给定方差值时，当前种群重新进行初始化，返回步骤（2）。

（6）判断是否满足迭代次数，若不满足，则回到步骤（2）继续运算。

4 优化方案

根据已建立的轨道交通交流供电系统优化运行模型和求解方法，供电系统优化方案按照图3所示流程执行。

图3 优化方案流程

5 算例分析

5.1 算例概述

以南宁轨道交通3号线供电系统为例进行验证，基准容量选择100 MV·A，选择在空调季节和非空调季节进行仿真计算分析，进一步分析供电系统的电压质量和线路损耗情况。南宁轨道交通3号线35 kV环网电缆均采用型号为FZ/FYS-WDZA- YJY63-26/35kV的单芯电缆。

通过分析动力变压器的典型负荷曲线可以看出，00：00—00：30和04：30—05：00为车站开启区间早晚通风时段，负荷有短时上升，06：00—23：59为运营时段，负荷较为稳定。运营期间，车站整流变压器由于列车进出站启动制动较为频繁，负荷波动性较大，但全天波动区间较为密集且瞬时性强，故采用其平均负荷表示运营期间的负荷情况。

算例所采用的混沌粒子群优化算法的相关参数设置如下：优化计算的迭代次数为50，粒子群的规模设置为50，加速度因子c1、c2的值分别为1、2，惯性权重ω= 0.5，初始化后的种群在混沌映射后进行不断迭代。算例中主变压器有载调压档位可上下调节10档，且设初始档位状态为基准35 kV处的1档。

5.2 结果分析

记每年5月1日—11月5日为空调季节，每年1月1日—4月30日和11月6日—12月31日为非空调季节，每日区间早晚通风阶段合计1 h。通过在每日运营开始前后和早晚通风阶段前后3个时间段（00：00—00：30，04：30—05：00，06：00—23：59）采用CPSO算法对优化模型求解，得出主变压器的有载调压档位为6档，根据求解结果调整荔园、秀灵主所的主变压器有载调压档位，进而优化全线35 kV环网电压。空调季节、非空调季节优化前后的电压情况分别如图4、图5所示。计算结果分别如表1—表4所示。

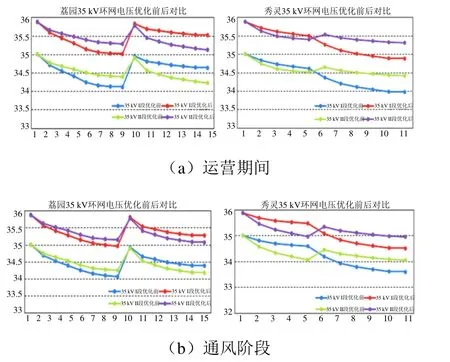
图4 优化前后空调季节下电压幅值对比

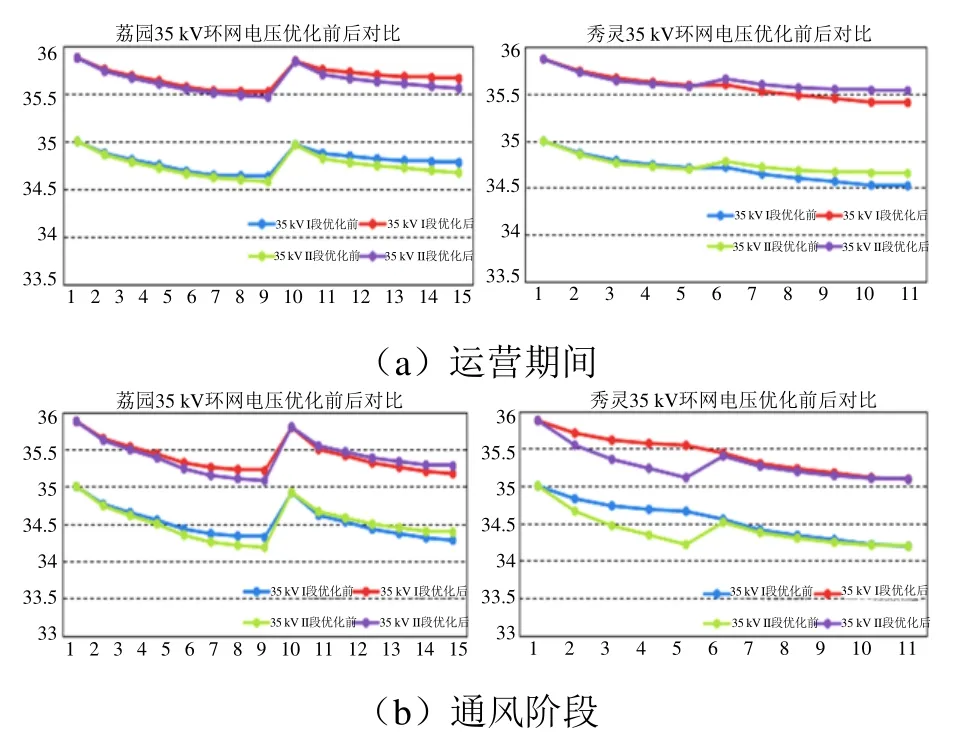
图5 优化前后非空调季节下电压幅值对比

由表1所示运营阶段优化前后荔园和秀灵35 kV Ⅰ、Ⅱ段环网的线路损耗可以看出，优化后的供电系统在全年空调季节的运营阶段可降低电能损耗达15 885.73 kW·h。

表1 空调季节运营阶段优化前后线路损耗 kW

由表2所示区间通风阶段优化前后荔园和秀灵35 kV Ⅰ、Ⅱ段环网的线路损耗可以看出，优化后的供电系统在全年空调季节早晚通风阶段可降低电能损耗804.91 kW·h。

表2 空调季节通风阶段优化前后线路损耗 kW

由表3所示运营阶段优化前后荔园和秀灵35 kV Ⅰ、Ⅱ段环网的线路损耗可以看出，优化后的供电系统在全年非空调季节运营期间可降低电能损耗6 610.66 kW·h。

表3 非空调季节运营阶段优化前后线路损耗 kW

由表4所示区间通风阶段优化前后荔园和秀灵35 kV Ⅰ、Ⅱ段环网的线路损耗可以看出，优化后的供电系统在全年非空调季节通风期间可降低电能损耗502.29 kW·h。

表4 非空调季节通风阶段优化前后线路损耗 kW

根据上述数据分析，南宁轨道交通3号线荔园和秀灵35 kV Ⅰ、Ⅱ段环网线路全年可降低电能损耗23 803.59 kW·h。因此，通过优化35 kV环网电缆的电压质量，可以进一步减少线路损耗。

6 结语

本文以有载调压的档位作为决策变量，将系统线路损耗最小为目标函数，建立城市轨道交通交流供电系统优化模型。同时，采用混沌粒子群算法对优化模型进行求解，通过算例分析验证了该方法可以有效降低供电系统的线路功率损耗，提高运行的经济效益。