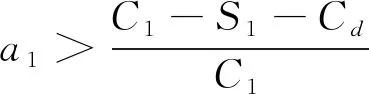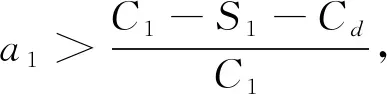政府补贴下建筑废弃物资源化的演化博弈分析

李进涛， 吴 骞

(湖北工业大学土木建筑与环境学院， 湖北 武汉 430068)

随着我国城市化的快速发展，建筑行业发展迅猛，同时也产生了大量的建筑废弃物。据统计，我国建筑废弃物总量约占城市固体废弃物总量的30%～40%[1]。我国建筑废弃物的处理方式主要是填埋和露天堆放，这不仅造成环境污染，而且还浪费资源。建筑废弃物资源化利用可以降低对天然材料的依赖从而有效节约资源、减少污染、刺激经济，是建筑废弃物产生后最有效的处理方式[2]。

在过去的几十年里，研究者从不同的视角对建筑废弃物资源化问题进行了研究。在资源化管理手段方面，有学者指出政策支持对鼓励采取减废措施很重要[3]，如实施建筑废弃物处置收费政策[4]，实施奖惩相结合的政策[5]，将PPP模式引入建筑废弃物处理产业[6]，这些均能有效解决建筑废弃物的管理问题。还有些学者对建筑废弃物资源化的效果进行评估。例如，评估建筑废弃物管理以及不同处置方法的经济和环境效益[7-8]、不同分类系统对环境效益的影响[9]、建筑废弃物移动式资源化处置的环境影响[10]。另外，许多学者还探究了建筑废弃物管理的影响因素，如Osmani和朱姣兰等研究了从业人员建筑废弃物管理行为的影响因素[11-12]，Lu等识别出建筑废弃物有效管理的七个关键成功因素[13]，Hao等指出影响建筑废弃物管理的因素包括法规的完善程度、政府的监管力度和回收市场的成熟度[14]。

上述研究主要关注建筑废弃物资源化行业的外部结构，然而，研究资源化行为决策的内在机制是提高资源化率的重要途径。随着博弈论的发展，演化博弈为研究行为决策提供了一种实用的方法。近几年有学者运用演化博弈来分析建筑废弃物资源化行业利益相关者的行为决策。例如，分析有无公众参与下建筑承包商和政府部门的决策行为[15]，研究政府部门与建筑垃圾生产单位之间的策略选择[1]，探究不同社会监督水平下施工单位与监管部门的演化策略[16]。前人的研究主要集中在政府和单个利益相关者之间的行为决策的影响，忽略了建筑废弃物资源化过程中两个主要的参与主体，即建筑企业和建筑材料制造商之间的合作以及政府干涉对双方合作的影响。鉴于此，本文构建建筑企业与建筑材料制造商之间的博弈模型，探究建筑企业和建筑材料制造商的策略选择，分析在政府补贴下，双方决策行为的演化路径以及政府补贴的合理范围。为了便于分析，本文将废弃物资源化利用企业和建材生产企业抽象为建筑材料制造商。

1 演化博弈模型的构建

对于建筑企业，面临两种策略选择：一是将建筑废物运送至建筑材料制造商作为原材料进行资源化，但此时会产生额外的分类分拣成本；二是直接将建筑废弃物运送至填埋场。对于建筑材料制造商，也面临着两种策略选择：一是选择建筑废弃物作为原材料，对其进行分类、处理，并在工厂中用于生产建筑材料，但此时需要引入先进的设备、技术和人员，因此需要投入额外的成本；二是选择天然原料作为原材料来生产建筑材料。综上所述，建筑企业和建筑材料制造商的策略集合为(参与，不参与)。

基于上述策略，本文做出下列假设：

假设一：博弈双方均为有限理性，他们都能够学习和适应动态环境变化，并在建筑废弃物资源化过程中调整和优化策略。

假设二：当博弈双方选择参与资源化时，建筑废弃物资源化行业运行良好，并带来一定的环境、社会和经济效益F。建筑企业和建筑材料制造商可从F中获得的利益比例分别为α和β。当只有一个或两个利益相关者都不参与资源化时，就不会产生环境、社会和经济效益。

假设三：如果建筑企业选择参与资源化，则额外的分类分拣成本为C1，此时还会得到政府的成本补贴，补贴率为a1。若建筑材料制造商不参与资源化，那么建筑企业的收益为S1；若建筑材料制造商参与资源化，那么建筑企业的收益为S1+αF。相反地，如果建筑企业不参与资源化而将废弃物运至填埋场填埋，则填埋成本为Cd。

假设四：如果建筑材料制造商不参与资源化，则其收益为S2，运营成本为C2。相反地，如果建筑材料制造商参与资源化，且建筑企业也参与资源化，则其收益为S2+βF，但是建筑材料制造商还需要承担引入先进设备、技术和人员所花费的额外成本C3，但此时会得到政府的成本补贴，补贴率为a2。

假设五：选择参与资源化的建筑企业比例为x，选择不参与资源化的建筑企业比例为1-x。选择参与资源化的建筑材料制造商的比例为y，选择不参与资源化的建筑材料制造商的比例为1-y，显然，0 ≤x≤ 1，0 ≤y≤1。

基于上述模型描述与假设，建立了政府补贴下建筑企业和建筑材料制造商之间的收益矩阵，如表1所示。

表1 建筑企业和建筑材料制造商之间的收益矩阵

2 演化博弈模型分析

2.1 复制者动态方程求解

根据表1，可得出建筑企业参与资源化时的期望收益E11，不参与资源化时的期望收益E12以及平均收益E1。计算式如下：

E11=y[S1+αF-(1-a1)C1]+(1-y)[S1-(1-a1)C1]

(1)

E12=y(-Cd)+(1-y)(-Cd)=-Cd

(2)

E1=xE11+(1-x)E12

(3)

根据Malthusian动态方程，由式(1)，(2)，(3)可得建筑企业参与资源化比例下的复制动态方程：

(4)

同理，建筑材料制造商参与资源化比例下的复制动态方程为：

(5)

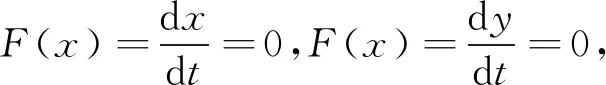
2.2 演化稳定策略分析

利用复制动态方程求出的局部均衡点不一定就是系统的演化稳定策略(ESS)，根据Friedman法，可以通过系统的雅可比矩阵J的局部稳定分析得出系统的演化稳定策略。

只有当矩阵J满足以下两个条件：1)矩阵的行列式大于零(即DetJ>0)；2)矩阵的迹小于零(即TrJ<0)时，该点具有局部稳定性，即为稳定演化策略。

根据方程(4)和(5)，可得该系统的雅可比矩阵为：

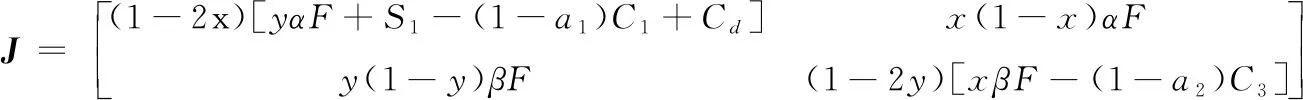
将前面5个均衡点代入到上述矩阵，可求得该系统的DetJ和TrJ如表2所示。

表2 系统均衡点对应的Det J和Tr J

情形一：当S1-(1-a1)C1+Cd<0且αF+S1-(1-a1)C1+Cd<0时，系统相位演化图如图1a和b所示。此时(不参与，不参与)是双方的最终选择。对于建筑企业来说，加上增量收益αF后的净收益小于填埋的净收益，此时建筑企业倾向于不参与资源化；而对于建筑材料制造商来说，由于建筑企业不愿意参与资源化而将产生的建筑废弃物直接运送至填埋场填埋，使得建筑材料制造商缺乏原材料来源，因此无论增量收益βF是否大于政府补贴后的额外成本，此时参与资源化的建筑材料制造商的比例将减少，最终双方无法达成合作的局面。

情形二：当S1-(1-a1)C1+Cd>0且βF>(1-a2)C3时，系统相位演化图如图1c所示。此时(参与，参与)是双方的最终选择。此时，建筑企业参与资源化带来净收益大于填埋的净收益，建筑材料制造商资源化带来的增量收益βF大于政府补贴后的额外成本，双方均有利可图，所以双方均愿意参与资源化。

情形三： 当S1-(1-a1)C1+Cd>0且βF<(1-a2)C3时，系统相位演化图如图1d所示。此时(参与，不参与)是双方的最终选择。此时，建筑企业参与资源化带来的净收益大于填埋的净收益，建筑材料制造商资源化带来的增量收益βF小于政府补贴后的额外成本。所以建筑企业愿意参与资源化，而建筑材料制造商不愿意参与资源化，最后双方无法达成合作。

情形四：当S1-(1-a1)C1+Cd<0，αF+S1-(1-a1)C1+Cd>0且βF<(1-a2)C3时，系统相位演化图如图1e所示。此时(不参与，不参与)是双方的最终选择。对于建筑企业来说，参与资源化后的净收益大于填埋时的净收益，所以建筑企业倾向于参与资源化；对于建筑材料制造商来说，增量收益βF小于政府补贴后的额外成本，所以建筑材料制造商不愿意参与资源化。由于建筑材料制造商不参与资源化，那么建筑企业将被迫无法进行资源化，最后双方无法达成合作。

情形五：当S1-(1-a1)C1+Cd<0，αF+S1-(1-a1)C1+Cd>0且βF>(1-a2)C3时，系统相位演化图如图1f所示。对于建筑企业来说，参与资源化的净收益小于填埋的净收益，但加上增量收益αF后的净收益大于填埋的净收益，所以建筑企业倾向于参与资源化；对于建筑材料制造商来说，增量收益βF大于政府补贴后的额外成本，所以建筑材料制造商也愿意参与资源化。但只要有一方不参与资源化，最终将无法达成合作局面。所以，系统的ESS为(0,0)和(1,1)。

2）相关性关联关系，相关性关联是指同一视图或者不同视图档案特征之间存在的依存、制约、因果等隐含的关系。构建相关性关联关系是指通过分析已有的档案相关关系，基于统计分析寻找档案特征同时出现的规律和模式的过程。两个特征之间的相关关联分析多采用熵与互信息进行度量。对于任意的 f1,f2∈R，I表示(f1,f2)的互信息即I(f1,f2)=，给定阈值δ，当I(f1,f2)＞δ时，认为特征fi,fj之间存在相关关系，即节点vi,vj之间存在相关关联关系。

图 1 系统演化相位图

2.3 参数变化的影响

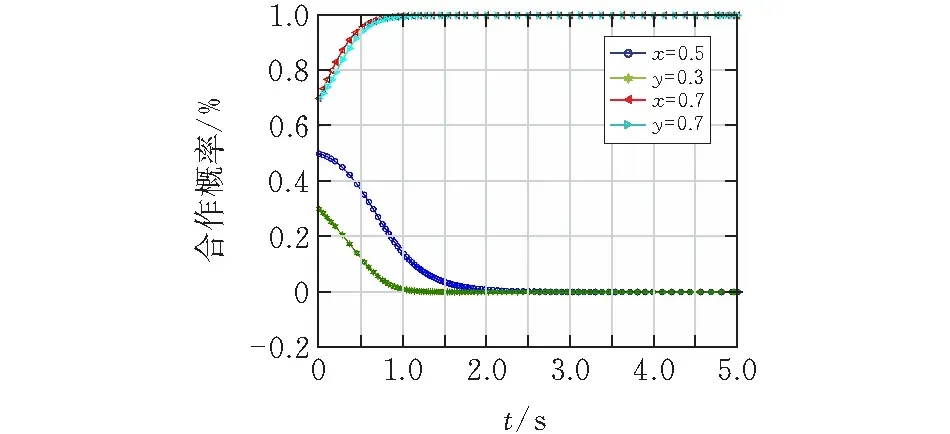
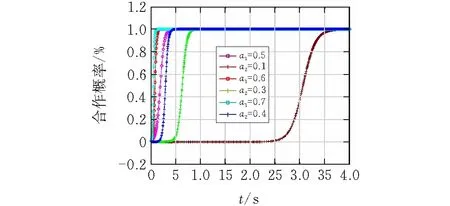
由前面的分析可知，当满足S1-(1-a1)C1+Cd<0，αF+S1-(1-a1)C1+Cd>0且βF>(1-a2)C3时，系统的ESS为(不参与，不参与)和(参与，参与)。由于SOADC和SABCD的面积表示双方是否合作的概率，所以这两个区域的面积大小决定了系统最终演化结果。若SOADC>SABCD，演化结果趋向于(0,0)；若SOADC

由图1f可得SABCD的面积，即(1,1)为演化稳定策略的概率为：

(6)

根据方程(6)，影响系统演化的因素有9个，可以得出进一步的结论，如表3所示。

表3 因素变化对系统演化结果的影响

由表3可得：分类分拣成本为C1、引入先进设备、技术和人员所花费的额外成本C3越高，双方合作的概率减小。建筑企业和建筑材料制造商只要有一方成本过高，双方合作的概率将减小。此时，政府补贴对促进双方合作具有重要意义，当补贴率a1、a2越大，双方合作的概率也将增大。

填埋成本为Cd，资源化效益F，两个利益相关者从F中获得的利益比例α和β，建筑企业的收益S1越大，双方参与资源化的概率越大。对于建筑企业，参与资源化的收益越大、填埋成本越高，建筑企业越倾向于参与资源化，随着建筑企业资源化的比例增加，建筑材料制造商实施资源化的比例也将增加，最终双方达成合作。当资源化带来的效益F越大且双方从F中获得的利益比例α和β越大，双方参与资源化的概率也越大。

3 演化博弈模拟仿真

为了更直观的研究建筑企业和建筑材料制造商之间的演化策略，本节利用MATLAB来模拟参数变化时相应演化博弈策略变化的结果。考虑到篇幅限制以及相关参数的数据获取困难，本文具体参数值的设置满足前述的基本假设。

为了检验情形五中建筑企业和建筑材料制造商是如何在策略(不参与，不参与)和策略(参与，参与)之间进行权衡，此时参数应满足S1-(1-a1)C1+Cd<0，αF+S1-(1-a1)C1+Cd>0且βF>(1-a2)C3。所以，令S1=20，a1=0.2，a2=0.4，C1=35，Cd=5，C3=15，α=0.3，β=0.5，F=30。通过上述参数设置，可计算得x*=0.6，y*=0.33。固定其他参数，通过改变初始策略(x0，y0)来检验演化趋势。由于x*=0.6，y*=0.33，因此，设初始策略(x0，y0)为(0.5，0.3)和(0.7，0.7)。演化趋势如图2所示。

由图2可知，当x0=0.5x*，y0=0.7>y*时，建筑企业参与资源化的比例x和建筑材料制造商参与资源化的比例y均趋向于1，故该系统的稳定演化策略为(参与，参与)，双方达成合作状态。

图 2 情形五的演化趋势

图 3 a1=0，a2=0.1/0.2；a1=0.2，a2=0.1时双方演化趋势图

图 4 a1=0.5，a2=0.1时双方演化趋势图

图 5 a1=0.5，0.6，0.7和a2=0.2，0.3，0.4时双方演化趋势图

4 结论与建议