基于力学模型分析采空巷道顶板安全厚度

文／郭清石、万文涛 江西省交通设计研究院有限责任公司 江西南昌 330052

引言：

随着江西省境内大量的公路的建设，建设用地紧张导致线路无法避免采空区等不良地质段，国内针对采空区路基设计时一般采取桩板结构跨越、注浆充填等措施，实际上部分采空巷道顶部具有一定的承载能力，在采空巷道顶板满足厚度及强度要求时候，采空巷道可不进行处理。为了评价采空巷道在车辆荷载的作用下的稳定性，本文根据岩体力学的理论得出岩体的强度指标，并分析了车辆荷载在采空巷道顶板产生的荷载情况，根据材料力学理论计算出采空巷道在车辆荷载作用下所需的最小顶板厚度。

1、工程概况

1.1 工程简介

该公路为一条一级公路，全线采用双向四车道一级公路标准新建，设计标准如下：设计速度：80km/h;路基宽度：整体式路基：25.5m，其横断面布置为：0.75m（土路肩）+3m（硬路肩）+2×3.75m（行车道）+0.5m （路缘带）+2.0m（中央分隔带）+0.5m（路缘带）+2×3.75m（行车道）+3m(硬路肩)+0.75m(土路肩)。路线于K0+300～K0+700段跨越采空区，据调查该采空区为萤石采矿区，开采时间较早于2009年停产关闭，开采巷道宽度2-3m，埋深不一，地表零星分布有开采巷道的入口。

1.2 工程地质条件

2、基于塌陷理论顶板安全厚度分析

根据塌陷理论：巷道顶板塌陷后，塌落的体积增大，当塌落至一定高度h 时，巷道自行填满，无需考虑对地基的影响。所需塌落高度h 按下式计算：

式中 h—塌落前的洞体高度（m）；

K—岩石松散（胀余）系数，石灰岩取1.2，砂岩取1.1，粘土取1.05。

采空巷道的高度约为2-3m，为工程安全考虑取采空巷道的高度h=3m，岩石松散（胀余）系数K=1.1的根据（1）式，该采空巷道所需的塌陷岩体的厚度 h =30m；该法计算出的采空巷道顶板的最下安全厚度为30m。

采空巷道塌陷理论是一种经验的估算方法，其假定条件为采空巷道的顶部会发生塌陷，未考虑采空巷道顶部本身的自身承载能力，该方法只考虑了采空巷道高度的影响，对宽度的影响未考虑，与实际的采空塌陷破坏模式相差较大，对塌陷发生的过程及影响结果均较粗糙，分析结果安全系数偏高，运用于工程建设会导致较大的浪费。

3、基于岩体强度顶板安全厚度分析

3.1 岩体强度计算分析

岩体强度是评价工程岩体稳定性的重要指标，其强度受岩石强度及岩石完整程度控制，Hoke和Brown（1980）根据岩体性质的理论与实践经验，用试验法导出了岩块和岩体破坏时主应力的关系为：

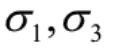
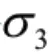
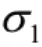
根据（2）、（3）式可解得岩体的单轴抗压强度

岩体的单轴抗拉强度

3.2 采空巷道顶板岩体受力分析

根据图1采空巷道地质模型可将巷道顶板简化为跨越巷道的受力梁来进行力学分析计算。根据现场调查岩体结构面以近于水平状层理面为主，岩体完整程度高，巷道顶板岩体受力可采用两段固接的三次超静定梁，梁的跨度取巷道的最大宽度3m。（图2）

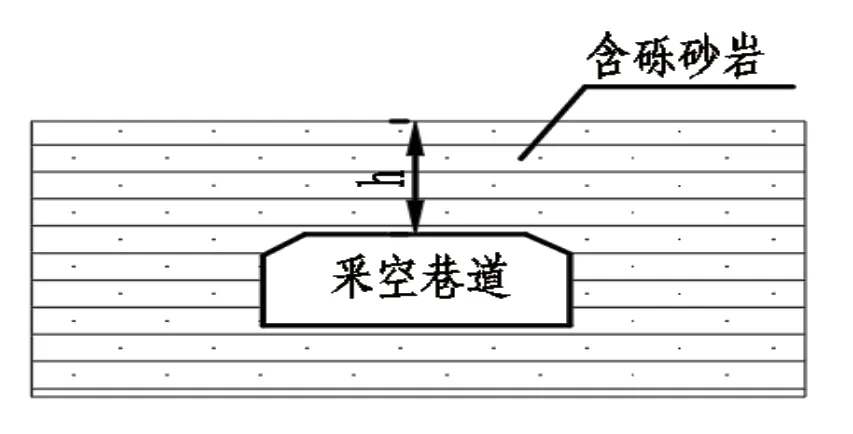
图1 采空巷道地质模型

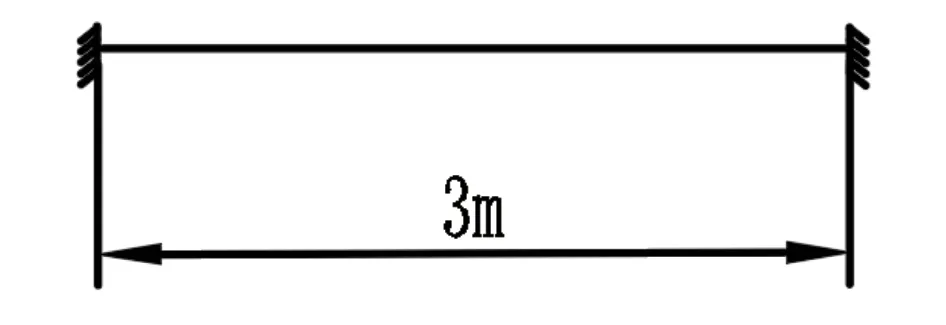
图2 顶板岩体简化的受力梁模型

采空巷道的顶板受承受的应力为岩体自重应力及车辆荷载引起的附加应力的叠加。该公路为一级公路，采用的公路荷载等级为公路-I级荷载，巷道顶板受力荷载采用车辆荷载，车辆荷载布置图如图3：

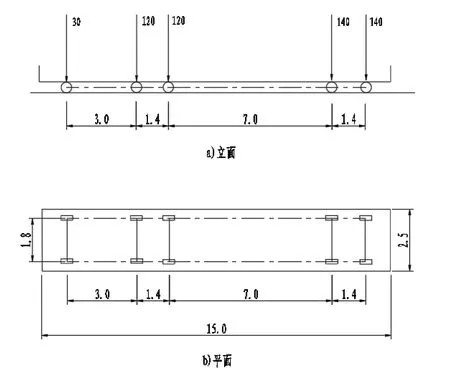
图3 车辆荷载布置图（轴重力单位：KN；尺寸单位：m）

根据荷载布置图巷道顶板岩体所受车辆荷载的最大轴重为后轴重力标准值，巷道顶板岩体为脆性岩石，顶部跨中弯矩为顶部破坏的控制弯矩，根据结构力学分析，顶板岩体受力最不利位置如下图4：

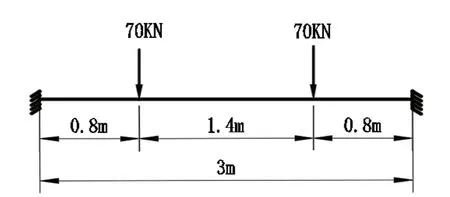
图4 顶部岩体受力最不利位置荷载布置图

上述70KN为车轴的单边车轮荷载。上图最不利位置下顶板岩体的受力弯矩图如下图5：

图5 最不利位置下车辆荷载引起顶板岩体弯矩图

图6 自重应力下顶板岩体受力图

在自重应力荷载的作用下顶板岩体的弯矩图如下图7：

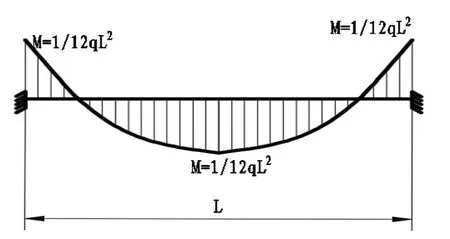
图7 自重应力下顶板岩体弯矩图

根据以上分析在车辆荷载和自重应力荷载作用下顶板岩体的最大弯矩M为跨中弯矩其值如下：

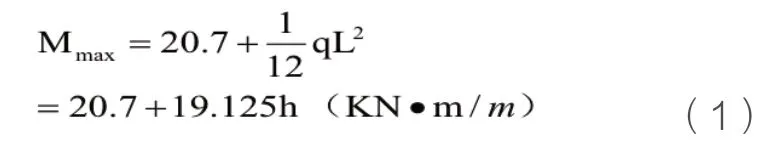
岩体的强度指标已考虑结构面的影响，可作如下假设：岩体为均匀的各向同性的材料，踩空巷道的顶部视为高度为h的半无限长矩形，取单宽b=1m，根据材料力学分析可得单宽岩体弯曲截面系数：

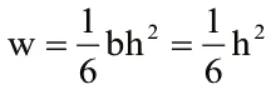
带入（1）式得h＞14.53m；即采空巷道的顶板厚度的临界安全厚度14.53m。

4、安全厚度的综合确定

塌陷理论基于巷道塌陷后的分析计算，该法的假设条件为巷道顶板发生塌陷；基于岩体强度分析出的安全厚度以巷道顶板岩体强度能承受车辆荷载及自重荷载作用下计算出的安全厚度。塌陷理论计算出的安全厚度h=30m大于强度分析计算的安全厚度h=14.53m，即采空巷道顶板厚度h=30m后，岩体不会发生塌陷，故塌陷理论计算出的安全厚度偏保守，实际应用应以强度理论计算出的安全厚度作为依据。

上述两种方法各有其适用性，采空巷道顶板岩石层理面为大倾角的层理面为时，在车辆荷载作用下岩体会沿着层理面等软弱结构面发生塌陷，塌陷理论更具有适用性；采空巷道以小倾角的层理面时，可分别采用强度理论及塌陷理论进行计算，对比确定采空巷道顶板的最小安全厚度。

结语：

本文以某一级公路跨越采空巷道为例，采用塌陷理论及岩体强度理论对采空巷道顶板最小安全厚度进行计算分析得出的结论如下：

（1）采空区中的采空巷道具有一定的承载能力，当采空巷道的顶板安全厚度达到要求后可不进行处理，节约工程造价。

（2）采空区勘察中，加强对岩体结构面的间距、产状测量为计算岩体的强度及选择合适的方法评价最小安全厚度提供依据。

（3）本文采取强度理论计算采空巷道的顶板最小安全厚度是采取规范规定的轴载，实际应用中，可收集通行车辆的最大轴载，用于计算安全厚度。

（4）本文采取力学分析模型为三次超静定梁，根据计算结果梁的跨度与高度比很小，梁的受力模式为深受弯构件受力模式，计算中也可考虑梁端的弯距调幅，但调幅幅度不宜过大。

（5）采空巷道顶板受力包括弯矩、剪力，顶部岩体近于水平状，其竖向抗剪能力较强。其受弯矩控制的顶板安全厚度大于受剪力控制的安全厚度故本文未对剪力控制进行验算。对顶部岩体产状较陡情况，在车辆荷载作用下，易发生沿层理面滑移破坏，力学模型分析法应进行剪力复核验算。

（6）本文将岩体换算为均质材料采用的强度指标为单轴抗压力学指标，实际岩体的受力为三向受力，在围压的作用下岩体的三向抗压指标是大于单轴抗压指标，故本文的计算厚度是偏安全的，故本文在力学模型的分析中未设置安全系数。

（7）塌陷理论及强度理论在安全厚度的计算中各有其适用性，实际使用中可根据采空巷道顶板岩体结构面的强度及产状具体分析确定。