线性代数中初等变换的“不变”与“变”

夏文华，王祝君

（湖南工程学院 计算科学与电子学院，湖南 湘潭 411104）

线性代数是大学数学中的一门重要课程，是工科及经济管理类学生一些后续课程的基础。线性代数中用得最多的是“矩阵的初等变换”。不少学者从不同研究角度探索了初等变换的应用，并就矩阵初等变换的教学进行了一些探讨，［1-7］“矩阵初等变换是线性代数课程中一种重要且基础的运算法则，它是研究矩阵、向量组线性相关性、线性方程组的解、二次型以及线性空间等内容不可替代的工具”［1］。因为用的地方多，而线性代数学时较少，学生对初等变换在使用时会带来的变化不清楚，或者不清楚在不同地方使用初等变换的条件，从而导致学生在学习时常常容易糊涂，思维混乱，综合做题时错误百出。本文从初等变换“不变”与“变”的角度来理顺线性代数课程的学习思路。

一 初等变换不改变矩阵的秩

定理1：［8］68若A～B，则R(A)=R(B)。

即：初等变换不改变矩阵的秩。

定理2：［8］93矩阵的秩等于它的列向量组的秩，也等于它的行向量组的秩。

根据以上定理我们可以解决以下两个问题：

（1）求矩阵的秩；（2）求向量组的秩。

如果只求矩阵或向量组的秩，一般学生都没有问题，向量组无论是以行的形式，还是列的形式作成矩阵都可以。但是在求向量组的极大无关组时，学生就会开始犯错，主要错误就是将向量组作为矩阵的行向量组，但是实施的却是初等行变换，这样得到的该向量组的秩还是不变，但是极大无关组却变了。

例1.给出向量组：

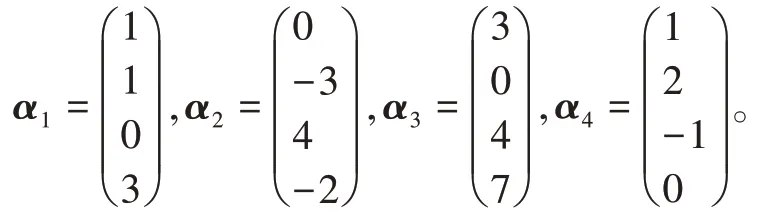
我们将该向量组作为矩阵的列向量组，并对其实施初等行变换将其化为行阶梯形矩阵：

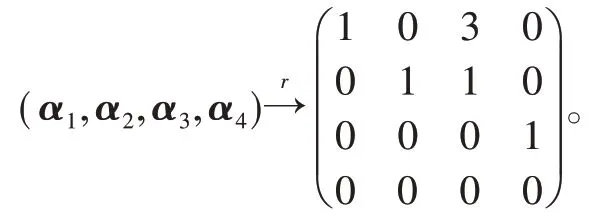
得秩为3，极大无关组为α1,α2,α4。

若将该向量组作为矩阵的行向量组，仍然对其实施初等行变换化为行阶梯形：

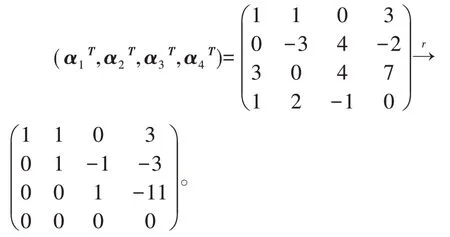
也能得秩为3，但是不少学生还将行向量组看成和列向量组一样从而得出错误结论：极大无关组为α1,α2,α3.事实上α1,α2,α3是线性相关的。

学生往往只记得初等变换不改变矩阵的秩，且矩阵行向量组的秩＝矩阵列向量组的秩＝矩阵的秩，但却忽略了极大无关组的定义，从而错误地将矩阵列向量组的极大无关组与行向量组的极大无关组混淆了。

故而在教学时需要强调：（1）如果求向量组的秩，无论是以列的形式还是以行的形式作成一个矩阵都可以，无论用行变换还是用列变换也都可以，这就是“不变”；（2）如果求向量组的极大无关组，就要注意向量组的摆放形式，摆放形式不同，初等变换方式也不同，这就是“变”。且：（1）若以列的形式作成矩阵，则做初等行变换将矩阵化为行阶梯形，那么行阶梯形矩阵的每一行首非零元所在列对应的原向量即为极大无关组；（2）若以行的形式作成矩阵，则做初等列变换将矩阵化为列阶梯形，那么列阶梯形矩阵的每一列首非零元所在行对应的原向量即为极大无关组。

如例1 中的向量组α1,α2,α3,α4，若将该向量组以列的形式作成矩阵，则只实施初等行变换：

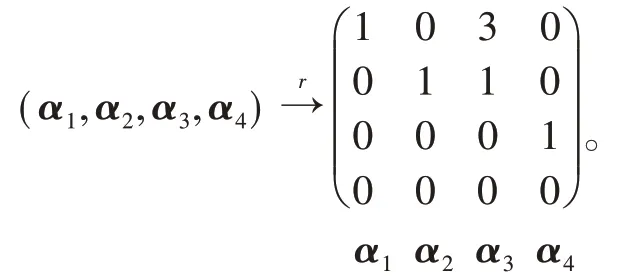
得极大无关组为α1,α2,α4，且α3= 3α1+α2+ 0α4。

若将该向量组以行的形式作成矩阵，则只实施初等列变换：

由此可知，不管是行向量组还是列向量组，为免学生混淆出错，可要求学生都将向量组作成矩阵的列向量组，只实施初等行变换，所得结论不变。

二 初等行变换不改变线性方程组的解

线性方程组与其增广矩阵是一一对应的，对线性方程组的增广矩阵做初等行变换所得矩阵所对应的方程组与原方程组同解。也就是说初等行变换不改变线性方程组的解。

由此，可以利用初等行变换来解决以下三个问题：

1.求解线性方程组Ax=b，其中

A中的第i列αi即为xi的系数，B中的第i行对应的是第i个方程的系数和常数项。根据增广矩阵的意义和解方程组的习惯一般只能做行变换。如果将增广矩阵转置则就只能做列变换，方法同例1 中用初等列变换求行向量组的极大无关组。但是，因为这种方式不符合我们通常写方程组的习惯，所以我们强调在解线性方程组时，对其增广矩阵只实施初等行变换。那么，凡是需要求解线性方程组时，我们都只强调做初等行变换，一般不允许做初等列变换。

2.判断向量组α1,α2,…,αn的线性相关性。向量组α1,α2,…,αn线性相关⇔以该向量组为系数矩阵的齐次线性方程组Ax= 0 有非零解⇔R(A)＜n（n为向量的个数）；向量组α1,α2,…,αn线性无关⇔以该向量组为系数矩阵的齐次线性方程组Ax= 0 只有零解⇔R(A)=n（n为向量的个数）。

那么，可以提醒学生注意：若只判断向量组是否线性相关，行列变换都可以；若在向量组线性相关时还要求求出具体表达式，则须将该向量组作为矩阵A的列向量组且只能做初等行变换。

3. 判断一个向量b是否能由一个向量组α1,α2,…,αn线 性 表 示。 向 量b能 由一个 向量 组α1,α2,…,αn线性表示⇔以该向量组为系数矩阵A，以b为常数列的非齐次线性方程组Ax=b有解⇔R(A)=R(B)；向量b不能由一个向量组α1,α2,…,αn线性表示⇔以该向量组为系数矩阵A，以b为常数列的非齐次线性方程组Ax=b无解⇔R(A)≠R(B)。

可以提醒学生注意：所有向量均作为矩阵A和B（B=(α1,α2,…,αn,b)）的列向量组，且只能做初等行变换。

总之，凡是牵涉到线性方程组的求解，所有向量均做成矩阵的列向量组，且只做初等行变换。

三 相似变换不改变矩阵的特征值

按照矩阵特征值与特征向量的定义，一般线性代数的教材都是根据 |A-λE|= 0 来求矩阵的特征值，再通过解齐次方程组(A-λE)x= 0 基础解系的方式来求对应特征向量。

显然，三角阵或对角阵的特征值就是主对角线上的元素。而对矩阵A可以作初等变换将其化为三角阵或对角阵。所以，很多学生会因为前段时间学习的惯性，自然想到将矩阵通过初等变换化为三角阵或对角阵以此来得出矩阵的特征值。但是，一般对矩阵A作初等变换所得矩阵与A的特征值是不相同的。也就是说对矩阵做初等变换会改变它的特征值。

如果对矩阵A作初等变换，则：

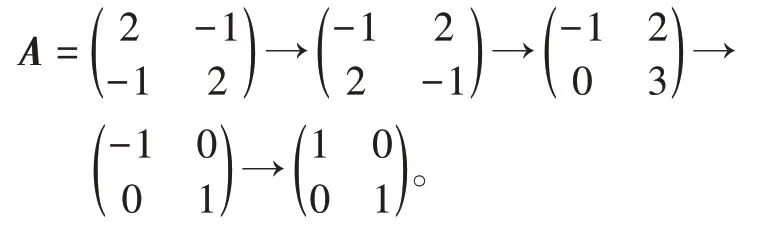
显然，不能由A经初等变换所得的三角阵或对角阵得出A的特征值。事实上，由(λ- 1)(λ- 3)=0，得A的特征值：1,3。

然而，有一种特殊的初等变换不改变矩阵的特征值，这就是相似变换。

定义 1：［8］124设A，B都是n阶矩阵，若有可逆矩阵P，使得P-1AP=B，则称A与B相似。

定理 3：［8］124若n阶矩阵A与B相似，则A与B特征值相同。

根据定义1 和定理3，可知：如果能找到一个可逆矩阵P，使得A与一个上（下）三角阵B相似，那么A的特征值等于三角阵B的特征值，也即为B的对角线上的元；如果能找到一个可逆矩阵P，使得A与一个对角阵Λ相似，那么不仅可以根据Λ主对角线上的元得出A的特征值，还可以求出对应特征值的特征向量。

这种方法教材中很少介绍。这里给出具体方法如下：

由相似的定义，A与Λ相似⇔存在可逆矩阵P，使得P-1AP=Λ。

而可逆矩阵P可以表示成一系列初等矩阵的乘积 ，即P=p1p2…pl，那 么P-1=pl-1…p2-1p1-1，则P-1AP=Λ⇔pl-1…p2-1p1-1Ap1p2…pl=Λ。 即 ：对A实施一次初等行变换（左乘pi-1），就对A再实施一次相应的逆的初等列变换（右乘pi），这样“成套”地对A作初等变换，直到将A化为对角阵Λ，那么P=p1p2…pl，而Ep1p2…pl=EP=P。

于是，我们将A与一个与之同阶的单位矩阵E作成矩阵按照以上方法进行初等变换，列变换对A与E同时进行，行变换只对A实施。将化为则由Λ可得A的特征值，而P的列向量组则是对应特征值的特征向量。

为方便描述，我们给出以下定义：

定义2：如果对A实施一次初等行变换（左乘pi

-1），就对A再实施一次相应的逆的初等列变换（右乘pi），这种“成套”地对A作初等变换的方法，称为“成套”初等变换法。

所谓实施一次初等行变换，就实施一次相应的逆的初等列变换的意思是：

若对A实施一次互换第i行与第j行的变换（ri↔rj），就对A再实施一次互换第i列与第j列的变换（ci↔cj）；

若对A实施一次将第i行乘k倍的变换（kri），就对A再实施一次将第i列乘倍的变换

若对A实施一次将第i行的k倍加到第j行的变换（rj+kri），就对A再实施一次将第j列的 -k倍加到第i列的变换（ci-kcj）。

如例2，我们采用“成套”初等变换法来求特征值和特征向量：

得A的特征值为：3,1，对应的特征向量分别为

总之，一般的初等变换会改变矩阵的特征值，但因为相似变换不改变矩阵的特征值，所以我们可以利用一种特殊的初等变换——“成套”初等变换法，求出一些矩阵的特征值和特征向量。这种方法具有一定的创新性，可以用来开阔学生思维，更好地理解相似变换。但是，这种方法也具有局限性，不是所有的矩阵都可以用“成套”初等变换法来求特征值，比如不能对角化的矩阵就不能用“成套”初等变换法来求特征值。

四 结语

本文对线性代数中需要用到初等变换的几个地方进行了“不变”与“变”的分析，从初等变换是否改变要求量的角度阐明了初等变换使用的方式和注意要点。学生在学习时不仅需要知道哪些地方需要用到初等变换，还需要清楚知道该用行变换还是列变换，是行列变换都可以，还是行列变换都不可以，只有清楚使用初等变换的方式，才真正弄懂了线性代数这门课程的内涵。从前面的分析我们看到，除了“成套”初等变换法求特征值这一条比较特别之外，解决其他问题时行列变换其实都是可以进行的，但是要注意使用方式，所以在实际教学时，我们可以要求学生一般情况都只用行变换，这样可以有效避免发生错误。当学生熟练掌握了初等行变换和相应理论知识点之后，再引导学生发散思考：如果做列变换是否改变结果，为什么？要怎样做才是正确的？通过全盘提问和最后的总结更有利于学生主动思考问题和理解知识点，提升学生的数学思维能力、创新能力和自主学习能力，最终达到知识融会贯通的目的。