顺水沉放条件下护底软体排排头漂移距水槽试验研究*

杨涵苑，周成洋，夏志康，左利钦，黄廷杰，陆永军

(1.南京水利科学研究院，水文水资源与水利工程科学国家重点实验室，长江保护与绿色发展研究院，江苏 南京 210029；2.武汉大学，水资源与水电工程科学国家重点实验室，湖北 武汉 430072；3.江苏省淮沭新河管理处，江苏 淮安 223001)

软体排是由土工织物系结压载物制成的柔性防冲结构，其整体性高、灵活性好、耐久性强，能自动调节自身形态以适应河床变形，克服了传统防护结构中的诸多问题[1-2]。受不同地区石料运输成本、施工效率、工程造价等因素影响，近年来航道整治工程中多采用软体排作为护滩(底)建筑物[3-5]。由于软体排排垫具有隔离和反滤功能，可大幅削减近岸水流的冲击能量、防止局部淘刷及渗透作用对河床造成变形破坏，并保护排体下方土颗粒不随水流冲刷下移[6-7]。此外，排垫表面的粗糙、多孔性为水生生物及植被生长提供了良好的栖息场所，使其对海洋及河流水文环境的负面影响非常有限。因此软体排在长江[8-9]、密西西比河[10]等大江大河的航道整治工程中发挥着重要作用，取得了良好的洲滩守护效果。

现有软体排的铺排方式可分为顺水流、逆水流及垂直水流沉排。在护滩(底)带中地形平缓的开阔水域往往采用顺水和逆水沉排；而对于受地形影响较大的边滩守护工程，一般由岸边向江心垂直水流铺设。逆水沉排时排体在水中往往发生剧烈震荡或漂浮，存在巨大安全隐患，故很少采用。新型顺水沉排相比垂直水流工艺能有效减小河床底部的溯源侵蚀，因此近些年受到了更多关注。然而，由于迎水面积大、水流顶冲导致排体受力大幅提升[11]。前人针对软体排力学特性、结构设计及铺设工艺等开展了一些研究。朱宪武[12]最早采用悬链线理论对软体排力学特性及水下构型开展研究，推导了排体在静水中的受力计算方法。孙峙华[13]基于集中质量法开发了顺水沉排力学计算模型DASMDS，克服了排体质量不均匀分布及排布拉伸变形问题。张景明[14]根据长江口深水航道治理工程的沉排经验，阐述了软体排的结构形式、设计方法及应用前景。胡利文等[15]针对大榭港区围堤工程实际施工特点，提出了不同水位区域及潮间带的铺排工艺优化方案。杨再常[16]基于排头着床受力分析提出双排头施工技术，大幅增强了顺水沉排时排头锚固作用，有效减少了撕排及断排现象发生。然而，从提高排头着床精度出发，对多因素作用下顺水沉排排头漂移距的变化规律及预测尚缺乏理论与试验研究，导致排头梁、连接绳等设计参数大多依赖经验性判断。

相较于抛石漂移距研究[17]，沉排过程中受排体内部张力作用，导致排头着床区别于抛石沉降的一般性规律。鉴于此，本文通过水槽试验，致力于揭示排头梁质量、连接绳长、水深及流速4个沉排参数对排头漂移距的影响规律，并基于多元非线性回归理论建立排头漂移距预测模型，实现沉排参数与排头漂移距的定量表征，以期为软体排沉排施工及排头精准着床提供理论指导。

1 水槽试验概况

1.1 试验设计

图1a)为铺排船及船载设备进行顺水沉排的实际情景，沉排前预先将混凝土联锁块吊装至甲板指定位置，利用丙纶绳系结于下方排垫。松开卡排梁及卷排筒，使得排头梁牵拉排头沿船舷及翻板下滑并着床。随后沉排船沿水流方向往下游移动一定距离，待联锁块绑扎完成后继续放排并移船，重复沉排操作。本研究根据现场沉排的主要特点，开展软体排沉排的概化水槽试验。试验在南京水利科学研究院铁心桥试验基地泥沙基本理论试验厅的变坡水槽中进行，试验水槽长40 m、宽0.8 m、深0.8 m。水流由泵房从地下水库抽水至过流堰，配合长50 cm的PVC管群进行消能，使得流态沿水槽宽度方向趋于平顺。通过调整电动执行器的开度大小控制水槽入口流量，采用超声波流量计进行测量。

图1 试验设计

原型排混凝土压载块密度为2.35 t/m3，一般选用密度较为接近的铝合金(密度为2.7 t/m3)作为模型材料[18]，将压载块外形概化为圆柱体。根据重力相似原理将排体按1:20比尺进行缩尺制作，计算得到单片铝块直径为16 mm，高为5 mm，质量偏差为1.5%，符合TS/T 231-8—2018《内河航道整治建筑物模拟技术规程》要求(±5%)。由于无法严格按照原型排体构造进行模拟加工，将压载块与排垫的系结方式简化为：采用502胶将铝块按几何比尺等间距粘贴于棉布上的预设位置。试验表明，采用粘接的简化方式并不会改变实际系结方式的排体变形特点。由于软体排在顺水流沉放时所受水流冲击力大，因此实际工程中需在排头处等间距系结混凝土排头梁，用于牵拉排头着床，并锚固于河床底部。如长江下游江乌河段航道整治工程所采用的排头梁质量为770 kg/根，由重力相似计算得到模型梁质量为0.10 kg。本研究选用12 cm宽模型排体(面密度ρs=4.34 kg/m2)，采用强度及耐磨性较好的尼龙绳系结与排体等宽的条形混凝土块开展顺水沉排水槽试验。

1.2 试验工况

本研究设计了5种排头梁质量(0.06、0.08、0.10、0.12、0.14 kg)和连接绳长l(0、0.02、0.04、0.06、0.08 m)、4种水深h和流速v等共计57组试验工况，见表1。其中R1～R25工况旨在探究排头梁及连接绳长对漂移距的影响规律，R26～R41工况主要关注不同水流条件下漂移距的变化特征，R42～R57用于验证漂移距计算模型的预测精度。试验通过卷筒进行放排，待排头梁达到锚固于槽底、不随水流漂移的稳定状态后，采用相机拍摄记录每组工况下排头漂移状态，并将照片导入AutoCAD中测量排头梁着床点距离沉排点的水平距离与水位高度的相对大小，再乘以试验水深得到实际漂移距。为确保试验结果的准确性，每组工况重复沉排3次并对测量结果进行算术平均处理。各典型工况下排头漂移情况见图2。

表1 水槽试验工况

图2 典型工况沉排照片

2 结果与讨论

2.1 漂移距影响因素

图3给出了不同排头梁质量m、连接绳长l工况下排头漂移距s测量结果。由图3a)可知，随着排头梁质量m增大，漂移距s呈幂函数递减。当m由0.53 kg/m增加至1.13 kg/m，l=0 m时，即排头梁直接绑系于排头，s由0.27 m减小至0.14 m，减幅达47.9%；l=0.32 m时，s由0.15 m减小至0.09 m，减幅达44.3%。原因是排体在水下主要受动水压力、排体自重及水上排体牵拉力作用，排头梁的加重减小了软体排自重与动水压力合力的垂向夹角，使得排头梁着床后的平衡状态下，漂移距随排头梁质量的增大而减小。

由图3b)可知，漂移距s随连接绳长l的增大呈指数型递减。当l由0 m增加至0.08 m，对于m=0.53、0.67、0.85、0.96及1.13 kg/m的5组排头梁质量，s减幅分别为43.9%、50.8%、39.9%、45.0%及39.9%。分析认为，产生这一现象的原因是：绳长增加使得排头梁着床时排体入水深度及其在水流方向的投影面积缩小，从而减弱了动水压力对排体的冲击作用。因此，在实际工程中对于沉排较难的施工环境，可适当增大排头梁的连接绳长，但绳长过大可能导致排头缺乏足够牵拉力而在床面附近漂浮震荡。

图3 不同排头梁质量及连接绳长对排头漂移距影响

图4给出了不同水深、流速工况下排头漂移距测量结果。可以看出，随着水深、流速增加，排头所受动水压力增大，使得漂移距s急剧上升。当h=0.15 m，v由0.15 m/s增大至0.3 m/s时，漂移距s由0.05 m增加至0.23 m，增幅达428.7%，此时排头尚处于稳定状态。结合图2可知，排头梁稳定着床时，水下排体近似呈规则的抛物线型。当h=0.2 m，v逐步增大直至超过某一临界值(0.25～0.30 m/s之间)，排体周围流场趋于紊乱，其构型转变为上下起伏的不规则形态。例如R33工况下(v=0.30 m/s)，排头剧烈震荡，反复漂浮、下沉，极难沉排(见图2)。通过不断增加放排长度，最终排头梁在距离沉排点0.42 m位置着床，然而排头梁受水体紊动影响，缺乏足够锚固力以维持排体稳定性。保持流速不变，当h增大至0.25 m以上，强动力作用导致排体呈现与R33工况相似的水下构型，由于水体的剧烈紊动，在排体背水面失稳形成漩涡产生巨大的负压，导致排体所受上举力大于自重，使得排头无法沉降并着床，从而造成沉排失败。

图4 不同水深及流速对排头漂移距影响

2.2 多元非线性回归分析

回归分析是指通过非随机变量估测某一随机变量所进行的数学模型构建及统计分析。一般遵循以下步骤：基于已有数据确定各变量之间的定量关系(回归方程)；检验回归方程的显著性及拟合度；分析自变量贡献值，对各影响因素敏感性进行排序；利用回归方程对某一过程进行预测和控制[19-20]。根据前文分析可知，排头梁质量、连接绳长、水深、流速与排头漂移距呈非线性关系。为建立其预测模型，考虑选用幂指数函数构建3种函数表达式，基于最小二乘法对多因素作用下排头漂移距进行回归分析，得到不同函数形式下回归参数、拟合优度R2、P值等评价指标，见表2。需要说明的是，理论上应采用R1～R41的全部工况作为回归分析的样本数据，但由于R33、R37及R41工况下排体剧烈震荡、浮动，沉排施工具有极大的安全隐患，可能造成浮排、撕排、断排及锚机损坏等事故，甚至危及沉排船安全。因此，上述3种工况的试验结果不纳入样本数据。

表2 多元非线性函数回归分析结果

由表2可知，所构造的3种表达式中，函数1的R2最大，达到0.977，而函数2略小(0.965)。表明上述2种函数的自变量(沉排参数)与因变量(漂移距)存在高度相关性；函数3与函数2均为指数形式，但其放大了指数项中h和v对计算结果的影响程度，使得R2仅为0.128，表明该函数结构无法反映自变量及因变量的相关关系。函数1、2的P值分别为2.08×10-26、1.31×10-23(P<0.05即表示该项显著)，说明存在真实的回归方程，且函数1相比函数2的检验结果更显著。因此，本研究基于多元非线性回归分析确定排头漂移距预测模型如下：

(1)

式中：s为排头漂移距(m)；h为水深(m)；v为流速(m/s)；m为单宽软体排对应的排头梁质量(kg)；l为连接绳长(m)；ρs为排体面密度(kg/m2)。

表3为式(1)中回归参数检验及95%置信度参数区间估计结果。定义l/h为相对绳长，可见，m、l/h、h及v的回归参数的P值远小于显著性水平0.05，表明其与排头漂移距s密切相关。上述因素敏感性排序从大到小依次为v>l/h>h>m，结合参数值的正负可知，v、h对s的作用为显著正相关，而m、l/h为显著负相关。表明在排头漂移距的预测中需首要考虑沉排水域的流速范围，排头梁质量相比无量纲绳长及水深对漂移距的影响较小。此外，各回归参数的置信区间分别为v(1.26，1.52)、h(1.88，2.20)、m(-0.80，-0.61)、l/h(-1.99，-1.61)，可见其区间范围较窄，各因素对漂移距的计算均不可或缺，说明4个沉排参数的显著性较高。

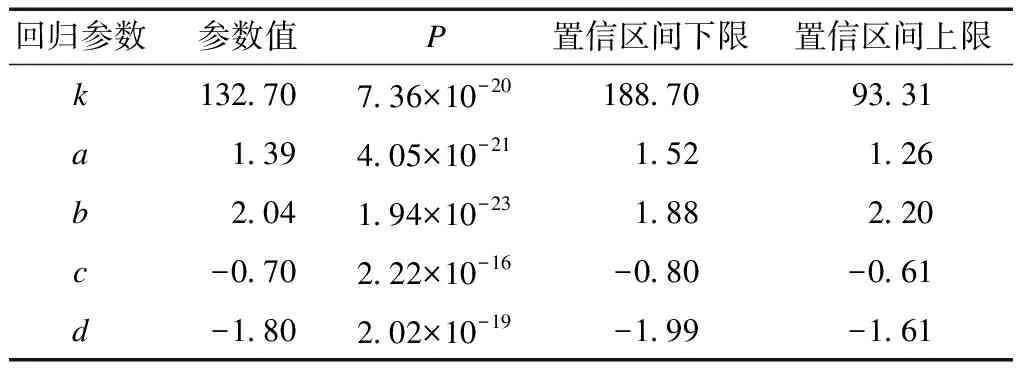
表3 回归参数检验及区间估计结果

2.3 预测模型精度校核

为验证预测模型的准确性，将R42～R57预测样本的试验参数代入式(1)计算，并与试验结果进行线性拟合。引入统计学指标相关系数R、平均绝对百分比误差MAPE及均方根误差RMSE对排头漂移距的拟合结果进行量化分析。MAPE通过逐项比较相对误差，可反映预测值相较计算值的离散程度，RMSE用于衡量预测值的偏差大小，其值越小，预测精度越高。可见，模型计算值与实测值较均匀贴合于y=x线两侧，二者具有良好的相关性(图5)。经计算得到R、MAPE及RMSE分别为0.98、10.85%及0.02 m，表明预测模型具有较高准确性。

图5 排头漂移距计算值与实测值对比

(2)

(3)

(4)

进一步计算所有样本(除失败组次外)的试验值及预测值的相对误差，并进行统计分析(图6)。由图6可见，不同试验条件下排头漂移距的相对误差近似呈正态分布，最大值为25.13%，最小值为-31.27%，且有64.2%的数据集中于-5%～10%之间。可以认为，采用本研究提出的回归模型能较好地预测顺水沉排的排头漂移距，对排头着床位置的精准控制具有重要参考价值。

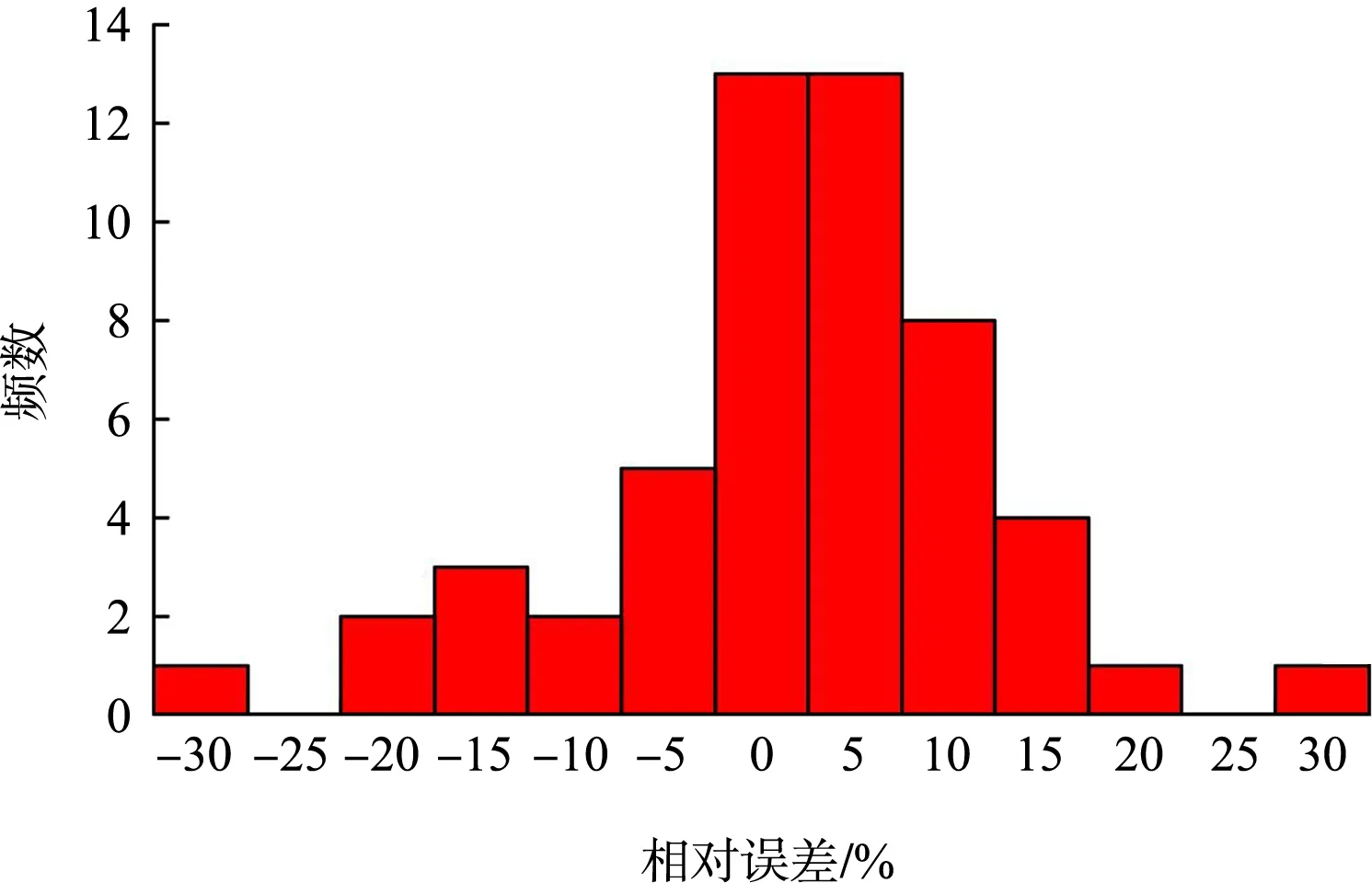
图6 预测模型相对误差统计分析

3 结语

1)排头漂移距与排头梁质量、连接绳长呈非线性负相关；与水深、流速呈非线性正相关。当水流条件达到某一临界值后，排体构型由抛物线转变为上下起伏的不规则形态。

2)沉排参数敏感性从大到小依次为流速>相对绳长>水深>排头梁质量。实际施工时应首要考虑沉排区域的水动力特征，防止由于水体剧烈紊动造成浮排、撕排及锚机损坏等事故发生。

3)本研究建立的预测模型精度较高且形式简洁，相关系数R、平均绝对百分比误差MAPE及均方根误差RMSE分别为0.98、10.85%及0.02 m，表明该回归方程可以较准确计算水槽试验的排头着床位置。如应用于实际工程，还需要更多的室内试验和原型观测数据予以验证。

致谢：本文在试验与写作过程中，与长江南京航道工程局朱文博同志进行了多次讨论，特此致谢。