基于SVR的江苏省交通运输业碳排放达峰预测

王慧茹，封学军，沈金星，张 艳，王海鹏

（1.河海大学 港航物流与绿色发展研究所，江苏 南京 210098;2.河海大学 土木与交通学院, 江苏 南京 210098）

0 引言

当前气候变化是一个全球性的环境问题，它在引起环境变化的同时，也影响着社会各个领域，甚至危及人类生存与发展[1]。联合国政府间气候变化专门委员会（IPCC）第五次气候变化评估报告称，如果不立即采取有效的减缓政策和行动，至2100年，全球平均表面温度相对工业化前将升高3.7 ～ 4.8 ℃，海平面将上升0.6 ～ 0.8 m，造成不可逆转的全球性生态灾难和巨大经济损失。 作为世界上最大的碳排放国，我国“2030年前实现碳达峰，2060年前实现碳中和” 的发展目标引起了世界各国的广泛关注。 交通运输业作为IPCC 确定的第三大碳排放源，在我国占排放总量的10%左右[2]，行业减排对实现碳达峰具有重要意义。 而江苏省工业化程度高、交通便利，应当积极响应国家战略，科学预测交通运输业的碳达峰情况，并制定减排措施和可行的达峰路径。

目前，碳排放研究主要聚焦于碳排放的影响因素分析和量值预测2 个方面。 影响因素分析的主要研究方法包括：改进的Laspeyres 指数法、算术平均迪氏指数分解法（AMDI）、对数平均迪氏指数分解法（LMDI） 和广义迪氏指数分解法 （GDIM） 等。SHIPPER L 等[3]采用改进Laspeyres 指数法对1973年～1992年10 个工业化国家的货运活动和能源使用的碳排放进行分解，认为经济发展水平是影响碳排放最主要的因素；GREENING L A 等[4]利用AMDI法分析1971年～1993年10 个经济合作组织国家的货运碳排放量，认为货运结构的转变导致了碳排放增加。 但是ANG B W 等[5]对指数分解法运用的100 多种情形归类分析后提出，改进Laspeyres 指数法的计算过程在超过3 个因素后将变得复杂，且只适用于加法分解；而AMDI 法具有剩余问题，当数据中存在0 时则无法使用。随着LMDI 法解决了AMDI法和改良Laspeyres 指数法计算的问题，使它们的使用频率降低，更多学者开始采用LMDI 法分析影响因素。国外学者对LMDI 法的应用侧重于国家层面。如TIMILSINA G R 等[6]利用LMDI 法分析了1980年～2005年亚洲国家运输部门的碳排放情况发现，影响中国碳排放增长的主要因素包括人均GDP、人口增长和运输能源强度； 国内学者在侧重国家层面同时，部分学者将研究范围缩小。 如喻洁等[7]将交通运输分为公路、 铁路、 水路和民航4 种方式，基于LMDI 法分析了2005年～2011年碳排放的影响因素，发现人均GDP 为碳排放的主要驱动因素，能源强度和运输强度的降低则起到主要减排效果； 朱桃杏等[8]利用LMDI 法分解2014年～ 2018年各省的物流碳排放发现，由于不同省的经济发展程度和交通基础设施不同，故碳排放存在着明显差异。 随着LMDI 法的广泛应用发现，分解的变量不可以包含多个相对和绝对的因子，且难以反映它们的间接联系。 对此，VANINSKY A[9]提出了一种新的指数分解方法—GDIM，它不仅可包含多个相对和绝对变量，且可准确客观分析变量之间的关系及其对碳排放的贡献。 王勇等[10]应用GDIM 法对东北三省的5 种交通运输方式的碳排放进行分解发现，投资规模是铁路、公路、航空和管道碳排放的主要影响因素，而运输规模则是水路碳排放的主要影响因素。此外，也有学者认为，产业结构[11]和城镇化率[12]也是影响交通碳排放的重要因素。 说明不同地区影响交通碳排放的因素不尽相同，且交通运输的不同部门也有各自的影响因素。

预测碳排放量的模型分为混合构建模式和直接构建模式2 种。 混合构建模式是基于碳排放与宏观经济、能源消费、部门技术等因素之间的关联关系构建投入产出和“可计算一般均衡”（CGE）等模型预测碳排放。 如：王海建[13]基于1987年中国18 个部门（包含交通部门） 的投入产出表预测2020年的能源消费和碳排放量；王灿等[14]基于2000年中国10 个部门（包含交通部门）的数据，应用CGE 模型预测设定情景下2010年各部门的减排贡献。混合构建模式需要大量技术数据，应用困难较大。而直接构建模式是基于碳排放与影响因素的相互关系，构建LEAP模型、Kaya 恒等式和STIRPAT 模型等预测碳排放。如：刘俊伶等[15]通过构建LEAP 模型，在设置3 种不同低碳情景下，预测我国交通部门将于2030年左右碳达峰；王海林等[16]利用Kaya 恒等式展开并动态化，预测于2035年左右我国交通部门碳排放达峰；董健康等[17]通过选取3 个因素构建STIRPAT 模型来预测民航的碳排放量。总体看，传统的预测方法在面对区域交通碳排放复杂的非线性系统且系统中各个因素互不独立的特征时，存在稳定性低、可解释性较弱和关键参数选取困难等不足，导致预测精度不高。 对此，基于统计学习理论的机器学习方法-支持向量回归机（SVR）正广泛应用于碳排放预测。如：陈亮等[18]利用SVR 结合情景分析法预测北京市交通运输业的碳排放；宋杰鲲[19]通过SVR 和情景分析预测未来5年我国的碳排放。

SVR 在实现回归估计时采用ε-SVR 和v-SVR 2 种方法。 其中ε-SVR 法适合有限样本，理论上可获得全局最优点，有良好的推广能力，且计算复杂度与样本维数无关，故选用ε-SVR 法结合情景分析进行预测。

1 材料与方法

1.1 影响因素选取

“十三五”期间，江苏省交通运输业能耗强度明显降低，污染物排放得到了有效控制，但要实现碳达峰，仍存在能源消费结构有待优化和科技创新支撑不足等问题。 结合ZHANG Chuan-guo 等[20]通过STIRPAT 模型对碳排放影响因素的研究成果，并考虑数据的可获得性，选取人均GDP、客运周转量、货运周转量、 能源结构和碳排放强度5 项影响因素作为江苏省交通运输业碳排放预测的自变量。其中，人均GDP 反映了区域经济强度的影响；客、货运周转量反映了交通行业自身的影响； 能源结构和碳排放强度反映了交通运输业科技发展水平的影响。 碳排放强度是指单位GDP 增长带来的碳排放量，计算方式如下：

式中：I 为碳排放强度，t/万元；C 为交通运输业CO2排放量，t；G 为交通运输业经济总值，万元；t 为时间。

能源结构为不同能源消耗转换标准煤用量与交通运输业消耗能源总量的比值，计算公式如下：

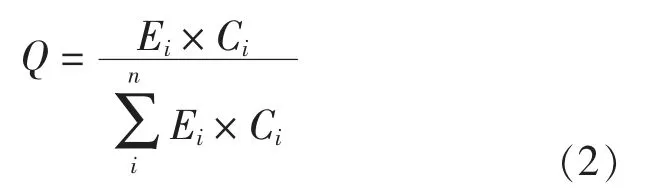
式中：Q 为能源结构，%；E 为能源消耗量，t；C 为能源转换标准煤的转换系数；i 为能源类型，包括原煤、汽油、煤油、柴油、燃料油、电力和天然气。

1.2 建立基于ε-SVR 的碳排放预测模型

线性训练集T=｛ （x1,y1），（x2,y2），…（xi,yi），…（xn,yn） ｝,xi∈Rn,yi∈R,i=1,2,…n。 其中：xi为输入向量；yi为输出值。

设Rn上的一个线性函数表达式为：

式中：ω 为权值向量；b 为偏移常量。

根据数理统计学理论，函数估计可转化成以下公式：

式中：ε 为不敏感损失函数阈值。

为解决个别数据在ε 精度下不能完成估计的问题，引入松弛变量，把优化过程转化为对偶问题求解。 对偶问题和回归函数均只涉及样本输入间的内积运算（xi,yi），因此引入核函数K（xi,yi），将线性回归问题转化成Hilbert 空间中的非线性回归问题，构建模型为:

根据2000年～2019年江苏省交通运输业碳排放及各项影响因素组成的样本集。 构建模型如下：

（1）对自变量和因变量进行归一化处理，保证所有的数据均在[0,1]之间。

（2） 在样本集中随机选取10 个样本组成训练集，剩余样本组成测试集。 选择径向基核函数K（xi,x）=处理训练集并构建模型。 设定较小的ε 初始值，将lbC 和lbγ 的取值范围分成若干网格； 将所有样本均分为v 组即应用v 折交叉验证；固定网格上的一个参数对（C，γ），寻求均方误差（MSE）最小的参数对。如误差较小，则得到最优参数；否则逐步增大ε 值，直至误差值满意为止。

（3）对训练集的数据进行仿真，得到模型最优解和回归函数，将训练集和测试集的全部数据代入函数并输出拟合值，并对拟合结果与真实数据进行线性回归，依据相关系数判断模型的学习推广能力，若模型学习推广能力差，则返回上一步。

（4）将预测年限交通运输业碳排放影响因素值xi0按照式（8）进行归一化处理，代入回归函数后输出结果并对其依照式（9）进行反归一化处理，可求得预测年限的交通运输业碳排放数据。

2 结果与分析

2.1 数据来源

采用“自上而下”的方法计算CO2排放量，即基于交通运输工具燃料消耗的统计数据计算，计算公式如下：

式中：ECO2为CO2排放量，万t；Ej为燃料消耗量，万t；Fj为燃料碳排放因子。

Ej数据来源于 《中国能源统计年鉴》； 人均GDP、客运周转量、货运周转量和碳排放强度数据来源于《江苏统计年鉴》。尽管电力在使用端是清洁的，但我国的发电结构证明电力并不是完全清洁的，故采用生态环境部发布的电网排放因子计算碳排放量。 不同燃料的碳排放因子[21]见表1。 碳排放量及影响因素数据见表2。

表1 不同燃料的碳排放因子 t·t-1

表2 碳排放量及影响因素数据

2.2 结果分析

依照模型构建的步骤，随机选取训练集和测试集。ε 的初始值为0.01，C 和γ 的取值范围为[2-10，210]，网格宽度为0.5，采用10 折交叉验证法，最终得出C*值为1 024.0，ε*值为0.011，MSE 值为0.000 4。 分别对训练和测试的样本进行拟合，得到预测值与原始值的线性回归结果分别见图1 和图2。

图1 训练结果线性回归

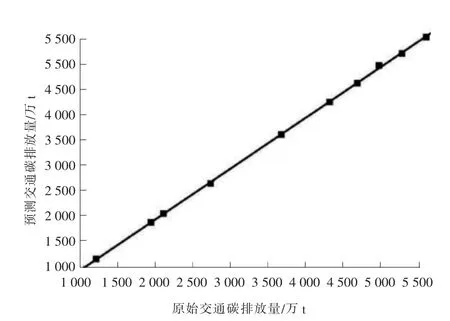
图2 测试结果线性回归

由图1 和图2 可知，训练样本的相关系数为0.991 0，均方误差为0.001 1；测试样本的相关系数为0.999 8，均方误差为0.000 046。 由此说明，模型具有良好的学习和推广能力，可作为碳排放的预测模型。

3 江苏省交通运输业碳达峰预测

3.1 影响因素标定

根据《关于完整准确全面贯彻新发展理念做好碳达峰碳中和工作的意见》（以下简称《意见》）、《江苏省国民经济和社会发展第十四个五年规划和二〇三五年远景目标纲要》（以下简称《纲要》）等相关资料，获取江苏省交通运输业碳排放5 项影响因素数值。

共设置基准、低碳和强化低碳3 个情景。各情景下影响因素的变化率见表3。

表3 不同情景下5 个影响因素的变化率 %

（1）人均GDP

《纲要》提出：“十四五”时期地区生产总值年均增长5.5%左右，到2025年人均地区生产总值超过15 万元” 的目标，《经济蓝皮书：2021年中国经济形势分析与预测》 中 “预计中国2020年GDP 上升2.2%左右，2021年GDP 上升7.8%左右”。 结合国家统计局数据，中国虽已进入老龄化社会，但随着三胎政策施行，人口继续增长，故预测人均GDP 将以较慢速度增长。

（2）客、货运周转量

“十三五”时期江苏省客、货运周转量年均增长率分别为2.6%和11.0%；新冠疫情对交通运输业的影响较大，未来人们更多的是短距离出行，且在新常态的经济发展模式下，由于科技发展进步，货物的运距趋于合理化，重复和迂回运输减少，故在“十四五”后客、货运周转量将出现小幅度下降趋势。

（3）能源结构

2000年～ 2019年能源结构年均增长率为7.6%。 《交通强国建设纲要》中提出“优化交通能源结构，推进新能源、清洁能源应用，推动城市公共和城市物流配送车辆全部实现电动化、 新能源化和清洁化”。 《意见》提出“到2030年，非化石能源消费比重达到25%左右” 。 由此可见，加快能源转型、提高清洁能源使用比例已成为必然趋势。

（4）碳排放强度

《意见》提出“到2030年单位国内生产总值二氧化碳排放比2005年下降65%以上”。 江苏省交通运输“十四五”发展目标提出“到2025年，江苏省实现智慧绿色安全交通走在全国前列” 。 经济增长与碳排放脱钩成为必然趋势，故3 种情景下碳排放强度将以不同速度降低。

3.2 结果与讨论

将3 种情景下的影响因素预测值代入ε-SVR模型，基准和低碳情景下的预测样本相关系数大于0.9，强化低碳情景下相关系数大于0.8。 将碳排放预测数值进行处理后。 所作趋势线见图3。

由图3 可知，从上到下分别是基准、低碳和强化低碳情景的碳排放趋势线，相关系数分别为0.998 2，0.997 5 和0.997 7。其中，基准情景下，江苏省交通运输业碳排放将于2044年达峰，排放峰值为35 989万t；低碳情景下, 碳排放将于2038年达峰，峰值为22 684 万t；强化低碳情景下,碳排放将于2036年达峰，峰值为16 357 万t。

图3 3 种情景下碳排放预测结果变化趋势

上述结论与以下研究基本一致。 ZHU Changzheng 等[22]利用SVR 结合情景分析预测，高碳情景下中国交通运输业碳排放达峰时间为2046年，基准情景下为2040年，低碳情景下为2036年。CHEN Xi等[23]采用库兹涅茨曲线预测，我国交通运输业碳排放将在2043年达峰；可见江苏省距“强富美高”新江苏的总体定位和“两个率先”的目标任重道远。

4 结论

根据2000年～2019年江苏省交通业碳排放数据，选择人均GDP、客、货运周转量、能源结构和碳排放强度5 个影响因素，构建ε-SVR 模型，结合情景分析预测碳达峰，得出以下结论：

（1）模型的训练和测试数据集拟合的相关系数均在0.99 以上，均方误差不超过0.002，表明所选模型具有良好的适用性。

（2）3 种情景下江苏省交通运输业将分别将于2044年、2038年和2036年实现碳达峰。

（3）通过适度降低经济发展速度；提高清洁能源利用率；加快优化运输业结构，降低能源消耗[24]；促进运输工具更新换代等手段均可加速实现碳达峰。此外，国家也可通过降低企业减排的成本和风险，加强对减排技术的保护和支持，将社会路径与科技路径结合起来，控制交通运输业碳排放量，以实现2030年前碳达峰的目标。