例谈IYPT赛题研究中高中生物理建模能力培养

周洋平 陆建隆

（南京师范大学教师教育学院，江苏南京 210097）

本文以国际青年物理学家竞赛（Inter national Young Physicists'Tour nament，简称IYPT）赛题为基，以Hallown提出的科学建模过程模式理论为依据，例示针对IYPT 赛题的研究过程在高中生物理建模能力培养中的作用，与此同时给教师提供了一个在高中依托IYPT 培养学生物理建模能力的设计参考.并以笔者命制的2021 年IYPT赛题为例说明教师如何从资源使用走向主动的资源开发，从而形成“理解—设计—实施—开发—深化”赛题物理建模能力培养功能的良好闭环.

1 理解——赛题物理建模能力培养功能的发掘

1.1 物理建模与物理建模能力

从不同的视角出发对于物理建模活动有不同的理解，更多采用的是从心理学视角出发的将物理建模定义为对研究对象进行表征的过程.此外从科学教育或科学学科视角出发也可将物理建模定义为一种科学实践活动或一种科学思维方法.将多个视角进行整合，即可认为物理建模是一项“个体对研究对象进行表征从而建构物理模型并形成用模型解释、预测现象的科学思维能力的科学实践活动”.物理建模能力定义为：是个体具备一定的物理建模意识，并能够从实际问题中提取出若干核心要素及要素间联系，进而构建物理模型从而解释、预测现象的能力.这也与《中国高考评价体系》中的科学思维相吻合.图1呈现了“物理建模”与“物理建模能力”的关系及内涵.当落实于实际情况下学生物理建模能力的培养，还需进一步理解物理建模能力是认知能力与非认知能力相统一的智能系统，分别对应于个体参与科学实践活动所需要的基础能力与过程中的心理动力，物理建模能力最终体现为个体建构物理模型并应用于实际问题解决的水平.

图1 物理建模与物理建模能力内涵

1.2 IYPT 赛题特点

IYPT赛题的特点促使其成为培养高中生物理建模能力的良好载体.如表1所示第31届IYPT第14题“提灯辐射”，其要求学生探究夜晚从提灯中发射出数条射线这一现象并解释其产生原因.上例体现了IYPT 赛题的开放性、探究性、科学性、趣味性.其开放性使得学生面对实际情境下的问题或原始物理问题，趣味性催生学生进行探究的心理动力，由此物理建模在学生对问题表征的过程中悄然展开.而赛题的探究性与科学性保证了在实践过程中，学生必然需要经历习得基础知识与能力、对问题进行进一步表征、提取核心要素及关系最终构建能够解释或预测现象的模型的科学实践过程，物理建模能力已然贯穿在了这一实践过程中.

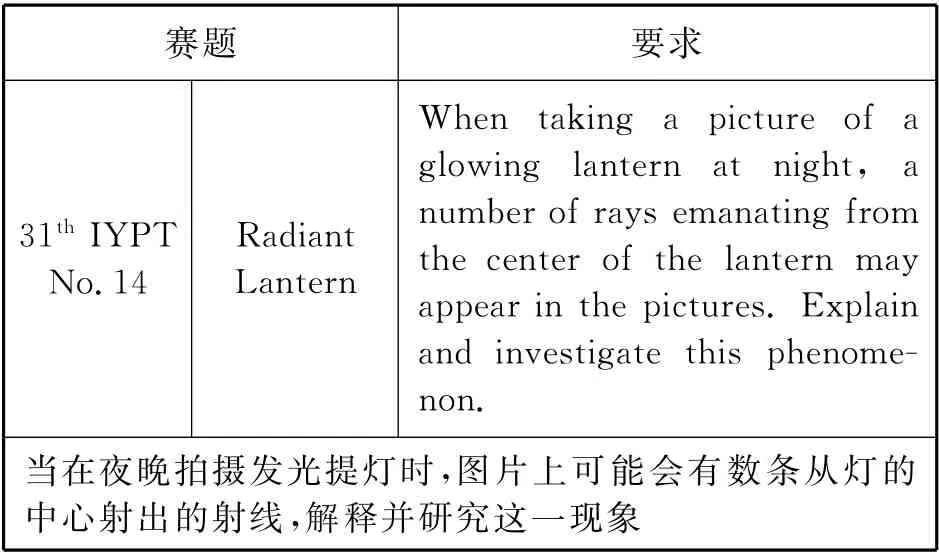
表1

2 设计与实施——基于建模过程模式理论的实践路径

2.1 科学建模过程模式理论

针对物理建模能力培养的教学实践基于Halloun 的科学建模过程模式理论设计.其认为在解决一个问题时，物理建模需要经历5个过程，如图2所示，分别是模型的选择、建构、验证、分析以及部署.

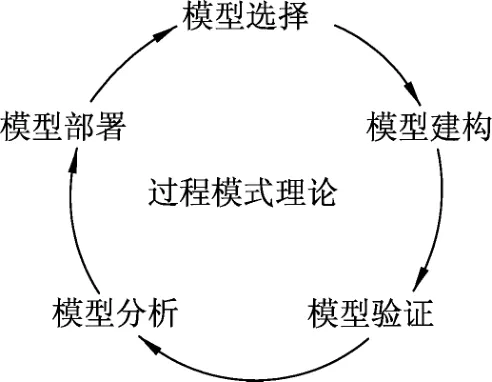
图2 建模过程模式理论

建模总是始于对模型的选择，选择基于对与理论相关的各个熟悉的基础模型，会受到探究目的、模型使用范围以及模型效度等因素影响.这也即此前表示需要学生具备科学实践中基础知识与能力的原因.当然在解决问题的过程中基本能力也能够得到培养.在选择了一个或数个基础模型后，随后需要对模型进行建构与验证，这两步常常同时进行.在这一阶段，需要引导学生基于所选择的基础模型，对问题进行或定量数学表征或定性描述，但并非要求学生穷尽对所有细节的处理.其主要目的在于使学生利用模型把握问题概貌.在此过程中，同步检验基础模型的选择是否合适，修正、提升基础模型的效度及内部一致性.在问题的模型框架已经搭建且具有较好的内部一致性的条件下，便需要引导学生使用定量或定性的方法具体求解模型并解释结果.最终，引导学生基于所使用的模型与模型求解结果对问题进行解释、对现象进行预测等.如果所采用的模型或模型求解方法具有普适性，还可借此促使学生形成可迁移能力.同时，模型的求解、问题的解决在某些情况下还能够被用来修正学生原本认知中的知识等.

2.2 设计示例：“提灯辐射”

教学实践的设计与实施依循建模过程模式理论，在此以第31届IYPT 中第14题“提灯辐射”为例，结合笔者指导高中生进行IYPT 的经验，说明如何基于赛题开展高中生物理建模能力培养的教学实践活动.表2给出了教学实践的设计框架，包括建模活动中各环节对应的主体活动以及完成相应活动所需或所培养能力的表征.

表2 高中生物理建模能力培养教学实践设计框架

2.2.1 模型选择

模型的选择依赖于对实际问题的观察以及对实际问题中核心要素的把握，因而这一阶段教师需要有意识地引导学生主动尝试拍摄如图3所示的问题现象（提灯辐射）并进行观察，同时根据已有知识对现象的产生原因进行猜测.

图3 预实验——拍摄并观察提灯辐射现象

预期达到的目标是在教师的引导下，学生能够结合所学光学知识猜测现象中射线产生的原因是光的衍射.而基于对相机中主要部件原理的理解，可以推测衍射现象最可能出现在相机的光圈处.相机光圈为正多边形结构，根据衍射现象产生的条件，可以进一步推断是从远处射来的光线在光圈的边缘处发生衍射产生射线.因此暂且选择单边衍射模型、正多边形孔衍射模型以及远场衍射模型作为本问题的基础模型，提取出核心要素为光源、小孔、距离、衍射等.

2.2.2 模型建构与模型验证

在选取了模型后，教师需要引导学生使用模型或定量或定性地对问题进行模型化表征，同时验证所选取模型是否合理、有效，模型间是否具有内在一致性.

在针对本例的建模活动中，学生可以采用前述单边或多孔衍射模型对问题进行描述.具体表现为通过对如图4所示单边衍射模型衍射光强的数值仿真，学生可以发现光线在边缘处发生衍射，且衍射出的光线与边缘的垂直平分线重合.单边衍射模型可以理解为相机光圈正多边形结构中的一条边，在此模型中衍射出的光线构成了提灯辐射现象中的一个基本单元.

图4 单边衍射模型及衍射光强分布

在此过程中，还需提醒学生验证模型选取的正确性，例如夫琅禾费衍射这一远场近似衍射模型的选取是否合适？从而确定后续的进一步探究是否使用这一模型，亦或是更换衍射模型.当学生无法独立解决时，教师应当给予学生必要的知识补充，例如针对远场近似使用的判断，告知学生可以采用菲涅尔数Nf进行验证.如果波长为λ的光先通过孔径为a的孔然后传播了L的距离，将本问题中的相关数据带入菲涅尔数计算公式，得到菲涅尔数为为1422.5.而只有当菲涅尔数小于1时，才能采用夫琅禾费衍射，据此修正本问题中的衍射模型为菲涅尔衍射.

随后即可引导学生根据单边衍射及菲涅尔衍射模型构建正多边形孔衍射模型（正多边形孔模型由数个单边模型组合而成）.在模型验证及模型表征的过程中，暗含了处理核心要素间关系的要求，一方面需要学生理清光源与光圈以及光圈与CCD 间距离对衍射模型选取的影响，另一方面也需要学生理清单边衍射与正多边形孔衍射间关系.处理好核心要素间关系后，最终将问题模型化表征为光通过正多边形孔产生菲涅尔衍射，如图5所示.

图5 提灯辐射现象的模型化表征

除定性的描述外，在教师的指导下，学生也可以引入菲涅尔 基尔霍夫公式来定量表征到达CCD 上的光振幅分布（衍射图像），其表达式为

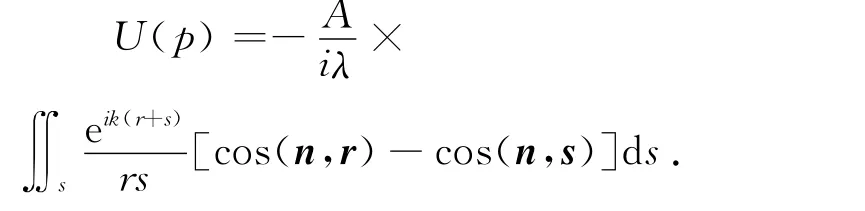
2.2.3 模型分析

在将问题物理模型化后，需要通过对参数进行求解、对模型进行分析，引导学生加深对模型的理解，为在模型部署阶段解释现象产生原因及模型参量对现象的影响作准备.

从定性分析的角度，可以引导学生尝试分析正多边形边数与衍射图样射线条数间关系.正多边形孔模型是由数个单边模型组合而成，在光圈的一条边上可以产生沿中垂线辐射出去的两条射线，且两射线间的夹角为180°.因此当多边形的边数n为偶数时，相互平行的两边的衍射条纹会发生叠加，最终表现出来的条数应当为n条.如果边数n为奇数，也就不存在相互平行的两边，每条边都会发出两条射线，最终表现出来为2n条.

从定量分析的角度，可以引导学生从模型的定量表征——菲涅尔 基尔霍夫公式入手，分析其中变量对模型求解结果的影响.根据公式表达，可以确定出如表3 所列研究参量，随后可以通过实验或数值仿真的方式对参量进行研究.这一过程对学生科学实践活动基础能力提出了较高的要求，教师需要及时、适切地给予学生知识的补充、方法的提点，从而提升学生物理建模能力中所需的科学实践基础能力.

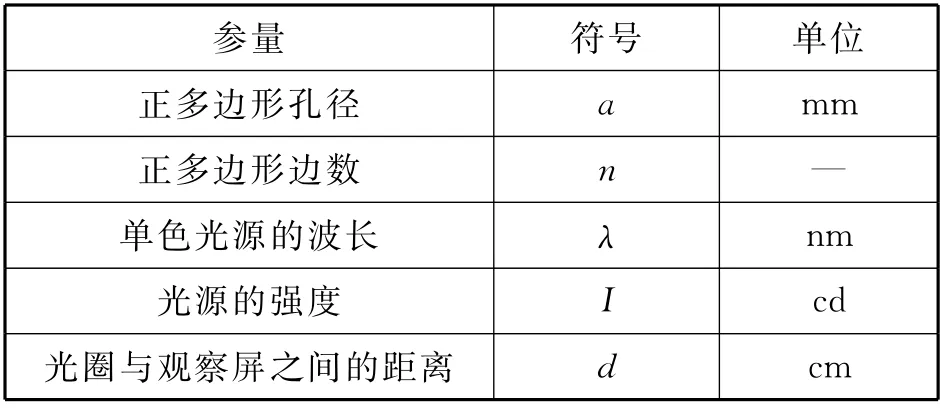
表3 研究参量

2.2.4 模型部署

在经过了模型的选择、建构、验证及分析后，学生已经对问题所属的模型有了较为清晰的认识，也分析了主要参量对模型的影响.此时教师即可鼓励学生使用模型来解释现象或通过解释参量对模型的影响来预测现象，具体的操作形式可以是个人或小组的汇报、研究报告撰写以及学术辩论赛等.其核心在于促使学生以各种方式对建模、解模的过程进行表达，在表达、讨论或者辩论的过程中，加深对模型的理解，强化物理建模的过程，激发可迁移能力.

3 开发——走向物理建模能力培养资源的主动探索

高中阶段学生的科学思维正处于焕发蓬勃生机的时刻，但尚未完全形成，因而在基于IYPT 赛题研究的物理建模能力培养活动中，教师所发挥引导、辅助功能的效度是培养目标能否达成的核心影响因素.教师固然可以在透彻理解建模过程模式理论以及明晰基于IYPT 赛题研究的能力培养实践路径的基础上，使用每年更新的赛题，推进高中生物理建模能力培养的工作.然而就如参与命题工作对于教师的重大意义一样，当教师对于IYPT 赛题能够从主动使用资源更进一步转换为主动开发资源，从正向使用走向逆向设计，对这一培养活动的理解将发生质变.

赛题的开发需要从两方面入手，一方面是IYPT 赛题的特点，另一方面是物理建模能力培养的教育目标.首先从IYPT 赛题所具有的开放性、探究性、科学性、趣味性特点入手，赛题需要选取开放性的原始物理问题，其现象应是有趣的，其蕴含的物理模型与模型所对应的物理原理应是高中学生可探究的，由此可粗筛数个满足特点的赛题并勾勒赛题的框架.随后从物理建模能力培养的教育目标着手，考虑目标所期望得以体现的模型、能力要求等，从圈定的数个赛题中精筛出契合的赛题，并进一步通过设计针对性的要求使得赛题最终精准地指向某一目标的培养.经历这样的设计过程，教师将真正融入到基于IYPT 的科学实践中去，更为深入地理解IYPT 赛题在建模能力培养中的作用.自行设计的赛题在教学实践中使用起来也更为得心应手，对关键环节或问题的处理也更细致入微.据此开发思路，笔者命制了2021年第34届IYPT 第10题“旋转漂移”（Spin Drift：When a ring is set to r oll in a parabolic bo wl，interesting motion patter ns may arise.Investigate this phenomenon）.

4 深化——从科学探究走向科学实践的培养优化

21世纪初所掀起的科学探究的教育浪潮在物理教育的发展过程中却逐渐演化为对科学探究模式化、固定化、庸俗化的推进和实施.当科学探究变成了要求学生记忆固定的、一成不变的研究步骤，并照葫芦画瓢地认识和感悟科学时，探究便失去了其应有之意.因此对于教师而言，局限于能够理解IYPT 赛题在物理建模能力培养中的意义、能够采用建模过程模式理论进行实践设计、能够主动开发赛题来加深对物理建模能力的理解在长远角度看来是不够的，也是容易陷入模式化、固定化的.

避免科学探究陷入僵局的突破点在于教师走下科学探究或科学实践活动旁观者或纯粹引导者的位置，和学生一起变成科学实践的参与者、行动者.这就要求物理教师首先要能够像科学家一样思考问题，从而能够把握住探究活动的灵魂而非模式化的皮毛，其次才能促使学生在课堂学习共同体的互动中“动脑”、“动手”、“动嘴”、“动笔”，与学生一同经历科学实践，让学生学习真正的科学，充分发挥科学实践对学生能力培养的积极作用.