考虑浸润线不确定性的边坡可靠度分析方法
陈 富,王上上,刘 旭,李 亮,*,彭剑平,高 原,翟 明
(1.青岛理工大学 土木工程学院,青岛 266525;2.招金矿业股份有限公司,招远 265400;3.青岛新华友建工集团股份有限公司,青岛266101)
在水库边坡、尾矿坝坝坡、堤岸边坡中,除了边坡土质、几何参数的影响外,水对边坡稳定性有着重要影响[1],国内外学者对此开展了大量工作。例如孙超等[2]研究了地下水渗流作用对边坡稳定性的影响;还有学者基于ABAQUS,FLAC等数值分析软件研究了降雨以及由此导致的边坡渗流场变化及其对边坡稳定程度的影响规律,研究成果对实际工程具有一定的指导意义[3-6]。由前人研究可知,水对边坡稳定性的影响,一般可由浸润线位置的高低来反映,很多研究都是假设浸润线位置是确定的,然而在实际工程中浸润线的具体位置难以确定,加之气候变化[7-8],降水对浸润线的升降[9-10]也有着影响,给边坡稳定性分析带来困难[11-12]。
本文在考虑土体参数(内摩擦角和黏聚力)不确定性的基础上,利用一正态分布变量模拟了浸润线的随机变化以便研究浸润线不确定性对边坡稳定程度的影响规律。
1 考虑浸润线不确定性的边坡可靠度分析方法
1.1 极限平衡法
极限平衡法是边坡稳定分析最常用的方法之一,这种方法是通过分析边坡失稳时刻滑动土体的静力平衡关系来确定边坡的稳定性,通常用安全系数Fs来评估边坡的稳定程度,Fs越大,边坡稳定性越好,反之亦然。鉴于极限平衡方法发展较成熟,已经发展出许多较完善的商业软件,本文采用商业软件Geo-Studio中的Slope/w模块来求解滑动面的安全系数Fs,在求解安全系数时选用极限平衡法中的M-P法,设置条间力函数f(x)为半正弦函数。
在计算涉水边坡时,水对边坡稳定性有较大影响。根据太沙基有效应力原理,边坡内水的存在势必产生孔隙水压力,由此导致土体的有效应力降低,从而减小土体材料的抗剪强度,最终影响边坡稳定性。在Slope/w模块里通过设置一系列的控制点来确定浸润线位置,这些控制点的坐标信息包括在模型文件里,在批处理计算时,可以通过修改模型文件里的坐标信息来改变浸润线的位置。
1.2 蒙特卡罗方法
蒙特卡罗方法是一种以概率统计理论为基础的数值计算方法。它已经在多个领域得到了广泛应用。现以正方形内切圆面积计算为例,简要介绍蒙特卡罗法的思想。边长为单位1的正方形内有一内切圆,利用蒙特卡罗法计算内切圆面积时,首先在1×1正方形内随机产生N个互不相同的样本点(x1,y1), (x2,y2),…, (xN,yN),其过程如图1所示,其次建立如式(1)所示的极限状态函数,接着由样本点坐标(xi,yi)可以计算出第i个样本点到圆心(0,0)的距离,如此得到N个极限状态函数值G1,G2, …,GN,根据这些样本值可以判断有多少个样本点在圆里,落在圆里点的数量与N的比值就近似为内切圆的面积。
(1)
当G(x,y)≤1时就代表样本点在圆上或圆心里。
本文应用蒙特卡罗方法来计算边坡的失效概率。首先建立关于安全系数的边坡极限状态函数:
G(x,y)=Fs(X)-1
(2)
Fs为安全系数,X=x1,x2,…,xm,m为变量个数,xi为安全系数计算所需要的第i个变量,本文选取土的黏聚力、内摩擦角、浸润线位置作为变量。根据随机变量的分布类型,随机生成N个样本X1,X2,…,XN,代入式(2)中,可计算出N个状态函数值G1,G2,…,GN。若Gi<0,则称Xi为失效样本。统计失效样本个数为M,则边坡的失效概率可近似为Pf:
(3)
其中,Pf的计算精度与抽样次数N有密切关系,所得Pf的变异系数可通过式(4)确定:
(4)
式中:CPf为蒙特卡罗法计算所得Pf的变异系数;Pf为蒙特卡罗方法计算所得失效概率;N为蒙特卡罗方法的抽样次数,欲保证其变异系数为10%时,则N≈100/Pf。
在应用蒙特卡罗法进行计算时,需要进行抽样次数敏感性分析,以保证所得结果具有较高的精度。
1.3 浸润线不确定性模拟
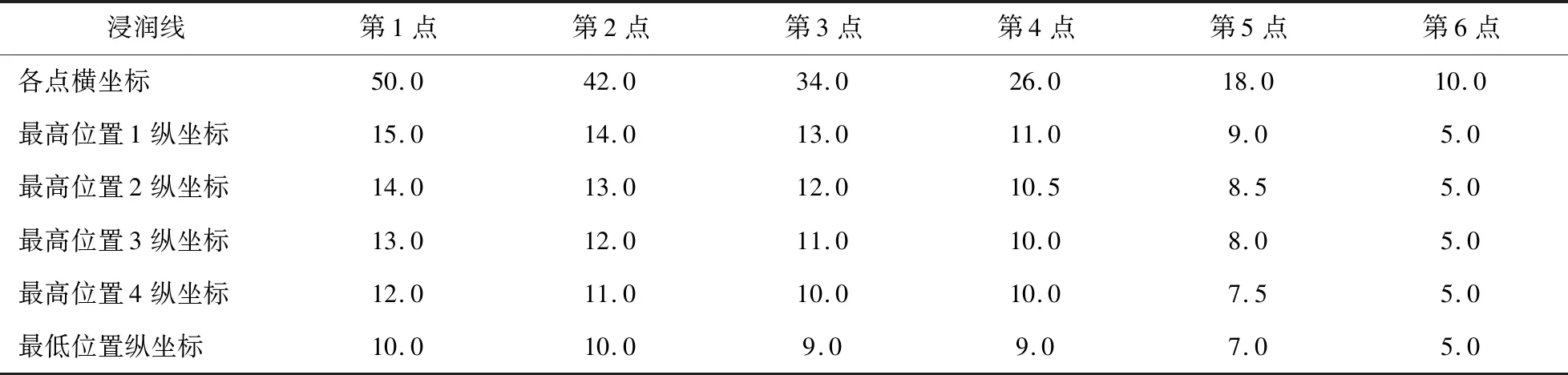
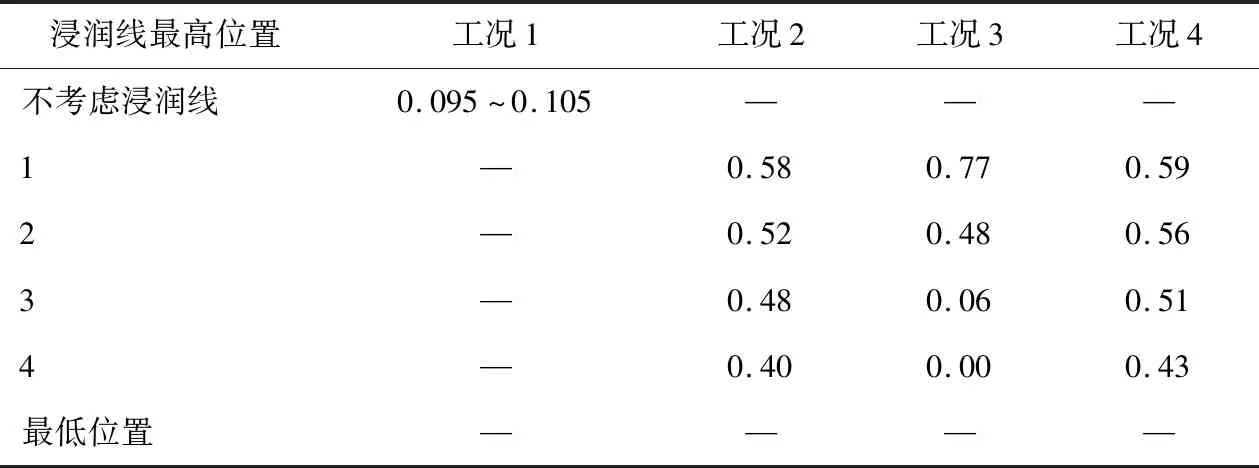
首先确定两条浸润线,分别称之为最高和最低浸润线,这两条浸润线由一系列横坐标固定、纵坐标变化的点确定。如图2所示,设最低和最高两条浸润线上横坐标一致的任意两点为(x,y1),(x,y2),此时两点之间的距离为ymax=y2-y1,介于两点间任意点坐标(x,y3),这点到两点中较低点的距离yw=y3-y1。令k=yw/ymax(0 为研究简单起见,设k值为一符合正态分布的变量,则由k值确定的浸润线亦可视为服从正态分布变化。利用正态分布的3σ法则,可将随机浸润线尽量控制在最低和最高浸润线之间,对于少量越界的浸润线,需要重新生成。如此生成N条服从正态分布的浸润线。根据某k值生成的某浸润线位置如图3所示。 根据式(4)可知,结合浸润线不确定性和土参数不确定性进行蒙特卡罗模拟时,理论上要经过大量的抽样(生成大量的边坡模型),因此采用python程序替代人力来处理大量重复性的工作,此外python程序也可以高效、稳定、准确地生成和计算模型并提取出安全系数进行分析,有利于批处理。 1) 首先在Geo-Studio中利用原始数据(如边坡的几何参数、土体参数、黏聚力c、内摩擦角φ)建立原始边坡的模型,紧接着将模型导出为后缀xml格式的文件。 2) 根据土体基本变量的均值和标准差在python程序中生成该土体基本变量的N个随机变量,此外为生成随机分布的浸润线,先生成N个0~1之间的正态分布随机数k,建立excel格式文件并将这些数据依次输出保存。 3) 接着在python程序中读取excel表格中先前随机生成的土体参数以及随机数k,选取土体参数中的替换原始边坡的土体参数并利用前文所述的方法选取k值确定一条浸润线,依此方法利用python程序重复N次并生成N个新模型放入N个不同的文件夹下。 4) 利用python程序对已生成的N个模型进行批量计算处理。 5) 利用python程序提取已算好模型的安全系数并保存到之前生成的excel格式文档中。 6) 在office程序中统计失效样本的个数M,若N足够大,则M与N之比即为边坡系统的失效概率。 计算流程如图4所示。 考虑如图5所示的均质边坡,坡高10 m,坡角26.6°。该边坡的内摩擦角φ和黏聚力c均为随机变量,根据陈立宏等[13]的研究结论,假定φ和c均服从对数正态分布。c和φ的均值分别为3 kPa和19.6°,变异系数均为0.2,土的单位重度为常量,其值为γ=20 kN/m3。 本文设置如下四种工况来研究土体参数和浸润线随机变化对边坡稳定性的影响:1)仅考虑土体参数不确定性(无浸润线);2)仅考虑土体参数不确定性(浸润线确定);3)仅考虑浸润线不确定性(土体参数确定);4)同时考虑土体参数不确定性和浸润线不确定性。在这些工况中土体参数包括土的黏聚力和内摩擦角,二者均呈对数正态分布;浸润线呈正态分布,设置四种不同的最高浸润线位置(最高位置浸润线坐标变化如表1和图6所示),最低浸润线位置保持不变,呈正态分布的浸润线在最高位置浸润线和最低位置浸润线之间变化。通过python程序给此边坡添加正态分布的浸润线。 表1 最低位置和各最高位置浸润线横纵坐标 m 针对四种工况,各生成1000个边坡模型,共计4000个边坡模型,利用图4所示的计算流程获取边坡失效概率,为保证计算精度,首先进行抽样次数敏感性分析。 以工况1为例,图7给出了不同蒙特卡罗样本下,边坡失效概率的结果变化散点图。由图可知,在样本较少时,边坡失效概率较大,随着样本数的逐渐增多,所得失效概率逐渐降低,最终在0.1上下微小变动,趋于稳定。将pf=0.1代入式(4),计算得到N≈100/pf≈1000时,蒙特卡罗计算结果的变异系数可控制在10%左右。在下文的数值模拟中,蒙特卡罗抽样次数取N=1000。 对设置的四种工况进行数值模拟,计算结果如表2所示。工况1不考虑水的作用,仅仅考虑土体参数的不确定性,由表2可知,在工况1下,边坡的失效概率趋于一致,在0.1上下微小波动;在工况2下,考虑水对边坡的影响,浸润线作为定值来考虑,在浸润线最高位置1时,确定的浸润线取最低位置和最高位置1的平均值,以此类推。在工况2下,在浸润线最高位置1,2,3,4时,边坡失效概率分别为0.58, 0.52,0.48及0.40,边坡失效概率随着浸润线位置的抬升直线增加,浸润线最高位置每抬升1 m,失效概率大约增加0.05;在工况3下,仅考虑浸润线的不确定性,土体参数取其平均值,在浸润线最高位置1,2,3,4时,边坡失效概率分别为0.77,0.48,0.06及0.00,边坡失效概率随着浸润线最高位置的抬升(浸润线变化范围增大)迅速增加,呈非线性增长趋势。 表2 4种工况失效概率的计算结果 在工况4下,在浸润线最高位置1,2,3,4时,边坡失效概率分别为0.59,0.56,0.51及0.43,对比发现:在浸润线位置较高(浸润线最高位置1)时,工况4所得边坡失效概率介于工况2和工况3之间;在浸润线位置较低(浸润线最高位置2,3,4)时,工况3得出的失效概率低于工况2与工况4,工况4略高于工况2。说明在浸润线位置较高时,工况3得出的失效概率偏大,而工况2得出的失效概率偏小,在浸润线位置较低时,工况3与工况2得出的失效概率均偏小。 1) 仅考虑土体参数不确定性时,边坡失效概率随着浸润线最高位置的抬升直线增加,浸润线最高位置每抬升1 m,失效概率增加0.05; 2) 仅考虑浸润线不确定性时,边坡失效概率随着浸润线位置的抬升迅速增大,呈非线性增长趋势; 3) 在同时考虑土体参数不确定性和浸润线不确定性的工况下,边坡失效概率介于仅考虑土体参数不确定性和仅考虑浸润线不确定性之间;在浸润线位置较低时,仅考虑浸润线不确定性时得出的失效概率明显低于仅考虑土体参数不确定性与同时考虑两者的不确定性,并且同时考虑两者不确定性时的失效概率略高于仅考虑土体参数不确定性。说明在浸润线位置较高时,仅考虑浸润线不确定性得出的失效概率偏大,而仅考虑土体参数不确定性得出的失效概率偏小,而在浸润线位置较低时,仅考虑浸润线不确定性与仅考虑土体参数不确定性得出的失效概率均偏小。 4) 在涉水边坡进行可靠度分析时,建议综合考虑土体参数与浸润线位置的不确定性。 需要指出的是,以上结论均是通过理论推演所得,考虑涉水边坡影响因素的复杂性,未考虑非饱和土中的基质吸力对计算结果的影响,对此还需今后进一步研究。1.4 基于python程序的失效概率计算
2 算例
2.1 边坡模型与工况设置
2.2 蒙特卡罗抽样次数敏感性分析
2.3 不同工况下边坡失效概率对比分析
3 结论

