剪裁CAD冲压件的一步逆等几何分析方法
张志功, 刘依娜, 张向奎, 王长生
(大连理工大学 汽车工程学院, 辽宁 大连 116024)
0 引 言
汽车制造过程需要将大量的金属冲压成形。为节省成本,冲压成形数值模拟被广泛应用于汽车设计中。板料冲压成形数值模拟最常用的方法是基于流动理论的增量法和基于塑性变形理论的全量法。
增量法对板料进行冲压成形仿真预测时,需要在每一增量步开始时输入所有参数,虽然结果相对准确,但是计算相当耗时。因为增量法的缺点较多,GUO等首先提出Inverse Approach,该方法可以根据最终构型计算得到初始构型,LEE等提出单步逆和多步逆分析方法。逆成形法是从冲压件的最终构型出发的,所以只需要输入冲压件的最终几何形状CAD模型即可,计算精度低于增量法,但是计算耗时大大减少。
可采用的数值计算方法有很多,例如有限差分法、有限元法和边界元法等。增量法和逆成形方法一般都采用有限元法。先使用伽辽金等弱形式构建数学模型,再对CAD模型进行离散,即可求解所需要的未知量。然而,有限元法一般使用拉格朗日等基函数,由于拉格朗日基函数的插值性质,模型离散过程会改变模型的CAD数据,拉格朗日单元的前处理过程也相当耗时耗力。针对以上缺点,HUGHES等提出等几何分析法,以解决有限元方法无法精确表达CAD模型的缺陷。一步逆成形法分可为初始解算法和塑性迭代算法。ZHANG等将IGA应用于一步逆成形方法中,开发板材冲压一步逆成形等几何分析初始解快速预示算法,其分析结果表明该方法在计算效率、求解精度和鲁棒性等方面具有很好的效果。WANG等利用可塑性全变形理论,将一步逆成形算法与等几何分析方法相结合,提出一步逆等几何分析方法,该方法在不损失CAD数据的情况下具有很高的精度和准确性。WANG等借用TSA方法与Nitsche方法解决等几何一步逆初始解算法无法计算复杂剪裁多片模型的限制,为进一步采用等几何一步逆塑性迭代算法计算复杂多片剪裁模型奠定基础。
根据张量积型NURBS曲面的特性,NURBS曲面表示复杂模型时需要进行裁剪。BEER等使用规则张量积曲面重构被剪裁曲面有效区域,此方法计算程序非常简单,但是不能重构复杂的模型。XIA等使用三角形Bézier曲面转换剪裁模型,将剪裁模型转换成C0连续的小平面模型。WANG等使用准一致方法处理剪裁曲面,该方法的主要优点是可以直接采用单元的边界曲线进行数值积分。KIM等提出TSA方法,其核心在于计算积分点,主要通过曲线插值和多次坐标变换完成。SCHMIDT等使用独立曲面对剪裁区域进行局部重构,其核心在于曲面逼近,一般使用最小二乘法。
本文利用Bézier曲面重构剪裁单元并计算剪裁单元的刚度矩阵,然后通过转换矩阵将其转换到NURBS曲面上,以实现剪裁单元的处理,进而将此方法应用到等几何一步逆法中。
1 NURBS曲面的剪裁算法
1.1 剪裁交点的搜索算法
一般使用B样条对NURBS曲面进行剪裁。与计算机图形学不同的是,等几何分析需要求出B样条和NURBS曲面在NURBS曲面参数空间中的交点,方便后续进行数值积分等工作。对于样条曲线或者曲面来说,其拥有2个空间,一个是参数空间,一个是物理空间。B样条曲线的空间为一维向量,参数为,而NURBS曲面的空间为二维平面,参数为(,),与(,)相互独立,不存在任何联系。为使剪裁曲线B样条与NURBS曲面处在同一个物理空间中,必须建立与(,)之间的联系,即得到参数在物理空间的坐标(,,),同时找到该坐标在NURBS曲面空间的(,)值,需要推导将曲线参数对应到物理空间坐标(,,)、再反演到NURBS曲面参数空间的标(,)的联系。
求取剪裁交点的程序实现流程如下:
(1)对剪裁曲线进行节点插入细化,在参数空间中得到大量采样点的值,将其命名为Line-t。
(2)采用NURBS曲面公式计算Line-t对应的物理空间的坐标(见图1),将其命名为Line-xyz。

图1 细化后剪裁曲线节点向量映射到被裁剪曲面的参数点
(3)Line-xyz同在NURBS曲面上,利用NURBS曲面公式和Newton迭代法,将Line-反演到NURBS曲面上,得到相对应的NURBS参数空间的Line-和Line-。
(4)剪裁曲线节点向量在NURBS曲面的参数空间见图2。绿色的方点为交点,红色的圆点为采样点,每一交点都被包含在(,)~(+1,+1)区间中,并且任意一个区间仅包含一个交点或者不包含交点,以保证正确求解所有交点。

图2 剪裁曲线节点向量在NURBS曲面的参数空间示意
(5)根据(,)和(+1,+1)点,令
=|-+1||-+1|
(1)
=+|+1-|
(2)
即可以得到NURBS曲面参数+1对应的B样条参数。
(6)利用NURBS反演函数计算相对应的(,)。
(7)比较与+1的差值是否在误差范围内:若差值在误差范围内,即认为求得交点;若与+1的差值不在在误差范围内,则继续计算(8)。
(8)判断(,)所在的网格区间,即是在+1左侧还是右侧:若是在左侧,则将(,)赋值给(,);若是在右侧,则将(,)赋值给(+1,+1)。
(9)继续循环(5)~(8),得到误差范围内的所有交点,即认为交点求出。将得到的交点按照曲线节点向量大小排序,以便后续单元分类。
(10)若后续计算中发现得到的交点不全,则需要回到第一步,继续加密剪裁曲线,直到正确求解所有交点且没有遗漏。
1.2 剪裁单元分类
为方便剪裁单元的重构,需要人为地对剪裁单元进行分类,某剪裁后的单元分类示意见图3。剪裁单元可按照形状进行分类:红色的三角形单元设定为类型A,绿色的四边形单元设定为类型B,深蓝色的五边形单元为类型C,左侧浅蓝色网格为需要保留的单元,设定为类型S,右侧没有颜色的单元为丢弃的单元,设为类型D。
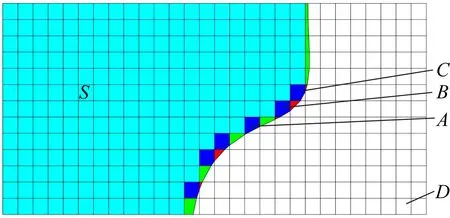
图3 剪裁后的单元分类示意
由于Bézier曲线参数空间的节点向量是按照从小到大排列的,故最小节点位置通常被认为是曲线的起点,可以利用这个特点判断要保留的单元。例如,可以人为设定剪裁曲线的左侧为保留单元,右侧单元不保留。常见的剪裁单元示意见图4(单元的分类与前文一样)。
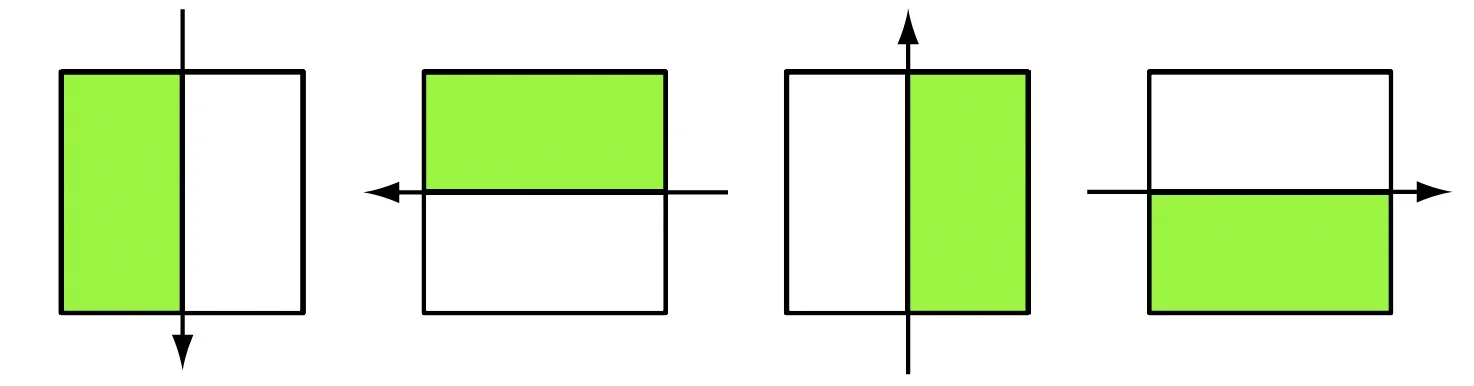

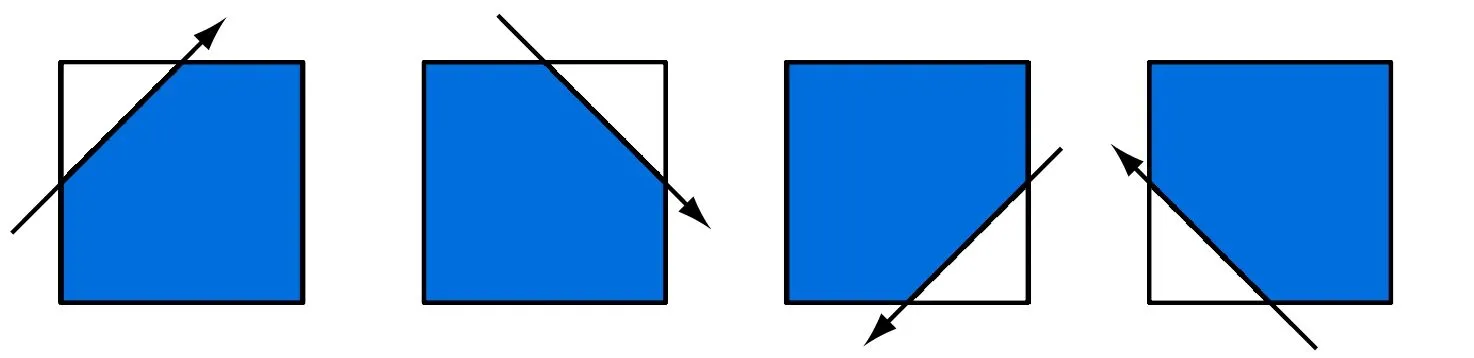
图4 常见的剪裁单元示意
此外,还有可能出现剪裁线穿过单元角点的情况,虽然在实际计算中这种情况非常罕见,但是编写程序时要注意这种情况,以增强程序的鲁棒性。
1.3 剪裁单元重构
为方便计算,使用Bézier曲面对剪裁单元进行重构,使用最小二乘法逼近重构曲面与被重构曲面。为使重构曲面的精度足够高,重构曲面的阶数应不低于剪裁曲面。
使用最小二乘法重构剪裁曲面,需要分别在2个曲面的参数空间内选取配点,配点要尽量均匀,同时因为Bernstein基函数与NURBS基函数具有边界插值性质,所以配点必须在曲面边界上选取。Bézier基函数描述的曲面与NURBS基函数描述的曲面是等价的,即
∑(,t,,t)=∑(,)
(3)
则个配点的等价公式为
·==·
(4)
其中,

(5)

(6)

(7)
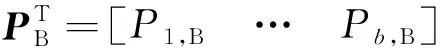
(8)
式中:为剪裁NURBS单元的基函数矩阵;(,)为之前选取的配点所在参数点的基函数值;为剪裁NURBS单元的控制顶点;为重构曲面的Bernstein基函数矩阵;为Bézier曲面的控制顶点,是整个方程中的未知量。
利用最小二乘法计算,
=(·)··()·
(9)
由此可知,用于重构的Bézier曲面的控制点可以通过原始NURBS曲面的控制点转换而来,即
=·
(10)
式中:为转换矩阵,
=(·)··()
(11)
2 剪裁NURBS曲面与一步逆成形法的耦合
2.1 剪裁一步逆等几何分析法初始解预示
剪裁单元重构后,初始解部分的求解与未重构部分相同,都有完整的基函数支撑,区别在于有一部分单元不再是部件的一部分,所以不再对其进行求解。
根据一步逆初始解算法,重构后的单元在局部坐标系下初始单元节点的位移可以表示为

(12)
单元的应力可以表示为
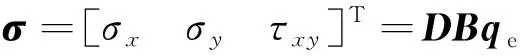
(13)
最后,得到整体坐标系下的节点内力为
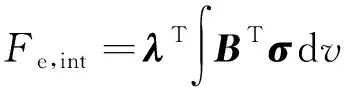
(14)
迭代公式为
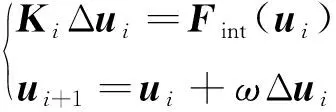
(15)
式中:Δ为节点位移增量;为松弛因子。是根据能量因子决定的,0<<1。残余力矢量与Δ相乘即可求得能量因子。一般来说,能量因子越大,越小。
迭代上述公式,直到内力达到平衡状态,使用位移节点向量的范数判断计算收敛,
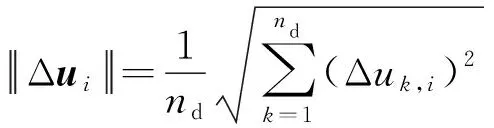
(16)
式中:为板料的总节点数。

2.2 剪裁一步逆等几何分析塑性迭代求解
塑性迭代可计算材料冲压时的应力、应变和厚度的变化,刚度矩阵计算参照文献[19],根据Newton-Raphson迭代法求解非线性方程,即

(17)
式中:为迭代步时的残余力;()为节点外力;()为节点内力。
位移场更新公式为
+1=+Δ
(18)
因为一步逆成形算法中没有施加边界条件,所以添加刚度阻尼(>0)使刚度矩阵非奇异,即
,+Δ=
(19)
为加快迭代收敛速度,可使刚度阻尼系数取值较小。
3 数值算例
3.1 剪裁S梁算例
计算一个剪裁的S梁模型(见图5),此模型是NUMISHEET96的标准考题。原始S梁模型为双二次张量积型NURBS曲面,共有控制点784个、单元676个。为验证算法的准确性,只裁掉S梁的一小部分,非剪裁单元保留624个,剪裁单元个数为26个。用2种不同方法计算出S梁的厚度云图和等效应力云图,结果分别见图6和7。2种方法求出的厚度与等效应力分布几乎相同,等几何方法求出的结果云图更平滑一些。2种方法得到的厚度与等效应力的最大值、最小值以及二者的相对误差见表1,厚度与等效应力结果相对误差都在可接受的范围内。
图5 剪裁S梁示意
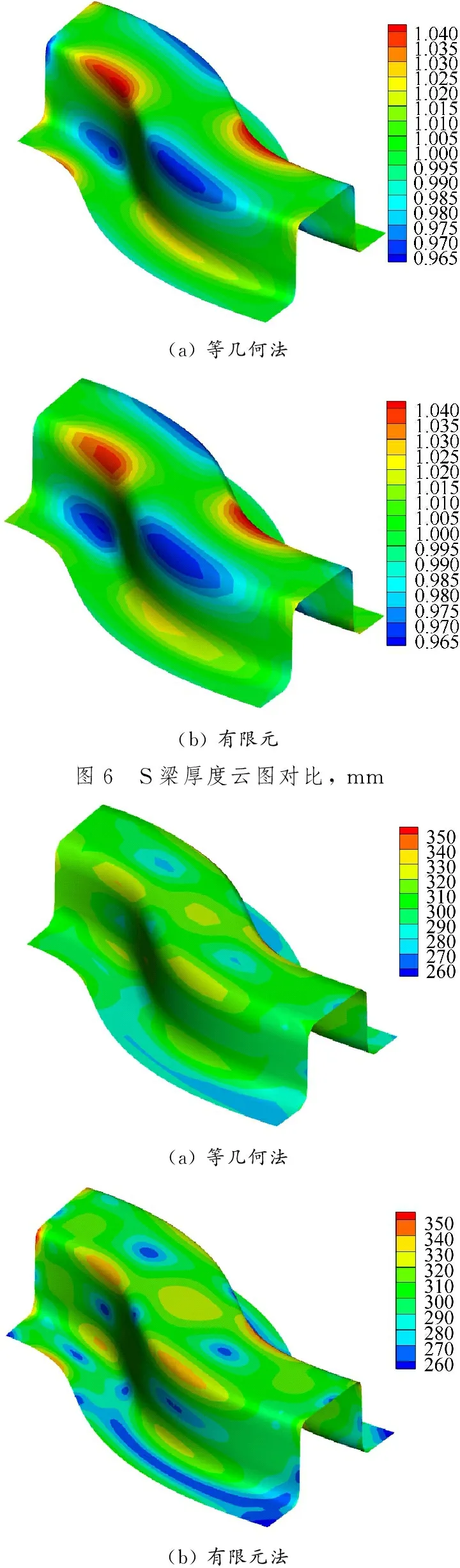
图7 S梁等效应力云图对比, MPa

表 1 S梁算例有限元法与等几何法结果对比
4.2 引擎盖算例
汽车引擎盖是汽车最具有代表性的冲压件之一。同时使用剪裁一步逆等几何方法和有限元法计算一个引擎盖算例,见图8。该引擎盖未剪裁的双CAD数据为二次NURBS曲面,共有450个控制顶点、364个单元,剪裁后共有保留的剪裁单元为298个,删除剪裁单元30个。2种方法计算得到的引擎盖的厚度云图和应力云图分别见图9和10,可见2种方法计算结果的一致性较高。

图8 剪裁引擎盖NURBS曲面和控制网格
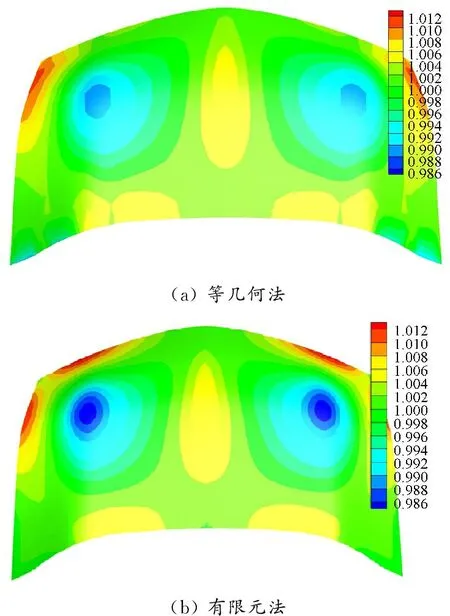
图9 引擎盖厚度云图对比, mm
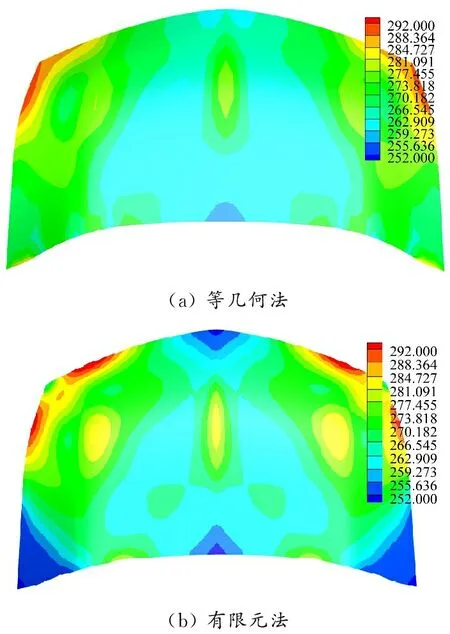
图10 引擎盖等效应力云图对比, MPa
2种方法计算得到的厚度和等效应力的最大值、最小值以及二者的相对误差见表2。对于此算例,厚度和等效应力的相对误差极小。
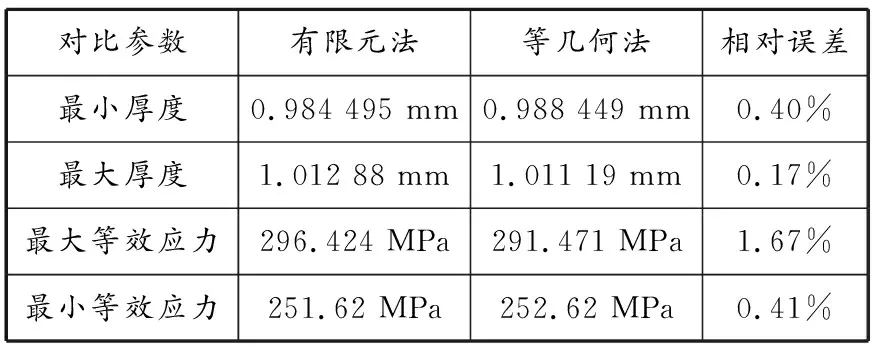
表 2 汽车引擎盖算例有限元法与等几何法计算结果对比
4 结束语
将剪裁算法和等几何分析方法应用于基于一步逆方法的板材冲压成形分析中,构建基于塑性形变理论的剪裁一步逆成形等几何法。首先,预处理被剪裁曲面,包括求取剪裁交点、寻找剪裁单元、剪裁单元分类、剪裁单元重构、剪裁单元组装单元刚度矩阵等;然后,利用初始解算法,展开NURBS模型的控制点网格;最后,利用Newton-Raphson迭代算法处理最终构建的非线性平衡方程,得到最终构型的厚度、等效应力和应变等物理量的分布。
选择不同的模型算例,分别在基于剪裁NURBS曲面的一步逆等几何方法程序和一步逆有限元法程序中进行计算,对厚度和等效应力计算结果及二者的相对误差,验证基于剪裁NURBS曲面的一步逆等几何分析法的正确性和准确性。

