等几何分析与近场动力学耦合的壳结构裂纹扩展仿真算法
夏阳, 王洪帅, 郑国君, 申国哲
(大连理工大学 工业装备结构分析国家重点实验室 汽车工程学院,辽宁 大连 116024)
0 引 言
断裂仿真对壳结构的安全评估具有重要意义。近年来,断裂力学的数值仿真取得快速发展,为业界提供多种可行的解决方案,如内聚力单元法、扩展有限元方法、扩展等几何方法、无网格法、相场方法、分子动力学方法和近场动力学方法等。目前,断裂仿真存在的问题是如何对结构中连续场和非连续场进行统一描述,并且在计算中保证计算效率。为解决这一问题,断裂力学非连续模型与连续模型相结合是一个值得研究的方向。
等几何分析(isogeometric analysis, IGA)直接将精确几何用于数值分析,连通几何设计与数值分析之间的鸿沟,适用于壳结构分析的等几何列式不断被提出,包括无转动的Kirchhoff-Love(K-L)壳模型、带转动自由度的Reissner-Mindlin(R-M)壳模型、实体壳等。基于裂纹扩展问题,将扩展有限元中用到的单位分解法引入IGA中,得到基于K-L理论和R-M理论的扩展IGA(extended IGA, XIGA)方法。XIGA能够模拟裂纹附近的应力场,但是需要额外的准则处理裂纹成核和扩展,在处理裂纹分叉和合并方面存在一定困难。另外一种处理断裂问题的耦合方法是IGA与相场方法耦合。相场方法是建立在Griffith能量断裂准则之上的,该准则是定量描述断裂扩展的经典准则,其核心是假设裂纹扩展过程中的总能量(表面能和体积能)保持最小。AMBATI等采用等几何实体壳单元与相场方法耦合的方式处理壳结构的脆性和韧性断裂。KIKIS等将考虑剪切变形的等几何R-M壳与相场方法相结合,避免体积离散化。为能够得到合适的结果,相场方法必须在裂纹扩展处进行网格细化以满足收敛的要求,导致其需要消耗大量的计算时间。
近场动力学(peridynamics, PD)理论由SILLING提出,用于处理非连续场问题。学者们提出很多用于板壳结构问题的PD模型。TAYLOR等通过将3D模型降为2D,提出PD薄板模型,该模型能够捕获面外弯曲变形,但是只能处理具有特定泊松比的材料。DIYAROGLU等提出考虑剪切变形的薄/厚梁和板的PD列式,其运动方程可以简化为经典Timoshenko梁和Mindlin板方程。SHEN等基于微梁键提出6自由度Euler梁和K-L壳模型,通过插值方法获得键的变形、建立键的微势能,从而得到键的微模量,该模型不限制泊松比。以此为基础,考虑剪切变形,进一步发展出PD R-M壳模型。
由于PD是一种非局部理论,每一个点与其近场域内的一群点相互作用,计算效率比经典的有限元或IGA更低。采用非局部理论和经典连续介质力学理论耦合的方式,其计算效率有望得到提高。将IGA与PD耦合是进行裂纹扩展仿真的一种新的重要方法。MADENCI等提出IGA与PD耦合处理平面问题的方法,将PD点加入到等几何模型中,PD点的自由度与等几何节点相关联,但是PD点不出现在最终的方程中。XIA等提出用于平面弹性问题的IGA-PD耦合模型,使用等几何控制点作为PD点,根据力平衡方法将IGA方程与PD方程相叠加得到待求解线性方程,是一种简单且高效的求解方法。此外,郑国君等使用神经网络预测裂纹扩展路径,快速且准确。
壳的光滑曲面特征使其适于采用IGA方法进行模拟。为对壳结构进行裂纹扩展分析,本文提出一种用于板壳结构断裂分析的耦合模型IGA-PD。采用IGA模型保证几何精确性,将PD模型用于裂纹扩展区域。为直观显示裂纹扩展过程,采用非连续伽辽金(discontinuous Galerkin, DG)方程,提出DG有限元PD板壳单元列式。与粒子点法PD列式相比,采用DG有限元PD板壳单元可以使用高斯点积分,提高计算精度。在耦合过程中,采用力/力矩平衡原理得到耦合模型。将IGA作为边界可以消除PD的表面效应问题,提高PD模型性能。
1 R-M壳的IGA和微梁键模型
1.1 R-M壳IGA模型
采用由三维弹性模型退化得到的R-M壳模型,其几何模型示意见图1。壳变形前采用直法线假设,其物理场采用非均匀有理B样条(non-uniform rational B-spline, NURBS)插值,表达式为

图 1 R-M壳模型示意
(,,)=(,)+·(,)=

(1)
式中:和为节点参数,可分别为由节点向量=[…++1]和=[…++1]定义;∈[-1,1]为壳的厚度;=[],即壳上控制点的位置矢量;(,)为与控制点有关的二维张量积NURBS基函数;为控制点处壳体中面的法向量,=[,1,2,3],采用Greville横标点计算。
基于等参概念,采用与几何场相同的插值函数,壳的位移表示为
(,,)=

(2)

对于阶基函数,完全积分需要+1个高斯点。位移场与转动场不一致会导致剪切闭锁,因此使用个高斯点的减缩积分方案避免这一问题。
通过最小位能原理,最终得到等几何R-M壳单元的刚度矩阵
=∭d=
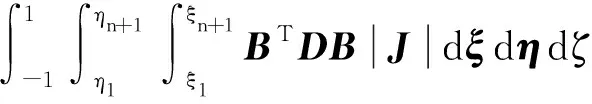
(3)
在图1中给定一点,其坐标为(,,),根据式(2),点的速度可以通过点计算得到,即
=+
(4)
其中:

(5)
点处体积微元的动能为

(6)
根据直法线假设,点相对于点的位置表示为=[0 0]。将式(4)代入式(6),得到采用中面表示的动能方程,即

(7)
式中:为材料密度;

(8)

(9)
采用等几何形函数进行离散,对式(7)在单元域上进行积分,得到一致质量矩阵,即


(10)
1.2 适用于R-M壳的微梁键
近场动力学是一种使用积分方程求解连续和非连续场的理论。该理论假设粒子与周围一定距离范围内的其他粒子存在相互作用,损伤发生在粒子水平上。参考构型中2个粒子的相对位置为
=′-
(11)
相对位移为
=(′,)-(,)
(12)
这2个相互作用的粒子之间形成PD键。粒子作用在粒子上的力可由微势能求导得到,即

(13)
微势能是单根键上的能量,其单位是单位体积的平方,所以给定点的单位体积的能量即局部应变能密度

(14)
系数12是指每根键的每个端点上只有键上12的能量。基于近场动力学理论的微梁键,将PD键视为类似于经典Timoshenko梁模型,承受轴向变形、扭转变形、弯曲变形和横向剪切变形,称之为微梁键,见图2。

图 2 PD微梁键示意
每个微梁键的端点有3个平动自由度(,,)和3个转动自由度(,,),通过插值方式可获得键的变形。键在局部坐标系下的位移向量为

(15)
根据文献[14-15],为描述壳结构的变形,微梁键上一点的变形可以分成面内变形和横向变形两部分,即
,Shell=,PlaneShell+,TranShell
(16)
面内变形微势能由端点平动产生的轴向变形能和端点转动产生的横向变形能组成,则

(17)
式中:a,为键在拉伸和压缩作用下的微模量;b,为与面内弯曲相关的微模量;为键的长度。
由壳横向变形相关的微势能可得

(18)
式中:为与转动相关的微模量;b,和s,分别为由于键绕轴转动产生的与弯曲和横向剪切相关的微模量。
根据应变能密度守恒原理,微梁键基壳模型的应变能密度必须与弹性壳理论的应变能密度相等。通过插值离散微梁键模型,得到微模量的表达式为

(19)
最终,局部坐标系下微梁键的力密度与位移的关系表示为
=
(20)

(21)

(22)
的具体细节可参阅文献[14-15]。
2 非连续伽辽金PD壳
在经典PD模型中,物理域被离散成粒子,称为无网格PD离散方法;近几年发展的另一种方法是将模型域离散成单元,再应用DG方程。例如,REN等使用DG模型离散裂纹存在的非局部模型,使用有限元法离散连续模型域。与粒子法相比,DG方法可以在计算域内使用更高精度的积分,可以更方便地计算应力和应变场。采用微梁键基PD壳模型计算的系统总能量为

(23)


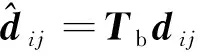
(24)
式中:为全局坐标系下点和的位移;为全局坐标系到键局部坐标系下的旋转矩阵。
使用DG方法时,需要先将模型离散成单元,本文采用由控制网形成的4节点单元,见图3。为所有单元的共享节点插入新的节点,解除单元之间的节点关联。这种单元的拆分过程可保证各个单元的独立性,使裂纹扩展分析可以顺利进行。
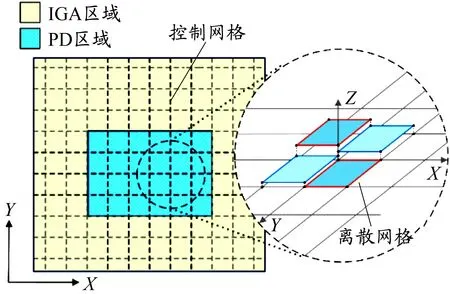
图 3 DG离散中的单元拆分示意
在PD壳的DG法中,单元是计算模型的基本组成部分。在列式中,单元的高斯点被视为PD节点,见图4。

图 4 DG单元的高斯点之间形成PD键
单元的高斯点被视为附着在单元上的PD节点。两单元的任意2个高斯点之间形成键,如图中键连接点和点,点的近场域由单元决定。单元中的4个PD点都采用单元形心形成的近场域,单元和单元之间的关联通过键的相互作用建立,即

(25)

令和分别表示单元坐标系与全局坐标系之间位移向量的转换矩阵,则

(26)
将式(24)~(26)代入式(23),得


(27)
采用DG法的单元与单元之间的单刚矩阵可写为
=

(28)
对所有单元的刚度矩阵进行累加,即得到结构的整体刚度矩阵。
3 基于力/力矩平衡原理的耦合模型
DG列式方法增加单元节点的数量,因此降低计算效率。为提高裂纹扩展仿真的计算效率,根据前文获得的IGA壳模型和DG壳的PD模型,采用非局部模型和经典连续介质力学模型耦合的方法,得到壳结构的动力学平衡方程,即

(29)
方程的每一行表示一个自由度所处的一种力力矩平衡状态。处于一种边界条件下的结构,其所承受的等效载荷向量相等,即满足=。当采用IGA模型或PD模型求解时,2种模型得到的位移解应该相同,即满足=。因此,方程又可表示为

(30)
根据式(30),可提出基于力力矩平衡的耦合求解方法。将计算域按等几何控制点形成的网格划分为IGA域与PD域,见图5。

图 5 耦合模型示意
由此,耦合刚度矩阵可表示为

(-())+()
(31)
式中:为对角矩阵,
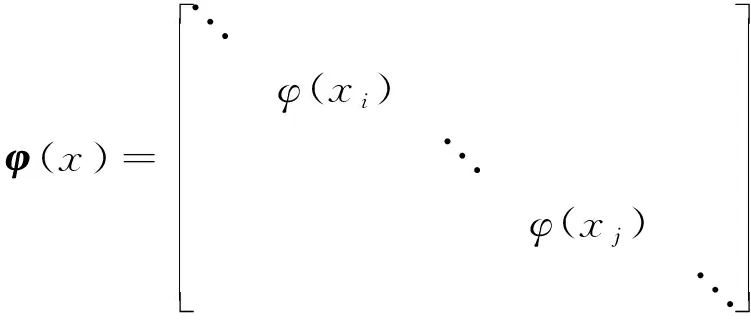
(32)
且满足

(33)
耦合后的动力学平衡方程表示为

(34)
由式(30)可以清楚地看出,式(34)中的每个方程都成立。节点各自由度对应的力和力矩状态是平衡的,因此这种方法称为力力矩平衡耦合方法。
对于线弹性静力学问题,可以通过求解线性方程获得模型的位移解,即
=
(35)
对于裂纹动态扩展问题,可采用中心差分法求解。系统待求解的运动方程为

(36)

4 算 例
4.1 带初始裂纹板的裂纹扩展
本算例被广泛用于评估裂纹扩展仿真算法的准确性。初始裂纹板模型及PD区域设置见图6,板的材料参数为=72 GPa,=033,=2 440 kg/m,=135 J/m;作用在模型上下边界的均布载荷为=12 MPa;将近场域大小设置为=3Δ。

图 6 初始裂纹板模型,mm
计算得到不同时间步下的裂纹扩展路径,见图7。IGA-PD耦合模型模拟壳裂纹扩展是有效的。同时,根据裂纹扩展区域的分布,可选择合适的区域作为PD区。对于裂纹扩展区域分布集中的问题,可以采用IGA-PD耦合算法提高裂纹扩展分析的计算效率。

图 7 初始裂纹板的裂纹扩展路径
4.2 平行预置裂纹板的裂纹扩展
为检验耦合算法在复杂裂纹条件下对裂纹扩展和合并的仿真能力,采用受位移载荷的预置平行裂纹板算例,见图8。考虑裂纹角度=0和=45°这2种情况,几何参数=10 mm,=10 mm。模型参数=30 GPa,=033,=2 700 kg/m,=30 J/m;将近场域大小设置为=3Δ。模型上下边界给定0.04 mm位移,分2 000步线性加载,时间步长Δ=5×10s,则位移加载速度为0.4 m/s。PD区域根据预制裂纹分布进行布置。对于图8中的倾斜裂纹,可设置包围裂纹的区域为PD区域。裂纹扩展过程见图9和10。2种角度的裂纹均在开始阶段各自生长,内侧相互靠近并逐渐合二为一,外侧向两侧扩展至边缘。裂纹扩展路径与文献[23]中的结果一致。

图 8 平行预置裂纹板模型,mm

图 9 α=0°平行裂纹板的裂纹扩展路径

图 10 α=45°平行裂纹板的裂纹扩展路径
采用=0的模型研究不同PD区域大小对计算效率的影响。所用测试设备参数为CPU Intel i5-7400 3.00 GHz,RAM 32 GB 2 400 MHz,硬盘TOSHIBA DT01ACA100 7200 HDD 1 TB。以划定的PD区域面积占整个模型总面积的比例为横坐标,以采用耦合模型求解时间与采用纯PD模型计算时间的比值为纵坐标,不同PD区域占比的计算时间与纯PD区域的计算时间的相对用时对比见图11。由此可知,随着PD区域所占比例的增加,计算时间也增加。采用20%区域为PD区域,其余区域为IGA模型区域时,所需计算时间为纯PD模型的25%,说明与PD方法相比,使用IGA-PD耦合方法能够提高计算效率。

图 11 不同PD区域时的计算时间对比
4.3 受内压的圆柱壳
为检验耦合算法在一般壳结构断裂仿真方面的性能,采用圆柱作为研究对象,模拟其在受内部压强作用下的断裂过程。带预制裂纹的受内压圆柱壳模型见图12。材料参数=70 GPa,=03,=1.5 J/m;模型承受的内部压强=1 MPa;设置近场域大小为=3Δ。

图 12 带预制裂纹的受内压圆柱壳模型,mm
根据模型的对称性,采用1/2几何模型,轴向设置为67个控制点,周向设置35个控制点,得到2阶张量积B样条曲面。圆柱模型的裂纹扩展路径见图13。裂纹沿着与预置裂纹方向一致的方向扩展,并自始至终沿着与轴线平行的方向向两侧传播。在一般壳结构中,所提出的耦合算法在精确几何表示和断裂仿真方面的性能均较好。

图 13 圆柱模型的裂纹扩展路径
5 结束语
针对壳结构中的裂纹扩展问题,建立等几何分析(IGA)与近场动力学(PD)耦合的分析模型IGA-PD。在计算过程中,将模型域划分为IGA域与PD域。IGA域采用基于Reissner-Mindlin(R-M)理论的退化壳模型,考虑横向剪切的影响,保证几何精确性,避免传统有限元离散引入的几何误差,在法向向量计算等方面更加准确。PD域采用基于微梁键的非连续伽辽金(DG)有限元壳模型,实现对非连续场的计算分析。耦合过程基于力/力矩平衡原理,将等几何刚度矩阵与近场动力学刚度矩阵耦合。数值试验结果表明,该耦合模型可高效模拟板壳结构中的裂纹扩展,准确计算裂纹的开裂和交叉等现象。与PD模型相比,本文方法可有效提高计算效率,对于裂纹扩展区域相对集中的问题,可将计算时间缩短至原耗时的25%。

