图像边缘特征检测实现多目标跟踪的有序匹配算法研究
王 琪
(江苏联合职业技术学院扬州分院继续教育部 江苏扬州 225003)
0 引言
在视频车辆检测方面,单一的特征计算相对简单高效,对高速公路这类简单环境情况下的目标检测具有较好效果。但其实用性不强,对噪声干扰较为敏感,特别在有行道树、云彩、行人天桥、建筑物等相似干扰目标出现时,误检率迅速增加。对于解决城区复杂交通场景下的目标检测问题,单靠某一种特征计算很难完成检测任务,每种特征计算都有一定的适用范围,多特征组合方法是当前主流[1]。另外,基于先验知识的特征计算很容易受到环境噪声干扰,适应性差。区域统计特征计算由于具有相对稳定、鲁棒性强、抗干扰能力强等优点,已成为当前目标检测的热点。
1 特征提取
特征提取在图像处理研究中具有重要的地位,众多学者对特征提取的方法进行了大量的研究。特征提取的种类不仅是对形状特征的提取,还有对颜色特征、空间特征的提取。在目前的形状特征提取研究中,有两种表示方法:一种是以图像轮廓或边界进行特征提取,另一种是对图像所在区域进行特征提取[2]。前者目标是图像的边界,后者目标是图像的整个区域。以下是比较常见的特征提取方法:
1) 边界描述特征法。基于Hough的边界特征法的基本思想主要是通过对边缘特征的描述获取图像的基本形状参数。Hough是利用图像的区域特性将边缘组成一种封闭的区域边界,其基本思想是将集中的点连成线。边界直方图的基本思想是求出图像的边缘,然后做出有关于边缘方向的直方图。
2) 几何法。将形状的表达方式变为数学的几何表达方式。每个图像都有周长和面积等几何参数。
3) 区域参数法。每一个实物都有其区域,而这个方法就是将实物区域作为不变量来描述形状。
为了更好地解决在城市复杂环境下的车载多目标检测问题,本文通过对特征的选择对比分析发现,统计特征以及组合特征均能在复杂环境下具有较好的鲁棒性。本文选择提取车辆外框以及人的头肩等区域信息,这些区域均具有明显的固定边缘和线性特征,这也是本文检测的目标区别于其他目标(如:桥梁、树等非规则目标)较为显著之处。在此基础上,提出采用Harr与HOG组合特征的两步目标检测算法。Harr特征能够很好地表达目标边缘和线性,尽管该特征比较粗略,但通过AdaBoost级联分类器,可以舍弃那些大量的且对检测不起作用的特征,而保留少量的对目标检测起关键作用的特征,因此检测效率很高[3]。
2 有序匹配算法
现有特征匹配的图像检测方法中,一般都是特征间的一对一匹配,一组匹配特征间是独立匹配的,不考虑所选取的目标图像描述特征间的逻辑关系与结构等,这就使得匹配结果通常表现出局部性,难以从全局上实现目标图像的准确检测[4]。因此,本文提出一种基于图同构理论的特征匹配方法,综合编辑距离、层次关系等特征,计算目标特征的结构级相似性,对目标图像特征的表示有向图中以点、边有序交替匹配的方式来判断目标的有向图近似同构,从而实现基于子图同构判定的目标图像检测。
以上特征匹配思想的基础是图匹配问题,其本质上是一个NP完全问题,这类问题的常用解决方案是通过计算和匹配结构的相似性实现,其指导思想是:基于相邻元素相似性倒推元素自身相似度,即,若节点的邻居节点相似,则节点本身也相似,其核心是相似度传播算法。最典型的两个基于结构的本体匹配算法SF和GMO,其核心思想都是:拥有相似父/子概念的概念可能相似,拥有相似属性的概念可能相似。
基于子图近似同构的特征匹配方法(Charactore Matching based Subgraph Isomorphism, SICM)框架如图1所示。由图1可知,SICM是一个顺序匹配器,主要包括4个主要功能模型:锚点与子图提取、结构相似度量、子图近似同构判定、基于子图同构的目标匹配。
所谓锚点,是指待目标中第一对确定为相似的属性特征,表现在有向标记图中就是第一对确定匹配的节点,其形式化定义如下:
2.1 定义1
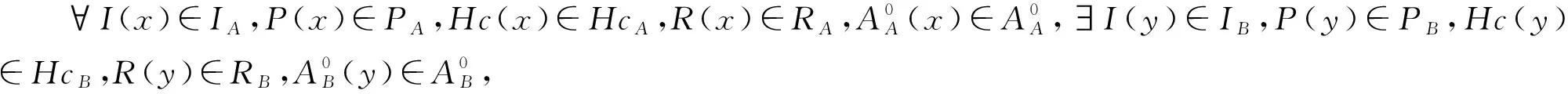
对于待匹配目标的特征双重编码A和B,计算其对应的有向图G(A)和G(B)的相似度需要完成如下计算:① 特征编辑距离相似度;② 特征层次关系相似度;③ 特征其他关系相似度;④ 结构相似度。具体解释如下:
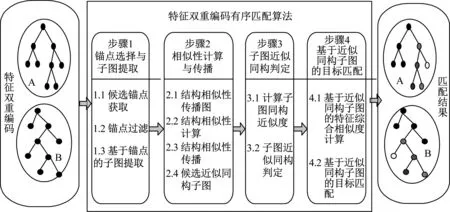
图1 特征双重编码有序匹配算法框架
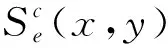
(1)
则x与y间编辑距离相似度计算如式(2):
(2)
其中,α、β为权重调整参数,且0<α,β≤1∧α+β=1。
2) 特征层次关系相似度:设x在G(A)中入度集为xin={xi∈V(A)|∃xiHcx},出度集为xout={xj∈V(A)|∃xHcxj},类似y在G(B)中入(出)度集分别为yin、yout,则x与y层次关系相似性计算如式(3):
(3)
xin⟺yin={x|x∈xin,y∈yin:Se(x,y)∈OM(x,y)}表示x、y父节点中可匹配的节点集;
xout⟺yout={x|x∈xout,y∈yout:Se(x,y)∈OM(x,y)}表示x、y子节点中可匹配的节点集。
3) 节点间其他关系相似性:记与x、y存有R关系的节点集合分别为xR={x′∈V(A)|r∈RA:∃(x′rx)∨(xrx′)}和yR={y′∈V(B)|r∈RB:∃(y′ry)∨(yry′)},若∃r1∈RA,r2∈RB,有式(4)成立:

(4)
则记节点集为xR⟺yR,以加权后得到节点间其他关系相似度计算如式(5):
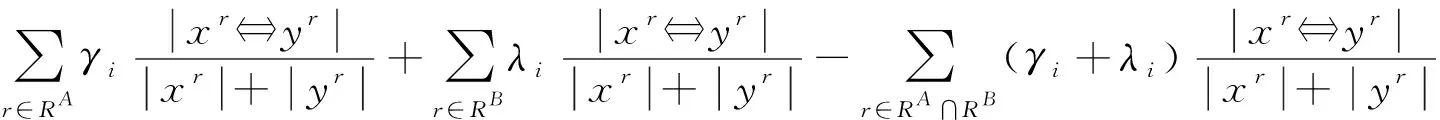
(5)

4) 结构相似性:设
S(G(x),G(y))=η·Se(x,y)+φ·SHc(x,y)+ξ·SR(x,y)
(6)
η+φ+ξ=1为权重参数。
若两个有向图G、G′点、边间保持一一对应关系,且对应点(边)间保持相同关联关系,则G和G′同构,记为G≅G′。
由于图像检测中只需关键特征的相似度满足阈值要求即可判定为匹配,因此本文提出了图的近似同构概念。
2.2 定义2
设给定目标A和B,其有向图分别为G(A)和G(B),若根节点a∈G(A),在G(B)中存在一点b,有
基于图近似同构,SICM算法思想是:按广度优先遍历法,在确定匹配锚点后,基于节点出入度进行节点与边的有序交替匹配,直至在G(B)中找到一个与G(A)近似同构的子图。算法的主要步骤是:①在G(B)中找到根节点a∈G(A)的锚点b;②生成锚点导出有向图G(Bb);③判定G(A)与G(Bb)是否满足图近似同构。若满足则认为其是可匹配的,否则,迭代上述过程直至收敛。
3 图像边缘特征检测
所谓边缘特征检测,就是计算图像中像素亮度变化差别很大的点的导数,应用求导方法检测数字图像的灰度值不连续的现象[5]。如图2所示。
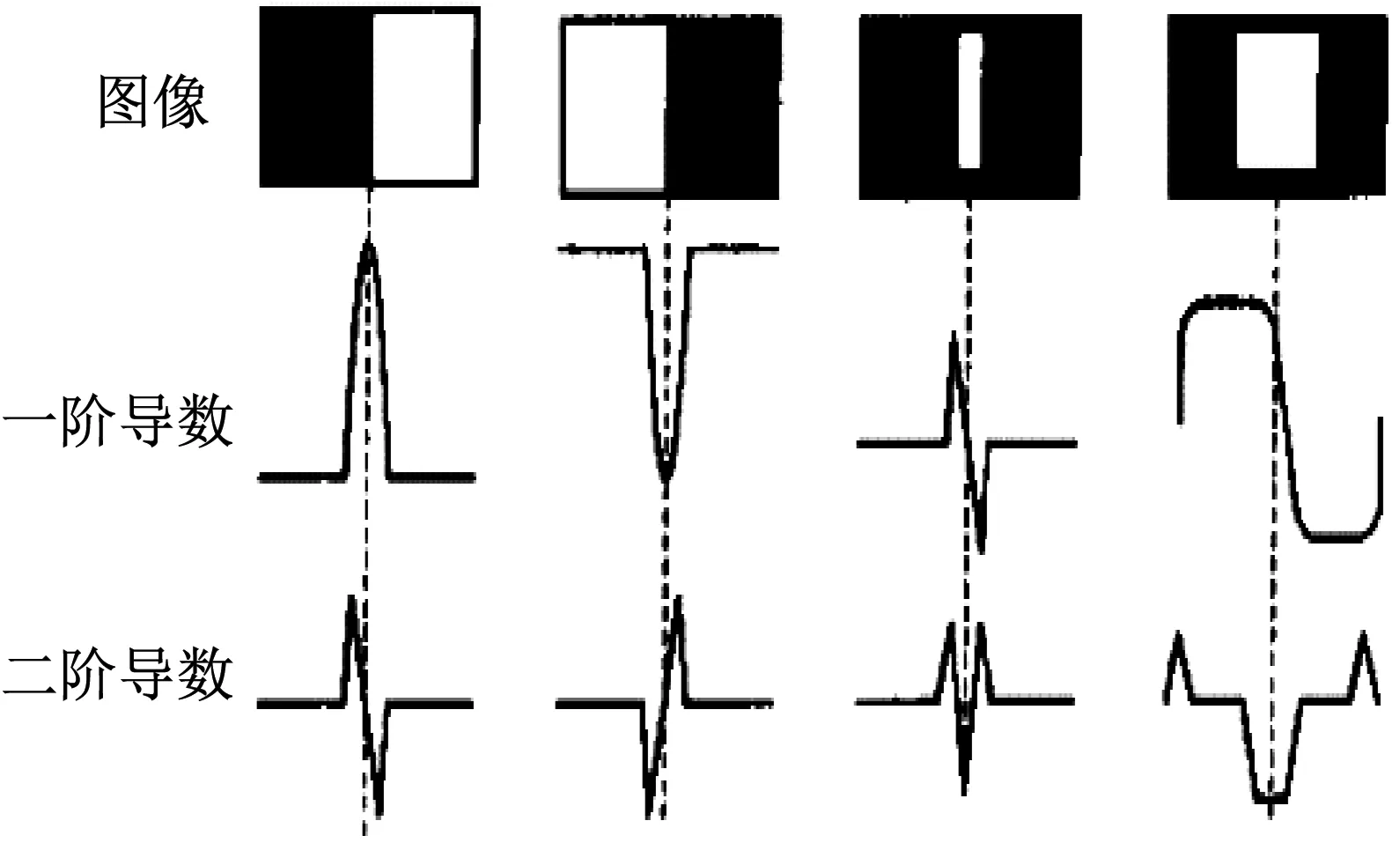
图2 图像边缘及相应导数
3.1 梯度算子
梯度和一阶导数相对应,相应梯度算子就对应相应的一阶导数算子,等式是一个连续函数f(x,y)在(x,y)处的梯度计算:
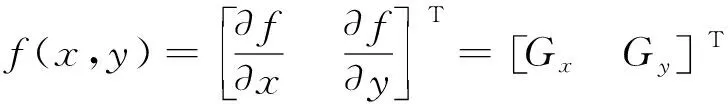
(7)
梯度是一个矢量,存在幅值和相位,相位和幅值分别如下:
(8)
(9)
3.2 Laplacian算子
Laplacian算子是一种应用于二阶导数的算子,一个连续函数f(x,y)在(x,y)处定义如下:
(10)
Laplacian算子在图像处理中也需要利用模板实现,且模板有两个特别之处;第一是在模板的中心处该系数必须为正数;第二是模板内的所有系数之和为零。
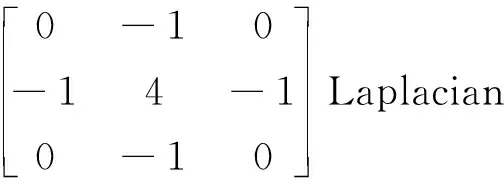
(11)
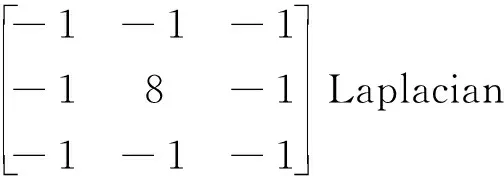
(12)
拉普拉斯算子检测图像的边缘,经常会产生有双像素的边界,此外对噪声也比较敏感,所以一般不会使用这种方法对图像边缘检测。
4 有序匹配算法的图像边缘特征检测
4.1 Prewitt算子
Prewitt算子是一种对像素点在该领域内各个方向上的像素差,并且在图像的像素边缘出现的极大值或极小值判断边缘,从而确定边缘,消除不确定的边缘,平滑噪声的效果明显。检测的具体方向模块各自检测相应的对象,一个检测水平方向边缘,另外一个则是检测垂直方向的边缘,方向模块如表1所示。

表1 Prewitt算子方向模块
一个连续的函数f(x,y),应用Prewitt算子算法,得到以下数学公式:
Gx=|[f(x-1,y-1)+f(x-1,y)+f(x-1,y+1)]-
[f(x+1,y-1)+f(x+1,y)+f(x+1,y+1)]|
Gy=|[f(x-1,y+1)+f(x,y+1)+f(x+1,y+1)]-
[f(x-1,y-1)+f(x,y-1)+f(x+1,y-1)]|
(13)
则p(x,y)=Gx+Gy
(14)
若P(x,y)大于或等于阈值T,则(x,y)表示边缘处的像素点,P(x,y)则表示为边缘图像,但是,应用这种方法检测图像边缘,会存在一个问题,错误判断图像的边缘,因为有些噪声点的灰度值很高,或者本来应该有的边缘点因为其灰度值比较低,在检测边缘时没能正确检测出来,导致出现多余的边缘或者丢失了图像的某些边缘。
对于灰度值较低的图像边缘,使其灰度值增加,可以对图像进行锐化,然后再Prewitt算子边缘检测,图像锐化的效果就是使图像灰度的反差增强,把模糊的图像变得更加清楚,增加其对比性,这里选择拉普拉斯算子的方法具有很好的锐化效果,能够增强图像灰度突变区。这种方法既能保留原图像的灰度值,还能突出图像的细节信息。拉普拉斯锐化方程如式(15):
(15)
应用Prewitt算子图像边缘检测源程序如下:
I = imread(检测图像);
J1= edge(I,′prewitt′,0.04);0.04%为梯度阈值
Figure,imshow(I);
Figure,imshow(J1);
4.2 Log算子
Log算子是一种结合高斯滤波和拉普拉斯算子两种算子的方法对图像进行边缘检测,Log算子边缘检测方程式如下:
∇2g(x,y)=∇2[h(x,y)×f(x,y)]=
∇2h(x,y)×f(x,y)
(16)
σ等于2的Log算子检测图像的边缘,检测结果如图3,其源程序如下:
I = imread(检测图像);
BW1 = edge(I,′log′,0.003); % σ=2
imshow(BW1);title(′σ=2′)
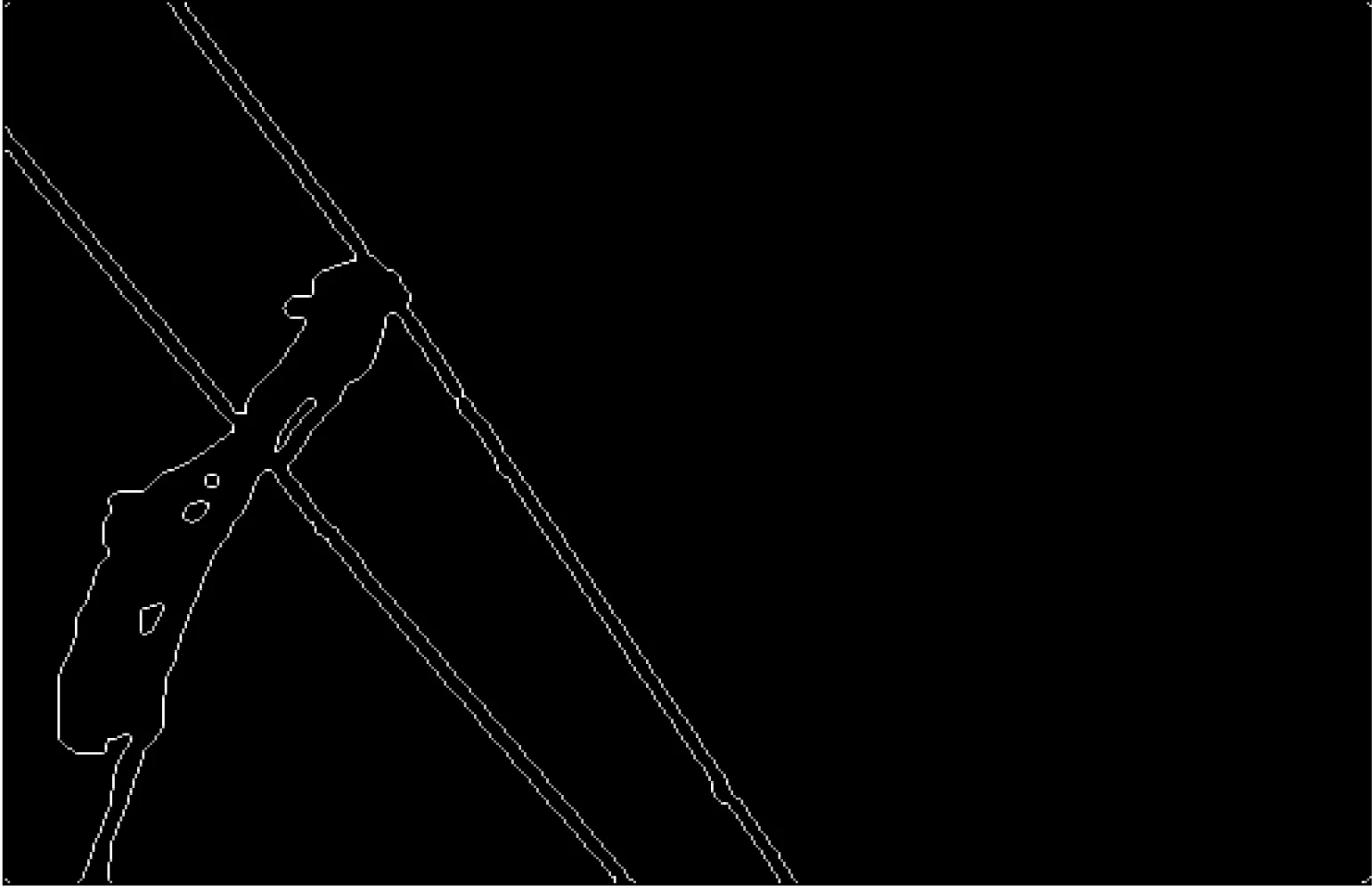
图3 Log算子图像边缘检测
4.3 Canny算子
Canny算子是使用双阈值法检测边缘,这两个阈值有不同的用法,其优势在于不易受噪声影响,能检测出图像真正的弱边缘,提升边缘敏感度,检测性能较好。边缘检测源程序如下:
I = imread(检测图像);
imshow(I);
BW1 = edge(I,′canny′,0.2);
Figure,imshow(BW1);
Canny算子检测效果如图4。
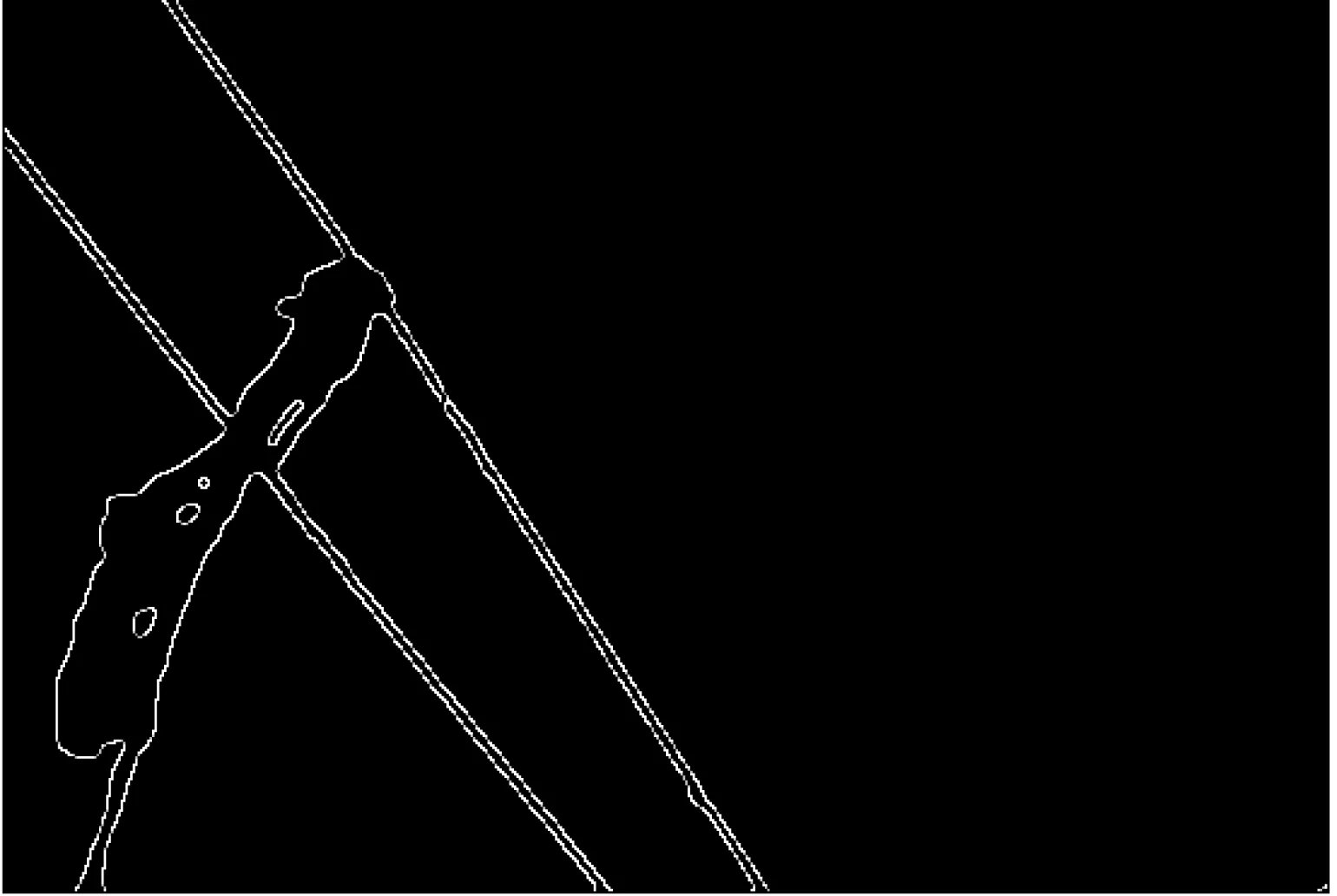
图4 Canny算子检结果图
5 有序匹配算法的多目标跟踪
5.1 道路背景提取
在系统调试测试过程中,道路背景提取是其基础,以下说明这个测试过程中遇到的几个典型问题及其解决办法:① 车辆在没有停车标志的路段进行倒库处理。用串口给上位机发送此处的图像,将图像和识别停车标志P的程序进行比对,发现该处算法存在漏洞,经多次改进后让车辆实现只在有停车标志的路段进行停车处理。② 程序没有改动但车辆行驶行为识别效果完全不一样。经调研分析后发现,电池供电不足会导致这种现象。③ 无端客户端出现系统安装包突然无法下载现象。查阅K60的相关资料后可知,是由于插拔下载器不当导致K60进行自锁保护,对其进行解锁即可继续使用。
5.2 常规道路检测
图5是车辆行驶在双车道的左车道时的情况,其中有几行的中心线略偏右,从图5中可以看出中心线略偏右的那几行没有右边界,这种情况下程序中先预估右边界值,然后中心值取左右边界值之和的一半,由图5可看出调试结果和程序设定的一致,拟合出的中心线近似一条直线且在图像的中间。

图5 双车道路段
图6是车辆行驶在单车道时的情况。图6和图7虽然都是车辆在直道处的情况,但在程序上是分别处理的。因为单车道的情况是所有路况中最容易判别的,双车道的情况容易和过弯混淆。由图7可以看出单车道路段处程序拟合出的中心线在图像的中间位置且近似直线,所以本文针对此类路段设计的算法是正确的。

图6 单车道路段
图7是车辆行驶到有行驶方向指示路口时的情况,在这种情况下,中心线的拟合要稍作调整,否则容易出现箭头所在行的中心值偏右的情况,这是因为箭头处也有黑白跳变的明显特征,从而导致查找道路左边界时发生误判。由图7可知,中心线拟合正确,没有出现各行中心值差别很大的情况。
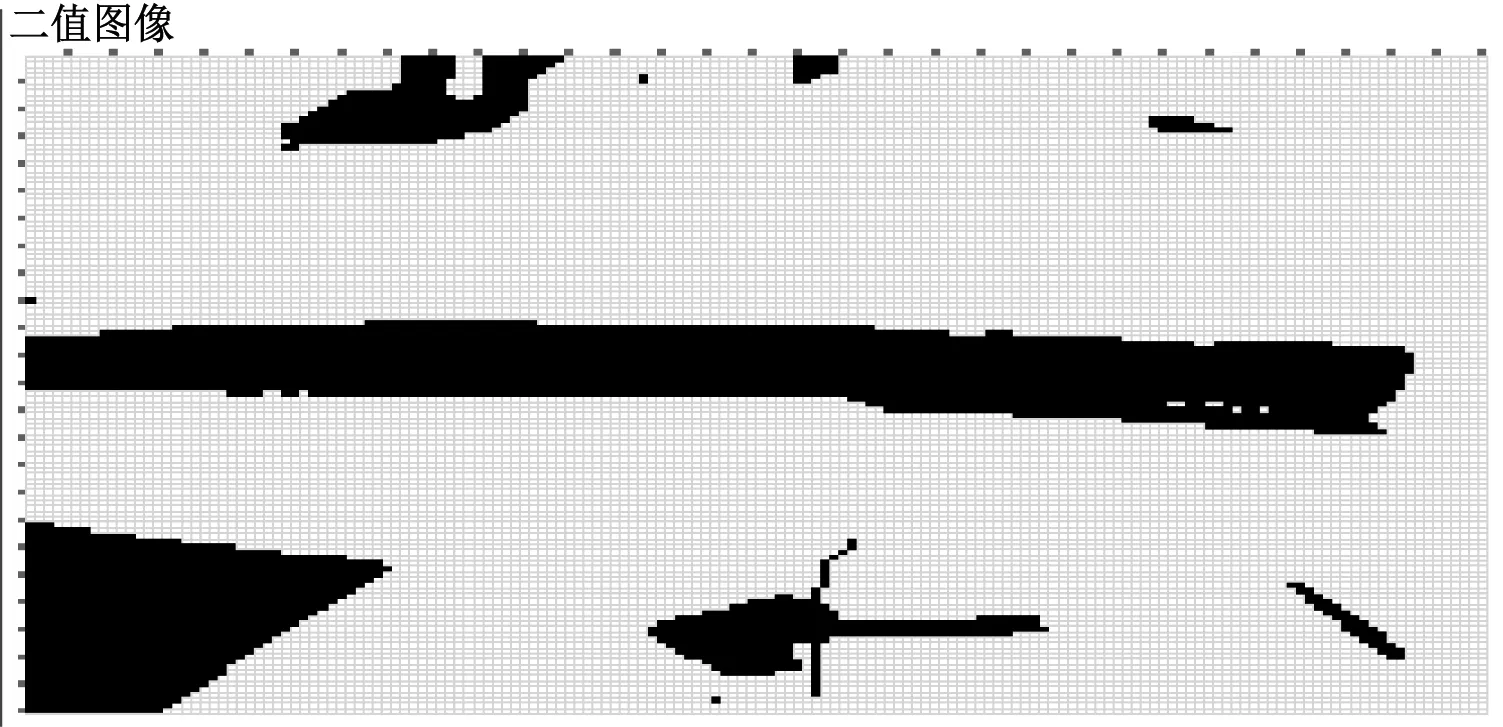
图7 有行驶方向指示的路口
图8和图9是车辆进弯道前和进弯道后的情况(以左拐为例)。车辆进入弯道前,可以采集到道路两边边界值,通过计算左右边界值的平均值即可得到中心线。车辆进入弯道后,左侧边界值无法找到,这种情况下每行的中心值是按如下方法计算得到。现设A为任一行的中心值,B为该行右边界的边界值,C为该行的上一行的中心值,D为上一行的右边界值,则A=C+(D-B),由图10所示,拟合出的中心线和右边界变化趋势一致,所以拟合出的中心线正确。
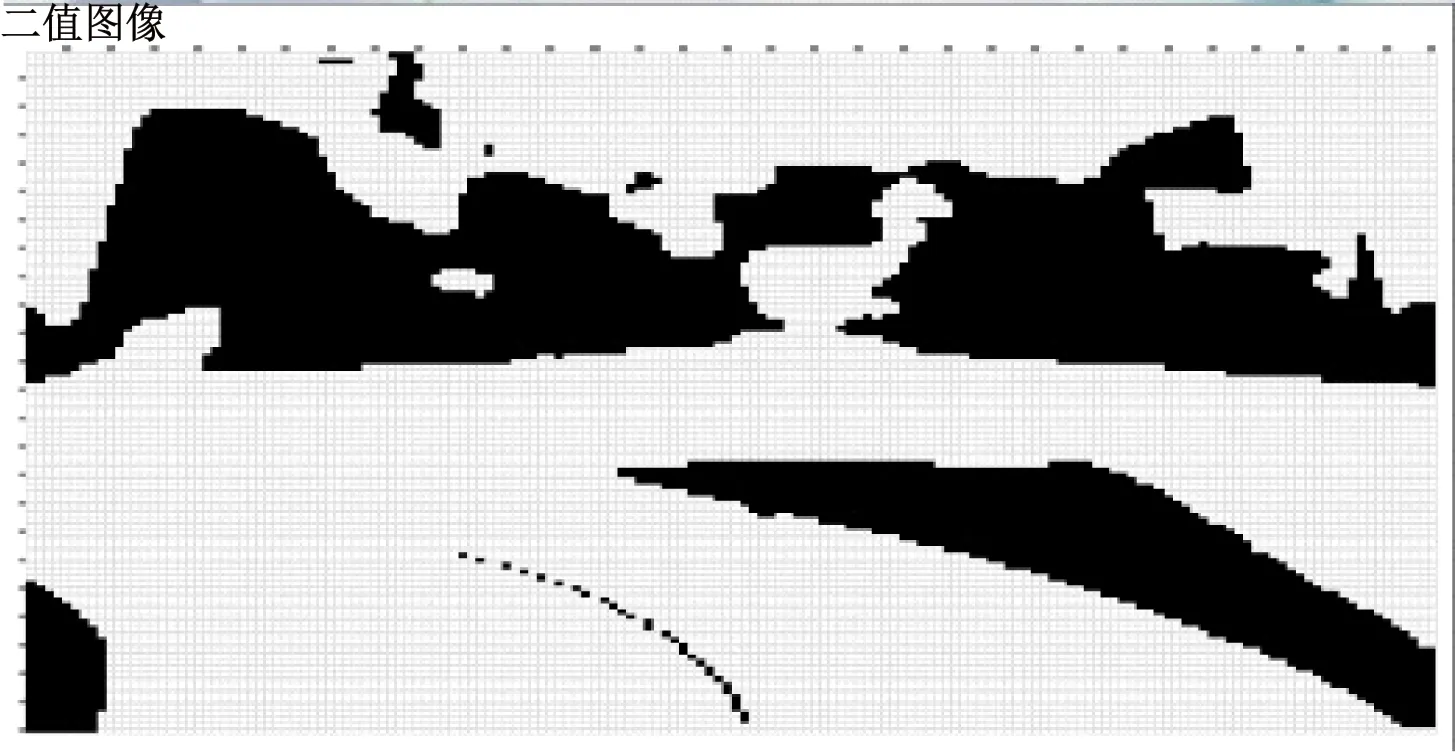
图8 进入弯道前的中心拟合线

图9 进入弯道后的中心拟合线
5.3 有交通灯路口处的车辆识别
图10是车辆在十字路口判别到有交通灯情况下的识别图,由图10右边的标志位turn_left=1可以看出,程序在处理这幅图像时识别到了左转的箭头,所以本文设计的交通灯识别算法可行。

图10 交通灯路段
5.4 特殊交通标志检测识别
图11为车辆到达可停车路段时的情况,由图11右边的标志位Find_p=1(最后一行)可以看出,图像经过识别处理后找到了停车标志P,所以本文设计的停车标志识别算法可行。

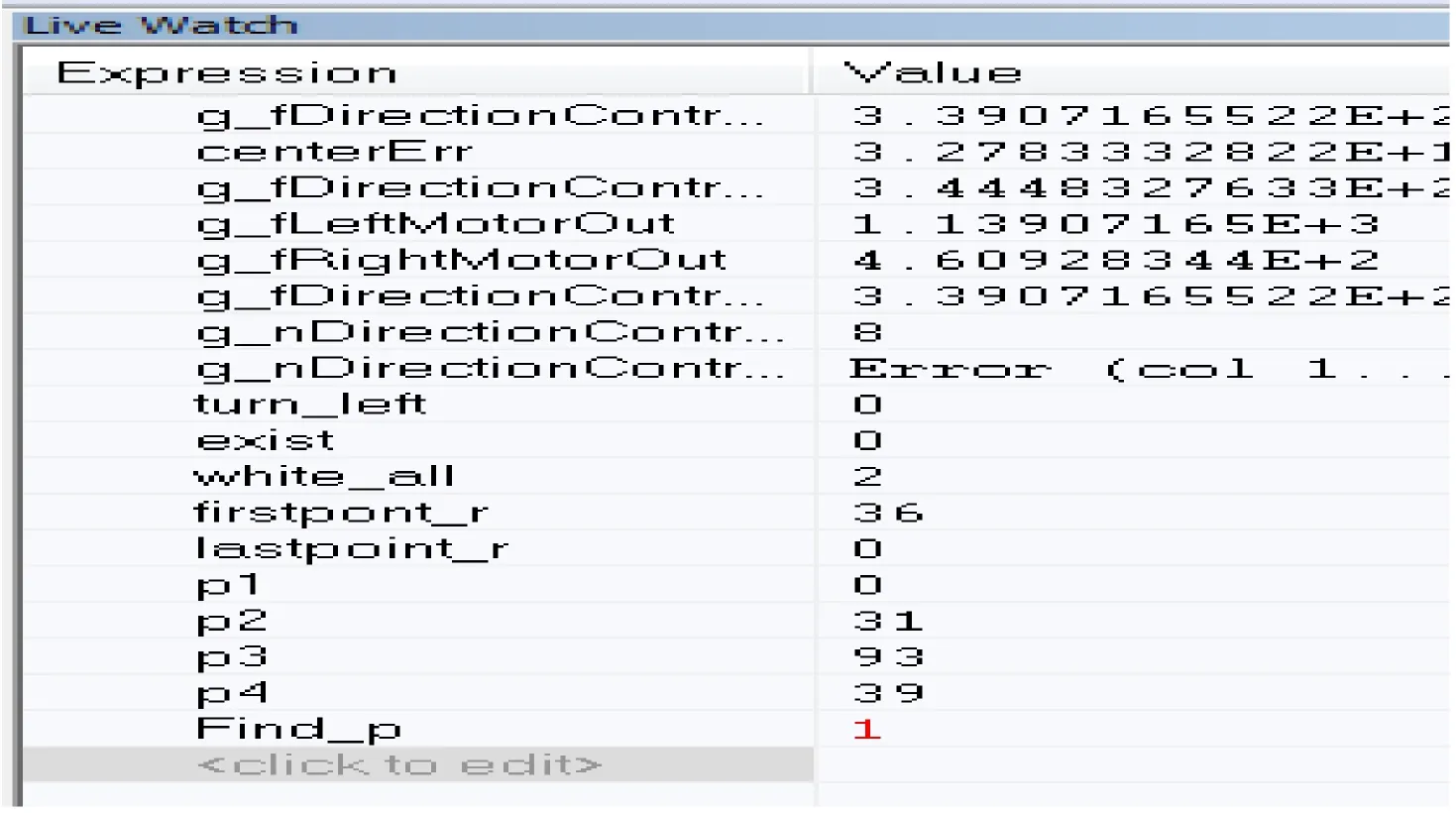
图11 可停车路段
图12是车辆遇到障碍时的情况。由图12可看出中心线较平滑,没有分成明显的两段式,这说明小车在此处识别到障碍,中心线得到了平滑处理,所以可以得出障碍识别算法正确。平滑的中心线会让小车在进障碍和出障碍时行驶得较流畅,不会产生迟钝现象。

图12 障碍路段
由于设置的道路情况较多,识别的工作量大,导致难度也很大,调试的过程经常出现误判,程序进行了多次的BUG修改,经过多次调试最终得到了以上这些效果图。
6 结束语
基于特征匹配的方法提取目标几何特征,将特征输入预测模型,通过预测模型求解出下一帧中目标可能出现的位置或运动状态,构造不同的特征相似性度量函数,使相邻帧间的目标可以匹配,实现多目标跟踪[6]。Prewitt算子、Log算子、Canny算子是实现多目标跟踪的典型算法,多层级联检测有助于提高复杂环境下多目标检测的准确度,通过对直方图距离函数最小化来追踪目标,发挥计算量小、适应性强的优点。未来,可进一步获得距离、方位、速度等参数,更好地检测图像边缘特征,实现多目标跟踪。

